Hough Transform 1 Hough Transform A Technique to

Hough Transform 1

Hough Transform A Technique to Isolate Features of a Particular Shape within an Image The classical Hough transform is most commonly used for the detection of regular curves such as: lines, circles, ellipses, etc Because: The desired features be specified in some parametric form 2

Voting schemes Let each feature vote for all the models that are compatible with it Hopefully the noise features will not vote consistently for any single model Missing data doesn’t matter as long as there are enough features remaining to agree on a good model 3

Properties Can tolerate noise and gaps in edge image Look for solutions in a parameter space Classical Hough transform Detect simple shape Line detection Circle detection 4

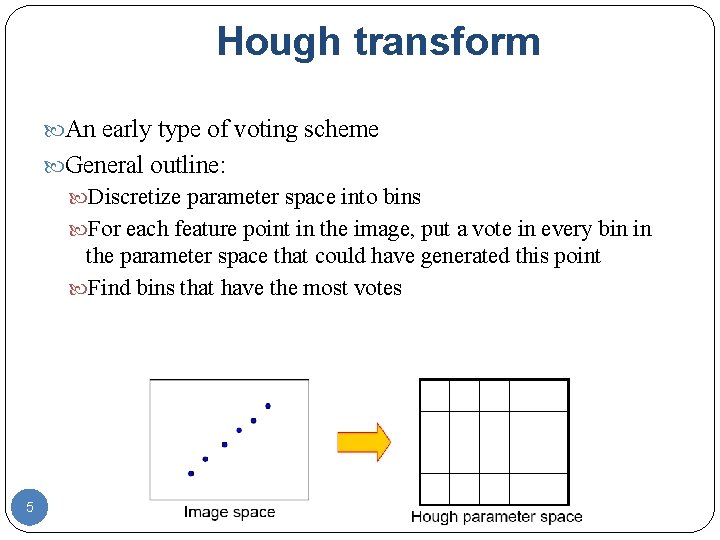
Hough transform An early type of voting scheme General outline: Discretize parameter space into bins For each feature point in the image, put a vote in every bin in the parameter space that could have generated this point Find bins that have the most votes 5

Hough Transform • Instead of going directly for the solution (as in template matching), we can use a voting scheme. • Each possible point (edge) votes in the parameter space of a line. • A line can be specified uniquely by two parameters m and n. y = m. x + n • Parameter space of 2 dimensions (m and n). 6 ﺷﻨﺒﻪ ﺯﺍﺩﻩ

Finding lines in an image y b b 0 x image space m 0 m Hough space A line in the image corresponds to a point in Hough space Connection between image (x, y) and Hough (m, b) spaces • A line in the image corresponds to a point in Hough space • To go from image space to Hough space: - given a set of points (x, y), find all (m, b) such that y = mx + b 7

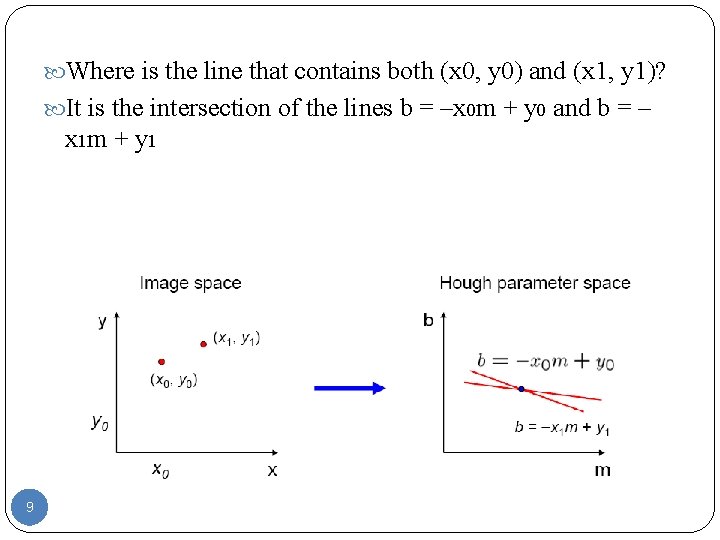
Where is the line that contains both (x 0, y 0) and (x 1, y 1)? 8

Where is the line that contains both (x 0, y 0) and (x 1, y 1)? It is the intersection of the lines b = –x 0 m + y 0 and b = – x 1 m + y 1 9

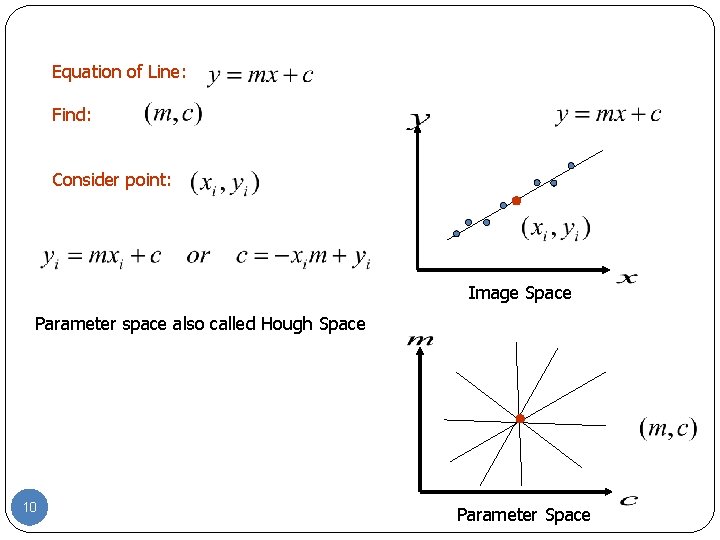
Equation of Line: Find: Consider point: Image Space Parameter space also called Hough Space 10 Parameter Space

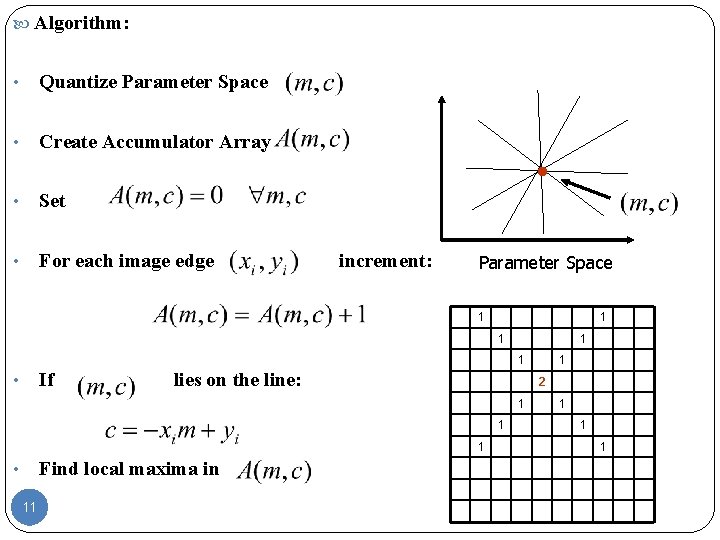
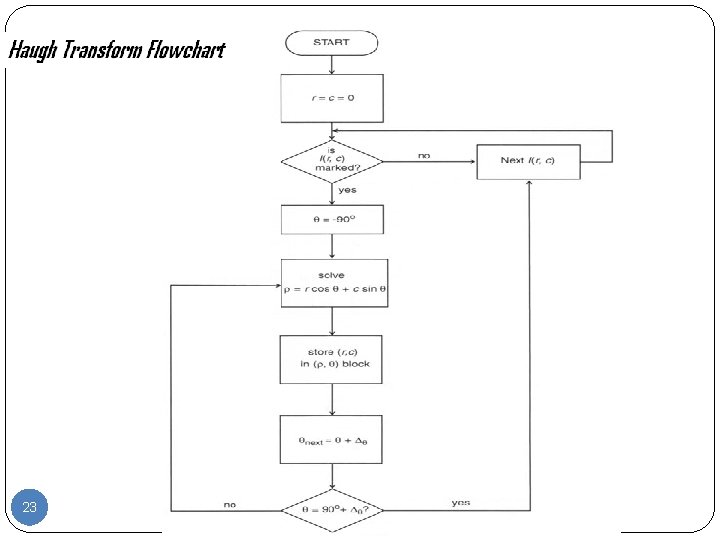
Algorithm: • Quantize Parameter Space • Create Accumulator Array • Set • For each image edge increment: Parameter Space 1 1 1 If • lies on the line: 2 1 1 1 Find local maxima in • 11 1 1

Problem with m-n parameter space. Both m and n can get very large [-∞, ∞]. How do we address this problem? 12 ﺷﻨﺒﻪ ﺯﺍﺩﻩ

An alternative parameter space is polar coordinates. We use (ρ, θ) space to represent a line. ρ = x. cos(θ) + y. sin(θ) Points in picture sinusoids in parameter space Points in parameter space lines in picture Sinusoids corresponding to co-linear points intersect at an unique point 13

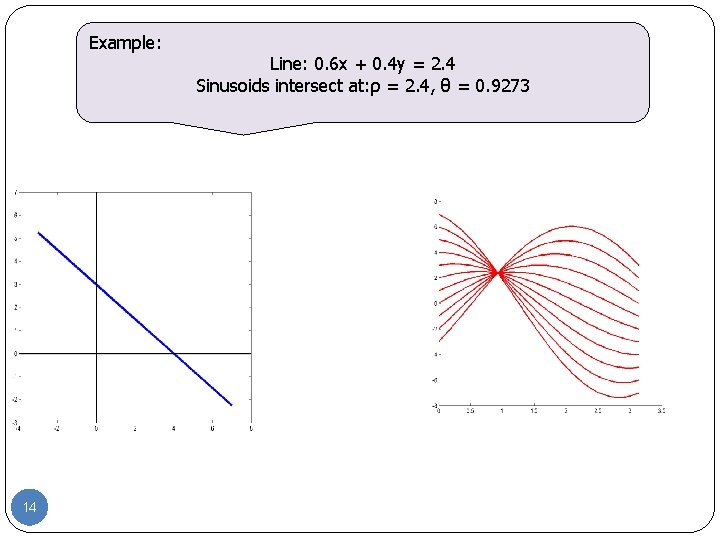
Example: 14 Line: 0. 6 x + 0. 4 y = 2. 4 Sinusoids intersect at: ρ = 2. 4, θ = 0. 9273

Let ρ= [−R, R] and θ= [0, pi ) For each edge point (xi , yi ), calculate: θ ‘ = xi cos θ ‘+ yi sin θ Accumulator: A(ρ, θ) = A(ρ, θ) + 1 Threshold the accumulator values to get parameters for detected lines Threshold at A(ρ, θ) = 30 Threshold at A(ρ, θ) = 20 Threshold at A(ρ, θ) = 15 15 ﺷﻨﺒﻪ ﺯﺍﺩﻩ

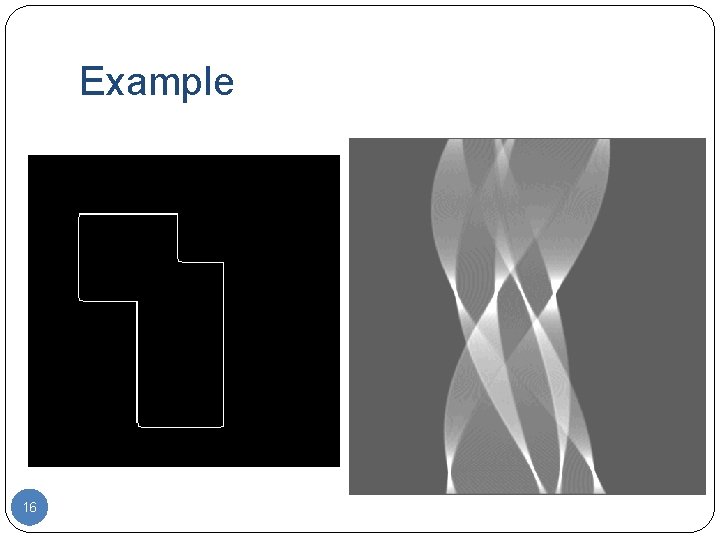
Example 16

Hough Transform Example with breaks in lines 17

Hough Transform Example with 1% salt and pepper noise 18

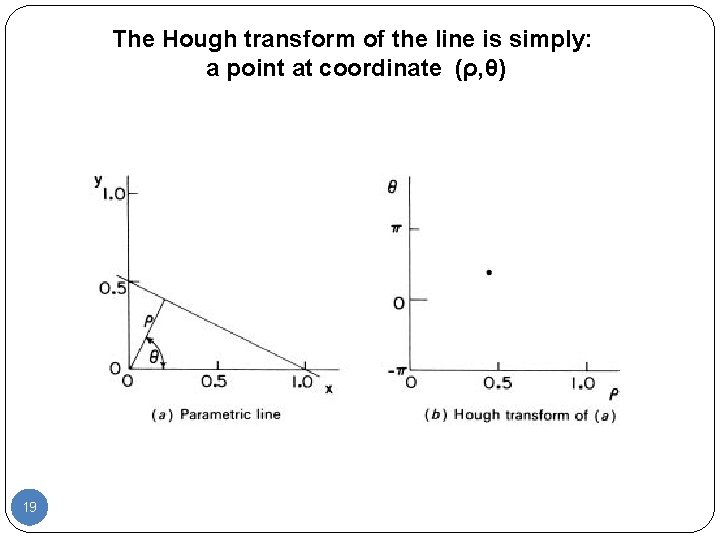
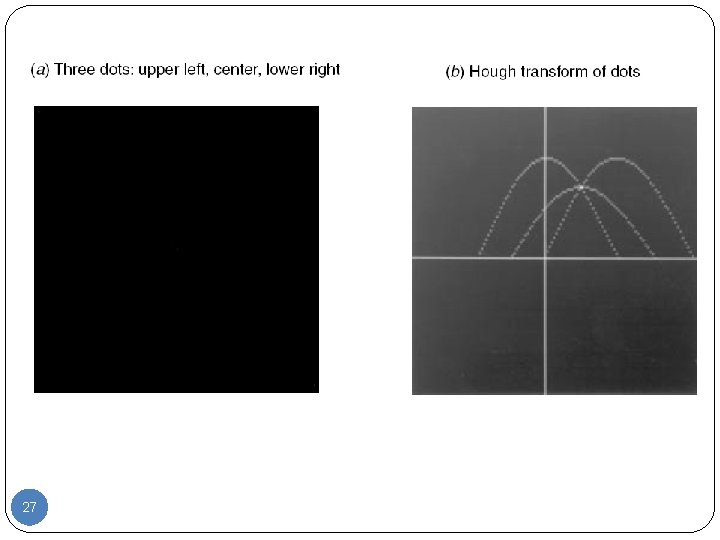
The Hough transform of the line is simply: a point at coordinate (ρ, θ) 19

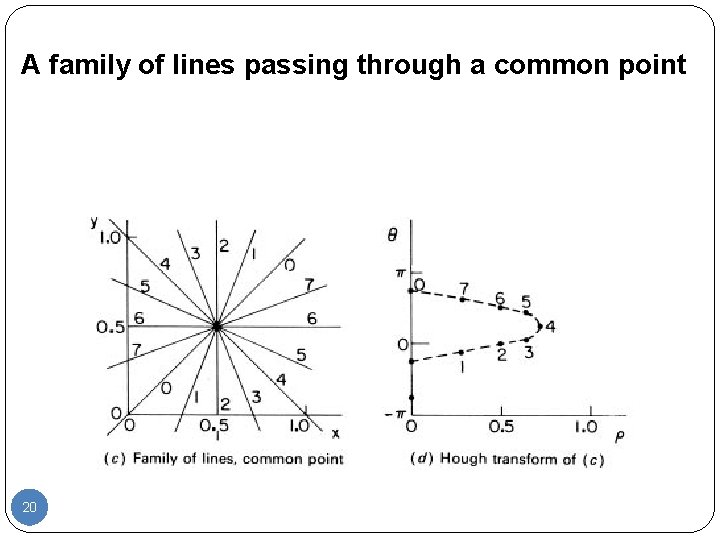
A family of lines passing through a common point 20

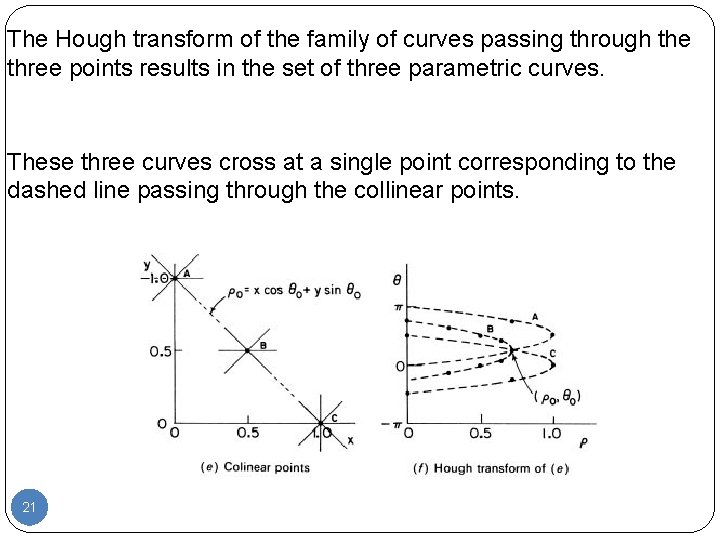
The Hough transform of the family of curves passing through the three points results in the set of three parametric curves. These three curves cross at a single point corresponding to the dashed line passing through the collinear points. 21

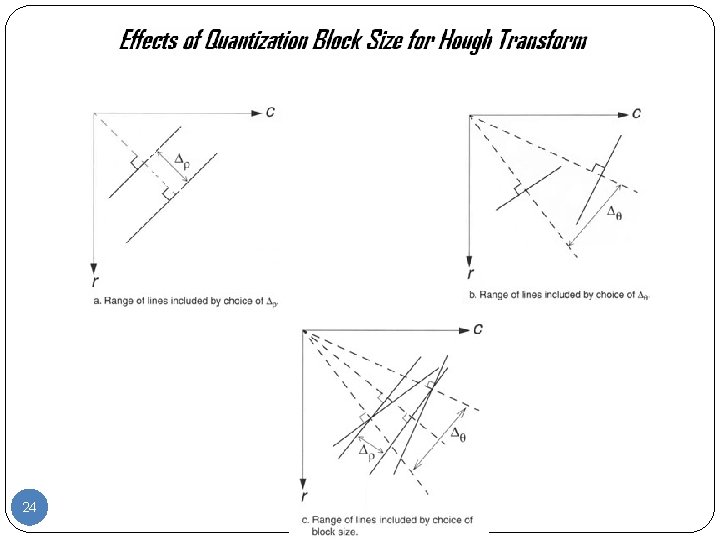
22

23

24

25

Example 26

27

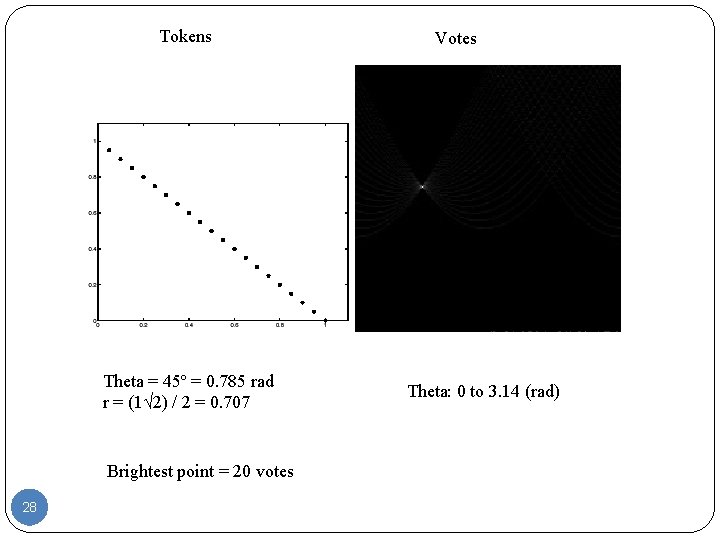
Tokens Theta = 45º = 0. 785 rad r = (1√ 2) / 2 = 0. 707 Brightest point = 20 votes 28 Votes Theta: 0 to 3. 14 (rad)

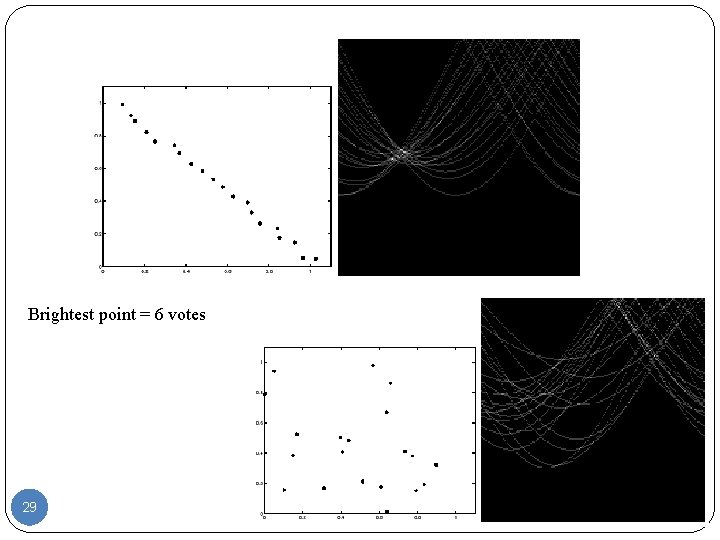
Brightest point = 6 votes 29

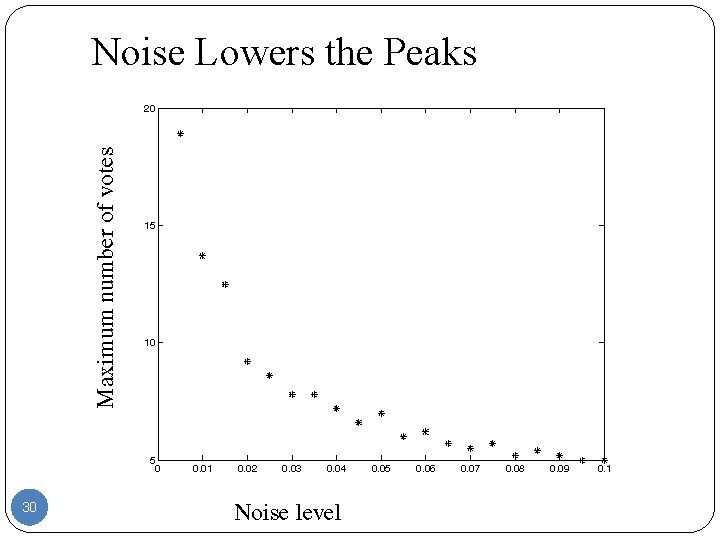
Noise Lowers the Peaks 30

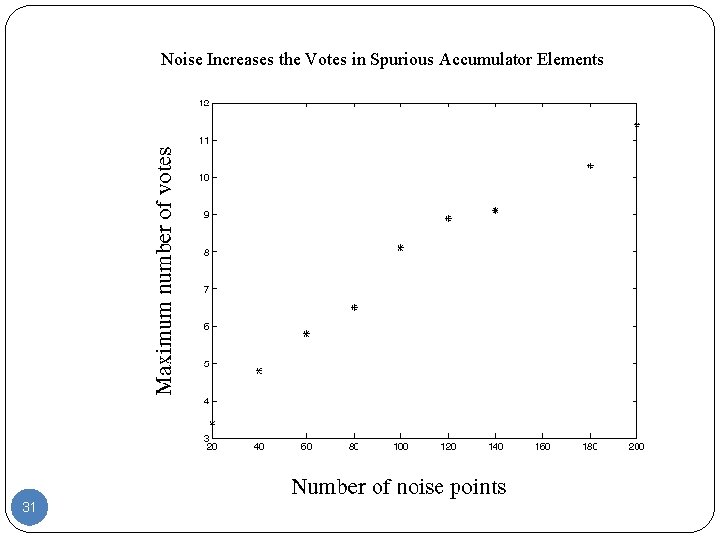
Noise Increases the Votes in Spurious Accumulator Elements 31

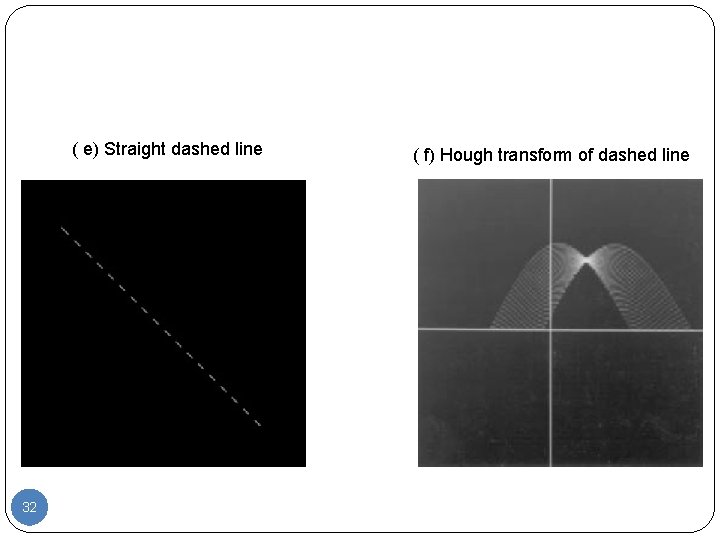
( e) Straight dashed line 32 ( f) Hough transform of dashed line

33

Advantages • Edges need not be connected • Complete object need not be visible • Key Idea: Edges VOTE for the possible model 34

Problems with HT 1)Exponential time and memory increase with the increase of the parameter numbers. 2) Sampling of parameter space is difficult. 3) Similar shapes might produce peaks in the Hough Space (wide ellipses might interfere with lines) 35

A city scene where the buildings are obstructed in fog 36

To find the true edges of the buildings 37

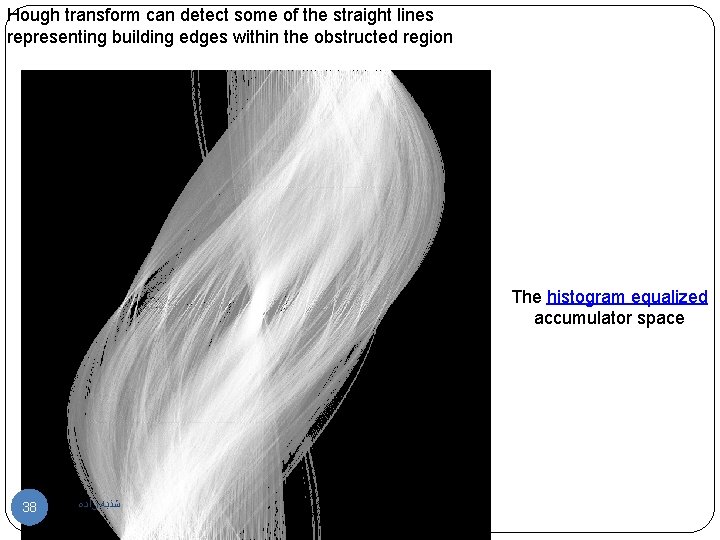
Hough transform can detect some of the straight lines representing building edges within the obstructed region The histogram equalized accumulator space 38 ﺷﻨﺒﻪ ﺯﺍﺩﻩ

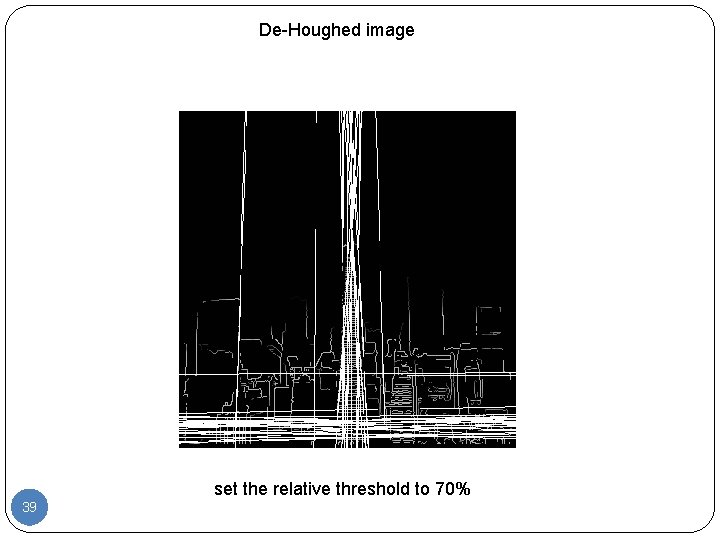
De-Houghed image set the relative threshold to 70% 39

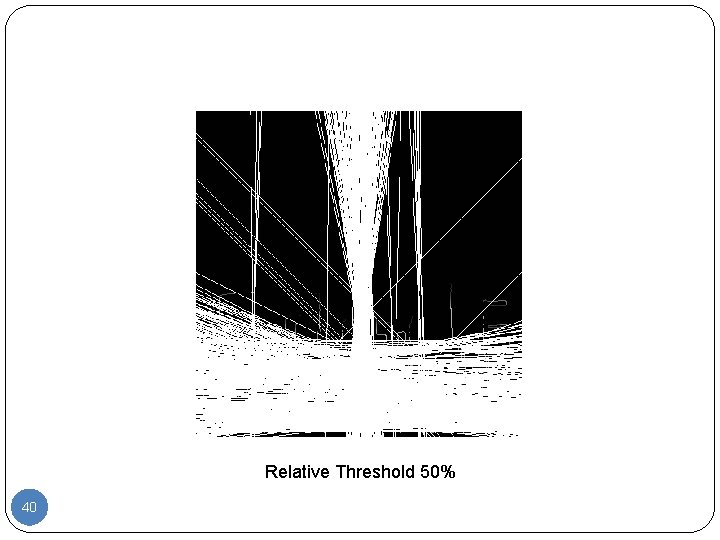
Relative Threshold 50% 40

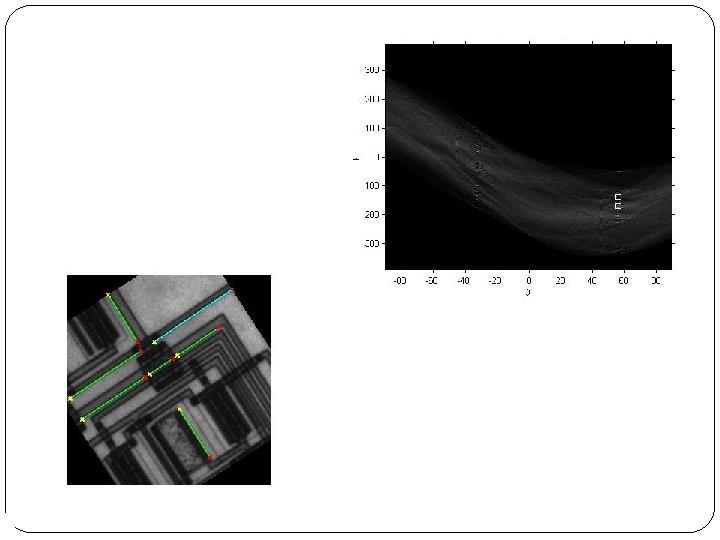
Street information is not available 41

Hough line detector is able to recover some of this information 42

Hough Transform By MATLAB I = imread('circuit. tif'); BW = edge(I, 'canny'); [H, T, R] = hough(BW); P = houghpeaks(H, 12, 'threshold', ceil(0. 3*max(H(: )))); lines = houghlines(BW, T, R, P, 'Fill. Gap', 5, 'Min. Length', 7); 43 ﺷﻨﺒﻪ ﺯﺍﺩﻩ

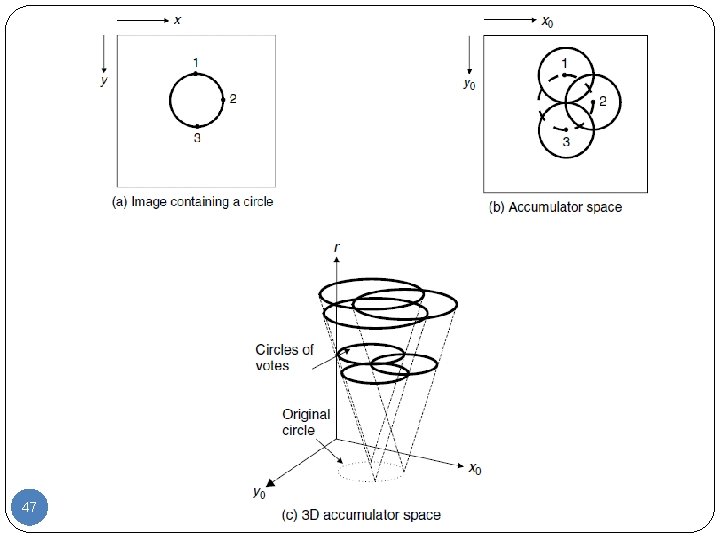
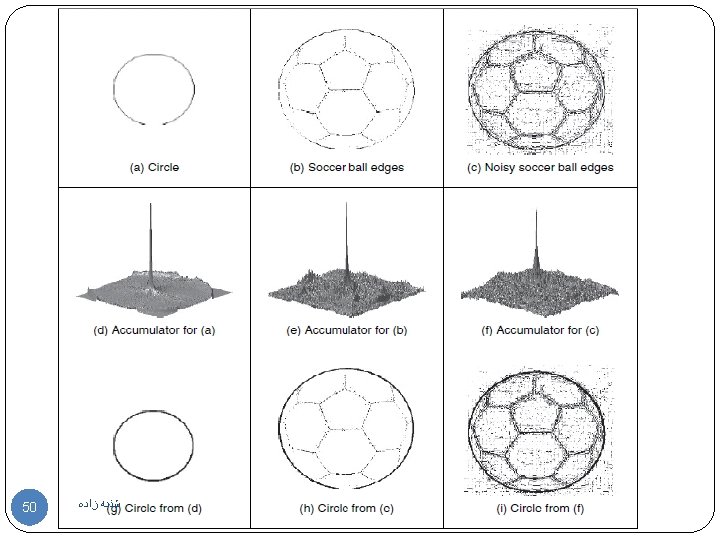
Hough transform for circles 45

Hough transform for circles 46

47

Implementation of the Hough transform for circles 48

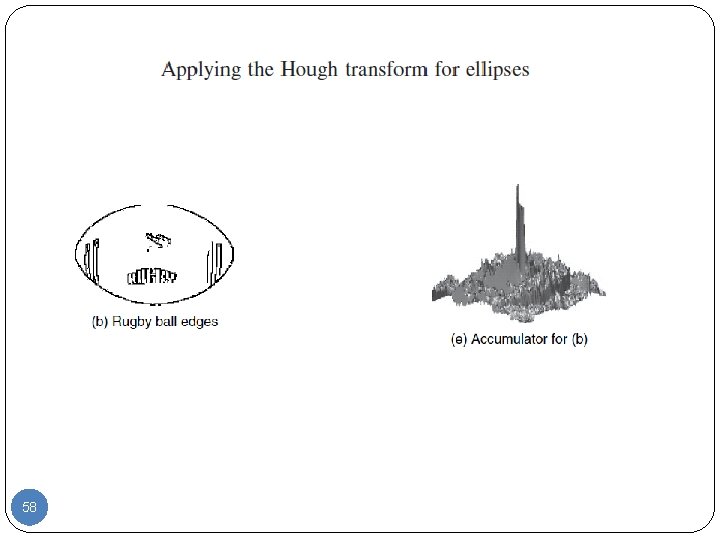
Hough transform for ellipses 52

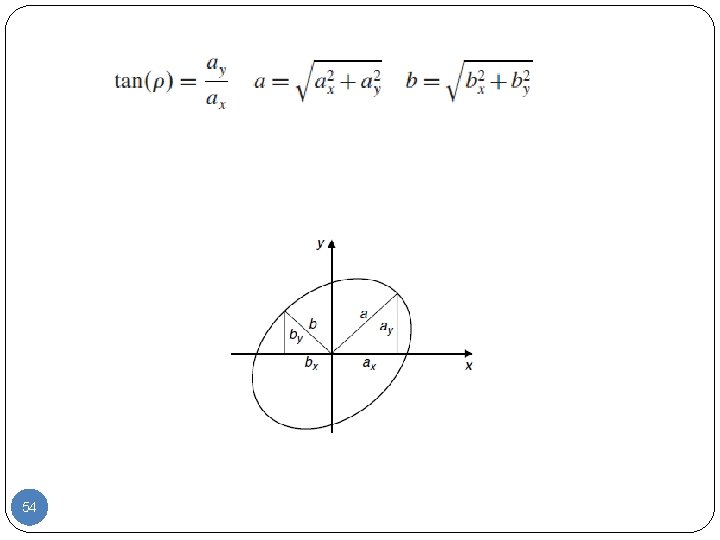
Circles are very important in shape detection since many objects have a circular shape. However, because of the camera’s viewpoint, circles do not always look like circles in images. We can define the mapping between the circle and an ellipse by a similarity transformation. 53

54

56

57

58

59