Horspool Algorithm Source Practical fast searching in strings

  • Slides: 16
Download presentation
Horspool Algorithm Source : Practical fast searching in strings R. NIGEL HORSPOOL Advisor: Prof.

Horspool Algorithm Source : Practical fast searching in strings R. NIGEL HORSPOOL Advisor: Prof. R. C. T. Lee Speaker: H. M. Chen 1

Definition of String Matching Problem • Given a pattern string P of length m

Definition of String Matching Problem • Given a pattern string P of length m and a text string T of length n, we would like to know whethere exists an occurrence of P in T. Text Pattern 2

Rule 2: Character Matching Rule • For any character X in T, find the

Rule 2: Character Matching Rule • For any character X in T, find the nearest X in P which is to the left of X in T. 3

• For each position of the window, we compare its last character(ß) with

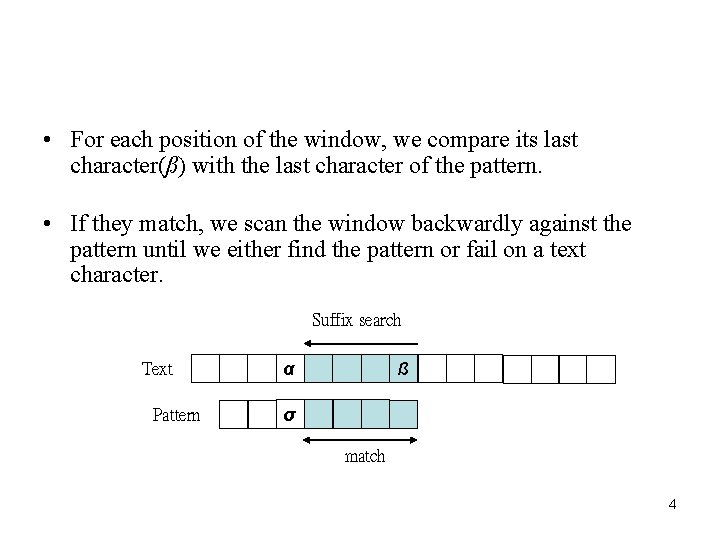
• For each position of the window, we compare its last character(ß) with the last character of the pattern. • If they match, we scan the window backwardly against the pattern until we either find the pattern or fail on a text character. Suffix search Text Pattern α ß σ match 4

• Then, no matter whethere is a match or not, we shift the

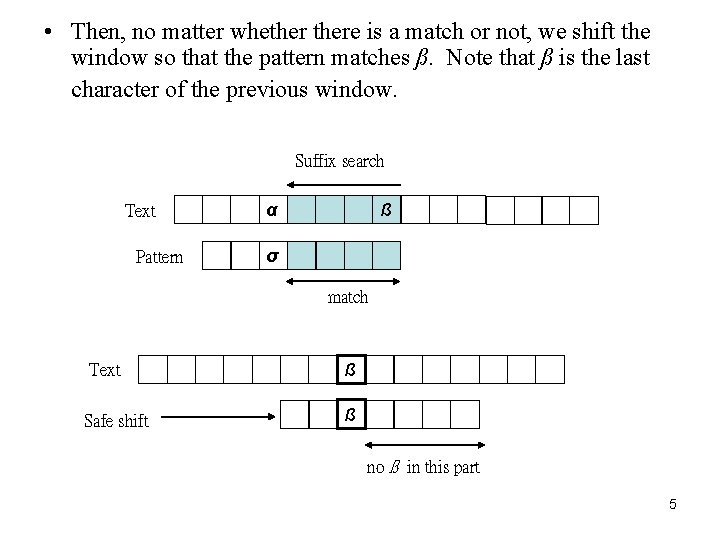
• Then, no matter whethere is a match or not, we shift the window so that the pattern matches ß. Note that ß is the last character of the previous window. Suffix search Text Pattern α ß σ match Text Safe shift ß ß no ß in this part 5

Preprocessing phase Hp. Bc table The value bm. Bc for a particular alphabet is

Preprocessing phase Hp. Bc table The value bm. Bc for a particular alphabet is defined as the rightmost position of that character in the pattern – 1. Example : T : GCATCGCAGAGAGTATACAGTACG P : GCAGAGAG 7 6 5 4 3 2 1 a A C G * Hp. Bc[a] 1 6 2 8 6

Pseudo code Horspool (P = p 1 p 2…pm, T = t 1 t

Pseudo code Horspool (P = p 1 p 2…pm, T = t 1 t 2…tn) Preprocessing For c ∑ Do d[c] ← m For j 1…m-1 Do d[pj] ← m - j Searching pos← 0 While pos ≤ n-m Do j ←m While j > 0 And tpos+j = pj Do j ← j-1 If j = 0 Then report an occurrence at pos+1 pos ← pos +d[tpos+m] End of while 7

Preprocessing phase for example : T : GCATCGCAGAGAGTATACAGTACG P : GCAGAGAG Step 1: For

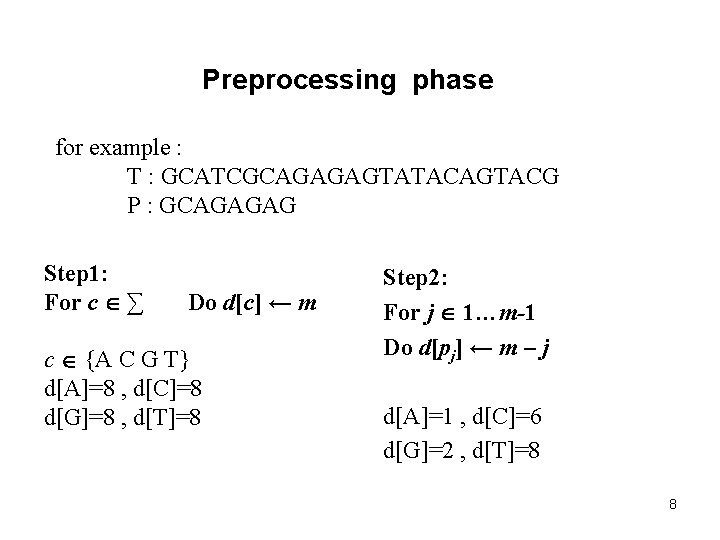
Preprocessing phase for example : T : GCATCGCAGAGAGTATACAGTACG P : GCAGAGAG Step 1: For c ∑ Do d[c] ← m c {A C G T} d[A]=8 , d[C]=8 d[G]=8 , d[T]=8 Step 2: For j 1…m-1 Do d[pj] ← m – j d[A]=1 , d[C]=6 d[G]=2 , d[T]=8 8

Example(1/3) 0 1 2 3 4 5 6 7 8 9 10 11 12

Example(1/3) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 GCATCGCAGAGAGTATACAGTACG GCAGAGAG pos ← 0 + d[t 0+7] , pos ← 0 + d[A], pos ← 1 pos ← pos +d[tpos+m] A C G * 1 6 2 8 GCATCGCAGAGAGTATACAGTACG GCAGAGAG pos ← 1 + d[t 1+7] , pos ← 1 + d[G], pos ← 3 GCATCGCAGAGAGTATACAGTACG GCAGAGAG pos ← 3 + d[t 3+7] , pos ← 3 + d[G], pos ← 5 9

Example(2/3) 0 1 2 3 4 5 6 7 8 9 10 11 12

Example(2/3) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 GCATCGCAGAGAGTATACAGTACG GCAGAGAG While j > 0 And tpos+j = pj Do j ← j-1 A C G * 1 6 2 8 If j = 0 Then report an occurrence at pos+1 pos ← 5 + d[t 5+7] , pos ← 5 + d[G], pos ← 7 GCATCGCAGAGAGTATACAGTACG GCAGAGAG pos ← 7 + d[t 7+7] , pos ← 7 + d[A], pos ← 8 GCATCGCAGAGAGTATACAGTACG GCAGAGAG pos ← 8 + d[t 8+7] , pos ← 8 + d[T], pos ← 16 10

Example(3/3) 0 1 2 3 4 5 6 7 8 9 10 11 12

Example(3/3) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 GCATCGCAGAGAGTATACAGTACG GCAGAGAG A C G * 1 6 2 8 pos ← 16 + d[t 16+7] , pos ← 16 + d[G], pos ← 18 pos > n-m // pos >23 -7 jump out of while loop 11

Example(1/2) for example : T : AGATACGATATATAC P : ATATA a A T *

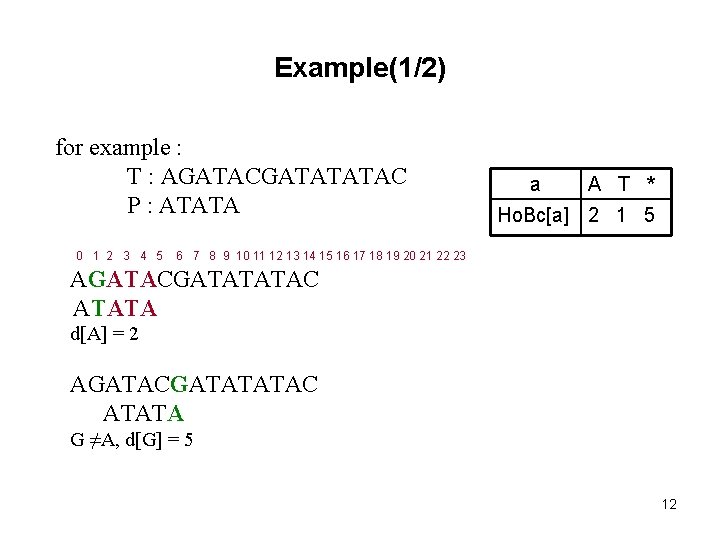
Example(1/2) for example : T : AGATACGATATATAC P : ATATA a A T * Ho. Bc[a] 2 1 5 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 AGATACGATATATAC ATATA d[A] = 2 AGATACGATATATAC ATATA G ≠A, d[G] = 5 12

Example(2/2) 0 1 2 3 4 5 6 7 8 9 10 11 12

Example(2/2) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 AGATACGATATATAC ATATA A T * 2 1 5 We verify backward the window and find the occurrence. We then shift by re-using the last character of the window, d[A] = 2 AGATACGATATATAC ATATA We find the pattern. We shift by the last character of then window, d[A] = 2. Then, pos > n-m and the search stops. 13

Time complexity • preprocessing phase in O(m+ п) time and O(п) space complexity. •

Time complexity • preprocessing phase in O(m+ п) time and O(п) space complexity. • searching phase in O(mn) time complexity. • the average number of comparisons for one text character is between 1/п and 2/(п+1). (п is the number of storing characters) 14

References • • AHO, A. V. , 1990, Algorithms for finding patterns in strings.

References • • AHO, A. V. , 1990, Algorithms for finding patterns in strings. in Handbook of Theoretical Computer Science, Volume A, Algorithms and complexity, J. van Leeuwen ed. , Chapter 5, pp 255 -300, Elsevier, Amsterdam. BAEZA-YATES, R. A. , RÉGNIER, M. , 1992, Average running time of the Boyer. Moore-Horspool algorithm, Theoretical Computer Science 92(1): 19 -31. BEAUQUIER, D. , BERSTEL, J. , CHRÉTIENNE, P. , 1992, Éléments d'algorithmique, Chapter 10, pp 337 -377, Masson, Paris. CROCHEMORE, M. , HANCART, C. , 1999, Pattern Matching in Strings, in Algorithms and Theory of Computation Handbook, M. J. Atallah ed. , Chapter 11, pp 11 -1 --11 -28, CRC Press Inc. , Boca Raton, FL. HANCART, C. , 1993. Analyse exacte et en moyenne d'algorithmes de recherche d'un motif dans un texte, Ph. D. Thesis, University Paris 7, France. HORSPOOL R. N. , 1980, Practical fast searching in strings, Software - Practice & Experience, 10(6): 501 -506. LECROQ, T. , 1995, Experimental results on string matching algorithms, Software Practice & Experience 25(7): 727 -765. STEPHEN, G. A. , 1994, String Searching Algorithms, World Scientific. 15

THANK YOU 16

THANK YOU 16