Horizontal Circular Motion l For Horizontal circular motion

Horizontal Circular Motion: l For Horizontal circular motion: Fc= Ff l Recall: l Ff = µFN Where FN is the normal force perpendicular to the surface.

Example: Determine the maximum speed at which a 1200 kg car can round a curve that has a radius of 35. 0 m, if the coefficient of friction between the tires and the road is 0. 60

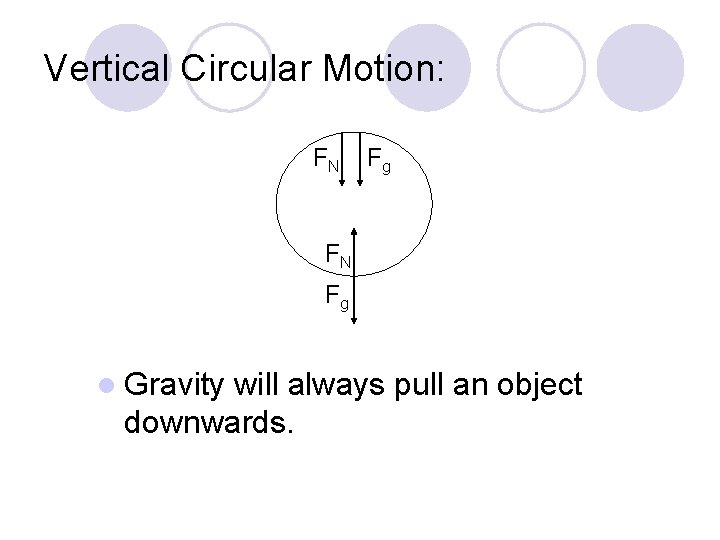
Vertical Circular Motion: FN Fg l Gravity will always pull an object downwards.

l Centripetal force is the net force acting towards the centre ¡ ¡ l With vertical circular motion this force changes. ¡ ¡ l Is equal to the sum of Fg and FN Fc = Fg + F N At top: Fg and FN are in the same directions At bottom: Fg and FN are in opposite directions. In order for an object to stay in a circular path, Fc ≥ Fg.

Example: A 800 kg roller coaster car full of people goes around a vertical loop that has a diameter of 65. 0 m. What minimum speed must the rollercoaster car have at the top of the vertical loop to stay on the track?

Example: A 1. 7 kg object is swung from the end of a 0. 60 m string in a vertical circle. If the time of one revolution is 1. 1 s, what is the tension in the string: (a) when it is at the top? (b) when it is at the bottom?

Homework: l Page 259 #1 -3 l Page 262 #1 -2 l Page 264 #1 -3

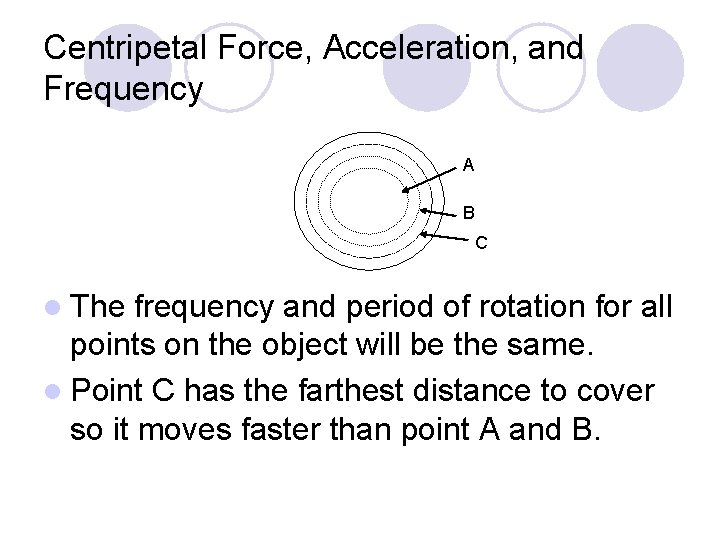
Centripetal Force, Acceleration, and Frequency A B C l The frequency and period of rotation for all points on the object will be the same. l Point C has the farthest distance to cover so it moves faster than point A and B.

We can derive equations force and acceleration using frequency and period: l We know: and

By substituting the velocity equation into the acceleration formula:

Centripetal Force:

Period is just the inverse of frequency:

Example: The compressor blade in a jet engine has a diameter of 53. 0 cm and turns at a rate of 14 350 rpm. Determine the magnitude of centripetal force at the tip of each compressor blade.

Homework: l Page 267 #1 -2