Horizontal Asymptotes of Rational Functions Lesson 10 6

Horizontal Asymptotes of Rational Functions Lesson 10. 6

Lecture Part I

Review – Graphing Functions in Transformation Form � Graphing functions in this form: �Graph �Translate horizontally units. �Vertical asymptote: �Horizontal asymptote: h units and vertically k

Rational Functions in Form � 3 Types of Examples Dominant Term in denominator Dominant Terms Dominant Term in numerator AND denominator

Dominant term in DENOMINATOR Denominator gets bigger faster than numerator!!

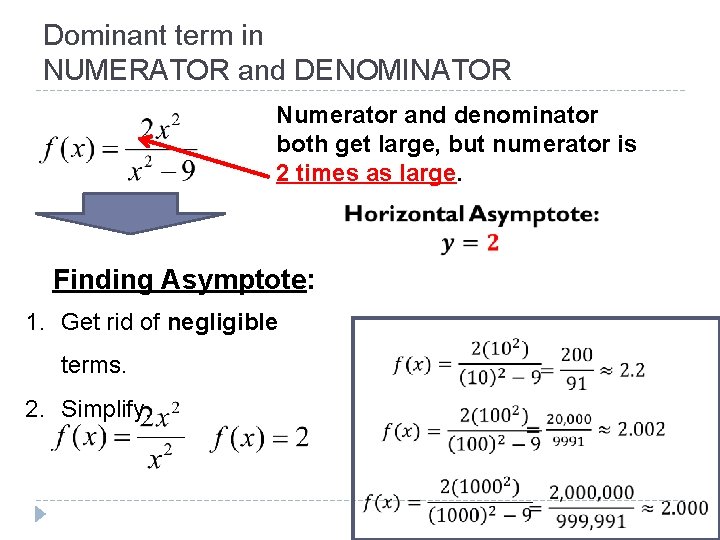
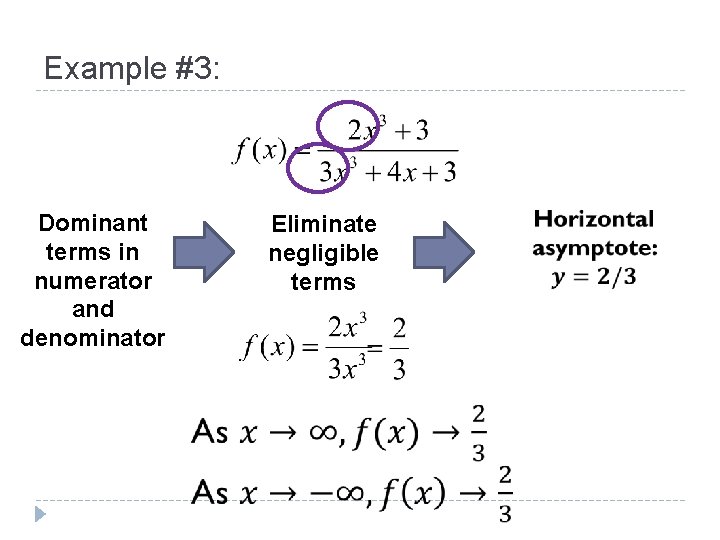
Dominant term in NUMERATOR and DENOMINATOR Numerator and denominator both get large, but numerator is 2 times as large. Finding Asymptote: 1. Get rid of negligible terms. 2. Simplify.

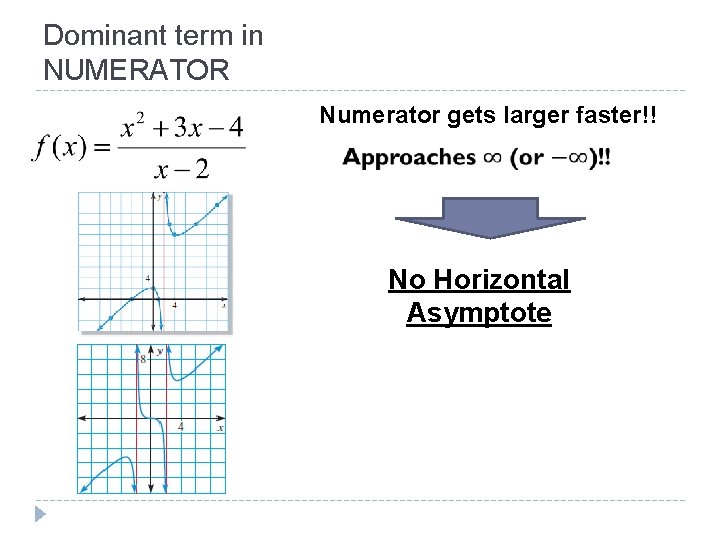
Dominant term in NUMERATOR Numerator gets larger faster!! No Horizontal Asymptote

Intermission

Check for Understanding � Annotate your notes –underline key terms; write reminders in the cue column �Write a summary in your notes with the key points: � For functions with the dominant term in the denominator, the horizontal asymptote is ______ � For functions with the dominant term in the numerator, the horizontal asymptote is ______ � For functions with the same degree in the numerator and denominator, the horizontal asymptote is ______

Lecture Part II

Characteristics of Graphs of Rational Functions �

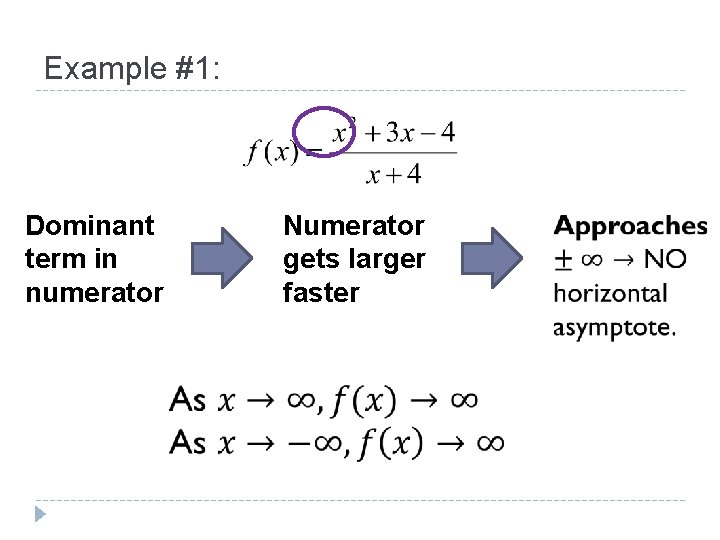
Example #1: Dominant term in numerator Numerator gets larger faster

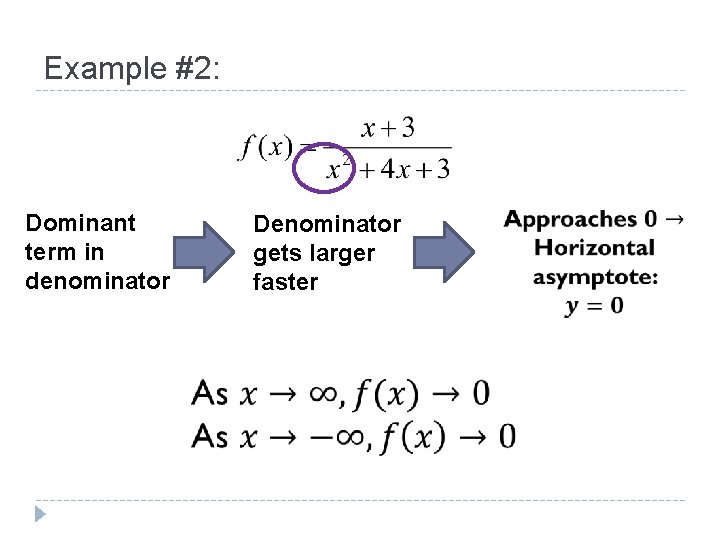
Example #2: Dominant term in denominator Denominator gets larger faster

Example #3: Dominant terms in numerator and denominator Eliminate negligible terms

End of College Lecture

Backup

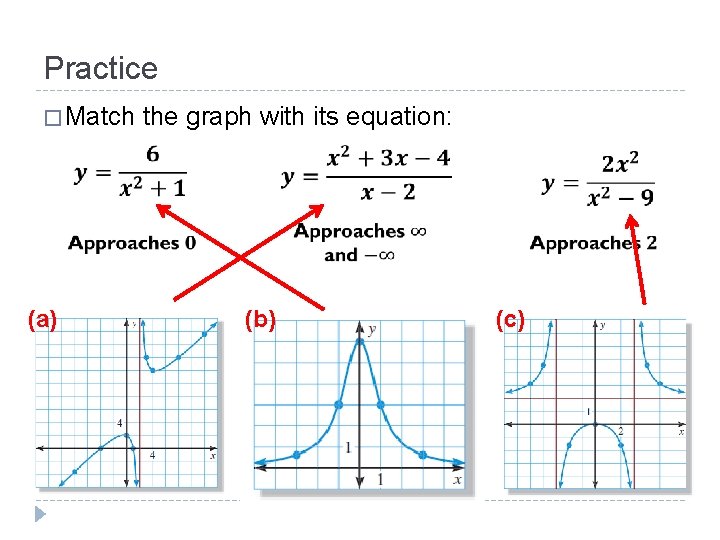
Practice � Match the graph with its equation: (a) (b) (c)

Characteristics of Graphs of Rational Functions �

Example #1 �

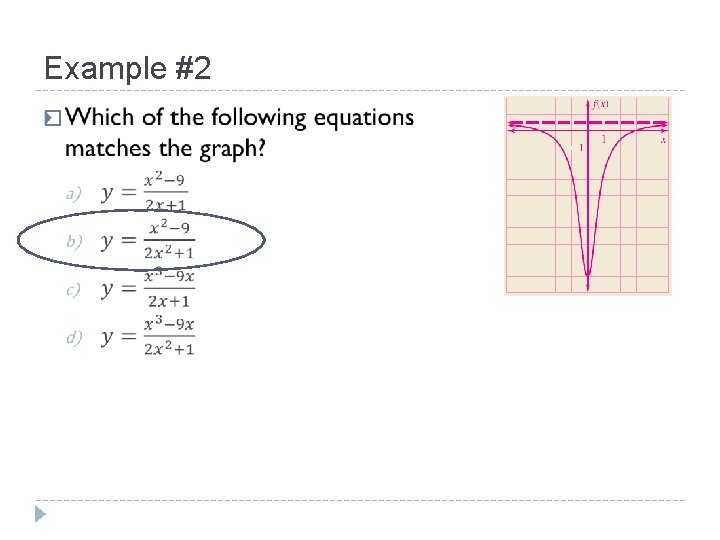
Example #2 �

Practice � Complete Problem Set C

Practice � Complete Problem Set A

Characteristics of Graphs of Rational Functions �Excluded Values � Values that make denominator equal zero.

Characteristics of Graphs of Rational Functions �Types of Excluded Values: �Holes (Excluded values that are cancelled out!) �Vertical Asymptotes (other excluded values)

Example #1: � Identify the excluded values for the following equation. State which values are HOLES and which values are VERTICAL ASYMPTOTES. Vertical Asymptotes: NONE

Example #2: � Identify the excluded values for the following equation. State which values are HOLES and which values are VERTICAL ASYMPTOTES. Holes: NONE

Example #3: � Identify the excluded values for the following equation. State which values are HOLES and which values are VERTICAL ASYMPTOTES. Holes: Vertical Asymptote:

Practice � Complete Problem Set B

Review �

Example #1 �

Example #2 �

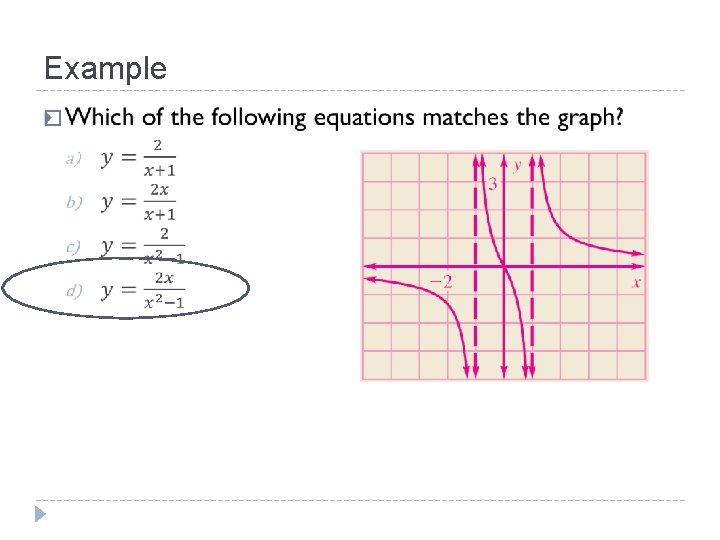
Example �

Practice � Complete Problem Set D