Hopfield Network Taiwan Evolutionary Intelligence Laboratory 20160318 Group

Hopfield Network Taiwan Evolutionary Intelligence Laboratory 2016/03/18 Group Meeting Presentation

Artificial Neural Network • Why “neural” ? – Sets of adaptive weights tuned by learning algorithm – Capability of approximating non-linear functions • Feedforward Network – Directional Acyclic Graph – Function mapping • Recurrent Network – Internal directed cycles – Internal states as memories

Feedforward Network • Single-Layered perceptron – Linear separation • Multiple-Layered perceptron (MLP) – Solve Non-linear problems – Backpropagation algorithm (1986) • Minimally connected – A decision tree – Training for maximum entropy

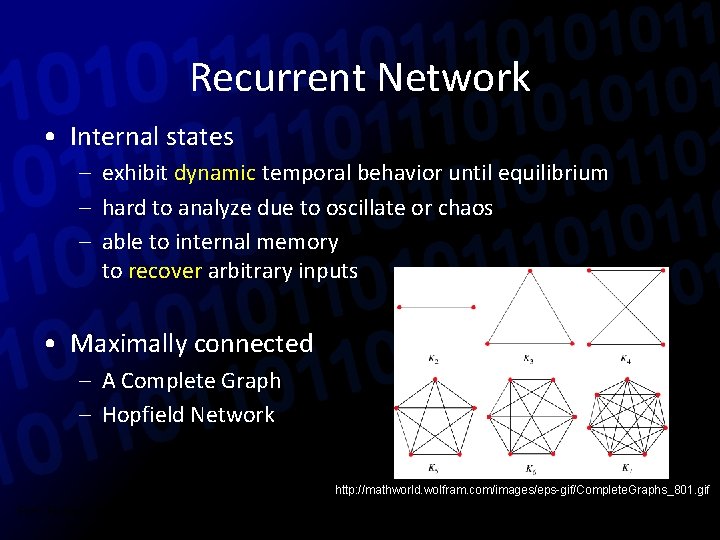
Recurrent Network • Internal states – exhibit dynamic temporal behavior until equilibrium – hard to analyze due to oscillate or chaos – able to internal memory to recover arbitrary inputs • Maximally connected – A Complete Graph – Hopfield Network http: //mathworld. wolfram. com/images/eps-gif/Complete. Graphs_801. gif Ref: Risto Miikkulainen. (2010). Neuroevolution. In Encyclopedia of Machine Learning, New. York 2010. Springer.

Hopfield Network • Invented by John Hopfield in 1982 • Single layered Complete Graph with symmetric weights – Symmetric weights gives global energy function • Associative Memory for binary pattern vectors • Pattern stored as weight with good resistant to noise http: //www. nnwj. de/uploads/pics/1_2 -hopfield-net. gif Ref: Risto Miikkulainen. (2010). Neuroevolution. In Encyclopedia of Machine Learning, New. York 2010. Springer.

Hopfield Network • Invented by John Hopfield in 1982 – An electronic circuits – “Solving problems … without the need to follow the circuit dynamics in detail” Ref: Risto Miikkulainen. (2010). Neuroevolution. In Encyclopedia of Machine Learning, New. York 2010. Springer.

Hopfield Network • Solving Traveling Salesman Problem Ref: Risto Miikkulainen. (2010). Neuroevolution. In Encyclopedia of Machine Learning, New. York 2010. Springer.

Hopfield Network • Task-Assignment Problem Ref: Risto Miikkulainen. (2010). Neuroevolution. In Encyclopedia of Machine Learning, New. York 2010. Springer.

Hopfield Network • Single layered Complete Graph with symmetric weights • Hebbian learning rule: – Introduced by Donald O. Hebb in 1949 – Cells that fire together, wire together Ref: Risto Miikkulainen. (2010). Neuroevolution. In Encyclopedia of Machine Learning, New. York 2010. Springer.

Hopfield Network • Hebbian learning rule: – Cells that fire together, wire together • Learning rules: – Local : each weight is updated using neurons information on either side of connection – Incremental : update of new weight only depends on new pattern and old values, not old pattern Ref.

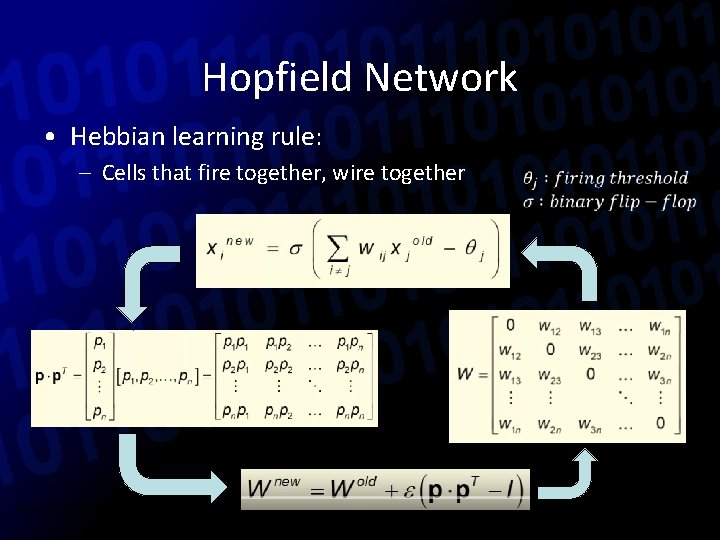
Hopfield Network • Hebbian learning rule: – Cells that fire together, wire together Ref: Risto Miikkulainen. (2010). Neuroevolution. In Encyclopedia of Machine Learning, New. York 2010. Springer.

Hopfield Network • Synchronous Update : – Output is the next epoch – Possible Oscillation • Asynchronous update : – Randomly pick one to update – Could converge Ref: Risto Miikkulainen. (2010). Neuroevolution. In Encyclopedia of Machine Learning, New. York 2010. Springer.

Hopfield Network • Energy Function: • The Energy decreases each time a neuron fires Ref: Risto Miikkulainen. (2010). Neuroevolution. In Encyclopedia of Machine Learning, New. York 2010. Springer.

Hopfield Network • Energy Function: • The Energy decreases each time a neuron fires • Initialization: – Repeated updates an input pattern until convergence – Hopfield “remember” the pattern as local minimum Ref: Risto Miikkulainen. (2010). Neuroevolution. In Encyclopedia of Machine Learning, New. York 2010. Springer.

Hopfield Network • Initialization: – Repeated updates an input pattern until convergence – Hopfield “remember” the pattern as local minimum • The Energy decreases each time a neuron fires Ref: Risto Miikkulainen. (2010). Neuroevolution. In Encyclopedia of Machine Learning, New. York 2010. Springer.

Hopfield Network • Associative memory: – connection between conceptual entities – Retrieval of the most similar vector in the network – Rizzuto and Kahana (2001) use a probabilistic-learning algorithm to fix the weights of the network – Learning stage vs. Recall stage Ref: Risto Miikkulainen. (2010). Neuroevolution. In Encyclopedia of Machine Learning, New. York 2010. Springer.

Hopfield Network • Content-addressable memory – Access an item by just knowing part of its content • Pattern stored as weight with good resistant to noise – Robust against weight lose or input noise http: //cdn. infoq. com/statics_s 2_20160301 -0105 u 1/resource/articles/emotion-cognition/en/resources/6_hopfield_net. jpg Ref: Risto Miikkulainen. (2010). Neuroevolution. In Encyclopedia of Machine Learning, New. York 2010. Springer.

Hopfield Network • Ref: Risto Miikkulainen. (2010). Neuroevolution. In Encyclopedia of Machine Learning, New. York 2010. Springer.

Hopfield Network • Unsupervised Learning: – Not knowing the correct answer, i. e. not error driven – Most leaning methods are supervised learning modifying weights by error – Hebbian Learing method depends on each output – Converge to a minimum Energy (attractor) Ref: Risto Miikkulainen. (2010). Neuroevolution. In Encyclopedia of Machine Learning, New. York 2010. Springer.

Discussion • Symmetric weights gives global energy function – There exist an energy function in ILS? – Is it possible to use a dynamic network to generate masks between generations? – Asynchronous update bits? Ref: Risto Miikkulainen. DSMGA-II (2010). paper Neuroevolution. In Encyclopedia of Machine Learning, New. York 2010. Springer.

Discussion • Associative memory allows Access an item by just knowing part of its content – Is Optimal Mixing finding the relative associative memory? – New way of mixing? Or retrieving masks like TSP? – GA is also dynamic and not error-driven! Ref: Risto Miikkulainen. (2010). paper Neuroevolution. In Encyclopedia of Machine Learning, New. York 2010. Springer. DSMGA-II http: //www. nnwj. de/uploads/pics/1_2 -hopfield-net. gif

Reference 1. David W. Tank, John J. Hopfield. Collective Computation in Neuronlike Circuits. Sci. Amer. , 257 (6) (1987), pp. 104– 114. 2. David W. Tank, John J. Hopfield. Computing with Neural Circuits: A Model. Science, New Series, Vol. 233, No. 4764 (Aug. 8, 1986), 625 -633. 3. http: //yuhmoon. myweb. hinet. net/ann/chapter 04. ppt 4. http: //ktchenkm. iem. mcut. edu. tw/xms/read_attach. php? id= 934 5. https: //www. youtube. com/watch? v=gf. PUWw. Bk. XZY 6. https: //www. youtube. com/watch? v=7 p_a. YVFx-qo