Hookes Law Hookes Law In the 1600 s

Hooke’s Law

Hooke’s Law In the 1600 s, a scientist called Robert Hooke discovered a law for elastic materials. Hooke's achievements were extraordinary - he made the first powerful microscope and wrote the first scientific bestseller, Micrographia. He even coined the word ‘Cell’.

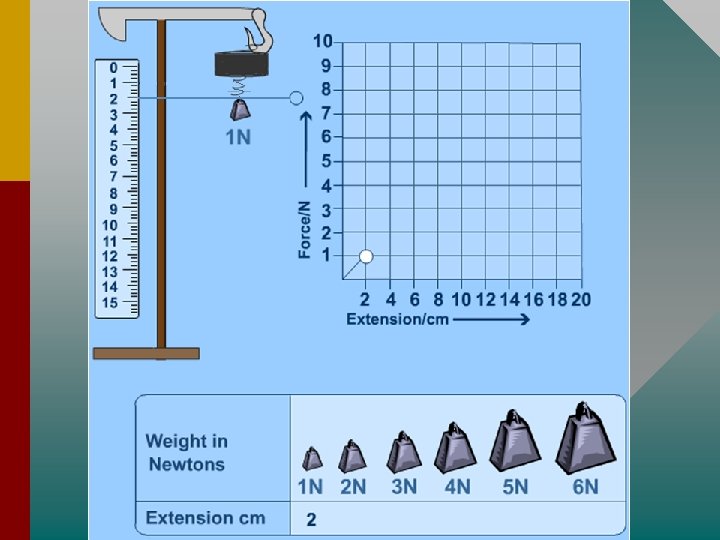
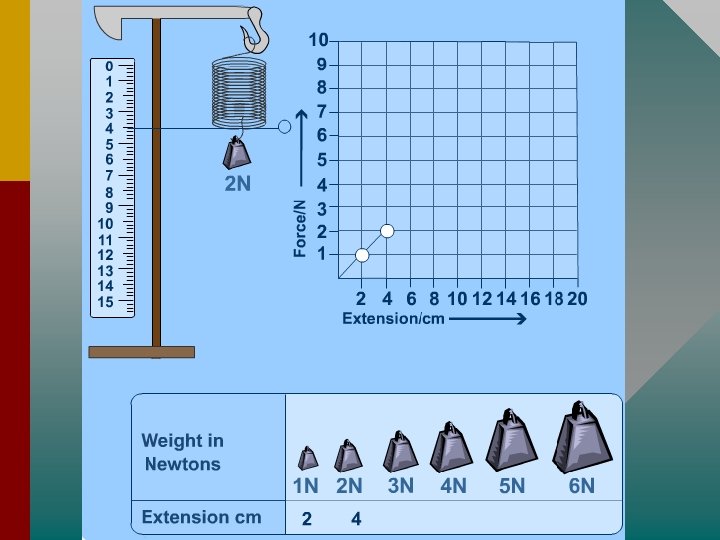
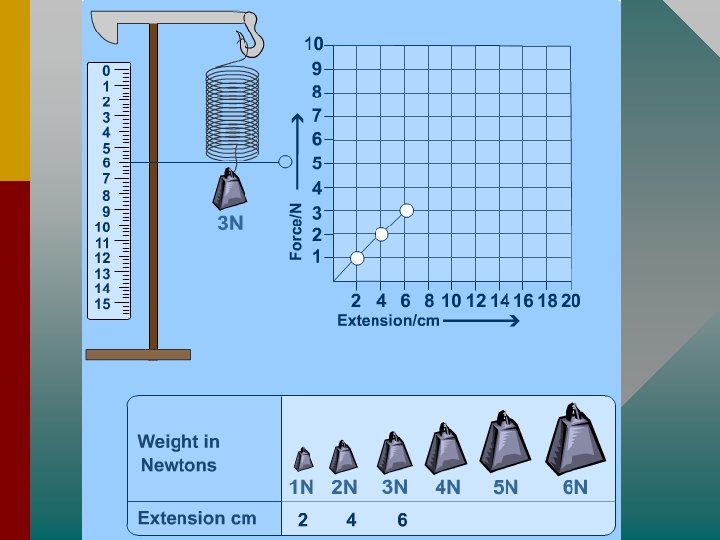
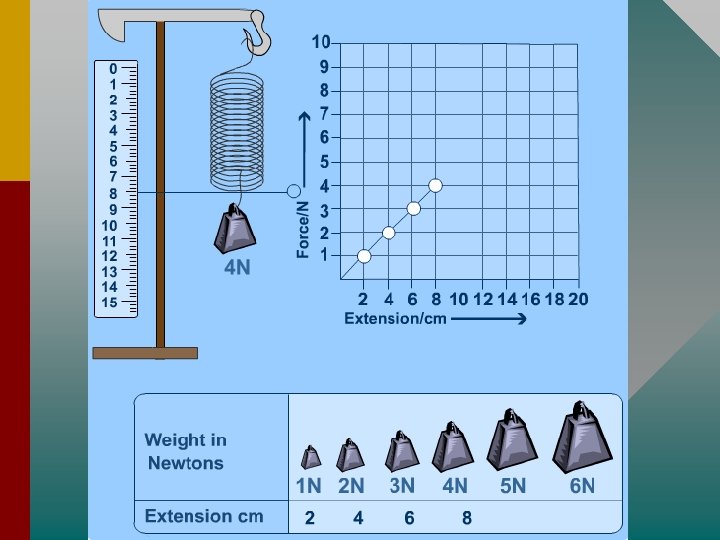
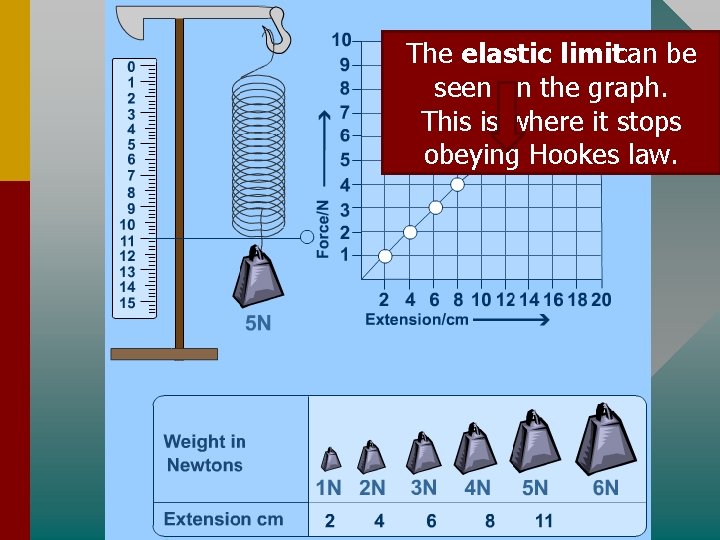
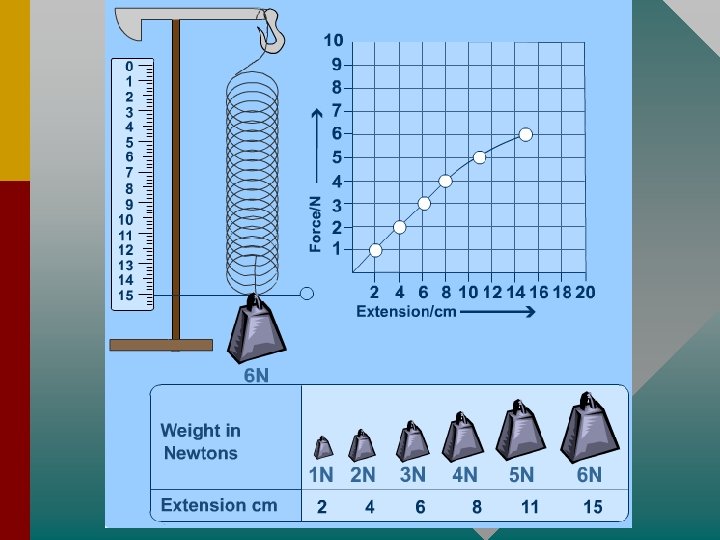
Hooke's Law, elastic and plastic behaviour • If a material returns to its original size and shape when you remove the forces stretching or deforming it (reversible deformation), we say that the material is demonstrating elastic behaviour. • A plastic(or inelastic) material is one that stays deformed after you have taken the force away. If deformation remains (irreversible deformation) after the forces are removed then it is a sign of plastic behaviour. • If you apply too big a force a material will lose its elasticity. • Hooke discovered that the amount a spring stretches is proportional to the amount of force applied to This it. means if you double the force its extension will double, if you triple the force the extension will triple and so on.

The elastic limitcan be seen on the graph. This is where it stops obeying Hookes law.

You can write Hooke's law as an equation: F = k∆ x Where: • F is the applied force (in newtons, N), • x is the extension (in metres, m) and • k is the spring constant (in N/m). • The extension ∆x (delta-x) is sometimes written e or ∆l. You find the extension from: • ∆x = stretched length – original length.

• Hold on a minute, K? Spring Constant? ! The spring constant measures how stiff the spring is. • The larger the spring constant the stiffer the spring. • You may be able to see this by looking at the graphs below: k is measured in units of newtons per metre (Nm -1).

Example • A spring is 0. 38 m long. When it is pulled by a force of 2. 0 N, it stretches to 0. 42 m. What is the spring constant? Assume the spring behaves elastically. ∆x = Stretched length – Original length = Extension, . F=k∆x 2. 0 N = k x 0. 04 m 0. 42 m – 0. 38 m = 0. 04 m So, k = 2. 0 N = 50 N m 0. 04 m

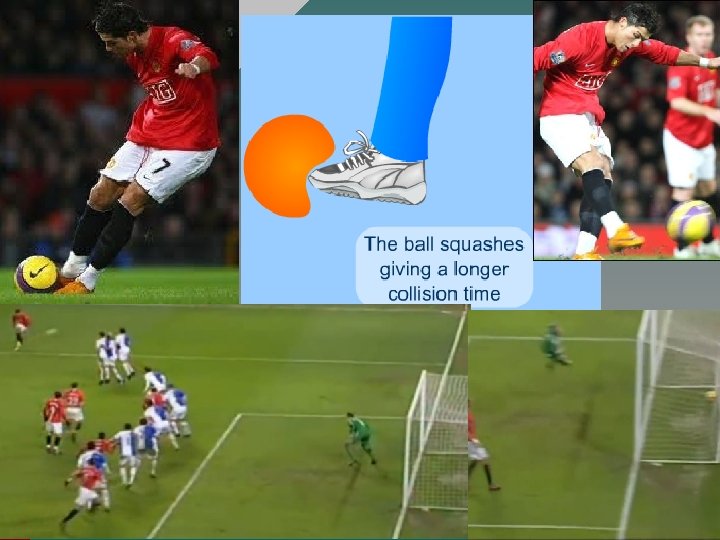
Elastic behaviour – Car Safety • Elastic behaviour is very important in car safety, as car seatbelts are made from elastic materials. However, after a crash they must be replaced as they will go past their elastic limit. • Why have seat belts that are elastic? • Why not just have very rigid seatbelts that would keep you firmly in place? • The reason for this, is that it would be very dangerous and cause large injuries. This is because it would slow your body down too quickly. The quicker a collision, the bigger the force that is produced.

• Key Definitions Hooke’s Law = The amount a spring stretches is proportional to the amount of force applied to it. • The spring constant measures how stiff the spring is. The larger the spring constant the stiffer the spring. • A Diagram to show Hooke’s Law F=k∆x

Photo by Mark Tippens A TRAMPOLINE exerts a restoring force on the jumper that is directly proportional to the average force required to displace the mat. Such restoring forces provide the driving forces necessary for objects that oscillate with simple harmonic motion.

Objectives: After finishing this unit, you should be able to: • Write and apply Hooke’s Law for objects moving with simple harmonic motion. • Write and apply formulas for finding the frequency f, period T, velocity v, or acceleration a in terms of displacement x or time t. • Describe the motion of pendulums and calculate the length required to produce a given frequency.

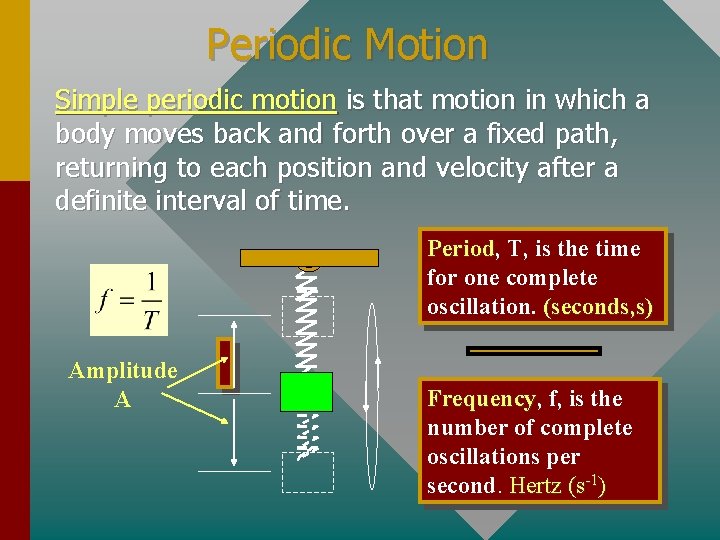
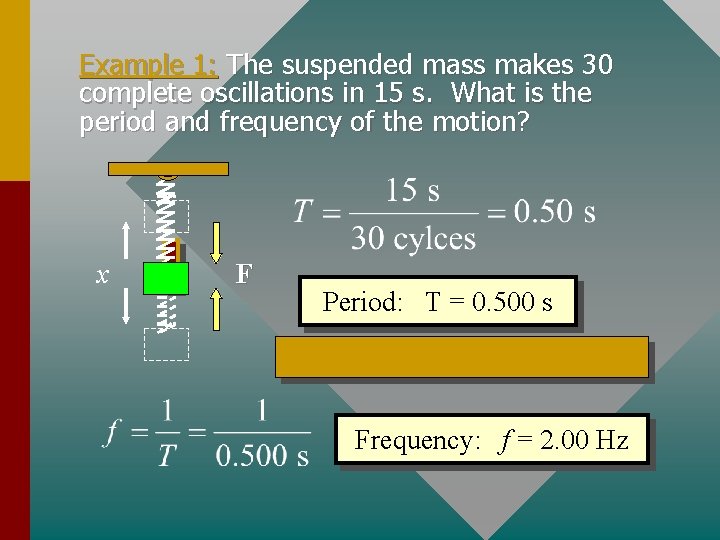
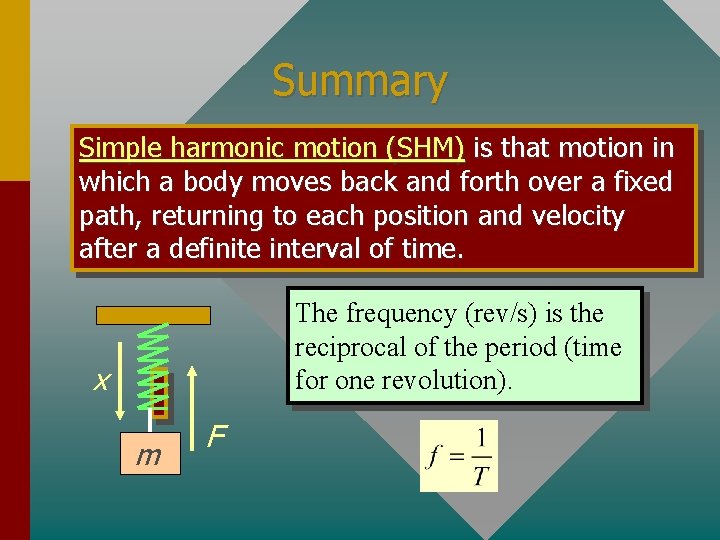
Periodic Motion Simple periodic motion is that motion in which a body moves back and forth over a fixed path, returning to each position and velocity after a definite interval of time. Period, Period T, is the time for one complete oscillation. (seconds, s) Amplitude A Frequency, Frequency f, is the number of complete oscillations per second. Hertz (s-1)

Example 1: The suspended mass makes 30 complete oscillations in 15 s. What is the period and frequency of the motion? x F Period: T = 0. 500 s Frequency: f = 2. 00 Hz

Simple Harmonic Motion, SHM Simple harmonic motion is periodic motion in the absence of friction and produced by a restoring force that is directly proportional to the displacement and oppositely directed. x F A restoring force, F, acts in the direction opposite the displacement of the oscillating body. F = -kx

Hooke’s Law When a spring is stretched, there is a restoring force that is proportional to the displacement. F = -kx x m F The spring constant k is a property of the spring given by: k= DF Dx

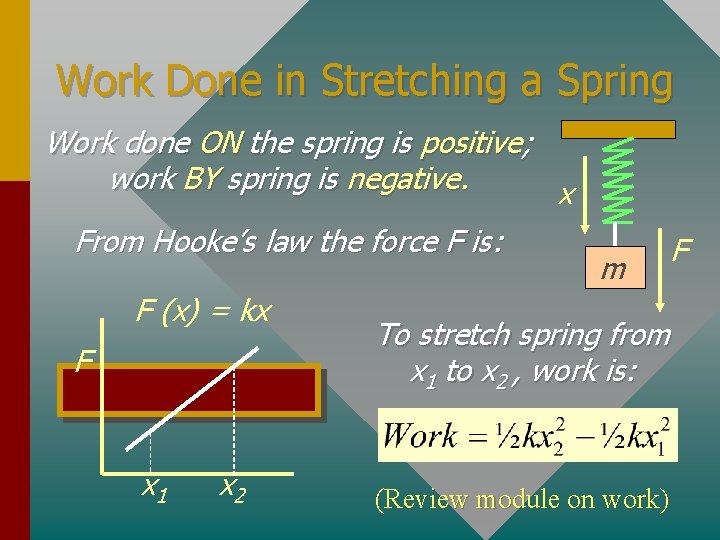
Work Done in Stretching a Spring Work done ON the spring is positive; work BY spring is negative. x From Hooke’s law the force F is: F (x) = kx F x 1 x 2 m F To stretch spring from x 1 to x 2 , work is: (Review module on work)

Example 2: A 4 -kg mass suspended from a spring produces a displacement of 20 cm. What is the spring constant? The stretching force is the weight (W = mg) of the 4 -kg mass: 20 cm F = (4 kg)(9. 8 m/s 2) = 39. 2 N F m Now, from Hooke’s law, the force constant k of the spring is: k= DF Dx = 39. 2 N 0. 2 m k = 196 N/m

Example 2(cont. : The mass m is now stretched a distance of 8 cm and held. What is the potential energy? (k = 196 N/m) The potential energy is equal to the work done in stretching the spring: 0 U = 0. 627 J 8 cm F m

Displacement in SHM x m x = -A x=0 x = +A • Displacement is positive when the position is to the right of the equilibrium position (x = 0) and negative when located to the left. • The maximum displacement is called the amplitude A.

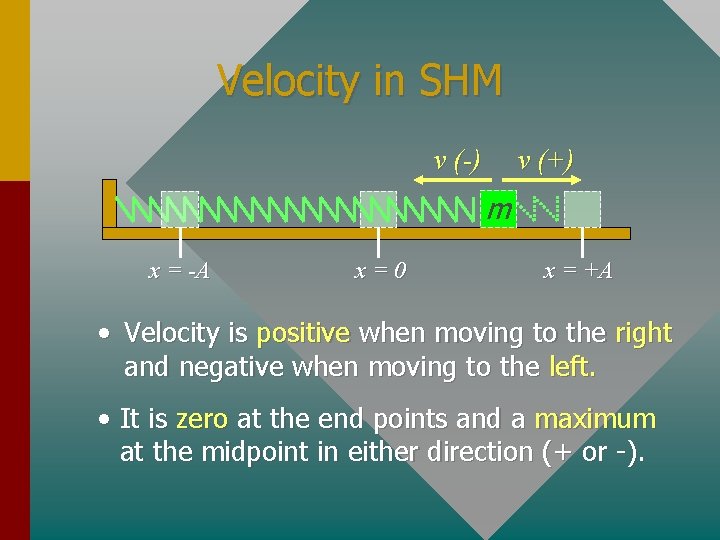
Velocity in SHM v (-) v (+) m x = -A x=0 x = +A • Velocity is positive when moving to the right and negative when moving to the left. • It is zero at the end points and a maximum at the midpoint in either direction (+ or -).

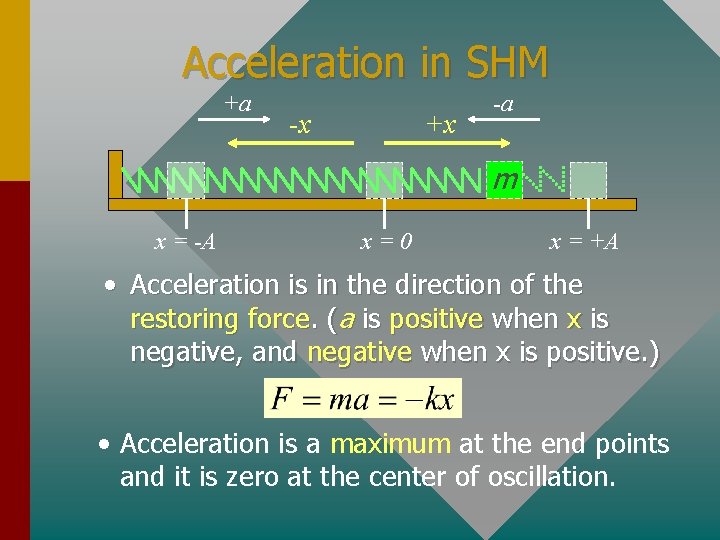
Acceleration in SHM +a -x +x -a m x = -A x=0 x = +A • Acceleration is in the direction of the restoring force. (a is positive when x is negative, and negative when x is positive. ) • Acceleration is a maximum at the end points and it is zero at the center of oscillation.

Acceleration vs. Displacement x a v m x = -A x=0 x = +A Given the spring constant, the displacement, and the mass, the acceleration can be found from: or Note: Acceleration is always opposite to displacement.

Example 3: A 2 -kg mass hangs at the end of a spring whose constant is k = 400 N/m. The mass is displaced a distance of 12 cm and released. What is the acceleration at the instant the displacement is x = +7 cm? a = -14. 0 m/s 2 a m Note: When the displacement is +7 cm (downward), the acceleration is -14. 0 m/s 2 (upward) independent of motion direction. +x

Example 4: What is the maximum acceleration for the 2 -kg mass in the previous problem? (A = 12 cm, k = 400 N/m) The maximum acceleration occurs when the restoring force is a maximum; i. e. , when the stretch or compression of the spring is largest. F = ma = -kx xmax = A m Maximum Acceleration: amax = ± 24. 0 m/s 2 +x

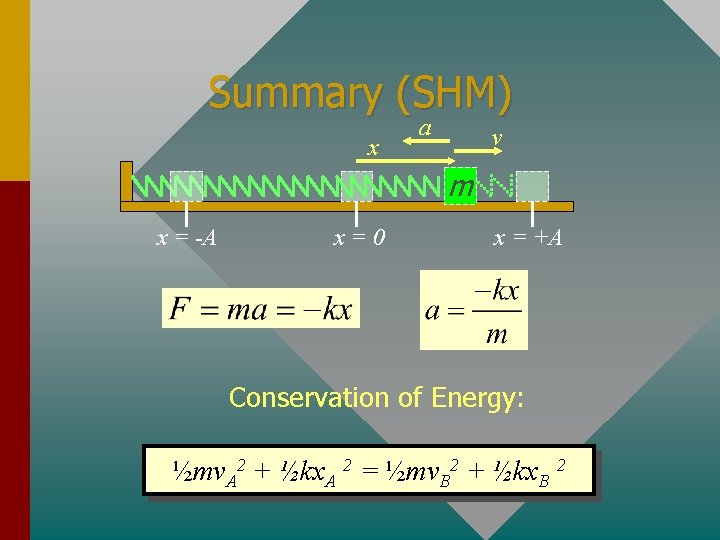
Conservation of Energy The total mechanical energy (U + K) of a vibrating system is constant; i. e. , it is the same at any point in the oscillating path. x a v m x = -A x=0 x = +A For any two points A and B, we may write: ½mv. A 2 + ½kx. A 2 = ½mv. B 2 + ½kx. B 2

Example 5 (Cont. ): What is the maximum velocity for the previous problem? (A = 10 cm, k = 800 N/m, m = 2 kg. ) The velocity is maximum when x = 0: 0 ½mv 2 + ½kx 2 = ½k. A 2 m v = ± 2. 00 m/s +x

The Period and Frequency as a Function of a and x. For any body undergoing simple harmonic motion: Since a = -4 p 2 f 2 x and T = 1/f The frequency and the period can be found if the displacement and acceleration are known. Note that the signs of a and x will always be opposite.

Period and Frequency as a Function of Mass and Spring Constant. For a vibrating body with an elastic restoring force: Recall that F = ma = -kx: -kx The frequency f and the period T can be found if the spring constant k and mass m of the vibrating body are known. Use consistent SI units.

Example 6: The frictionless system shown below has a 2 -kg mass attached to a spring (k = 400 N/m). The mass is displaced a distance of 20 cm to the right and released. What is the frequency of the motion? x a v m x = -0. 2 m x=0 f = 2. 25 Hz x = +0. 2 m

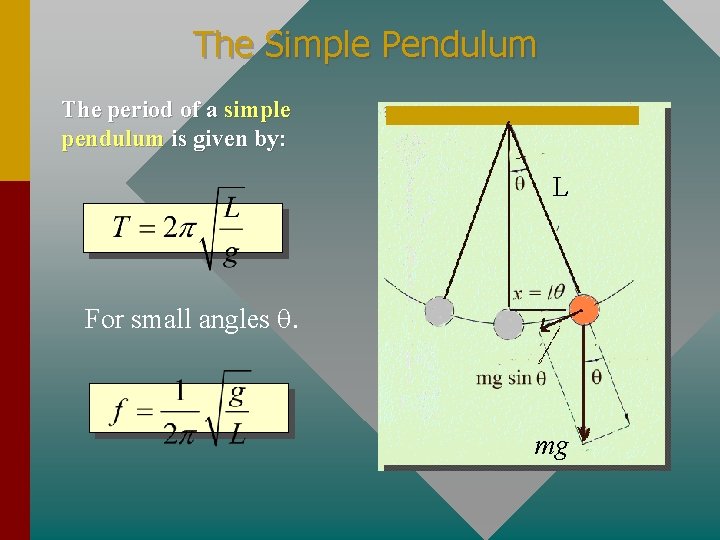
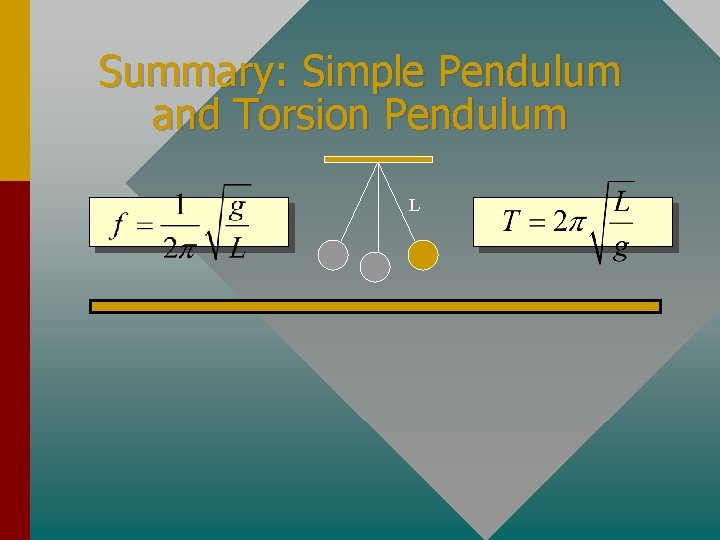
The Simple Pendulum The period of a simple pendulum is given by: L For small angles q. mg

Example 8. What must be the length of a simple pendulum for a clock which has a period of two seconds (tick-tock)? L L = 0. 993 m

The Torsion Pendulum The period T of a torsion pendulum is given by: Where k’ is a torsion constant that depends on the material from which the rod is made; I is the rotational inertia of the vibrating system.

Example 9: A 160 g solid disk is attached to the end of a wire, then twisted at 0. 8 rad and released. The torsion constant k’ is 0. 025 N m/rad. Find the period. (Neglect the torsion in the wire) For Disk: Disk I = ½m. R 2 I = ½(0. 16 kg)(0. 12 m)2 = 0. 00115 kg m 2 T = 1. 35 s Note: Period is independent of angular displacement.

Summary Simple harmonic motion (SHM) is that motion in which a body moves back and forth over a fixed path, returning to each position and velocity after a definite interval of time. The frequency (rev/s) is the reciprocal of the period (time for one revolution). x m F

Summary (Cont. ) Hooke’s Law: In a spring, there is a restoring force that is proportional to the displacement. x The spring constant k is defined by: m F

Summary (SHM) x a v m x = -A x=0 x = +A Conservation of Energy: ½mv. A 2 + ½kx. A 2 = ½mv. B 2 + ½kx. B 2

Summary: Simple Pendulum and Torsion Pendulum L

CONCLUSION Simple Harmonic Motion