Honors Track Competitive Programming Problem Solving PushRelabel Algorithm

Honors Track: Competitive Programming & Problem Solving Push-Relabel Algorithm Claire Claassen

Graph algorithms Structure p Max-flow problem p Recap augmenting path algorithms p Push relabel algorithm p Pseudocode p Example p Prove p Run-time

Max-flow problem Maximum flow problem Intuition: Given a network of pipes and a source and sink, how much water can be transported from source to sink?

Max-flow problem Bipartite graphs: Model relations between two classes of objects Examples n Boys and girls: “boy x likes girl y” A B
Max-flow problem Bipartite graphs: Model relations between two classes of objects Examples n Boys and girls: “boy x likes girl y” n Players and clubs: “player x wants to play in club y” A B
Max-flow problem Bipartite graphs: Model relations between two classes of objects Examples n Boys and girls: “boy x likes girl y” n Players and clubs: “player x wants to play in club y” n Employees and jobs: “employee x can perform job y” A B
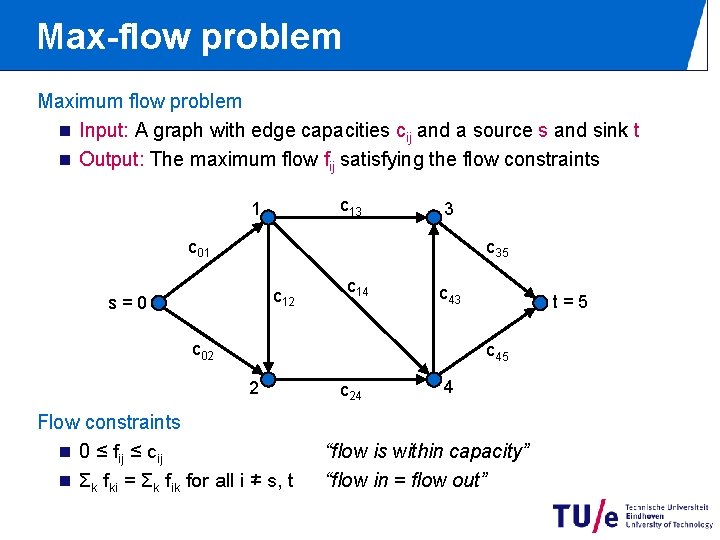
Max-flow problem Maximum flow problem n Input: A graph with edge capacities cij and a source s and sink t n Output: The maximum flow fij satisfying the flow constraints c 13 1 3 c 01 c 35 c 12 s=0 c 14 c 43 c 02 t=5 c 45 2 Flow constraints n 0 ≤ fij ≤ cij n Σk fki = Σk fik for all i ≠ s, t c 24 4 “flow is within capacity” “flow in = flow out”
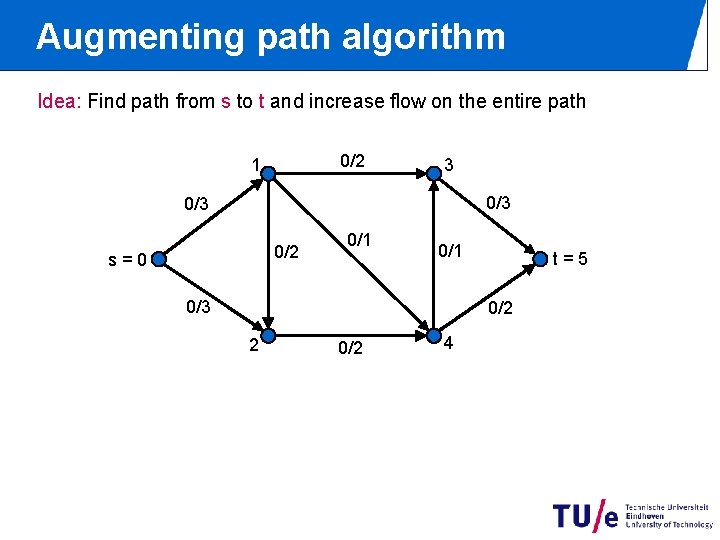
Augmenting path algorithm Idea: Find path from s to t and increase flow on the entire path 0/2 1 3 0/3 0/2 s=0 0/1 0/3 t=5 0/2 2 0/2 4
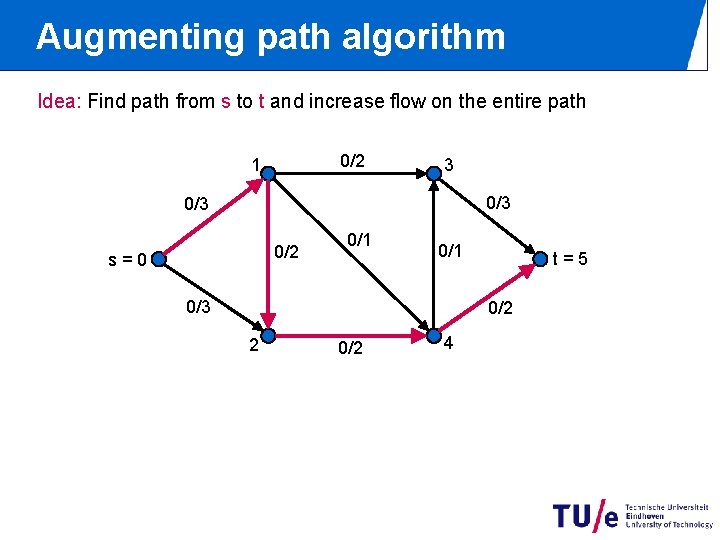
Augmenting path algorithm Idea: Find path from s to t and increase flow on the entire path 0/2 1 3 0/3 0/2 s=0 0/1 0/3 t=5 0/2 2 0/2 4
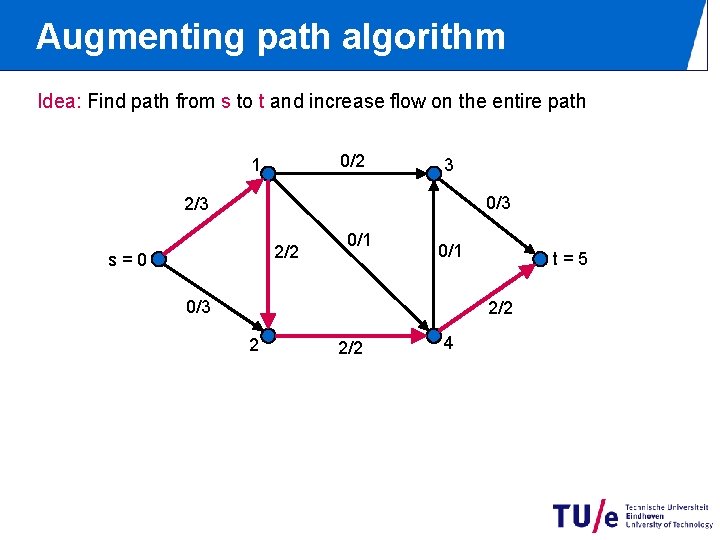
Augmenting path algorithm Idea: Find path from s to t and increase flow on the entire path 0/2 1 3 0/3 2/2 s=0 0/1 0/3 t=5 2/2 2 2/2 4
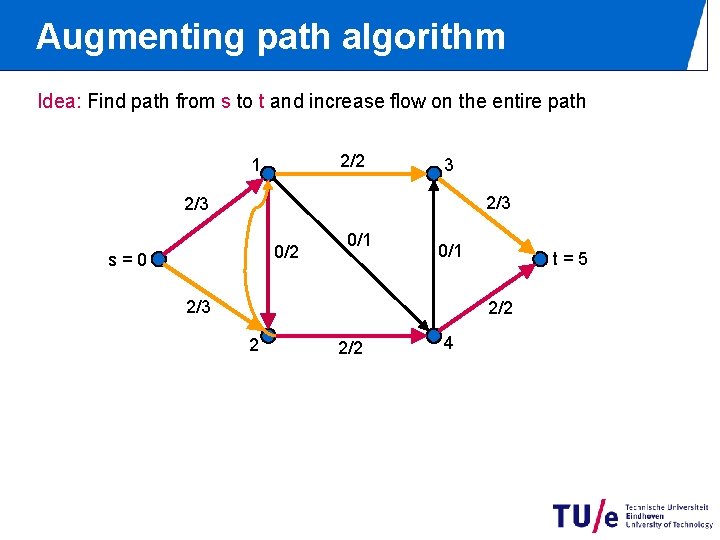
Augmenting path algorithm Idea: Find path from s to t and increase flow on the entire path 2/2 1 3 2/3 0/2 s=0 0/1 2/3 t=5 2/2 2 2/2 4
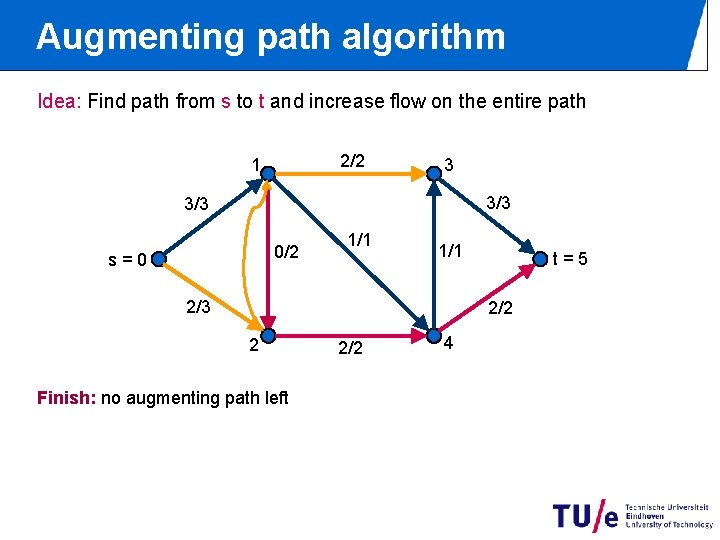
Augmenting path algorithm Idea: Find path from s to t and increase flow on the entire path 2/2 1 3 3/3 0/2 s=0 1/1 2/3 t=5 2/2 2 Finish: no augmenting path left 2/2 4

Max-Flow idea General idea: p The flow is optimal if there’s no path between s and t Graph approach: p DFS ➨ Ford-Fulkerson algorithm with O(E f*) running time p BFS ➨ Edmonds-Karp algorithm with O(V E 2) running time Without searching for path p Push-relabel algorithm ➨ O(V 2 E)

Push-relabel approach p
![Pseudocode Pseudo-code: p h[s] = |V| p For each v ϵ V – {s} Pseudocode Pseudo-code: p h[s] = |V| p For each v ϵ V – {s}](http://slidetodoc.com/presentation_image_h2/5198ba68ce3088b9e233e194efcb8477/image-15.jpg)
Pseudocode Pseudo-code: p h[s] = |V| p For each v ϵ V – {s} do h[v] = 0 p For each (s, v) ϵ E do f(s, v) = c(s, v) p While f is not feasible flow n If there’s a vertex v ϵ V – {s, t} and a vertex w ϵ V with e(v) > 0 and h[v] > h[w] and c’(v, w) > 0 p Push min(c’(v, w), e(v)) over edge (v, w) p Else h[v] = h[v] +1
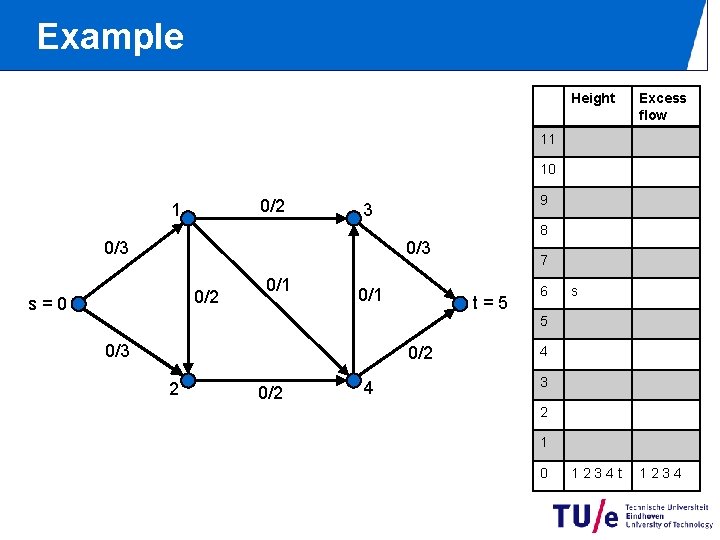
Example Height Excess flow 11 10 0/2 1 9 3 8 0/3 0/2 s=0 0/1 7 t=5 6 s 5 0/3 0/2 2 0/2 4 4 3 2 1 0 1234 t 1234
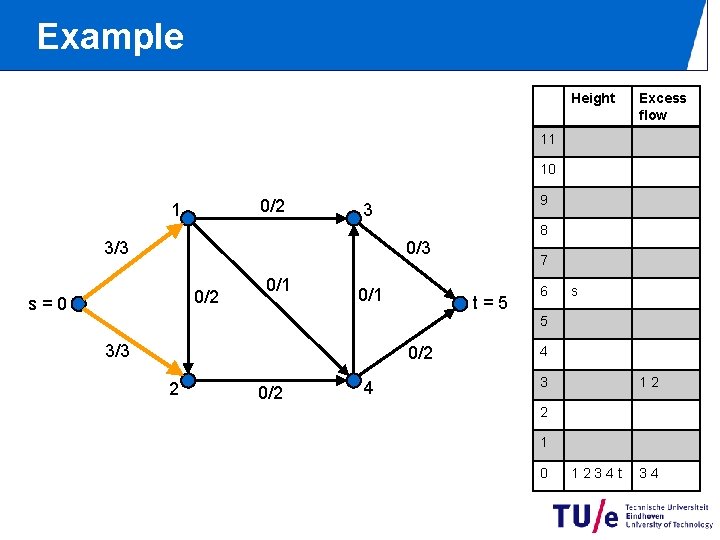
Example Height Excess flow 11 10 0/2 1 9 3 8 0/3 3/3 0/2 s=0 0/1 7 t=5 6 s 5 3/3 0/2 2 0/2 4 4 3 12 2 1 0 1234 t 34
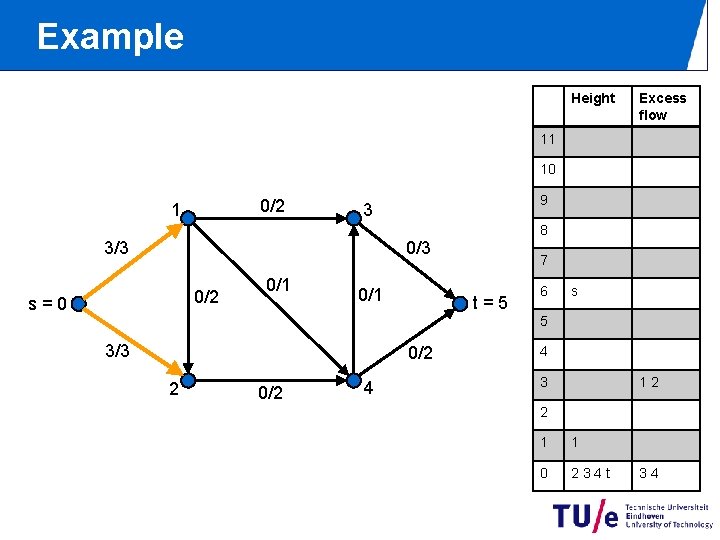
Example Height Excess flow 11 10 0/2 1 9 3 8 0/3 3/3 0/2 s=0 0/1 7 t=5 6 s 5 3/3 0/2 2 0/2 4 4 3 12 2 1 1 0 234 t 34
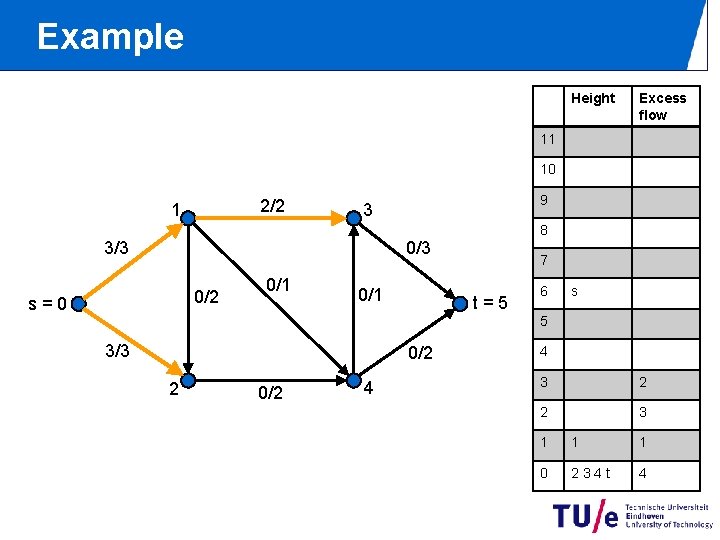
Example Height Excess flow 11 10 2/2 1 9 3 8 0/3 3/3 0/2 s=0 0/1 7 t=5 6 s 5 3/3 0/2 2 0/2 4 4 3 2 2 3 1 1 1 0 234 t 4
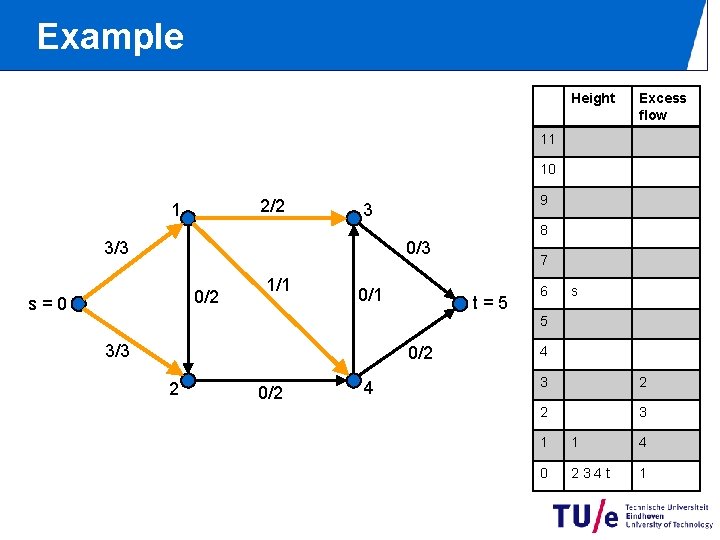
Example Height Excess flow 11 10 2/2 1 9 3 8 0/3 3/3 0/2 s=0 1/1 0/1 7 t=5 6 s 5 3/3 0/2 2 0/2 4 4 3 2 2 3 1 1 4 0 234 t 1
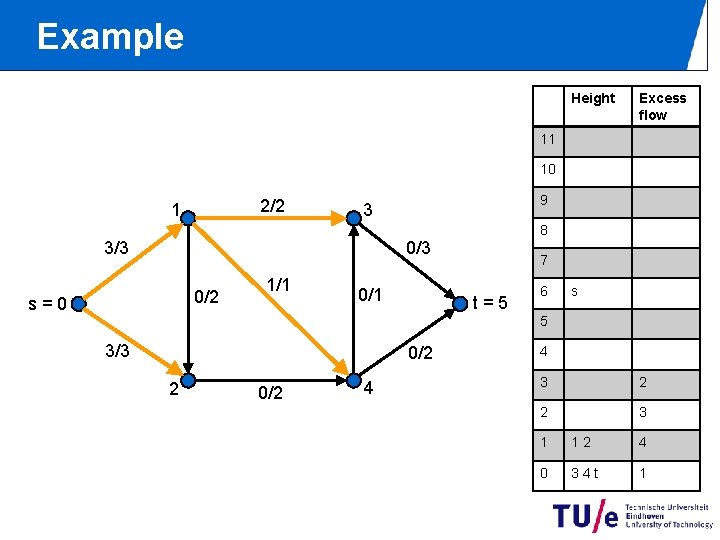
Example Height Excess flow 11 10 2/2 1 9 3 8 0/3 3/3 0/2 s=0 1/1 0/1 7 t=5 6 s 5 3/3 0/2 2 0/2 4 4 3 2 2 3 1 12 4 0 34 t 1
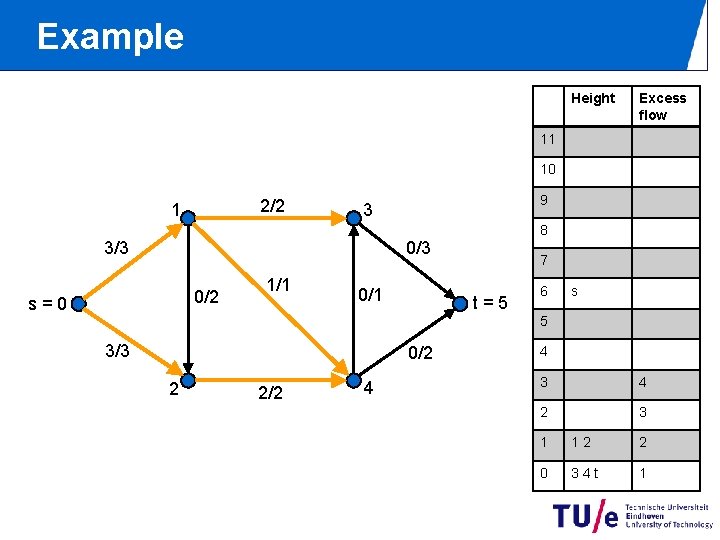
Example Height Excess flow 11 10 2/2 1 9 3 8 0/3 3/3 0/2 s=0 1/1 0/1 7 t=5 6 s 5 3/3 0/2 2 2/2 4 4 3 4 2 3 1 12 2 0 34 t 1
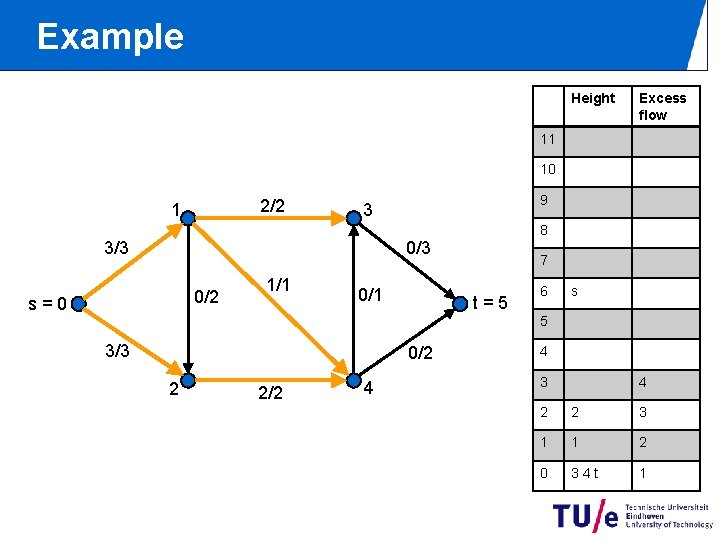
Example Height Excess flow 11 10 2/2 1 9 3 8 0/3 3/3 0/2 s=0 1/1 0/1 7 t=5 6 s 5 3/3 0/2 2 2/2 4 4 3 4 2 2 3 1 1 2 0 34 t 1
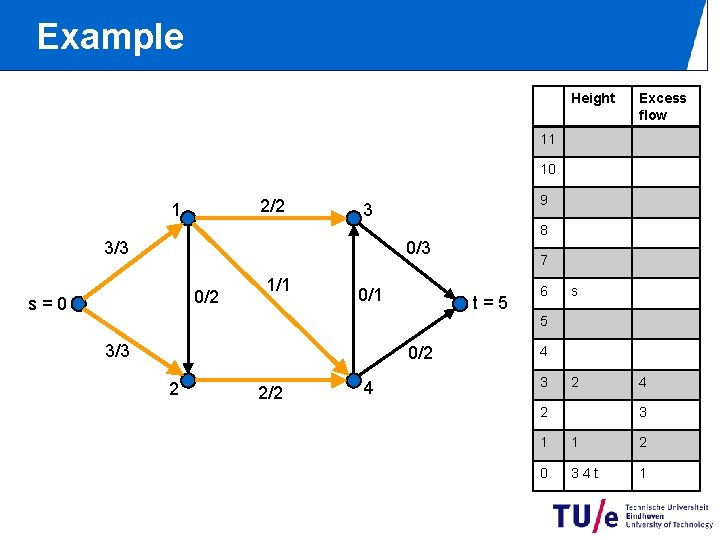
Example Height Excess flow 11 10 2/2 1 9 3 8 0/3 3/3 0/2 s=0 1/1 0/1 7 t=5 6 s 5 3/3 0/2 2 2/2 4 4 3 2 2 4 3 1 1 2 0 34 t 1
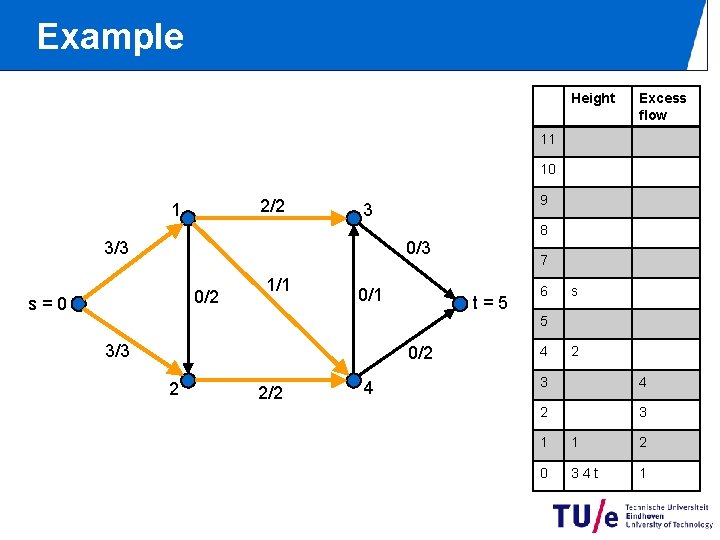
Example Height Excess flow 11 10 2/2 1 9 3 8 0/3 3/3 0/2 s=0 1/1 0/1 7 t=5 6 s 5 3/3 0/2 2 2/2 4 4 2 3 1 1 2 0 34 t 1
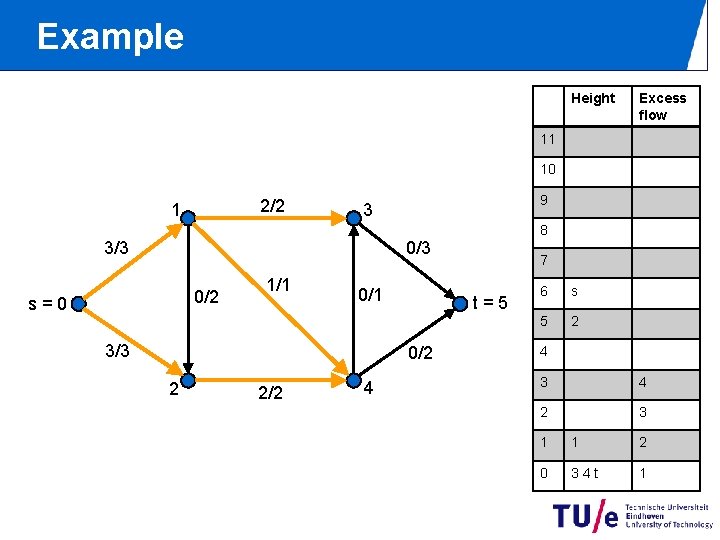
Example Height Excess flow 11 10 2/2 1 9 3 8 0/3 3/3 0/2 s=0 1/1 0/1 3/3 t=5 0/2 2 2/2 4 7 6 s 5 2 4 3 4 2 3 1 1 2 0 34 t 1
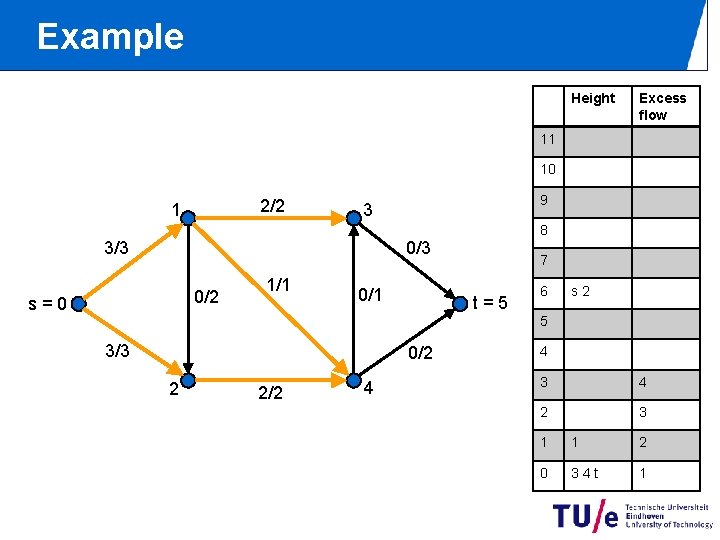
Example Height Excess flow 11 10 2/2 1 9 3 8 0/3 3/3 0/2 s=0 1/1 0/1 7 t=5 6 s 2 5 3/3 0/2 2 2/2 4 4 3 4 2 3 1 1 2 0 34 t 1
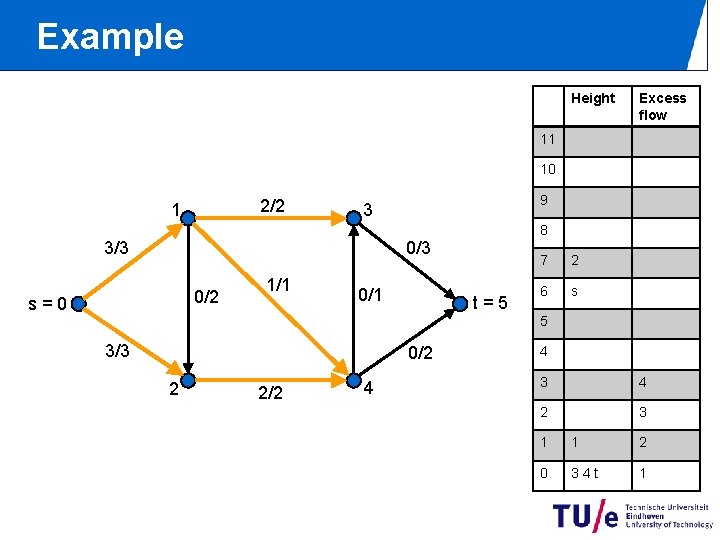
Example Height Excess flow 11 10 2/2 1 9 3 8 0/3 3/3 0/2 s=0 1/1 0/1 t=5 7 2 6 s 5 3/3 0/2 2 2/2 4 4 3 4 2 3 1 1 2 0 34 t 1
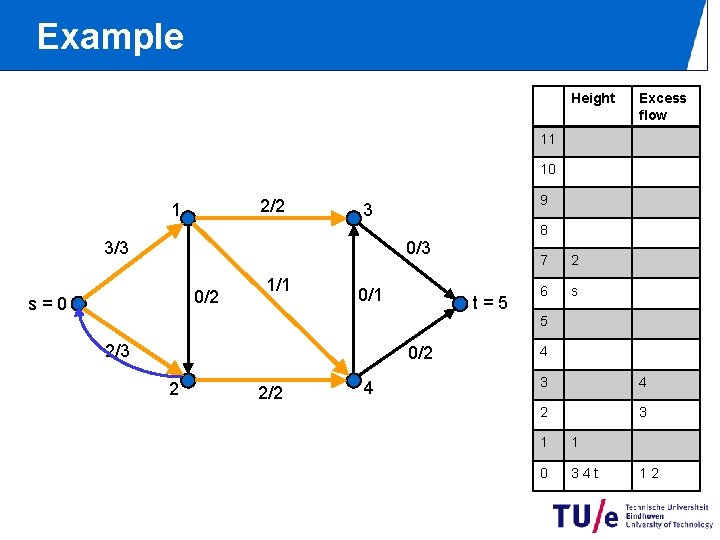
Example Height Excess flow 11 10 2/2 1 9 3 8 0/3 3/3 0/2 s=0 1/1 0/1 t=5 7 2 6 s 5 2/3 0/2 2 2/2 4 4 3 4 2 3 1 1 0 34 t 12
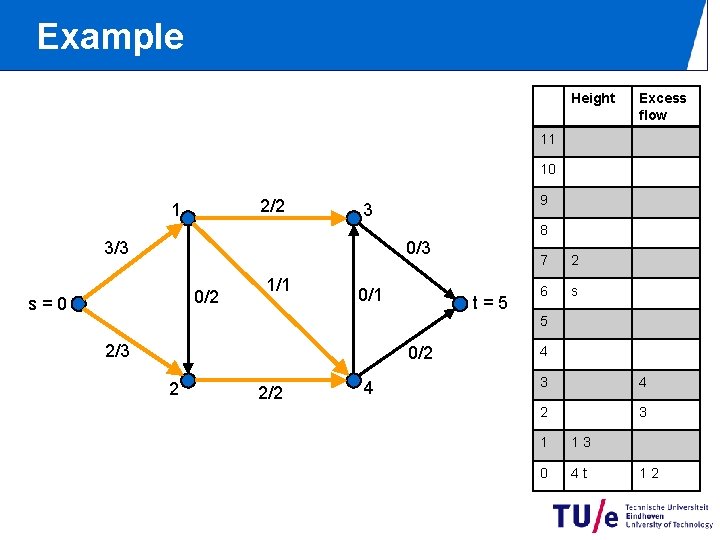
Example Height Excess flow 11 10 2/2 1 9 3 8 0/3 3/3 0/2 s=0 1/1 0/1 t=5 7 2 6 s 5 2/3 0/2 2 2/2 4 4 3 4 2 3 1 13 0 4 t 12
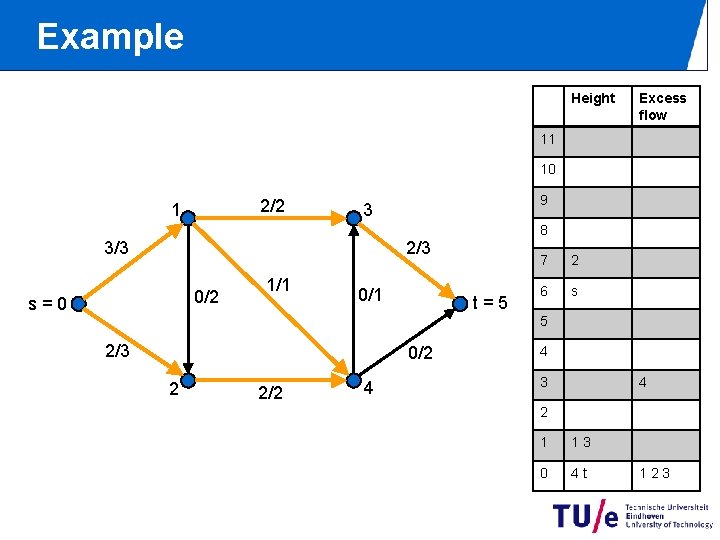
Example Height Excess flow 11 10 2/2 1 9 3 8 2/3 3/3 0/2 s=0 1/1 0/1 t=5 7 2 6 s 5 2/3 0/2 2 2/2 4 4 3 4 2 1 13 0 4 t 123
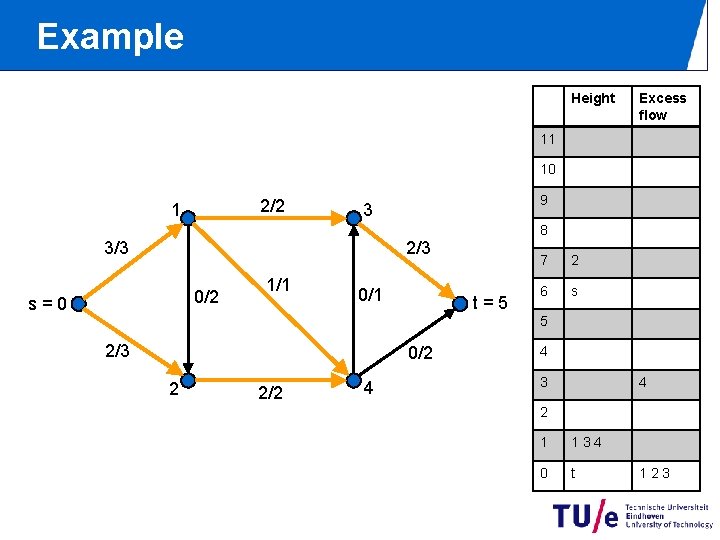
Example Height Excess flow 11 10 2/2 1 9 3 8 2/3 3/3 0/2 s=0 1/1 0/1 t=5 7 2 6 s 5 2/3 0/2 2 2/2 4 4 3 4 2 1 134 0 t 123
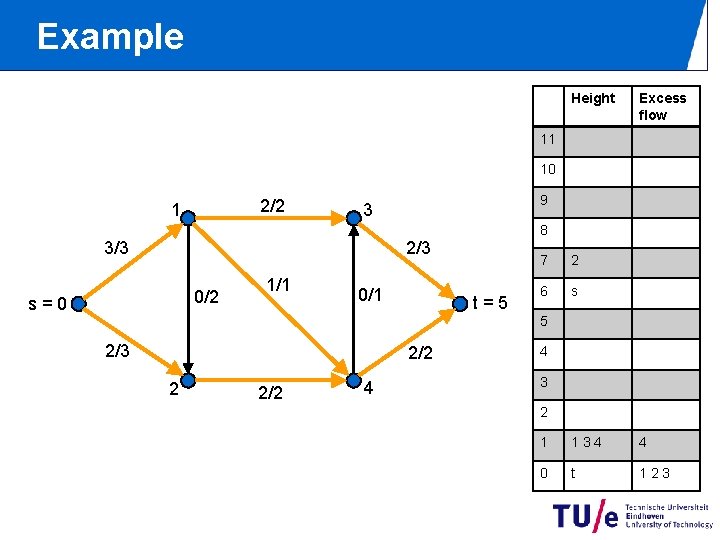
Example Height Excess flow 11 10 2/2 1 9 3 8 2/3 3/3 0/2 s=0 1/1 0/1 t=5 7 2 6 s 5 2/3 2/2 2 2/2 4 4 3 2 1 134 4 0 t 123
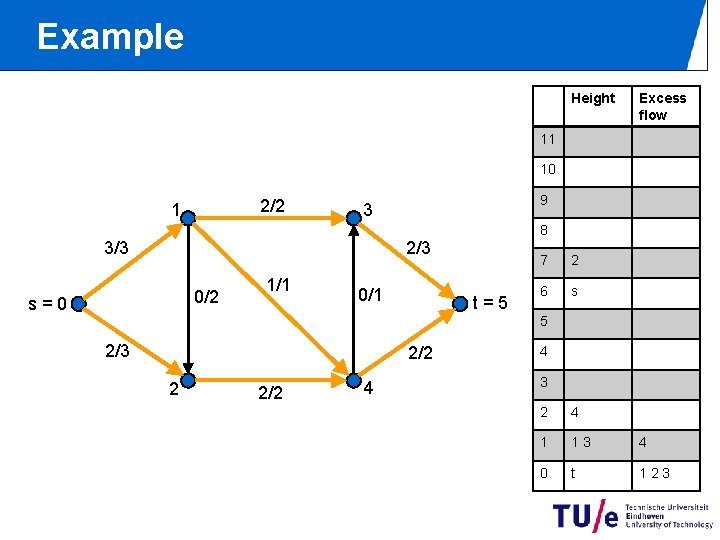
Example Height Excess flow 11 10 2/2 1 9 3 8 2/3 3/3 0/2 s=0 1/1 0/1 t=5 7 2 6 s 5 2/3 2/2 2 2/2 4 4 3 2 4 1 13 4 0 t 123
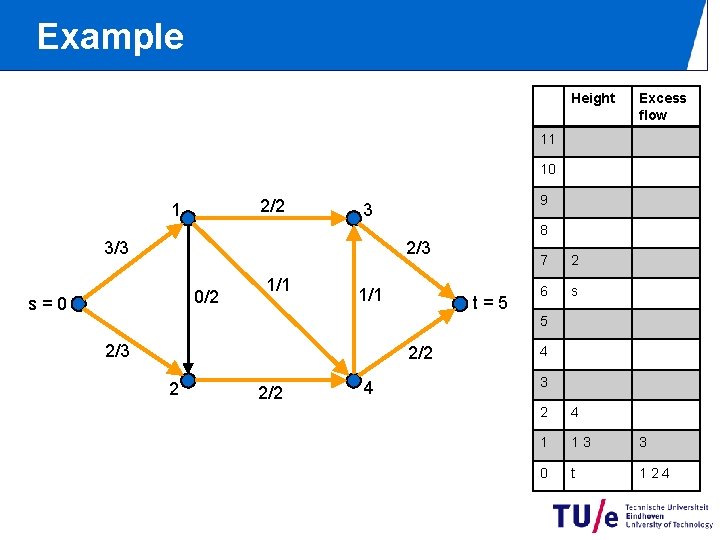
Example Height Excess flow 11 10 2/2 1 9 3 8 2/3 3/3 0/2 s=0 1/1 t=5 7 2 6 s 5 2/3 2/2 2 2/2 4 4 3 2 4 1 13 3 0 t 124
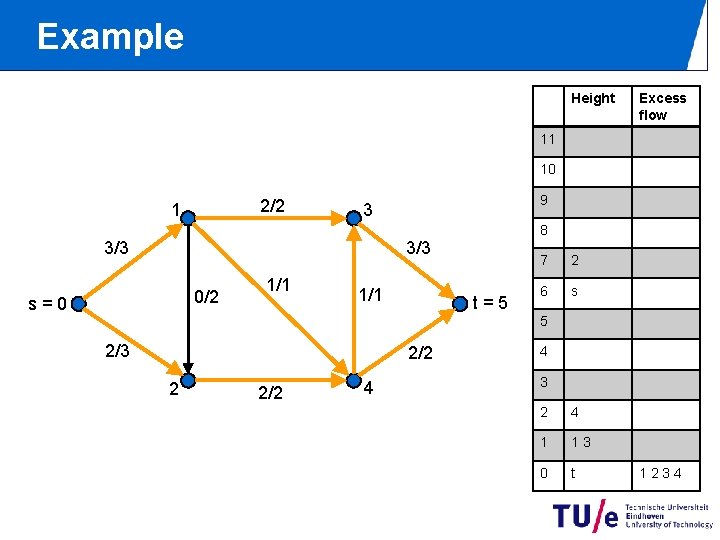
Example Height Excess flow 11 10 2/2 1 9 3 8 3/3 0/2 s=0 1/1 t=5 7 2 6 s 5 2/3 2/2 2 2/2 4 4 3 2 4 1 13 0 t 1234
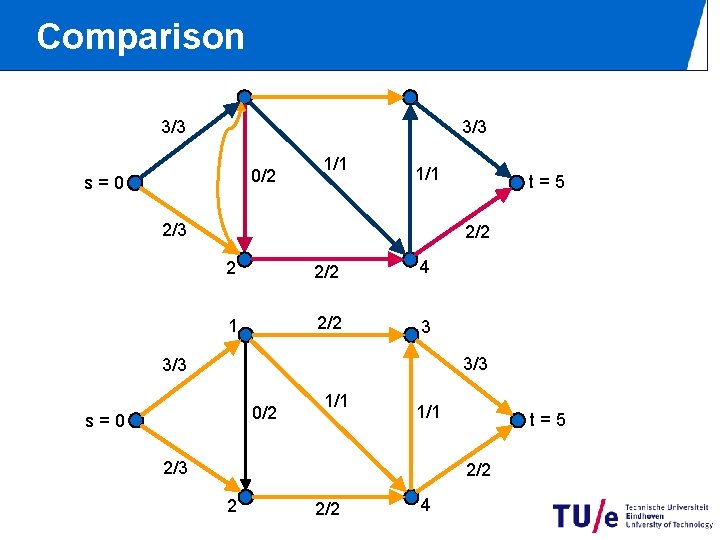
Comparison 3/3 0/2 s=0 1/1 2/3 t=5 2/2 2 2/2 4 1 2/2 3 3/3 0/2 s=0 1/1 2/3 t=5 2/2 2 2/2 4

Prove p 3/3 1 t=3 0/2 s=0 0/1 2 Node Excess flow 0 -3 1 3 2 0 3 0
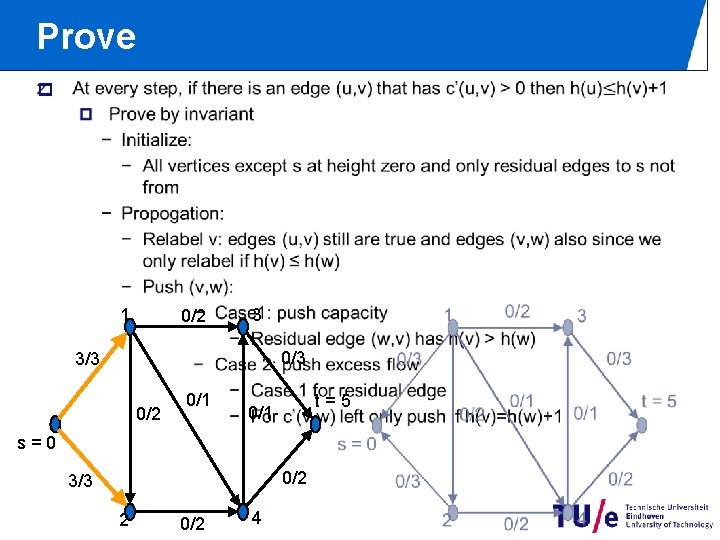
Prove p 1 0/2 3 0/3 3/3 0/2 0/1 t=5 0/1 s=0 0/2 3/3 2 0/2 4

Prove p 0 1 2

Run time p

Run time 2 p
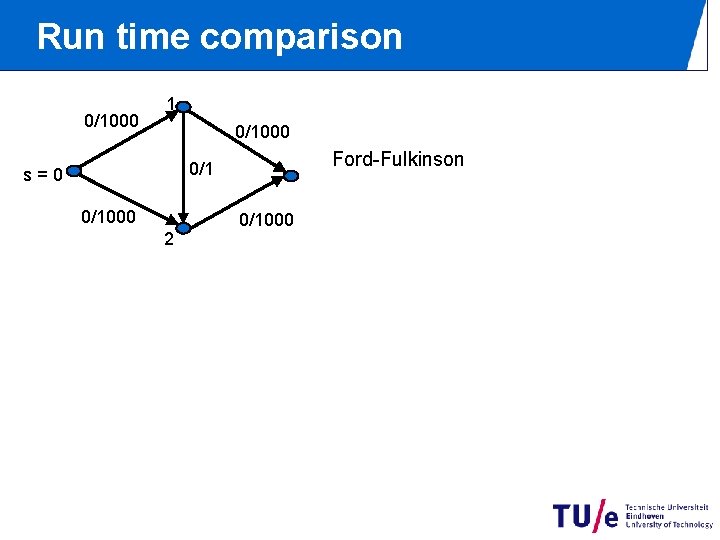
Run time comparison 0/1000 1 0/1000 Ford-Fulkinson 0/1 s=0 0/1000 2 0/1000
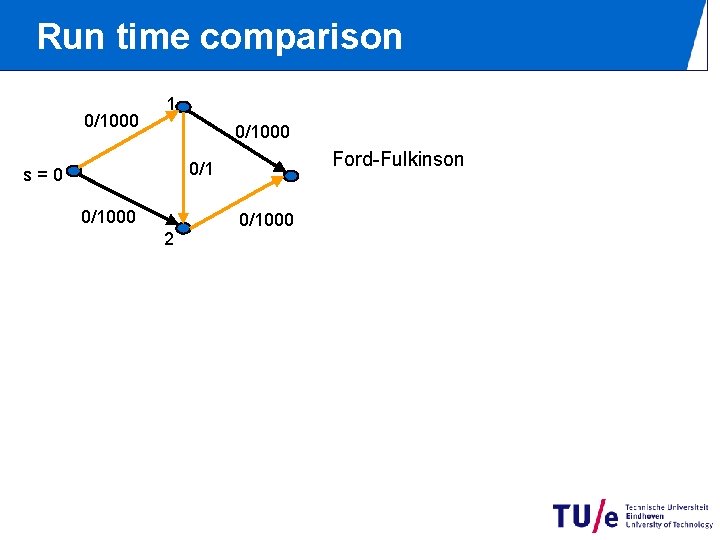
Run time comparison 0/1000 1 0/1000 Ford-Fulkinson 0/1 s=0 0/1000 2 0/1000
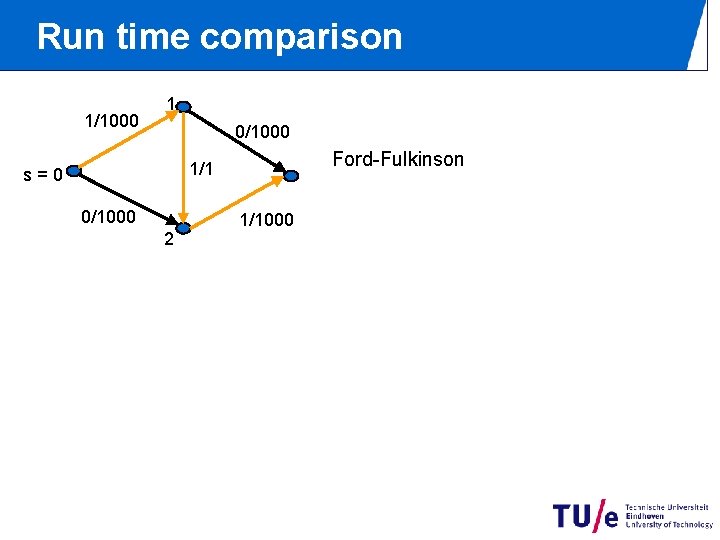
Run time comparison 1/1000 1 0/1000 Ford-Fulkinson 1/1 s=0 0/1000 2 1/1000
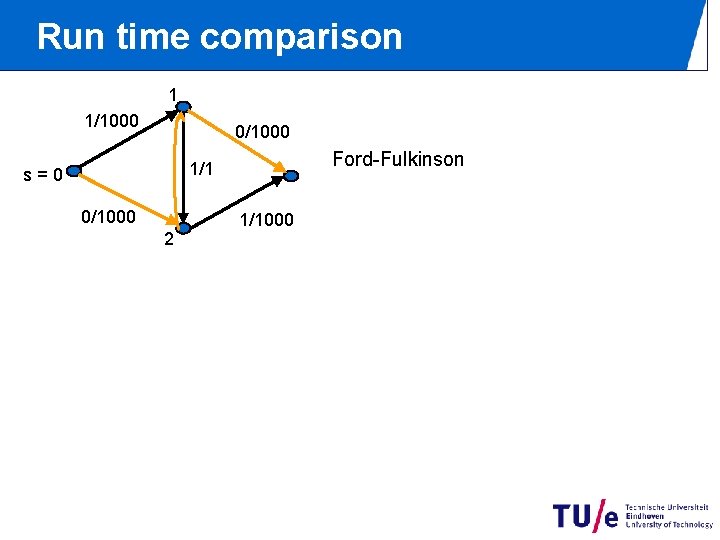
Run time comparison 1 1/1000 0/1000 Ford-Fulkinson 1/1 s=0 0/1000 2 1/1000
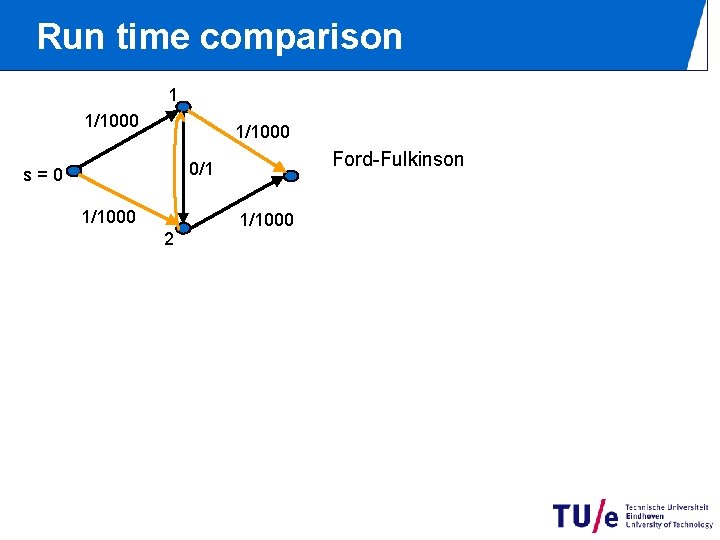
Run time comparison 1 1/1000 Ford-Fulkinson 0/1 s=0 1/1000 2 1/1000
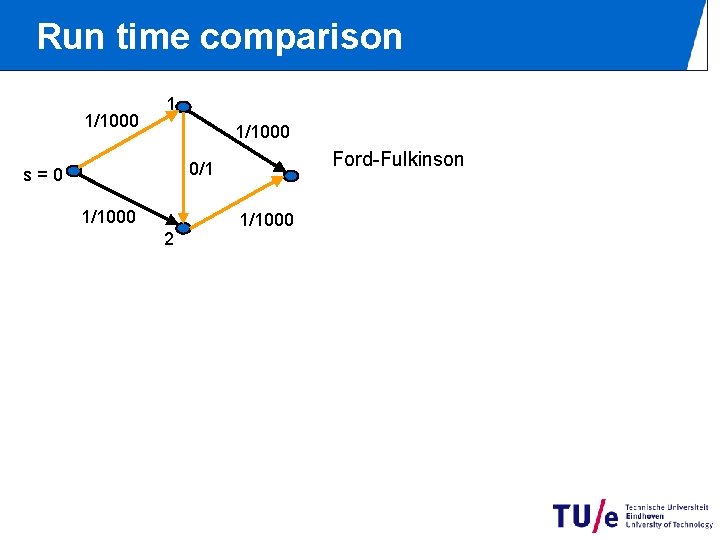
Run time comparison 1/1000 1 1/1000 Ford-Fulkinson 0/1 s=0 1/1000 2 1/1000
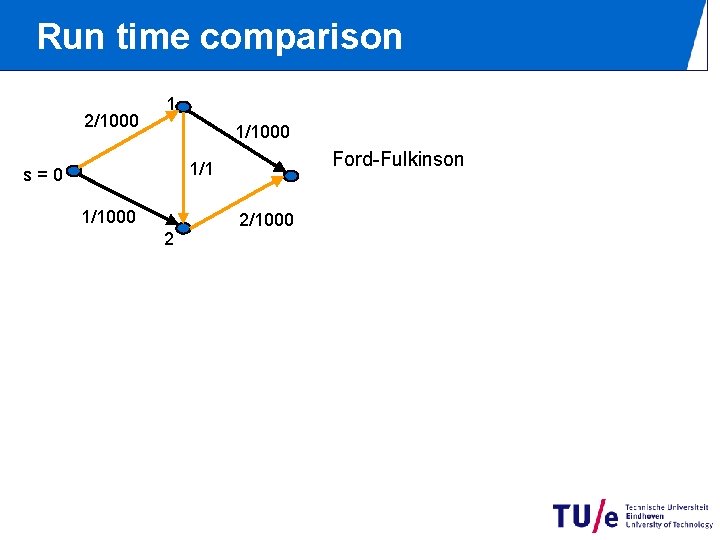
Run time comparison 2/1000 1 1/1000 Ford-Fulkinson 1/1 s=0 1/1000 2 2/1000
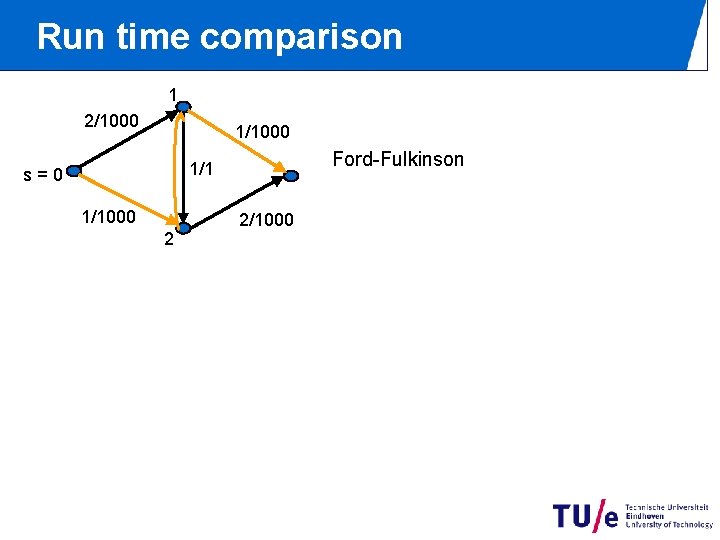
Run time comparison 1 2/1000 1/1000 Ford-Fulkinson 1/1 s=0 1/1000 2 2/1000
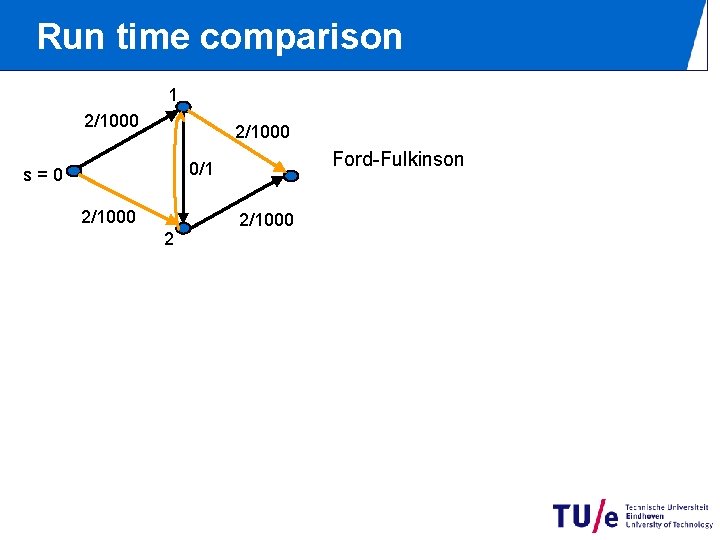
Run time comparison 1 2/1000 Ford-Fulkinson 0/1 s=0 2/1000 2 2/1000
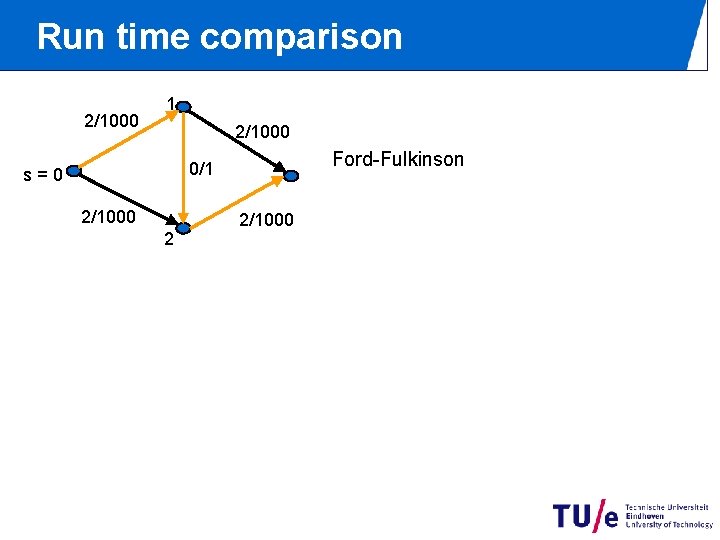
Run time comparison 2/1000 1 2/1000 Ford-Fulkinson 0/1 s=0 2/1000 2 2/1000
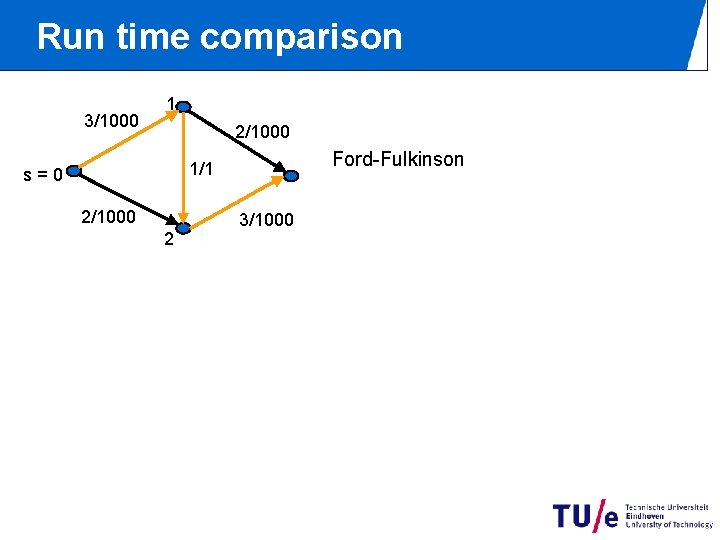
Run time comparison 3/1000 1 2/1000 Ford-Fulkinson 1/1 s=0 2/1000 2 3/1000
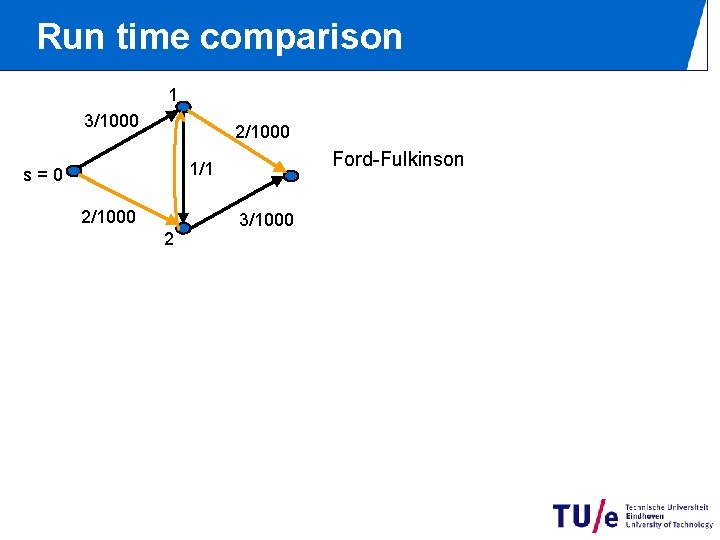
Run time comparison 1 3/1000 2/1000 Ford-Fulkinson 1/1 s=0 2/1000 2 3/1000
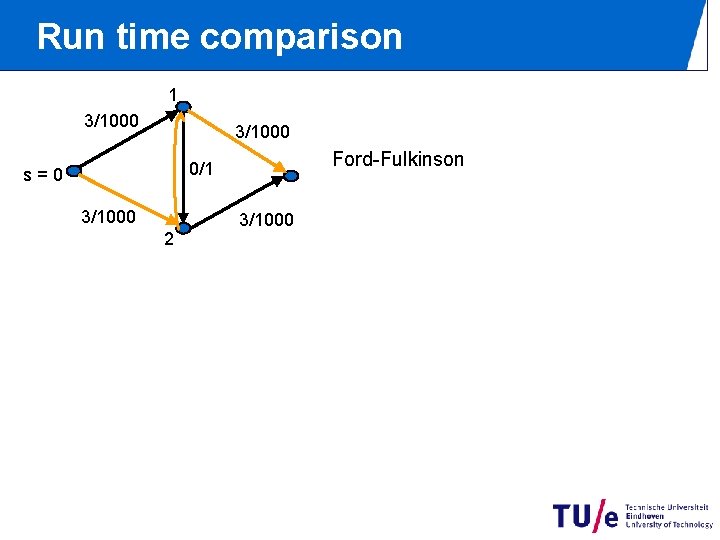
Run time comparison 1 3/1000 Ford-Fulkinson 0/1 s=0 3/1000 2 3/1000
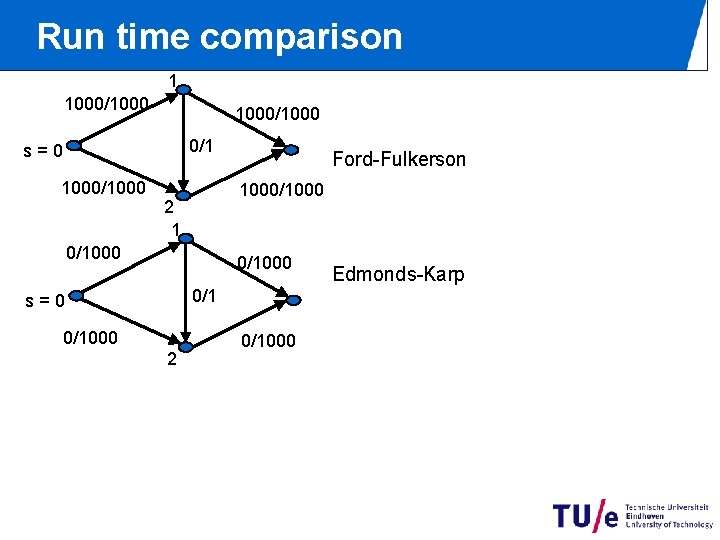
Run time comparison 1 1000/1000 0/1 s=0 1000/1000 Ford-Fulkerson 1000/1000 2 1 0/1000 0/1 s=0 0/1000 2 0/1000 Edmonds-Karp
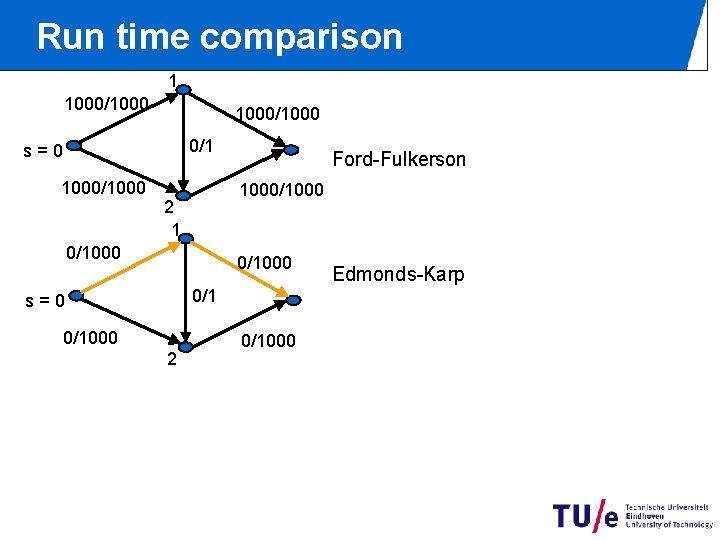
Run time comparison 1 1000/1000 0/1 s=0 1000/1000 Ford-Fulkerson 1000/1000 2 1 0/1000 0/1 s=0 0/1000 2 0/1000 Edmonds-Karp
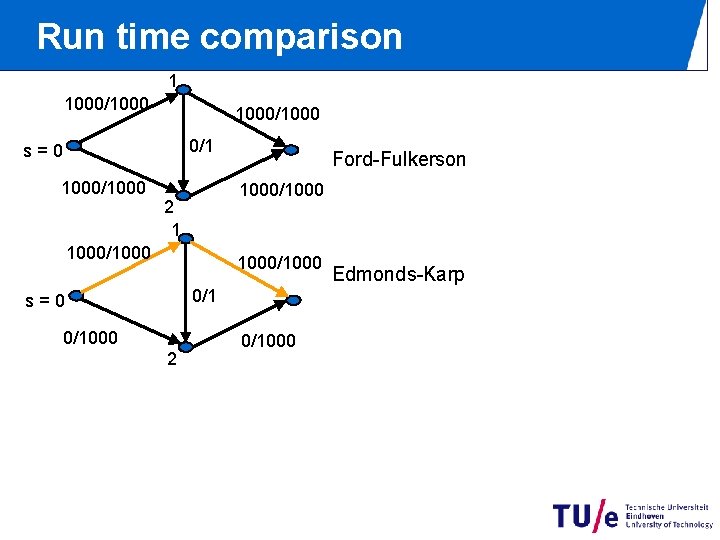
Run time comparison 1 1000/1000 0/1 s=0 1000/1000 Ford-Fulkerson 1000/1000 2 1 1000/1000 0/1 s=0 0/1000 2 0/1000 Edmonds-Karp
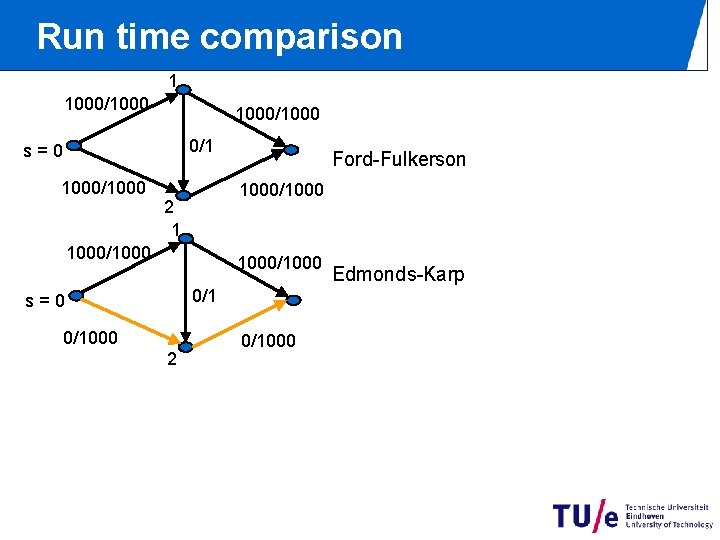
Run time comparison 1 1000/1000 0/1 s=0 1000/1000 Ford-Fulkerson 1000/1000 2 1 1000/1000 0/1 s=0 0/1000 2 0/1000 Edmonds-Karp
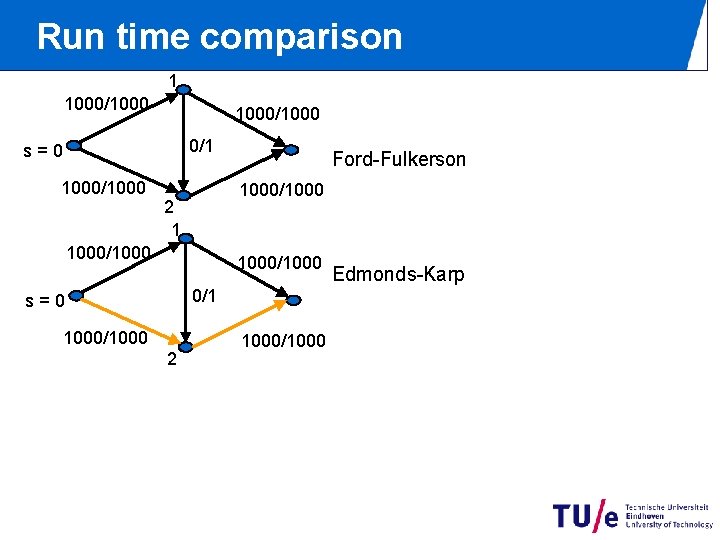
Run time comparison 1 1000/1000 0/1 s=0 1000/1000 Ford-Fulkerson 1000/1000 2 1 1000/1000 0/1 s=0 1000/1000 2 1000/1000 Edmonds-Karp
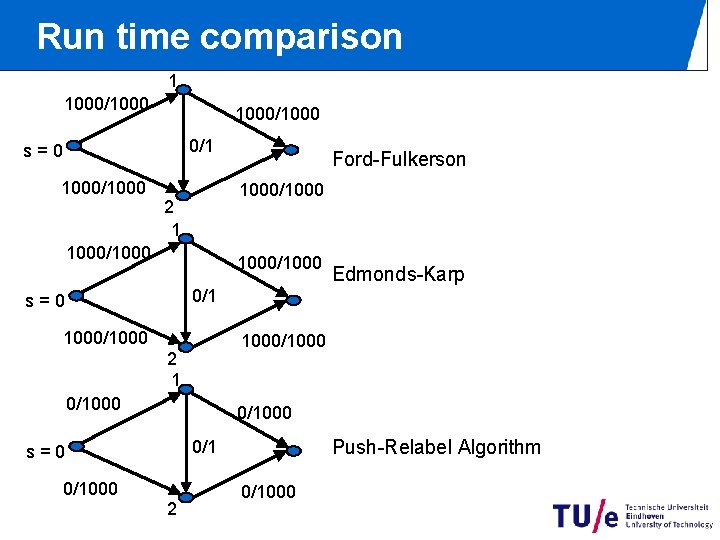
Run time comparison 1 1000/1000 0/1 s=0 1000/1000 Ford-Fulkerson 1000/1000 2 1 1000/1000 Edmonds-Karp 0/1 s=0 1000/1000 2 1 0/1000 Push-Relabel Algorithm 0/1 s=0 0/1000 2 0/1000
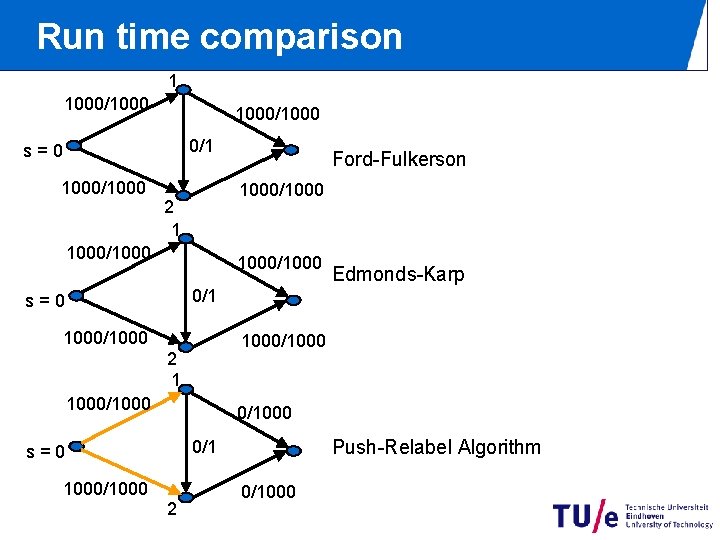
Run time comparison 1 1000/1000 0/1 s=0 1000/1000 Ford-Fulkerson 1000/1000 2 1 1000/1000 Edmonds-Karp 0/1 s=0 1000/1000 2 1 1000/1000 Push-Relabel Algorithm 0/1 s=0 1000/1000 2 0/1000
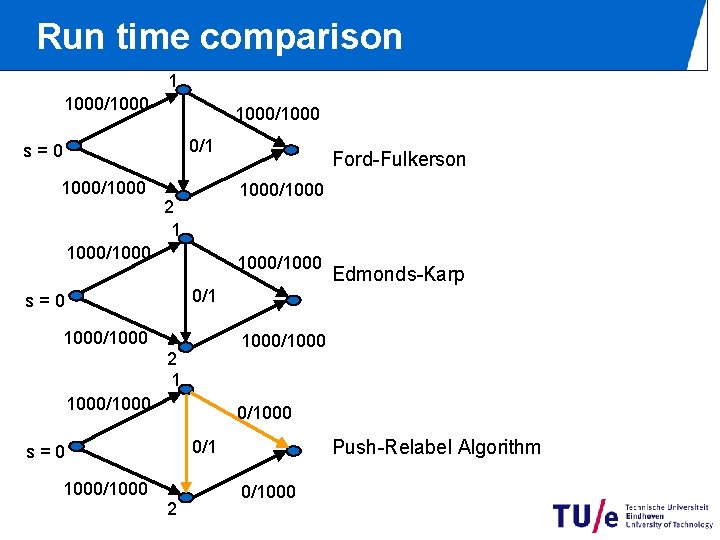
Run time comparison 1 1000/1000 0/1 s=0 1000/1000 Ford-Fulkerson 1000/1000 2 1 1000/1000 Edmonds-Karp 0/1 s=0 1000/1000 2 1 1000/1000 Push-Relabel Algorithm 0/1 s=0 1000/1000 2 0/1000
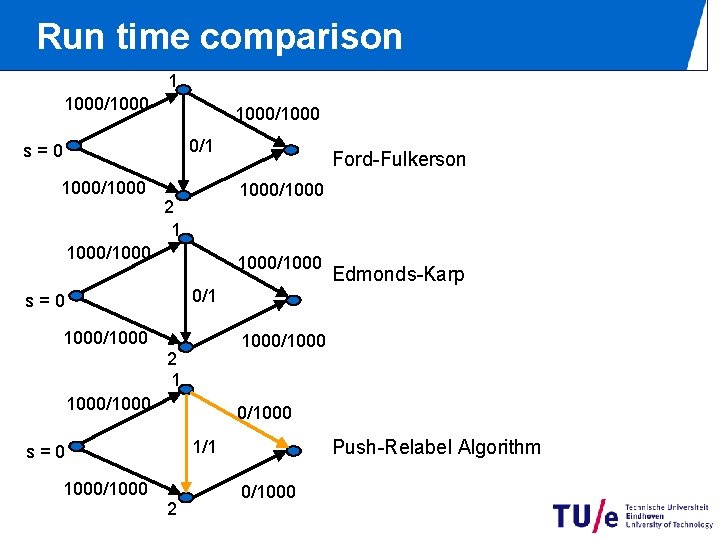
Run time comparison 1 1000/1000 0/1 s=0 1000/1000 Ford-Fulkerson 1000/1000 2 1 1000/1000 Edmonds-Karp 0/1 s=0 1000/1000 2 1 1000/1000 Push-Relabel Algorithm 1/1 s=0 1000/1000 2 0/1000
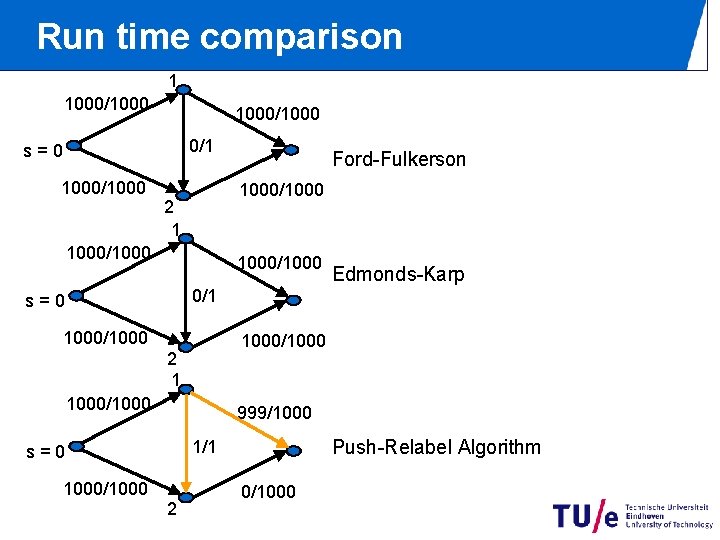
Run time comparison 1 1000/1000 0/1 s=0 1000/1000 Ford-Fulkerson 1000/1000 2 1 1000/1000 Edmonds-Karp 0/1 s=0 1000/1000 2 1 1000/1000 999/1000 Push-Relabel Algorithm 1/1 s=0 1000/1000 2 0/1000
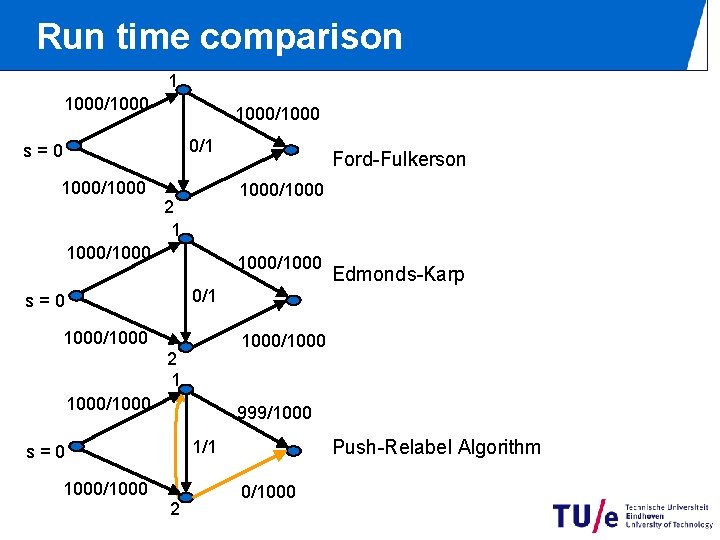
Run time comparison 1 1000/1000 0/1 s=0 1000/1000 Ford-Fulkerson 1000/1000 2 1 1000/1000 Edmonds-Karp 0/1 s=0 1000/1000 2 1 1000/1000 999/1000/1000 Push-Relabel Algorithm 1/1 s=0 2 0/1000
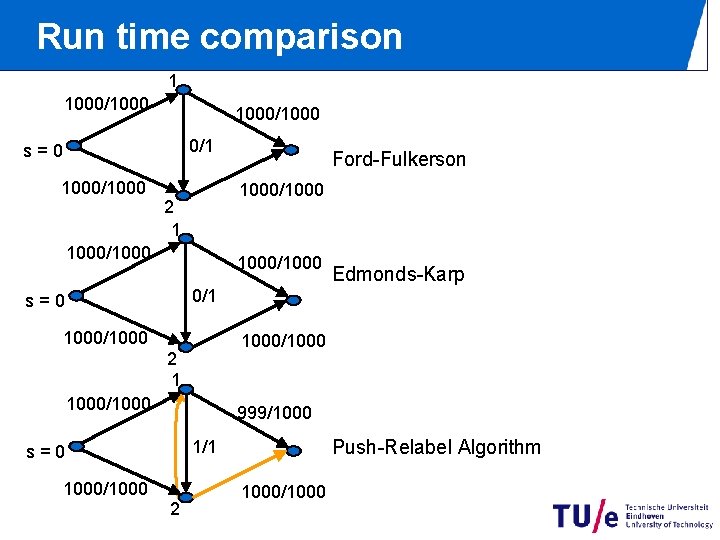
Run time comparison 1 1000/1000 0/1 s=0 1000/1000 Ford-Fulkerson 1000/1000 2 1 1000/1000 Edmonds-Karp 0/1 s=0 1000/1000 2 1 1000/1000 999/1000/1000 Push-Relabel Algorithm 1/1 s=0 2 1000/1000

Run time comparison 1 1000/1000 0/1 s=0 1000/1000 Ford-Fulkerson 1000/1000 2 1 1000/1000 Edmonds-Karp 0/1 s=0 1000/1000 2 1 1000/1000 999/1000/1000 Push-Relabel Algorithm 0/1 s=0 2 1000/1000
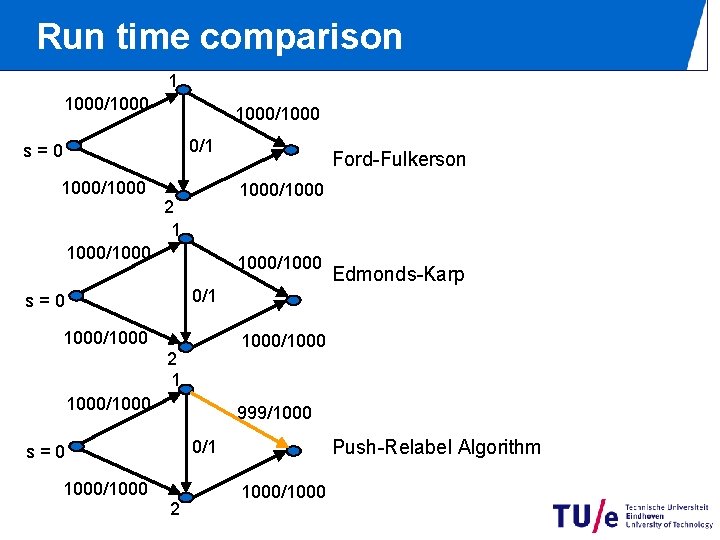
Run time comparison 1 1000/1000 0/1 s=0 1000/1000 Ford-Fulkerson 1000/1000 2 1 1000/1000 Edmonds-Karp 0/1 s=0 1000/1000 2 1 1000/1000 999/1000/1000 Push-Relabel Algorithm 0/1 s=0 2 1000/1000
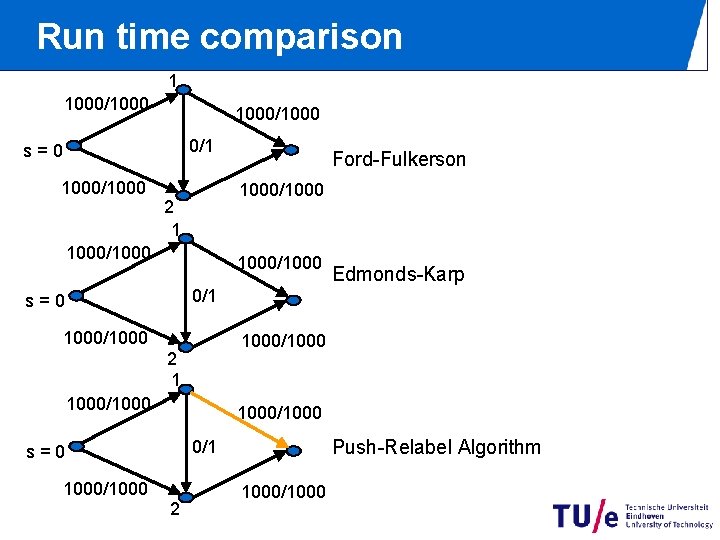
Run time comparison 1 1000/1000 0/1 s=0 1000/1000 Ford-Fulkerson 1000/1000 2 1 1000/1000 Edmonds-Karp 0/1 s=0 1000/1000 2 1 1000/1000 Push-Relabel Algorithm 0/1 s=0 2 1000/1000

Run time comparison 1 1000/1000 0/1 s=0 1000/1000 Ford-Fulkerson 1000/1000 2 1 1000/1000 Edmonds-Karp 0/1 s=0 1000/1000 2 1 1000/1000 Push-Relabel Algorithm 0/1 s=0 2 1000/1000

Run time comparison 1 1000/1000 0/1 s=0 1000/1000 2 1 1000/1000 0/1 s=0 1000/1000 2 1000/1000 p

- Slides: 73