Honors Systems Solving a System Getting the ordered

Honors Systems

Solving a System Getting the ordered pair that makes both equations true Where the two lines would intersect You could have: No solution – meaning they never intersect 1 solution they intersect once Infinite solutions – they are really the same line

Graphically 1. Solve both equations for y, get in the form y=mx+b 2. Graph both of the lines (we have discussed a few ways to do this, listed below is one of them) a. Plot y-int b. Do slope from y-int c. Connect with a line 3. Find point of intersection This works well if lines intersect at an exact point 4. Check to see if point works in both equations

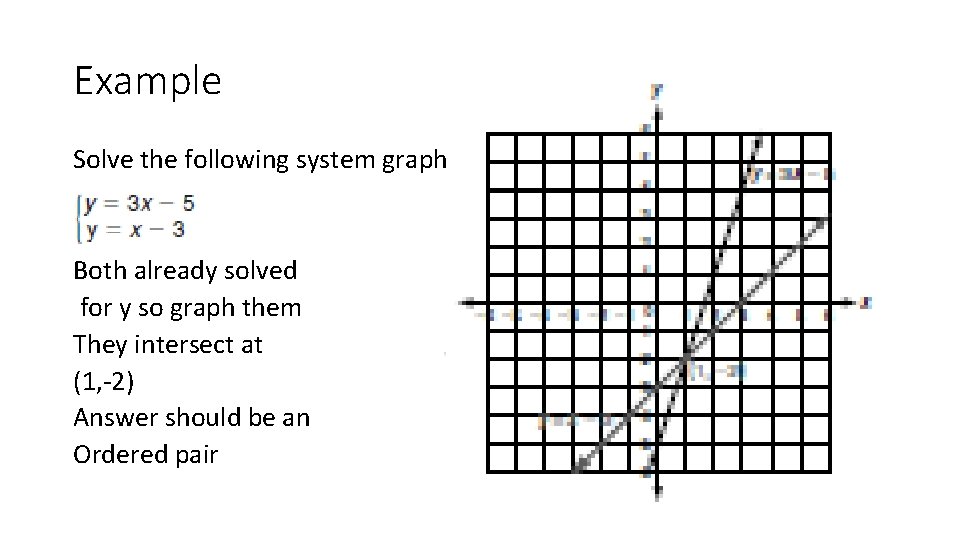
Example Solve the following system graphically Both already solved for y so graph them They intersect at (1, -2) Answer should be an Ordered pair

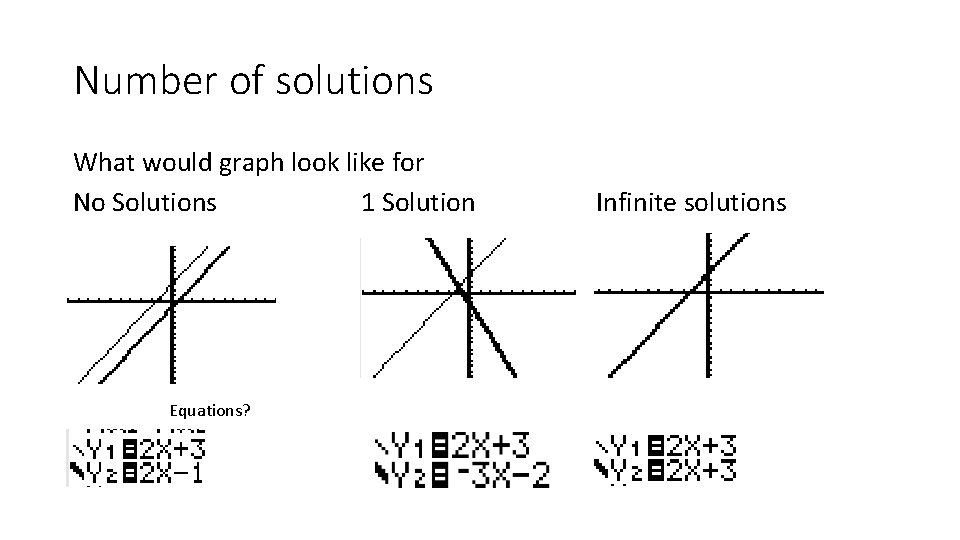
Number of solutions What would graph look like for No Solutions 1 Solution Equations? Infinite solutions

Graphically This is used a lot in word problems Determine which company is better to go with at a certain point and why, intersections tell you this. Intersection they are the same To the left one is better To the right the other is better This works great if answer is exact numbers, harder if decimals This also works good if you have graph paper and you are very accurate, it is easy to make mistakes

Example Your niece wants to have a birthday party on either Mc. Donalds or Dave and Busters. Given the information below set up a system of equations and graph them Mc. Donalds: The fixed cost to set up is $75 and $5 for each person attending. Write an equation in slope intercept form to represent this. Dave and Busters: The fixed cost to set up is $50 and $10 for each person attending. Write an equation in slope intercept form to represent this. If you write the equations first and then graph like previous example you then use the graph to answer the following questions. y = 5 x+75 y = 10 x+50 Once you have them graphed answer the following questions. 1. At what number of guest is the cost equal? How do you know? 2. What is the difference in cost for 20 people to go to Dave and Busters vs Mc. Donalds? 3. When is it better to go to Dave and Busters vs Mc. Donalds and when is it better to go to Mc. Donalds vs Dave and Busters? 4. You want to invite 24 people to the part. How much will it cost at each location? 5. You have a $250 limit on the cost of the party, how many people could you invite to each location?

Substitution 1. Solve one equation for a variable, look for a variable with a 1 in front of it or an even number 2. Substitute the expression you just solved for into the variable of the other equation 3. Solve for the remaining variable 4. Take value of variable and substitute it into the first equation 5. Check ordered pair in second equation 6. Write answer as an ordered pair Step 1 and 2 are really just saying set the two equations equal to each other and solve, this is usually easiest when both are already solved for y

Example Solve first equation for y Substitute first equation into second for x You could solve both for y and then set equations equal, you will get same answer no matter what

Number of solutions This works for substitution and elimination How do you determine how many solutions if not graphing No Solutions – when you solve you get 2 numbers that are not equal to each other 1 Solution x and y both equal in number, process works Infinite solutions is when x=x or a number equals itself This works great when numbers are nice and easy to work with. If you have a lot of decimals or fractions it does make it a little hard. It does work better than graphing the lines. You need to be able to solve more complex equations

Solutions Think back to the equations used for solving graphically If we solve them using substitution No solutions 1 solution Infinite solutions

Elimination Add the equations together to cancel out one of the variables 1. Line up equations so variables are above one another 2. Determine what to multiply the equations by so when you add them one of the variables will cancel, this means one coefficient is positive and one is negative 3. Add the equations together 4. Solve for remaining variable 5. Sub in value of variable into original 1 st equation and solve 6. Check answer in second equation 7. Write answer as an ordered pair

Example Multiply second equation by -3 so coefficient of x terms are opposites Then we add them together the x terms cancel leaving only the y term to solve for Sub in y value and solve for x Check ordered pair in second equation and it should be true Write as an ordered pair

Solving Inequalities Solve like a normal equation Move everything away from the variable Only difference is when you multiply or divide by a negative the sign changes directions This works great for all types, just like substitution It is a little harder with fractions

Review for 1 Variable inequalities Graphing and Writing Equations Depending on the type of inequality depends on if the circle is open or closed Open if only greater than or less than Closed if greater than or equal to, less than or equal to Put the correct circle on top of the number you are comparing to If variable is on the left the inequality points in the direction you should draw the arrow Less than is left Greater than is right

Continued Writing the equation Always put variable on the left Number it is at on the right Inequality is the same direction as the arrow If arrow is left then less than If arrow is right then greater than If solid put an equals sign under symbol If open do not

Linear Inequalities in the form of y=mx+b, but with an inequality Very Similar to linear equations Solve inequality for y Graph line like normal If just greater than or less than you use a dashed lines, similar to an open circle If it is also equal to you use a solid line Then you have to shade the graph because there are multiple solutions To do this test a point not on the line If the equation come back true shade on that side of the line If it comes back false shade on the other side of the line

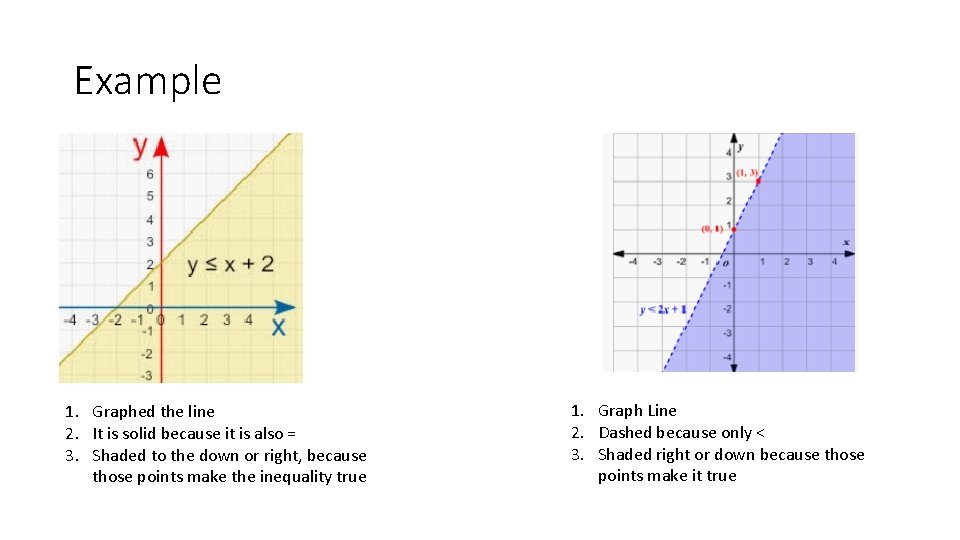
Example 1. Graphed the line 2. It is solid because it is also = 3. Shaded to the down or right, because those points make the inequality true 1. Graph Line 2. Dashed because only < 3. Shaded right or down because those points make it true

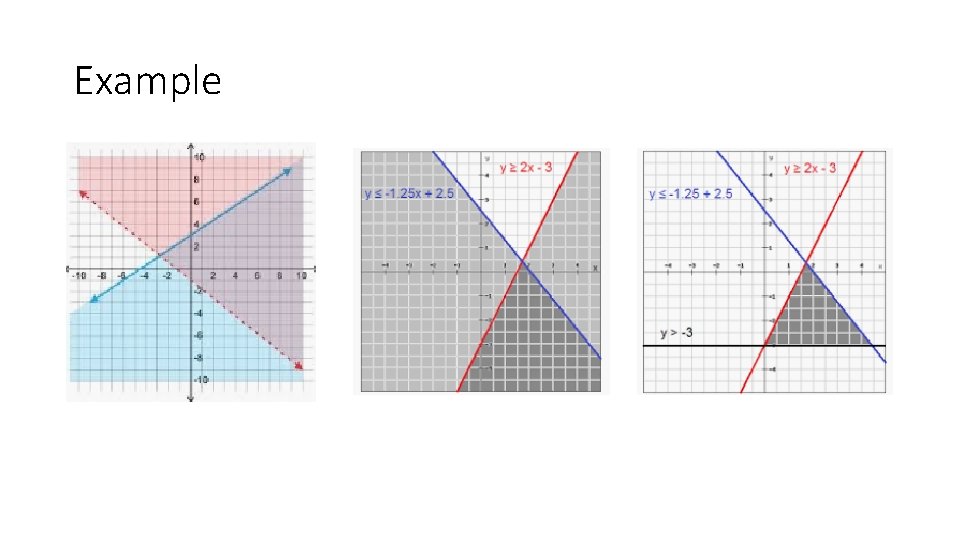
Systems of Linear Inequalities Similar to other systems we did You have multiple lines to graph and shade You are looking for the overlapping region of feasible region of all the lines Don’t shade heavy to begin with just draw arrows to indicate direction and when all lines are drawn and arrows indicated shade the main overlapping region

Example

Writing Linear Inequalities Again similar to writing equations of lines from a graph, think of how you write equation of line but instead of = you need an inequality 1. Determine slope 2. Find y –intercept 3. Is line solid or dashed indicates inequality 4. Pic a point in the shaded region, sub into equation to help determine which inequality to use

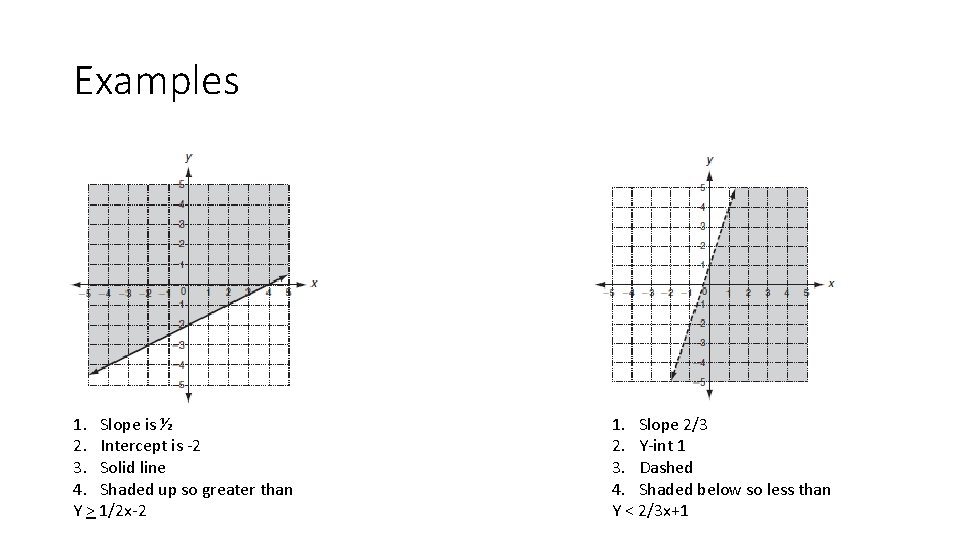
Examples 1. Slope is ½ 2. Intercept is -2 3. Solid line 4. Shaded up so greater than Y > 1/2 x-2 1. Slope 2/3 2. Y-int 1 3. Dashed 4. Shaded below so less than Y < 2/3 x+1

Word Problems Be able to write the inequality from a word problem and then graph it to get solutions Apply rules already learned and use the graph to help answer questions

Linear Inequalities 1. Solve for y 2. Graph line 1. Solid if equal to 2. Dashed if not equal 3. Shade one side of the line 1. Test a point on one side of the line, if it is true shade on that side, if it is false shade on opposite side 2. Similar to graphing on a number line, but look at y axis, greater goes up, less goes down 4. Look for overlapping area when graphing multi inequalities