Honors Physics Vectors l Chapter Problems All problems

Honors Physics Vectors l Chapter Problems All problems prior to Mixed review l Vector addition graphically A vector can be represented by an arrow tipped line segment Honors Physics , Pg 1

Vectors. . . l There are two common ways of indicating that something is a vector quantity: çBoldface notation: A A= ç“Arrow” notation: A “Hat” Notation Honors Physics , Pg 2

Vectors. . . l The components of r are it’s (x, y, z) coordinates. ç r = (rx , ry , rz ) = (x, y, z) l Consider this in 2 -D (since it’s easier to draw): çrx = r cos f where r = |r | çry = r sin f (x, y) y f = arctan( y / x ) r f x NOTE: The book uses q instead of f. No big deal. Honors Physics , Pg 3

Vectors. . . l The magnitude (length) of r is found using Pythagoras’ theorem: r y x l The length of a vector clearly does not depend on it’s direction. Honors Physics , Pg 4

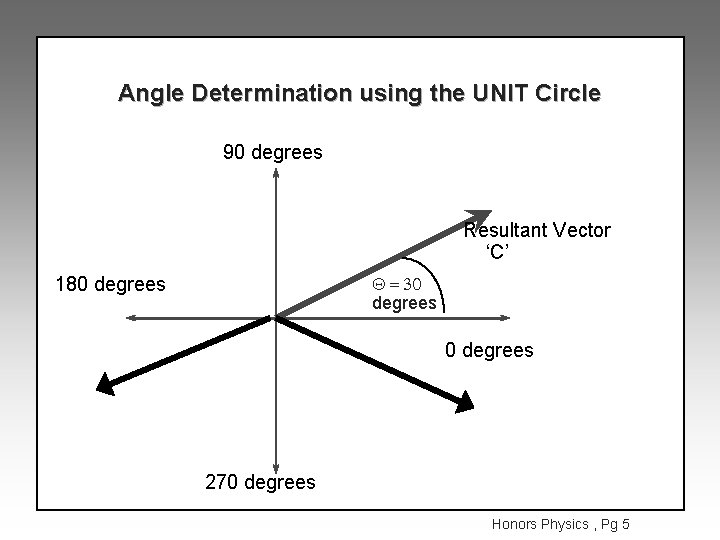
Angle Determination using the UNIT Circle 90 degrees Resultant Vector ‘C’ Q = 30 degrees 180 degrees 270 degrees Honors Physics , Pg 5

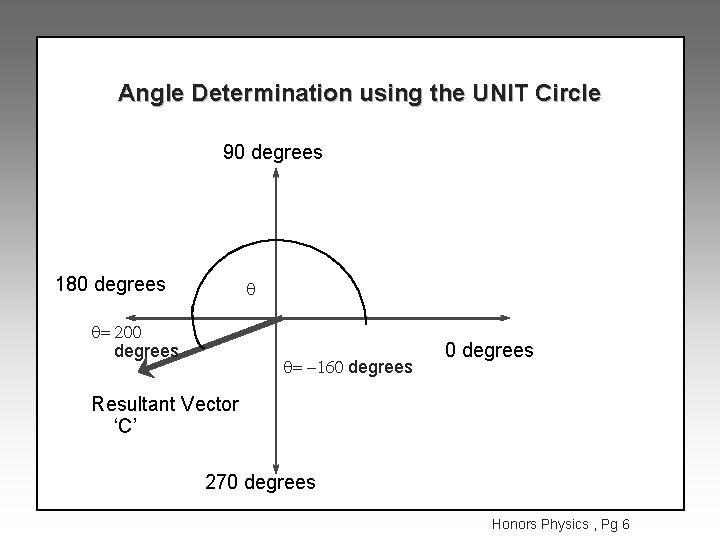
Angle Determination using the UNIT Circle 90 degrees 180 degrees q q= 200 degrees q= -160 degrees Resultant Vector ‘C’ 270 degrees Honors Physics , Pg 6

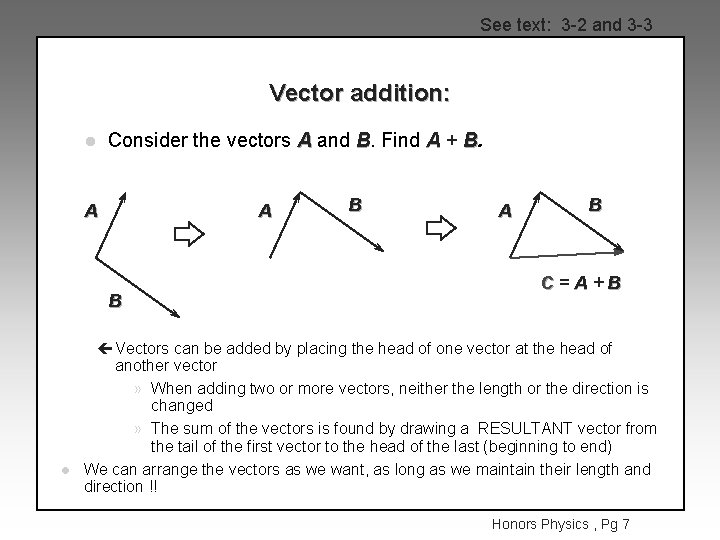
See text: 3 -2 and 3 -3 Vector addition: l Consider the vectors A and B. Find A + B. A A B l B A B C=A+B çVectors can be added by placing the head of one vector at the head of another vector » When adding two or more vectors, neither the length or the direction is changed » The sum of the vectors is found by drawing a RESULTANT vector from the tail of the first vector to the head of the last (beginning to end) We can arrange the vectors as we want, as long as we maintain their length and direction !! Honors Physics , Pg 7

Addition of several vectors Two students are pulling concurrently (same place, same time)5 N , 0 degrees and 7 N, 270 degrees on a 20 kg oscilloscope (assume a frictionless surface) a) determine the direction of motion b) determine the net force and acceleration of the scope l 5 N 0 degrees 7 N 270 degrees Honors Physics , Pg 8

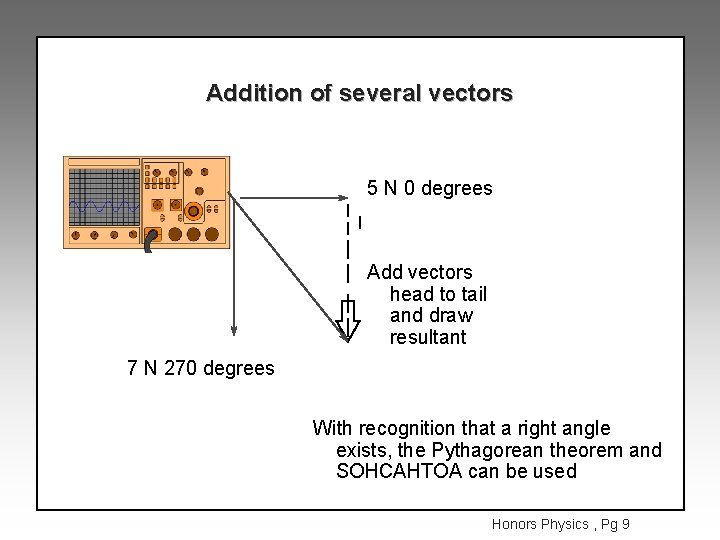
Addition of several vectors 5 N 0 degrees Add vectors head to tail and draw resultant 7 N 270 degrees With recognition that a right angle exists, the Pythagorean theorem and SOHCAHTOA can be used Honors Physics , Pg 9

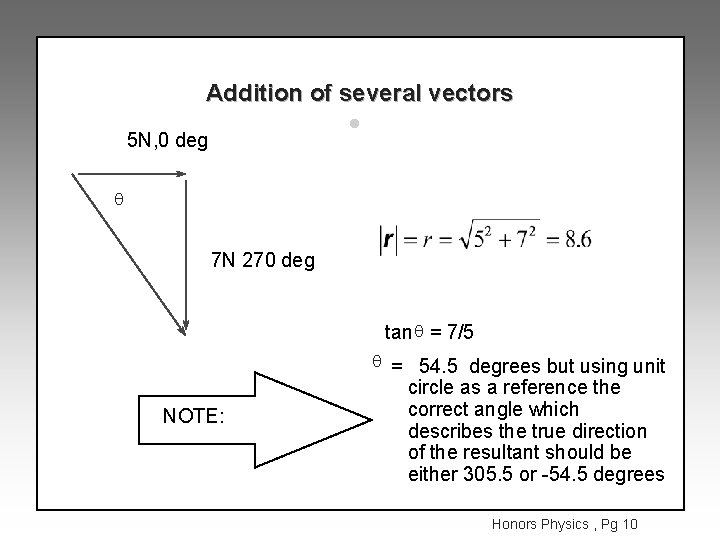
Addition of several vectors l 5 N, 0 deg q 7 N 270 deg tan q = 7/5 q = 54. 5 degrees but using unit NOTE: circle as a reference the correct angle which describes the true direction of the resultant should be either 305. 5 or -54. 5 degrees Honors Physics , Pg 10

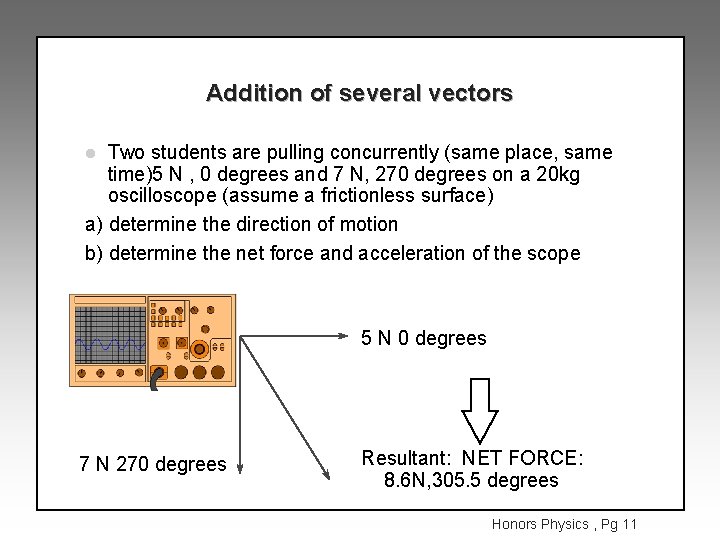
Addition of several vectors Two students are pulling concurrently (same place, same time)5 N , 0 degrees and 7 N, 270 degrees on a 20 kg oscilloscope (assume a frictionless surface) a) determine the direction of motion b) determine the net force and acceleration of the scope l 5 N 0 degrees 7 N 270 degrees Resultant: NET FORCE: 8. 6 N, 305. 5 degrees Honors Physics , Pg 11

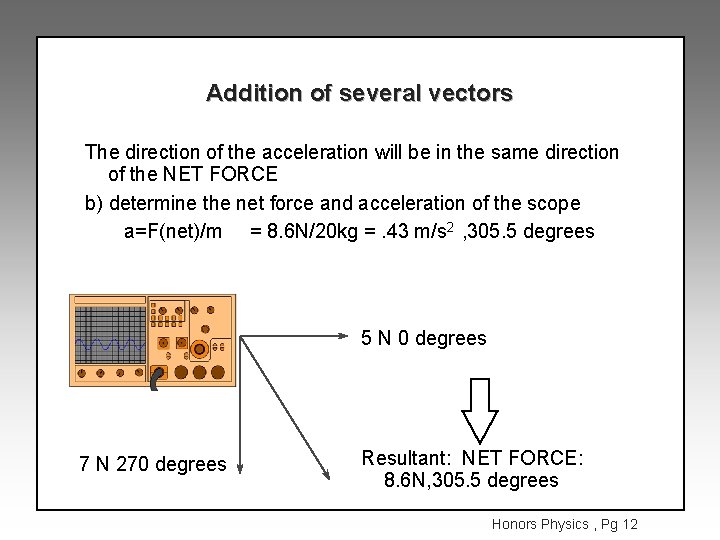
Addition of several vectors The direction of the acceleration will be in the same direction of the NET FORCE b) determine the net force and acceleration of the scope a=F(net)/m = 8. 6 N/20 kg =. 43 m/s 2 , 305. 5 degrees 5 N 0 degrees 7 N 270 degrees Resultant: NET FORCE: 8. 6 N, 305. 5 degrees Honors Physics , Pg 12

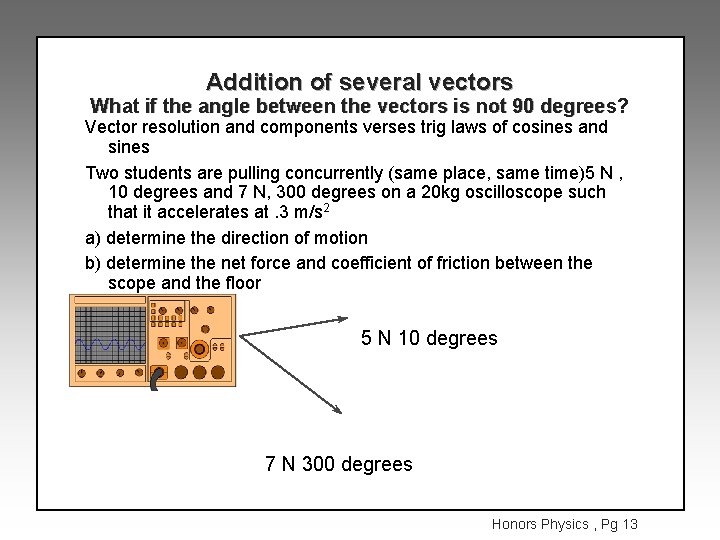
Addition of several vectors What if the angle between the vectors is not 90 degrees? Vector resolution and components verses trig laws of cosines and sines Two students are pulling concurrently (same place, same time)5 N , 10 degrees and 7 N, 300 degrees on a 20 kg oscilloscope such that it accelerates at. 3 m/s 2 a) determine the direction of motion b) determine the net force and coefficient of friction between the scope and the floor 5 N 10 degrees 7 N 300 degrees Honors Physics , Pg 13

Vector addition using components: l Consider C = A + B. l ç (a) C = (Ax i + Ay j ) + (Bx i + By j ) = (Ax + Bx )i + (Ay + By )j ç (b) C = (Cx i + Cy j ) Comparing components of (a) and (b): ç Cx = A x + B x ç Cy = A y + B y C B By A Ay Bx Ax Honors Physics , Pg 14

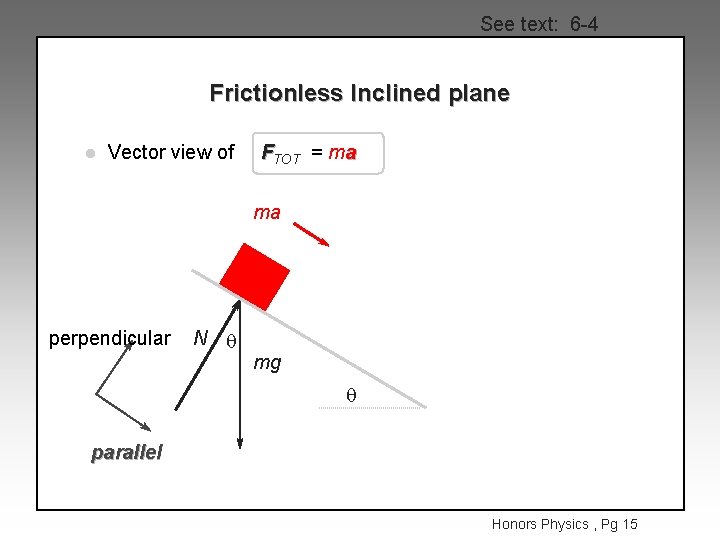
See text: 6 -4 Frictionless Inclined plane l Vector view of FTOT = ma ma perpendicular N q mg q parallel Honors Physics , Pg 15

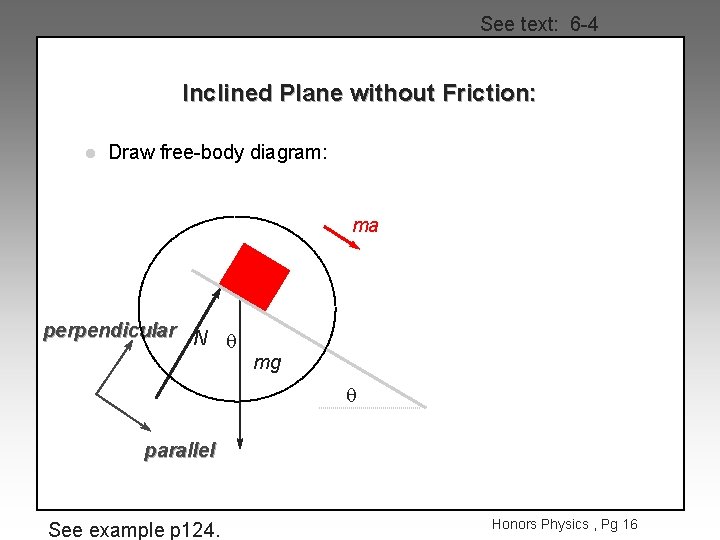
See text: 6 -4 Inclined Plane without Friction: l Draw free-body diagram: ma perpendicular N q mg q parallel See example p 124. Honors Physics , Pg 16

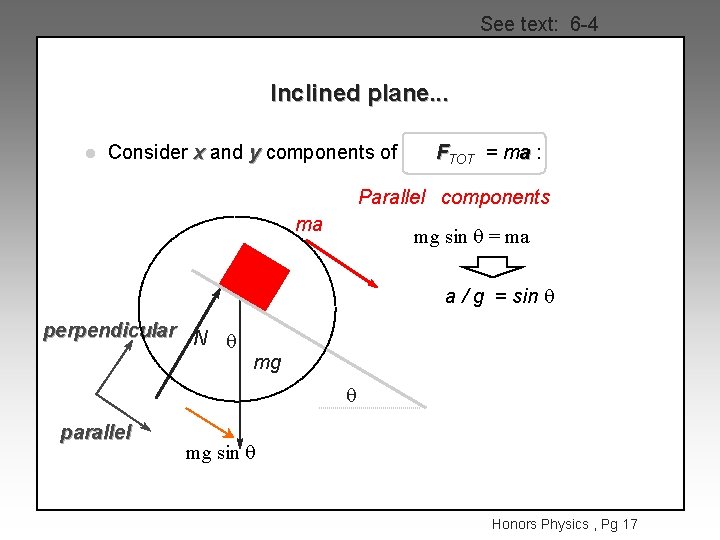
See text: 6 -4 Inclined plane. . . l Consider x and y components of FTOT = ma : Parallel components ma mg sin q = ma a / g = sin q perpendicular N q mg q parallel mg sin q Honors Physics , Pg 17

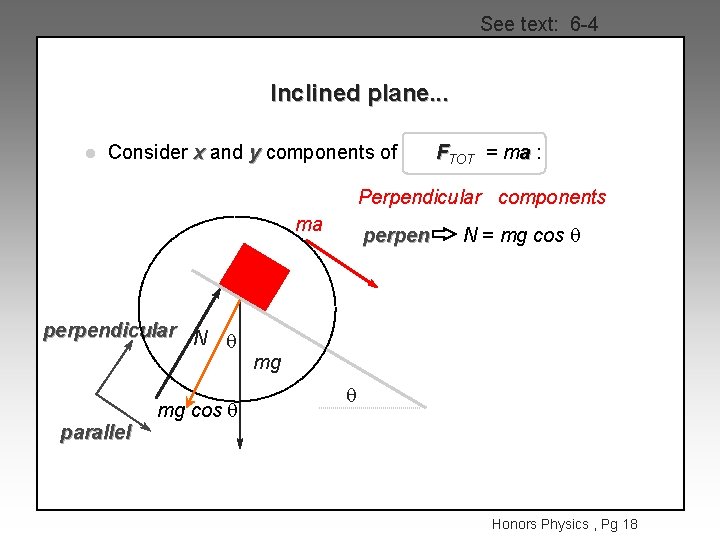
See text: 6 -4 Inclined plane. . . l Consider x and y components of FTOT = ma : Perpendicular components ma perpendicular N q parallel mg cos q perpen N = mg cos q mg q Honors Physics , Pg 18

See text: 6 -4 Static Friction: l So far we have considered friction acting when something moves. çWe also know that it acts in un-moving “static” systems: q In these cases, the force provided by friction will depend on the configuration of the system (i. e. angle q of the plane). Honors Physics , Pg 19

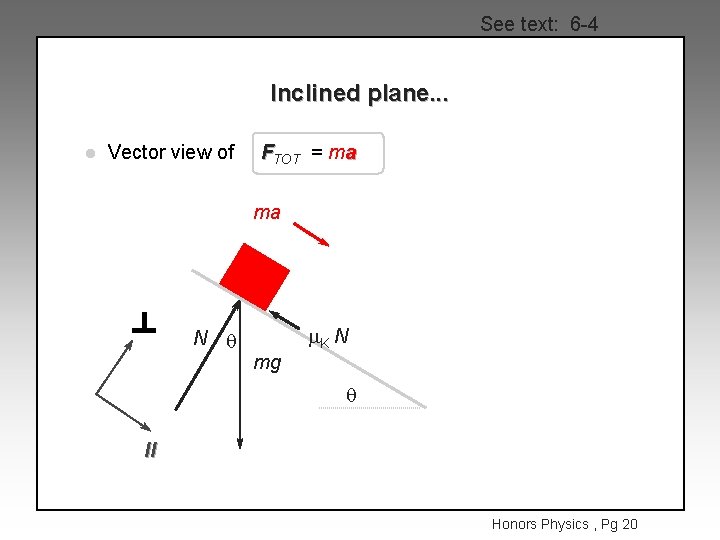
See text: 6 -4 Inclined plane. . . l Vector view of FTOT = ma ma N q mg m. K N q ll Honors Physics , Pg 20

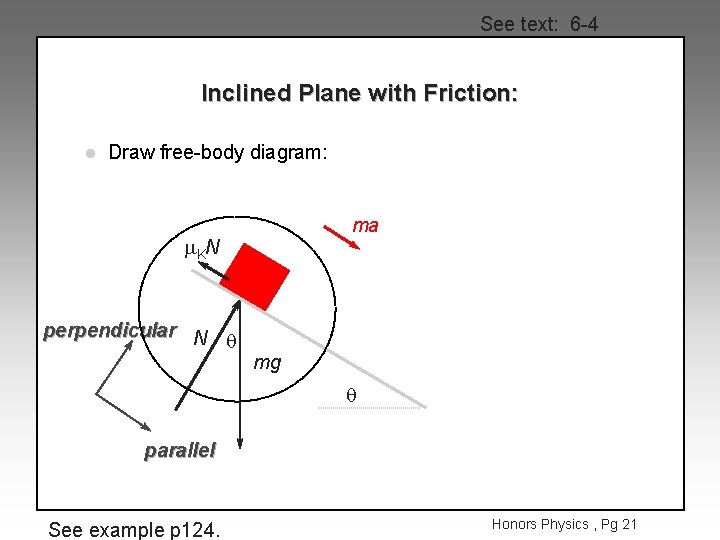
See text: 6 -4 Inclined Plane with Friction: l Draw free-body diagram: ma m. KN perpendicular N q mg q parallel See example p 124. Honors Physics , Pg 21

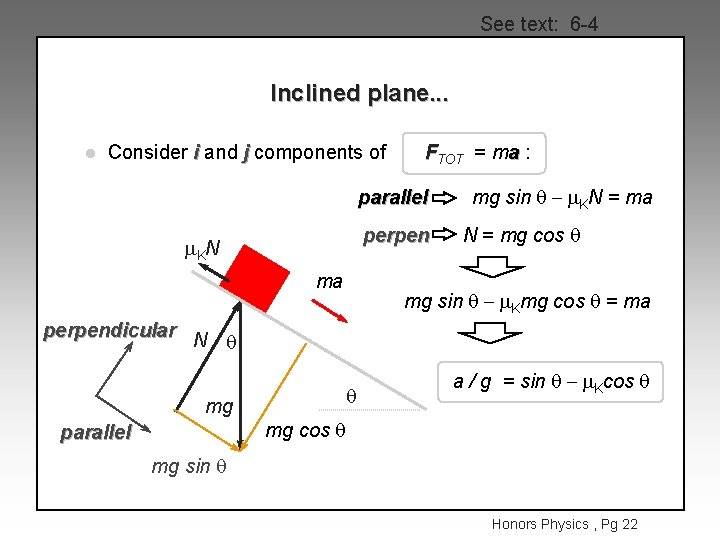
See text: 6 -4 Inclined plane. . . l Consider i and j components of FTOT = ma : parallel perpen m. KN ma mg sin q - m. KN = ma N = mg cos q mg sin q - m. Kmg cos q = ma perpendicular N q mg parallel q a / g = sin q - m. Kcos q mg sin q Honors Physics , Pg 22

See text: 6 -4 Static Friction. . . l The force provided by friction, f. F , depends on q as long as the block is “static”. f. F ma = 0 (block is not moving) mg sin q - ff = 0 N q (Newtons 2 nd law along x-axis) mg q See example p 126: Static Friction Honors Physics , Pg 23

See text: 6 -4 Static Friction. . . l Definition: The maximum possible force that the friction between two objects can provide is f. MAX = ms. N, where ms is the “static coefficient of friction”. çWe can find ms by increasing the ramp angle until the block slides: In this case: m. SN ma = mg sin q. M - m. Smg cos q. M = 0 N q. M mg q See example p 126 Static Friction m. S = tan q. M Honors Physics , Pg 24

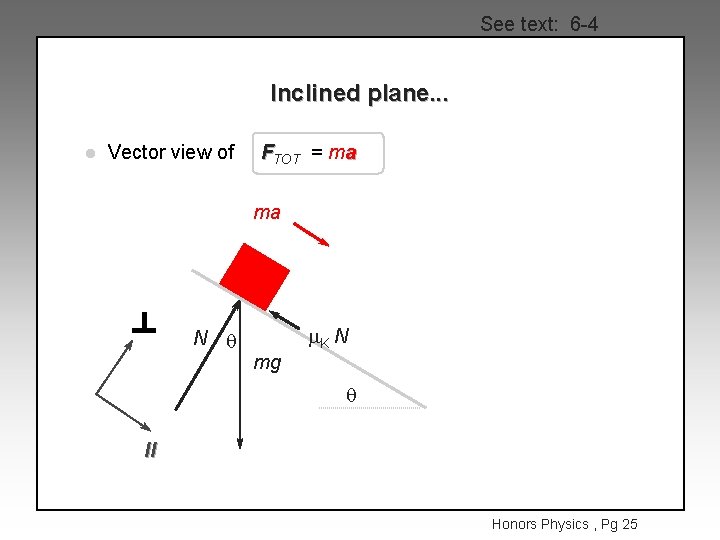
See text: 6 -4 Inclined plane. . . l Vector view of FTOT = ma ma N q mg m. K N q ll Honors Physics , Pg 25

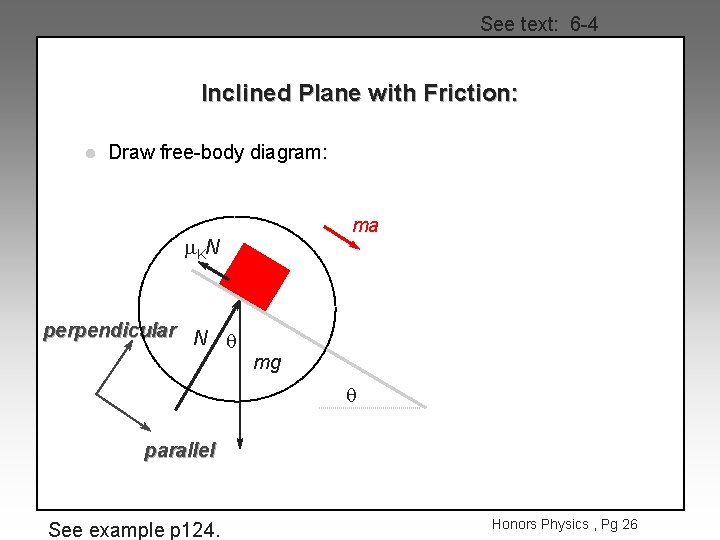
See text: 6 -4 Inclined Plane with Friction: l Draw free-body diagram: ma m. KN perpendicular N q mg q parallel See example p 124. Honors Physics , Pg 26

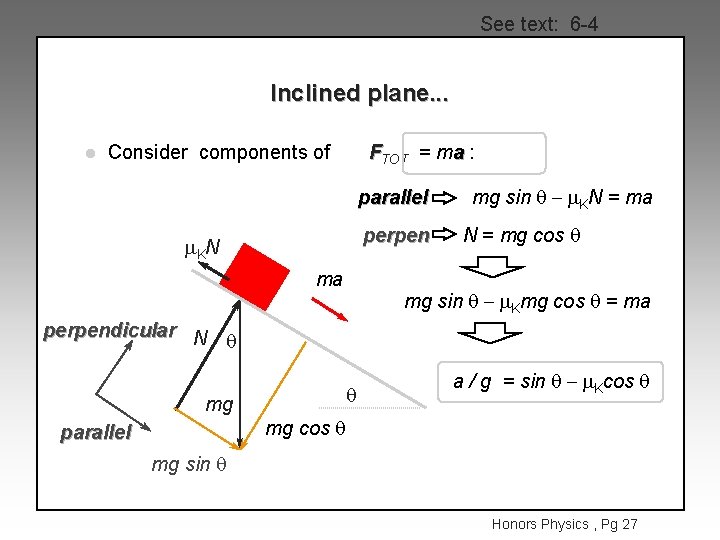
See text: 6 -4 Inclined plane. . . l Consider components of FTOT = ma : parallel perpen m. KN ma mg sin q - m. KN = ma N = mg cos q mg sin q - m. Kmg cos q = ma perpendicular N q mg parallel q a / g = sin q - m. Kcos q mg sin q Honors Physics , Pg 27