Honors Geometry Areas What is area When we

Honors Geometry Areas

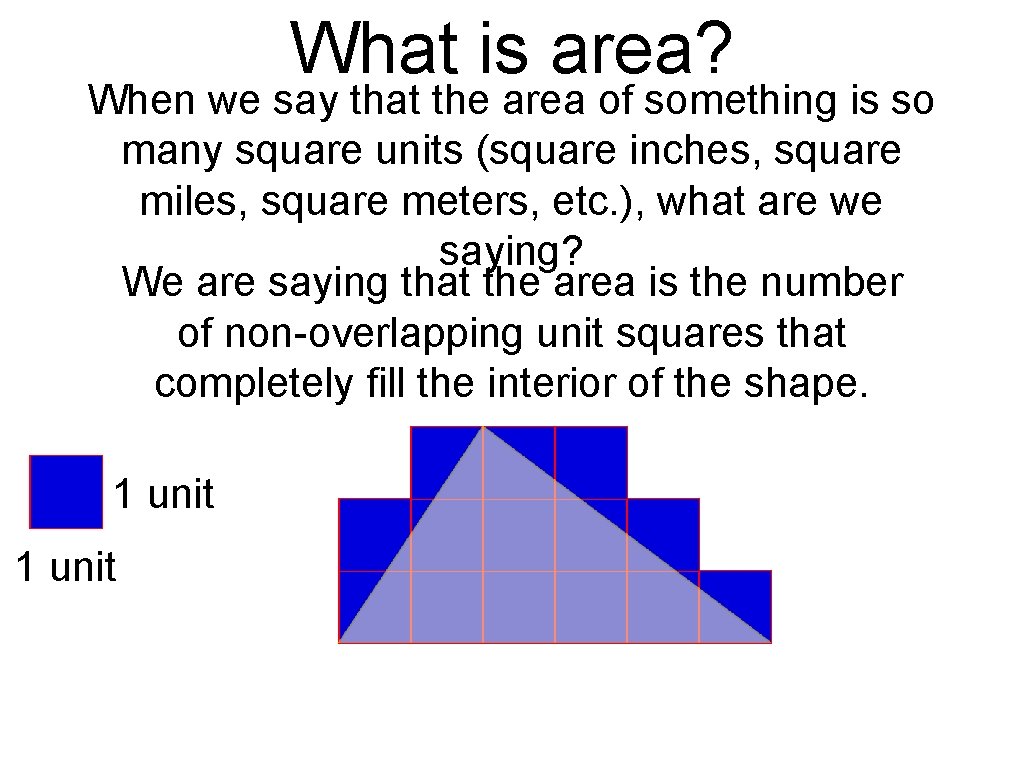
What is area? When we say that the area of something is so many square units (square inches, square miles, square meters, etc. ), what are we saying? We are saying that the area is the number of non-overlapping unit squares that completely fill the interior of the shape. 1 unit

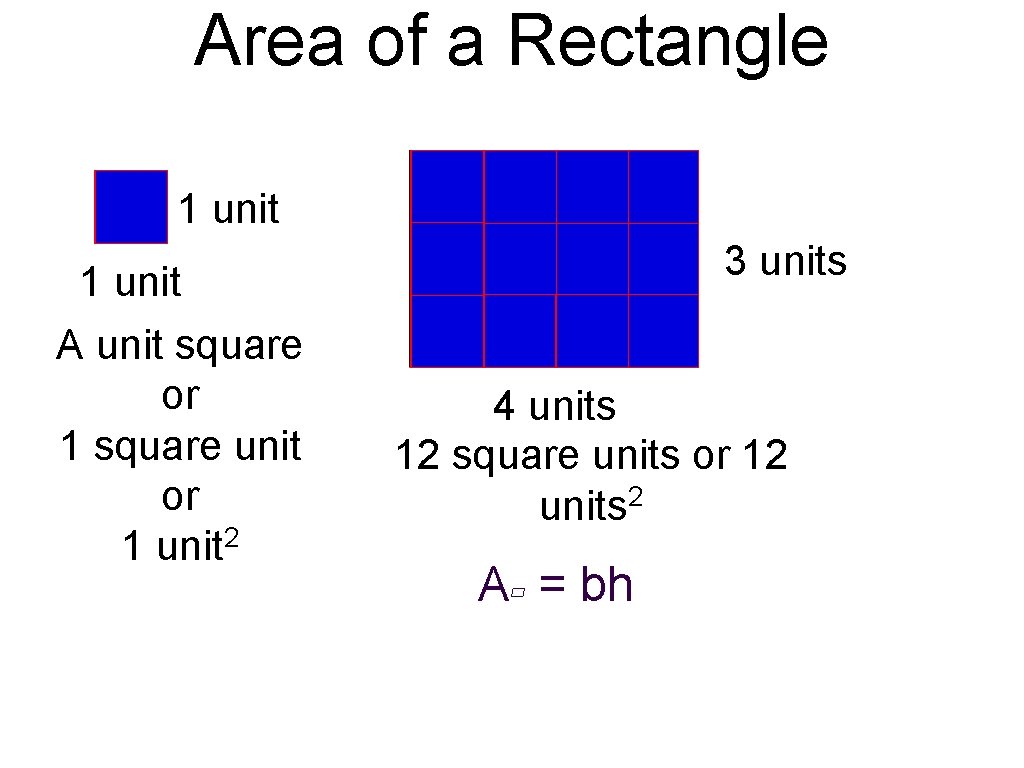
Area of a Rectangle 1 unit 3 units 1 unit A unit square or 1 square unit or 2 1 unit 4 units 12 square units or 12 units 2 A▱ = bh

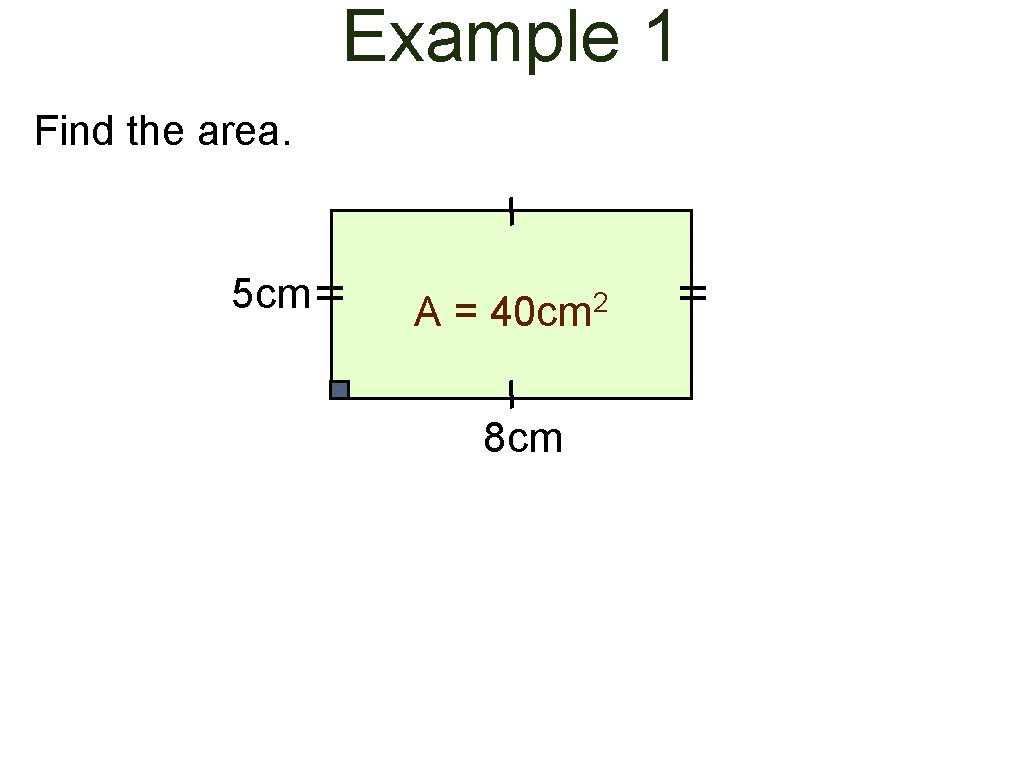
Example 1 Find the area. 5 cm A = 40 cm 2 8 cm

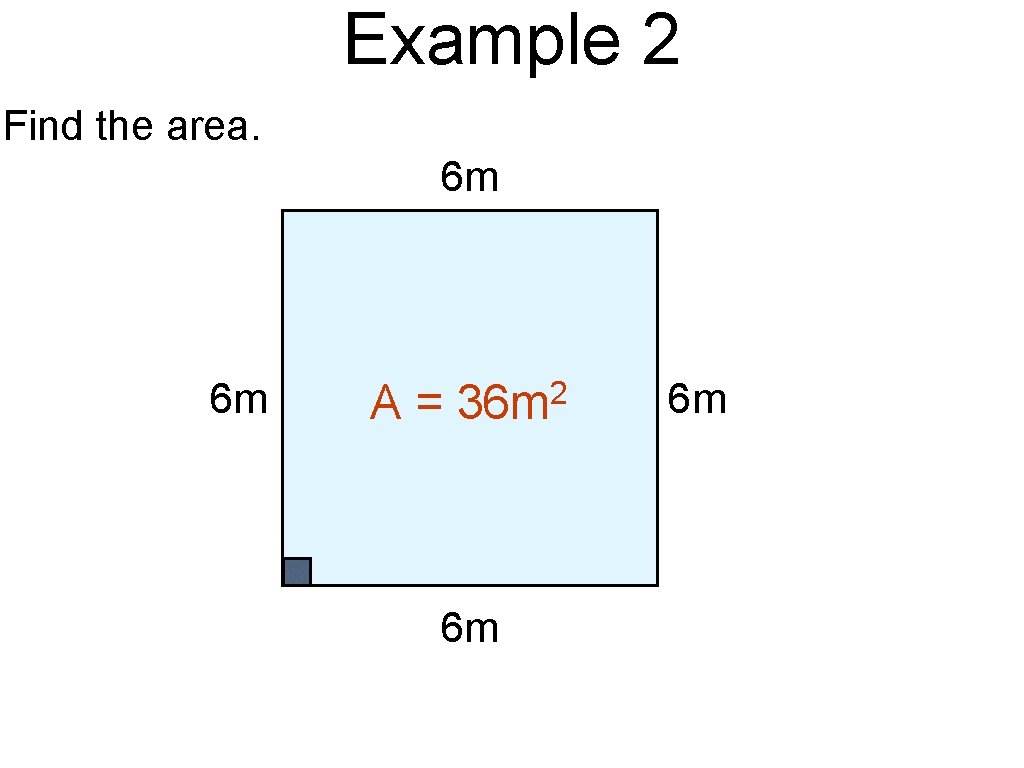
Example 2 Find the area. 6 m 6 m A= 2 36 m 6 m 6 m

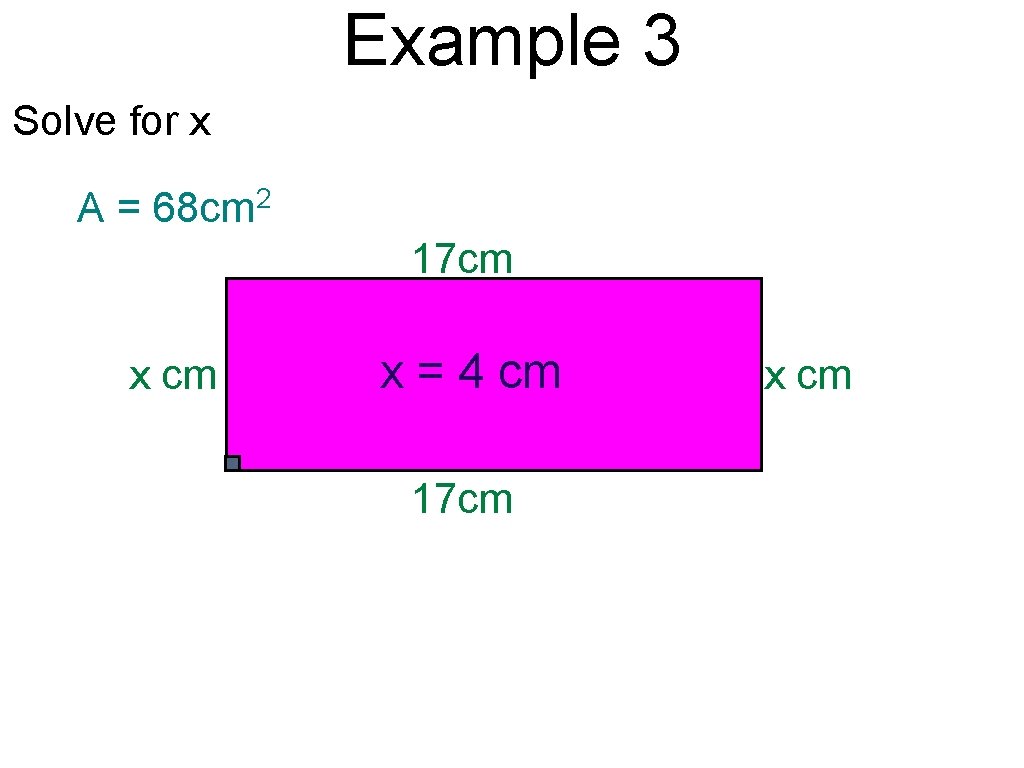
Example 3 Solve for x A = 68 cm 2 17 cm x = 4 cm 17 cm x cm

Area of a Parallelogram A▱ = bh Where height (h) is an altitude (a perpendicular segment from a vertex to a non-adjacent side). Since rectangles, rhombi and squares are also parallelograms, this formula applies to them as well.

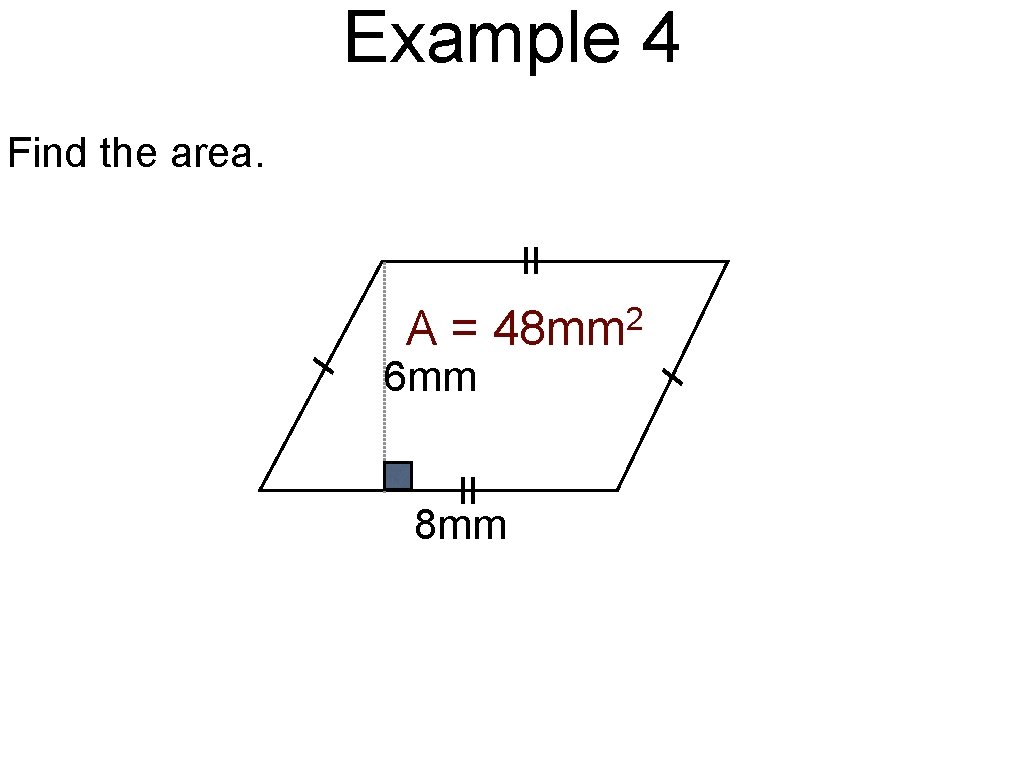
Example 4 Find the area. A= 6 mm 2 48 mm

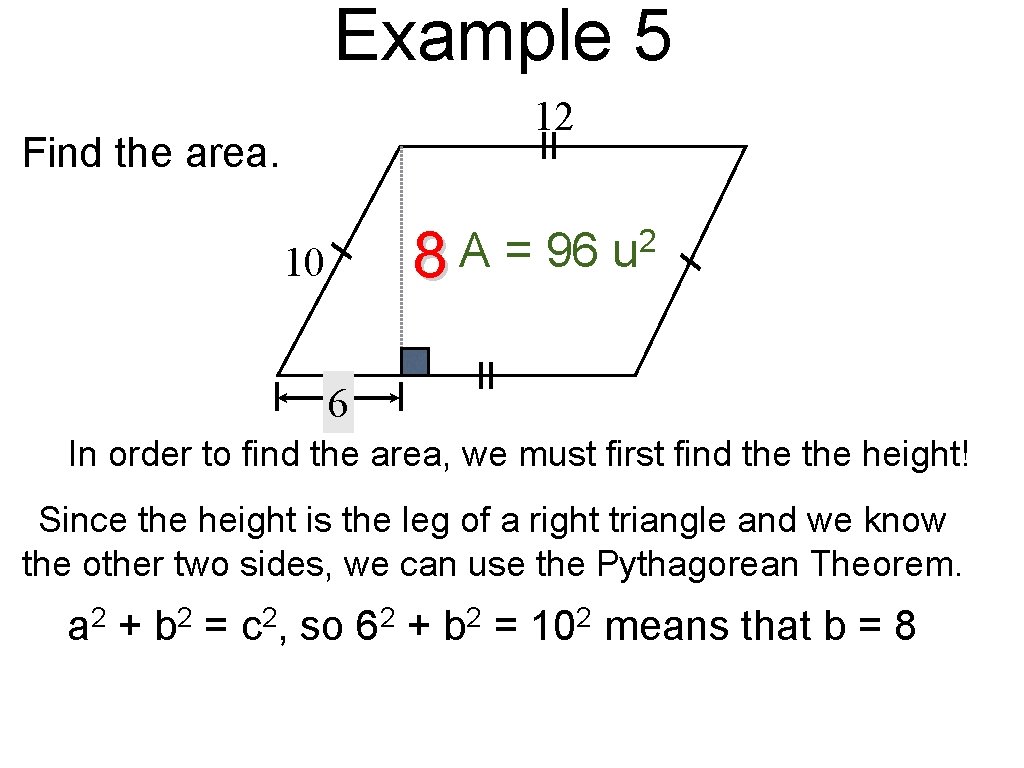
Example 5 12 Find the area. 8 A = 96 10 2 u 6 In order to find the area, we must first find the height! Since the height is the leg of a right triangle and we know the other two sides, we can use the Pythagorean Theorem. 2 a + 2 b = 2 c, so 2 6 + 2 b = 2 10 means that b = 8

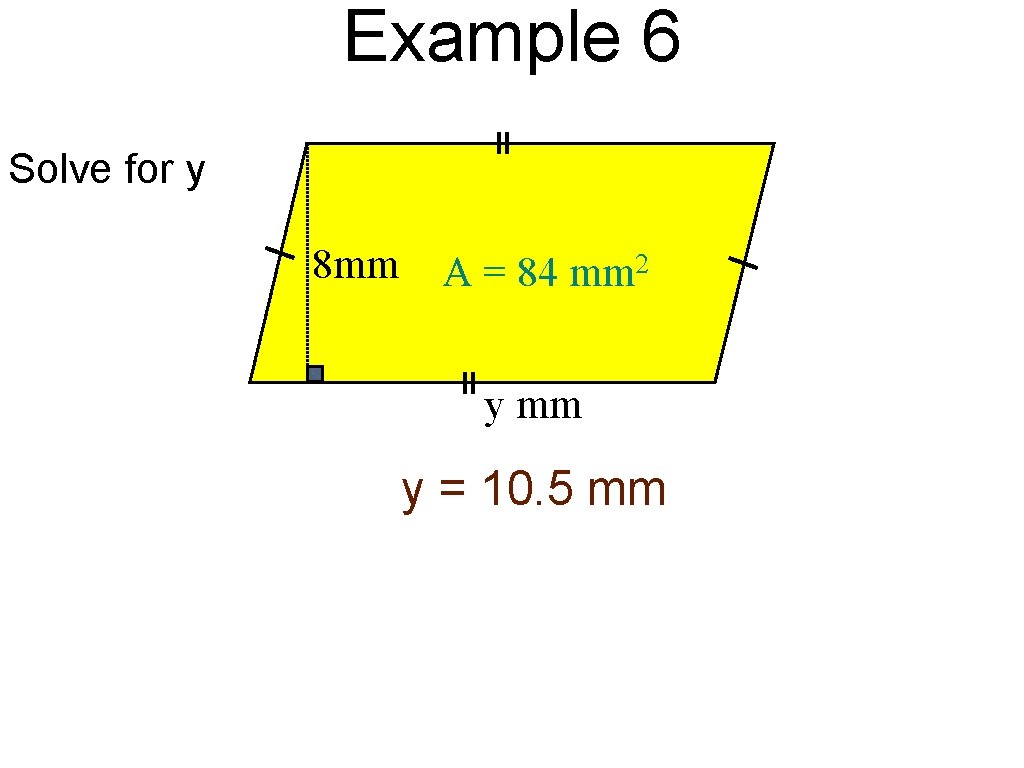
Example 6 Solve for y 8 mm A = 84 mm 2 y mm y = 10. 5 mm

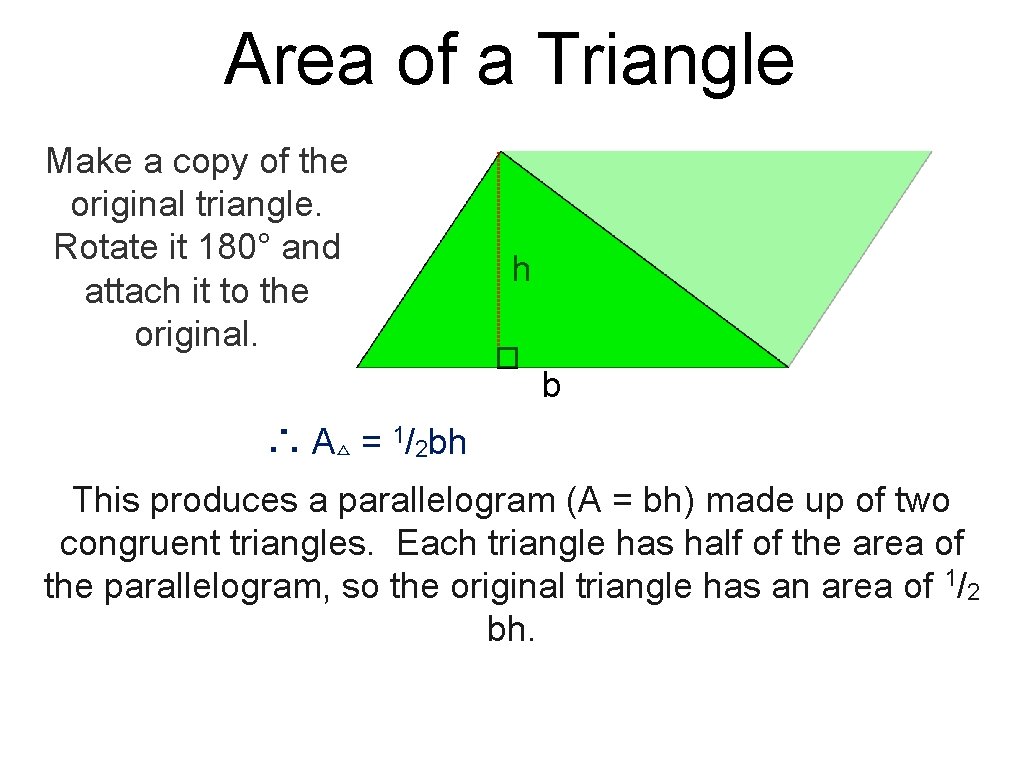
Area of a Triangle Make a copy of the original triangle. Rotate it 180° and attach it to the original. h b ∴ A△ = 1/2 bh This produces a parallelogram (A = bh) made up of two congruent triangles. Each triangle has half of the area of the parallelogram, so the original triangle has an area of 1/2 bh.

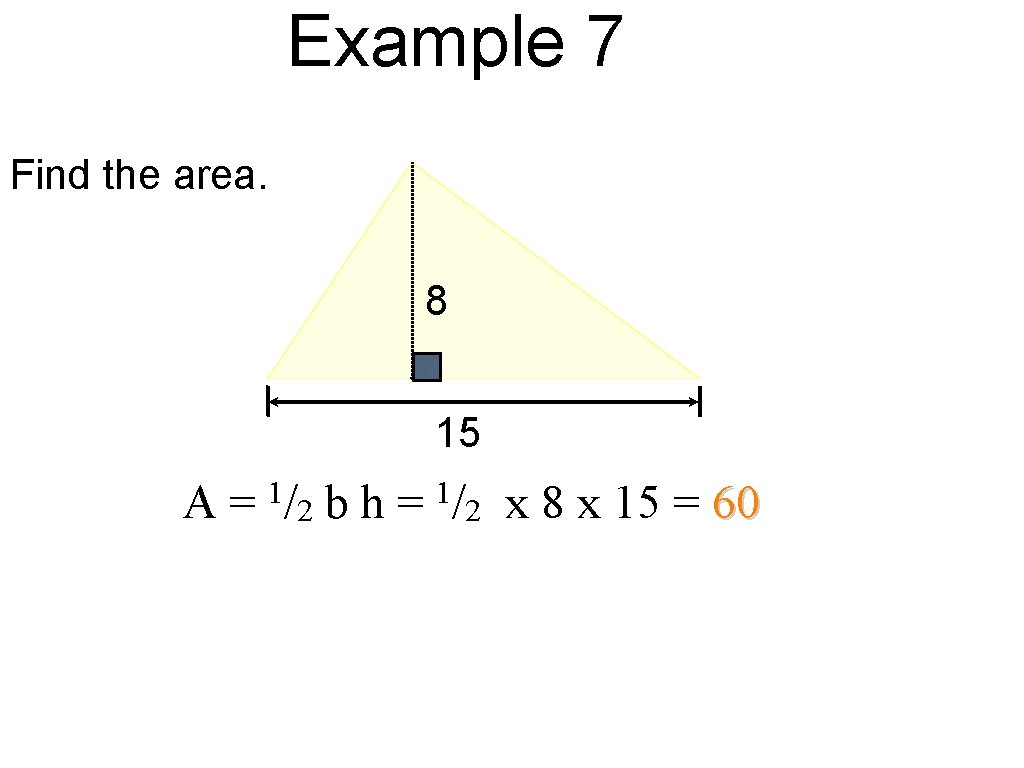
Example 7 Find the area. 8 15 A= 1/ 2 bh= 1/ 2 x 8 x 15 = 60

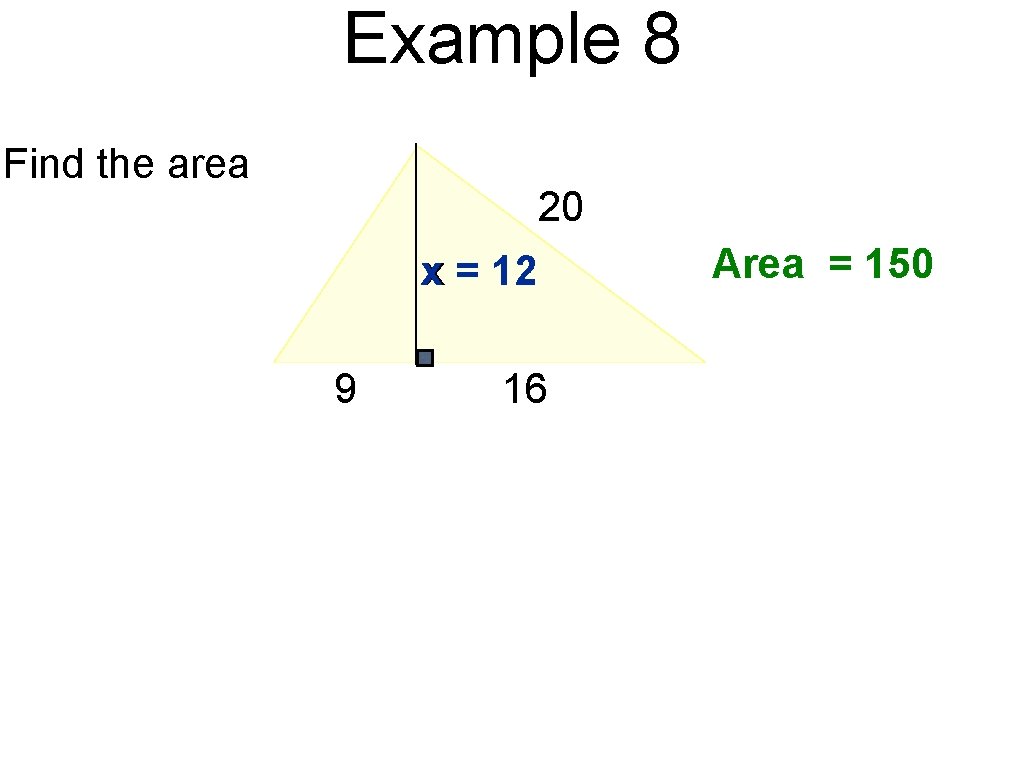
Example 8 Find the area 20 x = 12 9 16 Area = 150

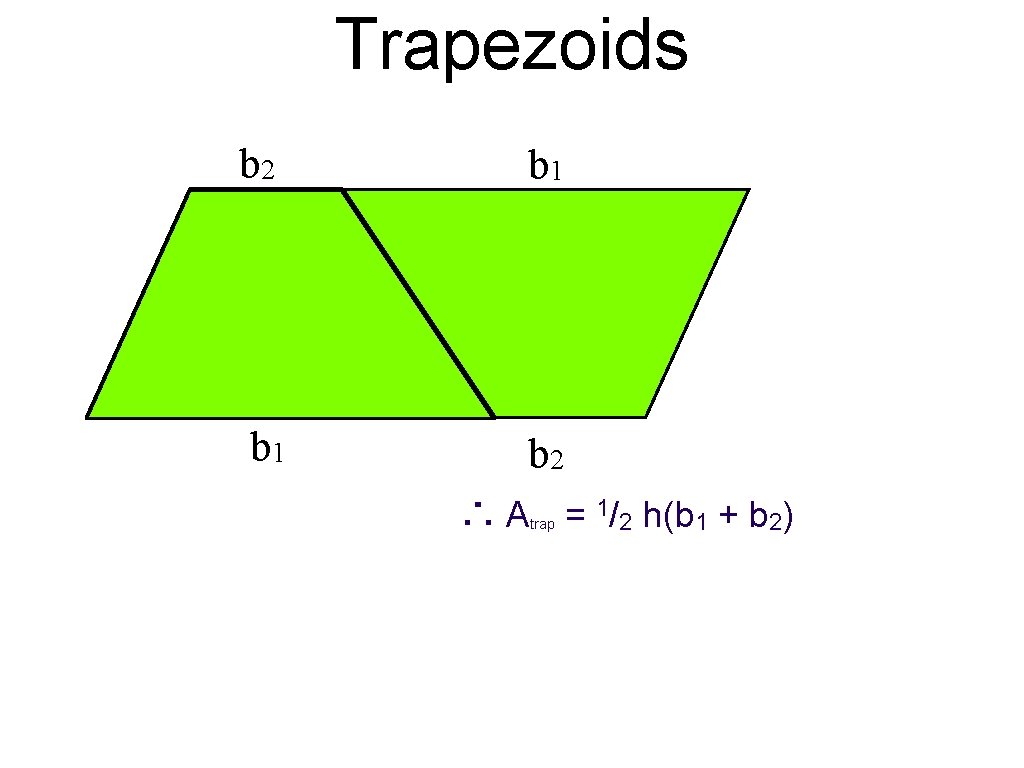
Trapezoids b 2 b 1 b 2 h ∴ Atrap = 1/2 h(b 1 + b 2)

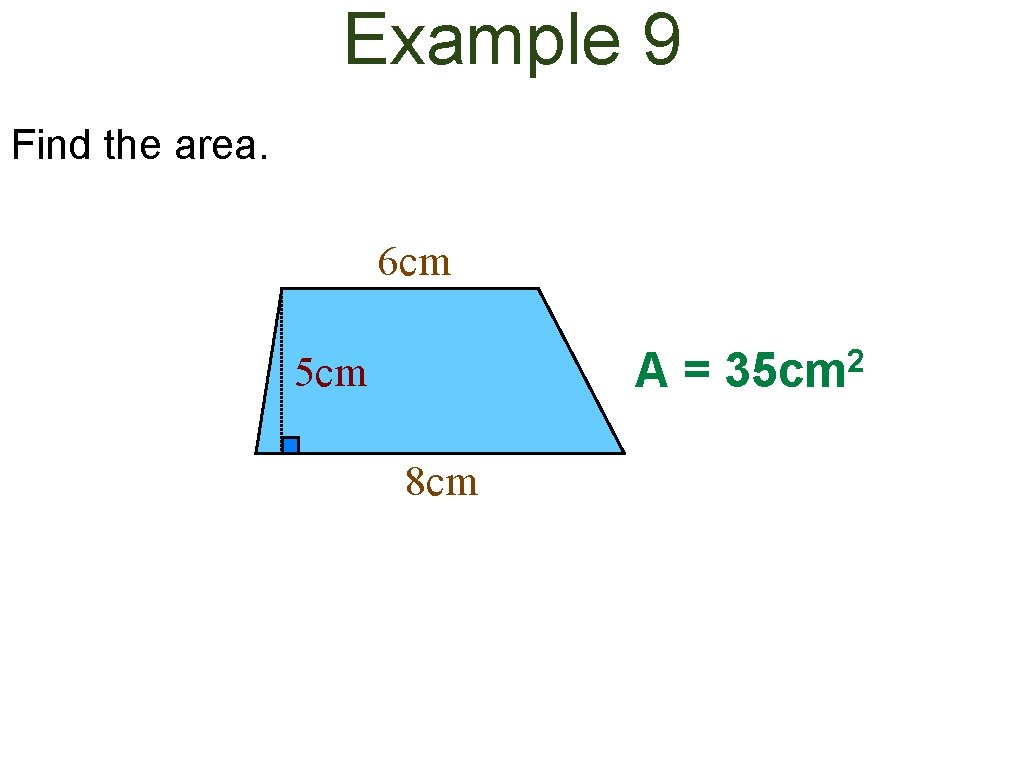
Example 9 Find the area. 6 cm A= 5 cm 8 cm 2 35 cm

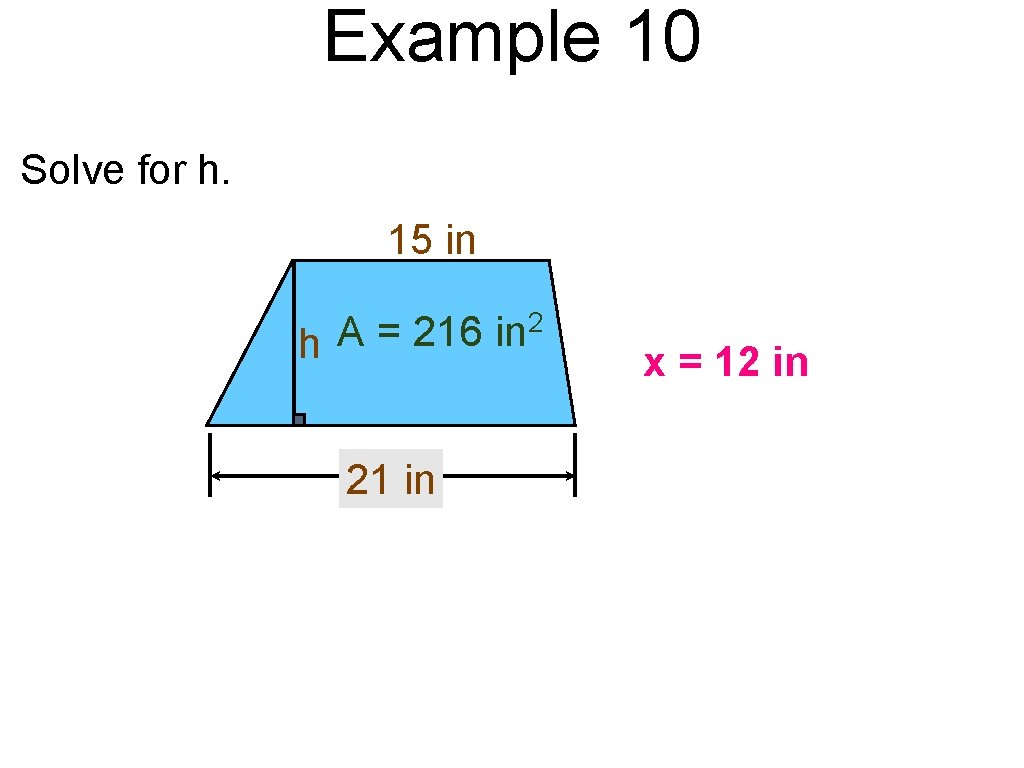
Example 10 Solve for h. 15 in 2 A = 216 in h 21 in x = 12 in

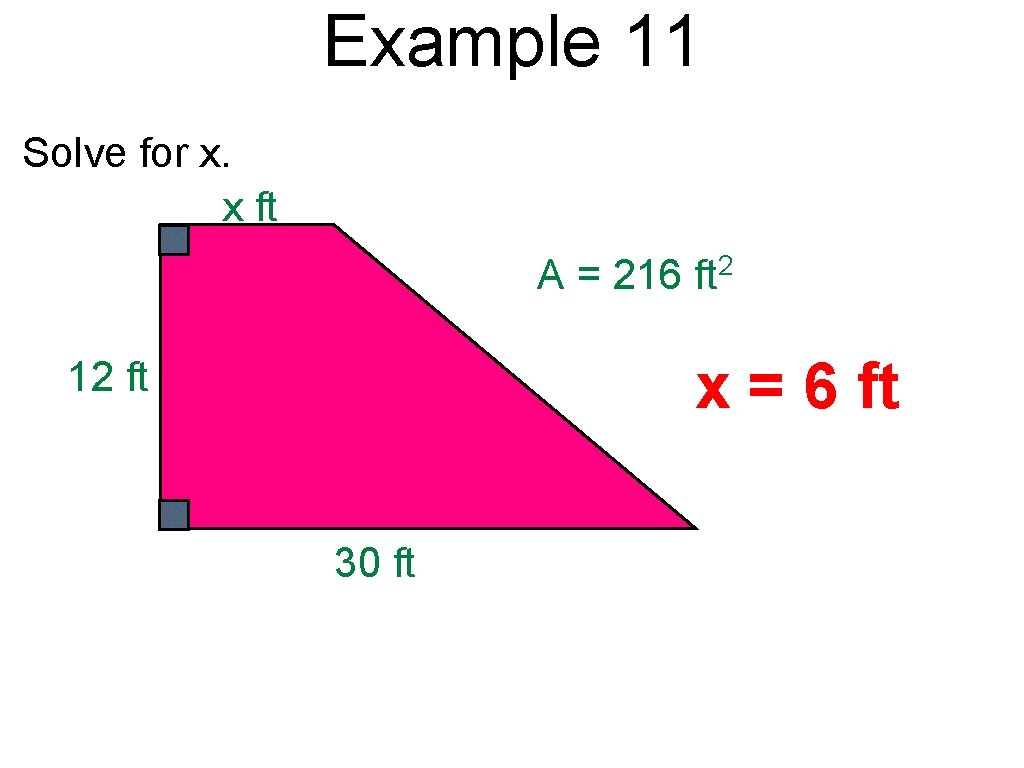
Example 11 Solve for x. x ft A = 216 2 ft x = 6 ft 12 ft 30 ft

A Special Formula A formula that applies to a few special circumstances can best be illustrated using a kite. d 2 = a + b d 1 = 2 c c c a b c The area of the rectangle shown is c(a + b) which is equal to the area of the kite. But c = 1/2 d 1 and a + b = d 2, so the area of the kite is equal to 1/2 d 1 • d 2 !!! This formula also applies to ALL other quadrilaterals with perpendicular diagonals such as rhombi and squares !!!

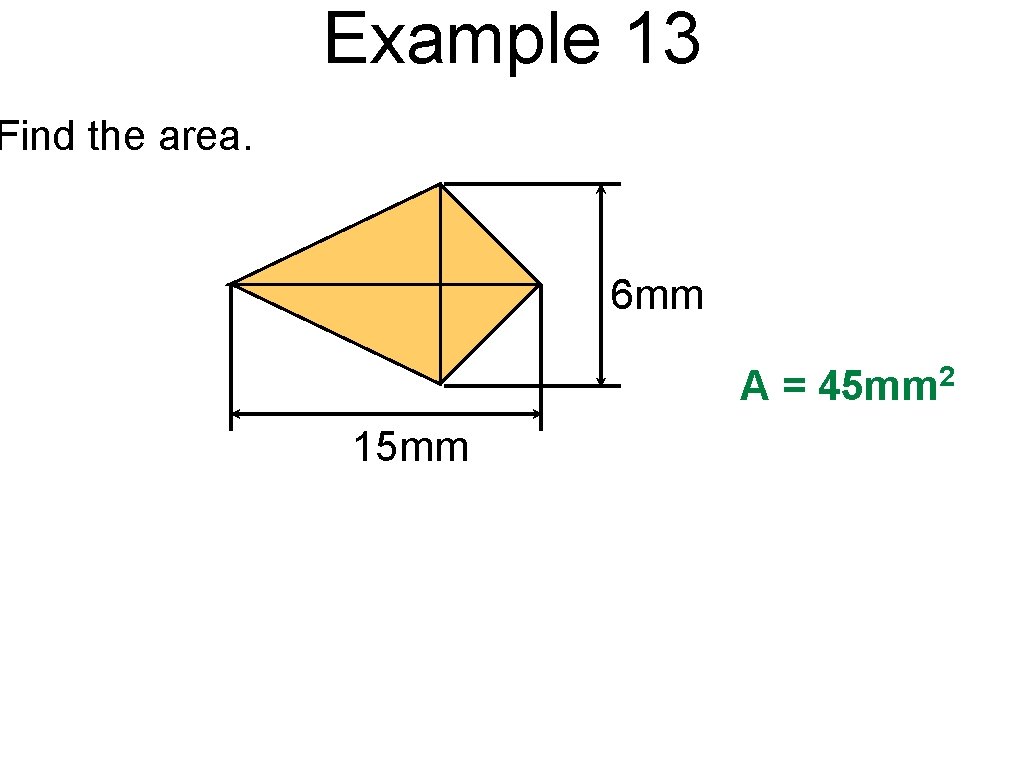
Example 13 Find the area. 6 mm A = 45 mm 2 15 mm

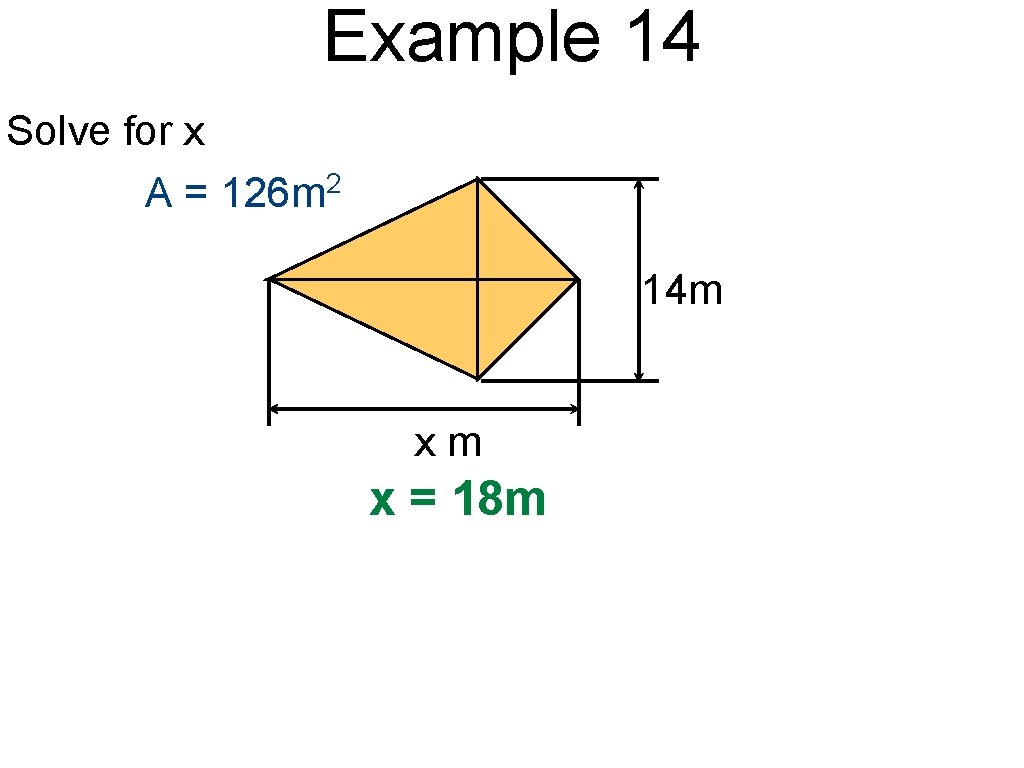
Example 14 Solve for x A = 126 m 2 14 m xm x = 18 m

Assignment 11. 1 Practice C - odds 11. 2 Practice C - odds

Honors Geometry Lateral Area, Surface Area and Volume

Prisms - definitions A PRISM is any object with two parallel congruent bases with lateral sides that are parallelograms. In this case, the two yellow blue sides are the bases. pink sides The bases are not always on the top and bottom! In the next figure, the bases are the front and the back, because they are the parallel congruent sides.

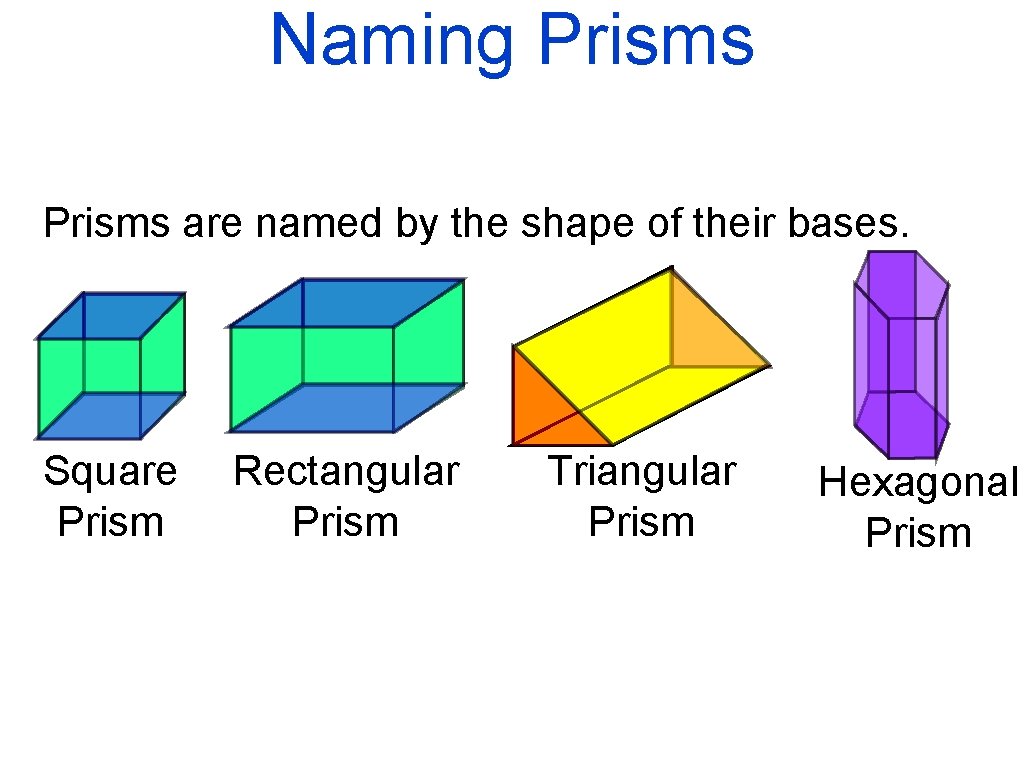
Naming Prisms are named by the shape of their bases. Square Prism Rectangular Prism Triangular Prism Hexagonal Prism

Dog - PRISM

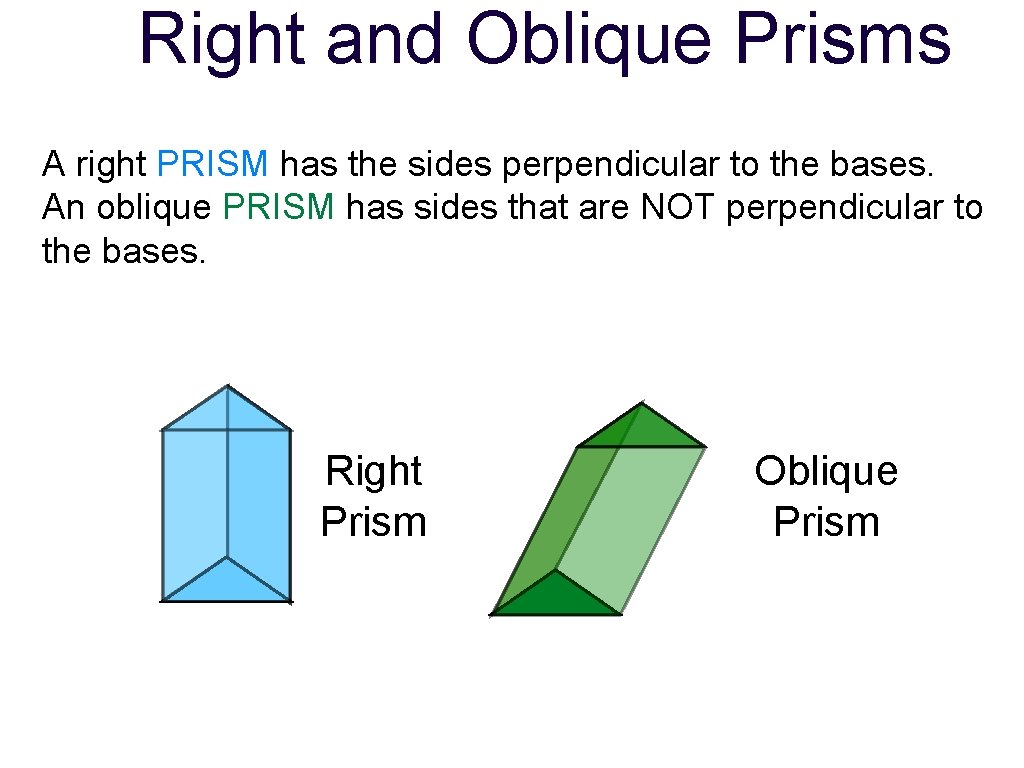
Right and Oblique Prisms A right PRISM has the sides perpendicular to the bases. An oblique PRISM has sides that are NOT perpendicular to the bases. Right Prism Oblique Prism

Cylinders A CYLINDER is a special case of a prism where the two parallel sides (bases) are circles. A cylinder can be thought of as a circular prism. A right cylinder has its side perpendicular to its bases. An oblique cylinder has its side NOT perpendicular to its bases.

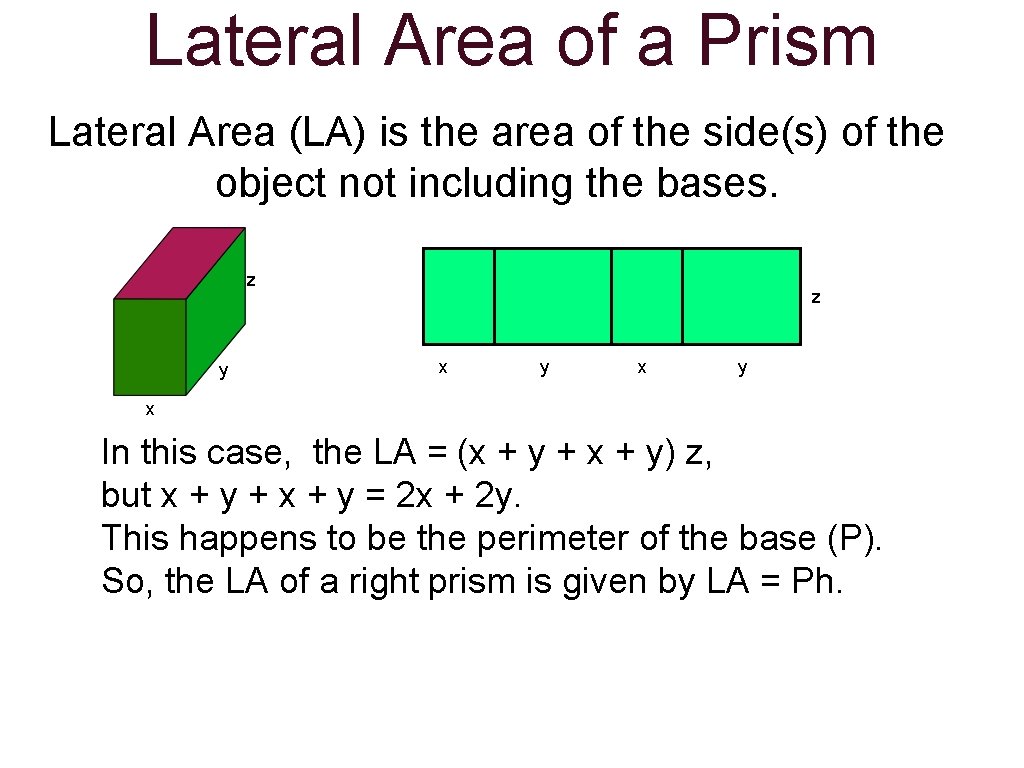
Lateral Area of a Prism Lateral Area (LA) is the area of the side(s) of the object not including the bases. z y z x y x In this case, the LA = (x + y + x + y) z, but x + y + x + y = 2 x + 2 y. This happens to be the perimeter of the base (P). So, the LA of a right prism is given by LA = Ph.

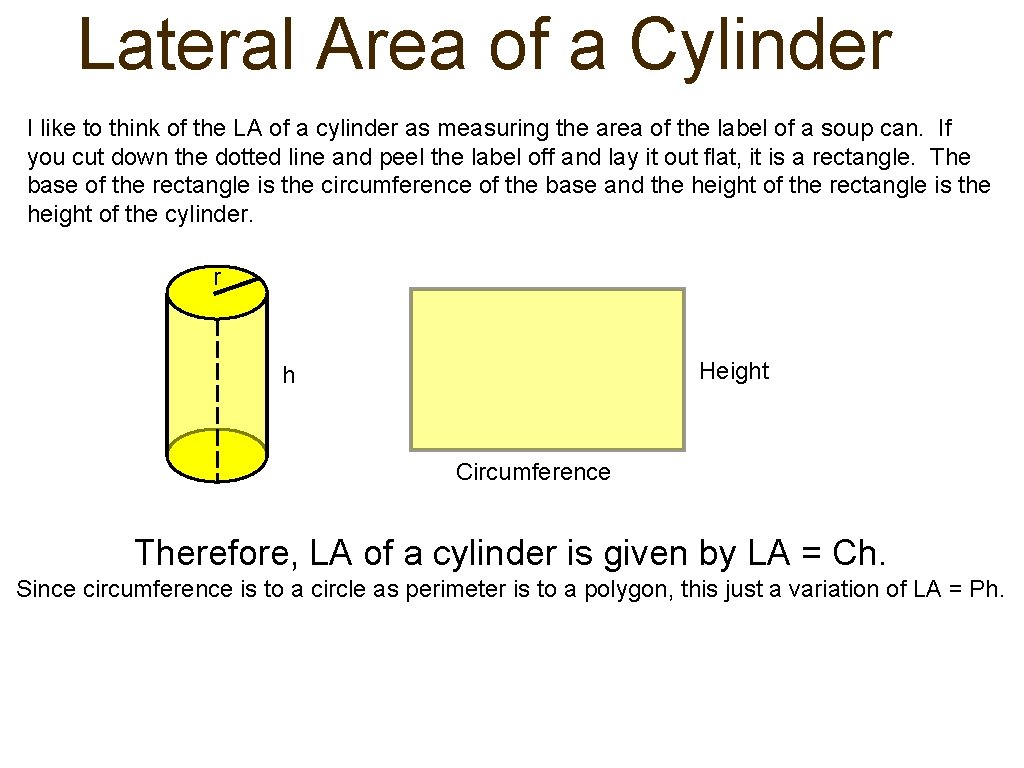
Lateral Area of a Cylinder I like to think of the LA of a cylinder as measuring the area of the label of a soup can. If you cut down the dotted line and peel the label off and lay it out flat, it is a rectangle. The base of the rectangle is the circumference of the base and the height of the rectangle is the height of the cylinder. r Height h Circumference Therefore, LA of a cylinder is given by LA = Ch. Since circumference is to a circle as perimeter is to a polygon, this just a variation of LA = Ph.

Surface (Total) Area of a Prism The Surface area of a Prism is the sum of the area of ALL of the sides. It is also the LA plus the area of the two bases. Since, however the two bases are congruent, the surface area of a right prism (if B is the area of a base) is given by SA = LA + 2 B

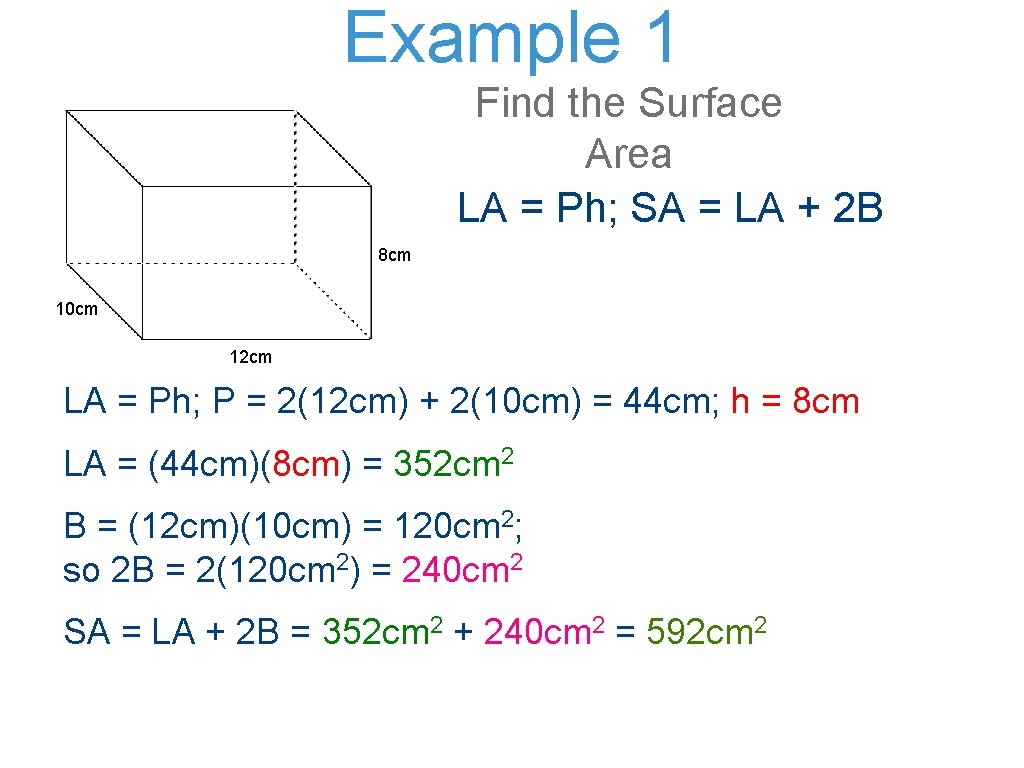
Example 1 Find the Surface Area LA = Ph; SA = LA + 2 B 8 cm 10 cm 12 cm LA = Ph; P = 2(12 cm) + 2(10 cm) = 44 cm; h = 8 cm LA = (44 cm)(8 cm) = 352 cm 2 B = (12 cm)(10 cm) = 120 cm 2; so 2 B = 2(120 cm 2) = 240 cm 2 SA = LA + 2 B = 352 cm 2 + 240 cm 2 = 592 cm 2

Example 2 9 in 12 in 13 in Find the Surface Area LA = Ph; SA = LA + 2 B 15 in LA = Ph; P = 15 in. + 12 in. + 9 in. = 36 in. ; h = 13 in. LA = (36 in. )(13 in. ) = 468 in. 2 B = 1/2(12 in. )(9 in. ) = 54 in. 2; so 2 B = 2(54 in. 2) = 108 in. 2 SA = LA + 2 B = 468 in. 2 + 108 in. 2 = 576 in. 2

Surface Area of a Cylinder The Surface Area of a Cylinder is much like that of a Prism. It the LA + the area of the 2 bases or (since the bases are congruent), LA + twice the area of a base (B). SA = Ch + 2 B

Example 3 Find the Surface Area LA = Ch; SA = LA + 2 B 12 ft r = 8 ft LA = Ch; C = 2π(8 ft. ) = 16π ft. = 50. 27 ft. ; h = 12 ft. LA = (50. 27 ft. )(12 ft. ) = 603. 24 ft. 2 B = π(8 ft. )2 = 64π ft. 2 = 201. 06 ft. 2; so 2 B = 2(201. 06 ft. 2) = 402. 12 ft. 2 SA = LA + 2 B = 603. 24 ft. 2 + 402. 12 ft. 2 = 1005. 36 ft. 2

Assignment Lateral Area and Surface Area all

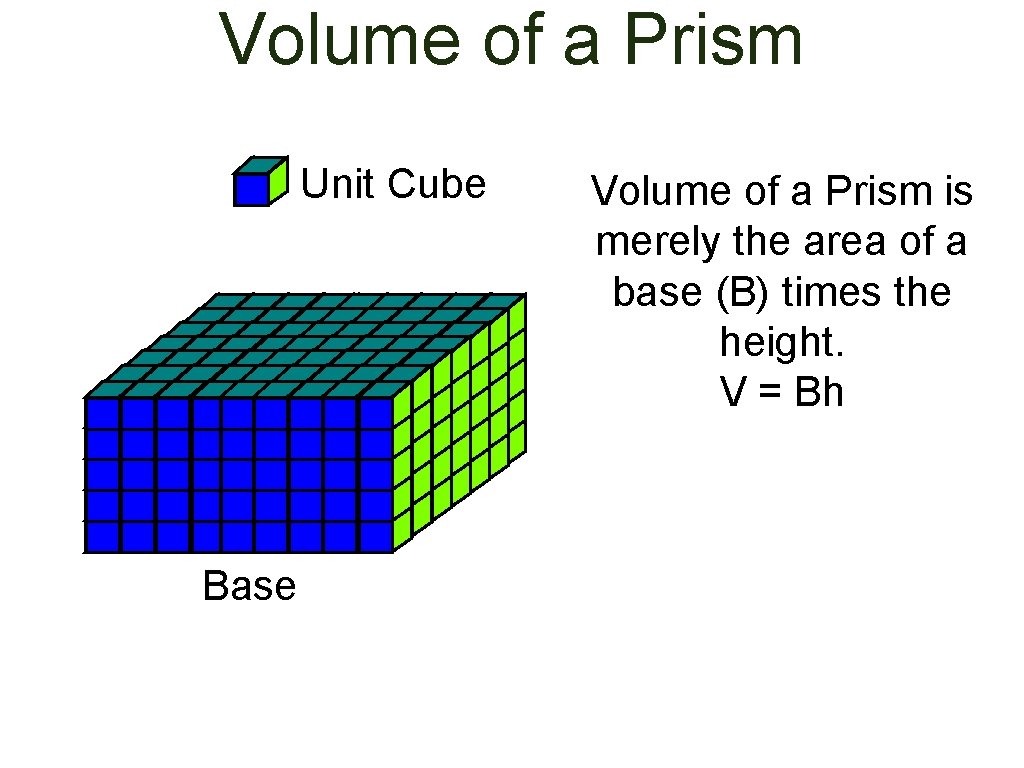
Volume of a Prism Unit Cube Base Volume of a Prism is merely the area of a base (B) times the height. V = Bh

Example 4 Find the Volume 8 cm 10 cm V = Bh 12 cm 2 120 cm B = (12 cm)(10 cm) = h = 8 cm 2 3 V = (120 cm )(8 cm) = 960 cm

Example 5 9 in 12 in Find the Volume 13 in V = Bh 15 in B = 1/2(12 in)(9 in) = 54 in 2 h = 13 in. V = (54 in 2)(13 in) = 702 in 3

Volume of a Cylinder Like a prism, the volume of a Cylinder is the area of a base times its height. V = Bh

Example 6 Find the Volume 12 ft r = 8 ft V = Bh B = π(8 ft)2 = 64π 2 ft h = 12 ft V = (64π ft 2)(12 ft) = 768π ft 2 = 2412. 74 ft 2

Assignment Volume - all

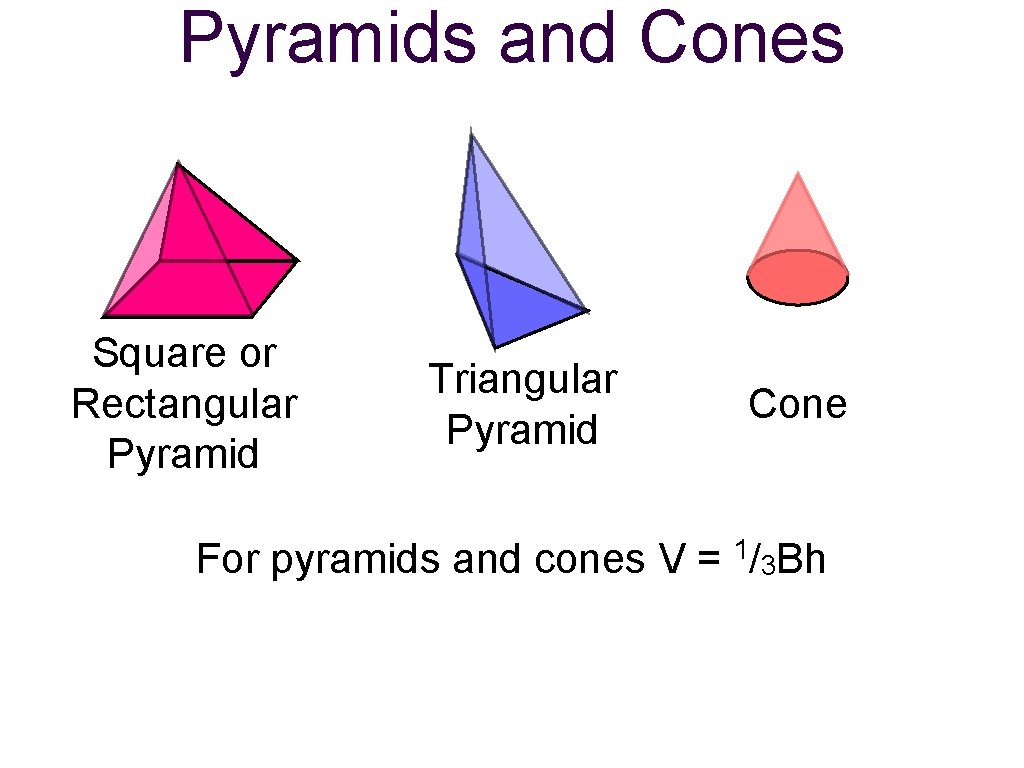
Pyramids and Cones Square or Rectangular Pyramid Triangular Pyramid For pyramids and cones V = Cone 1/ 3 Bh

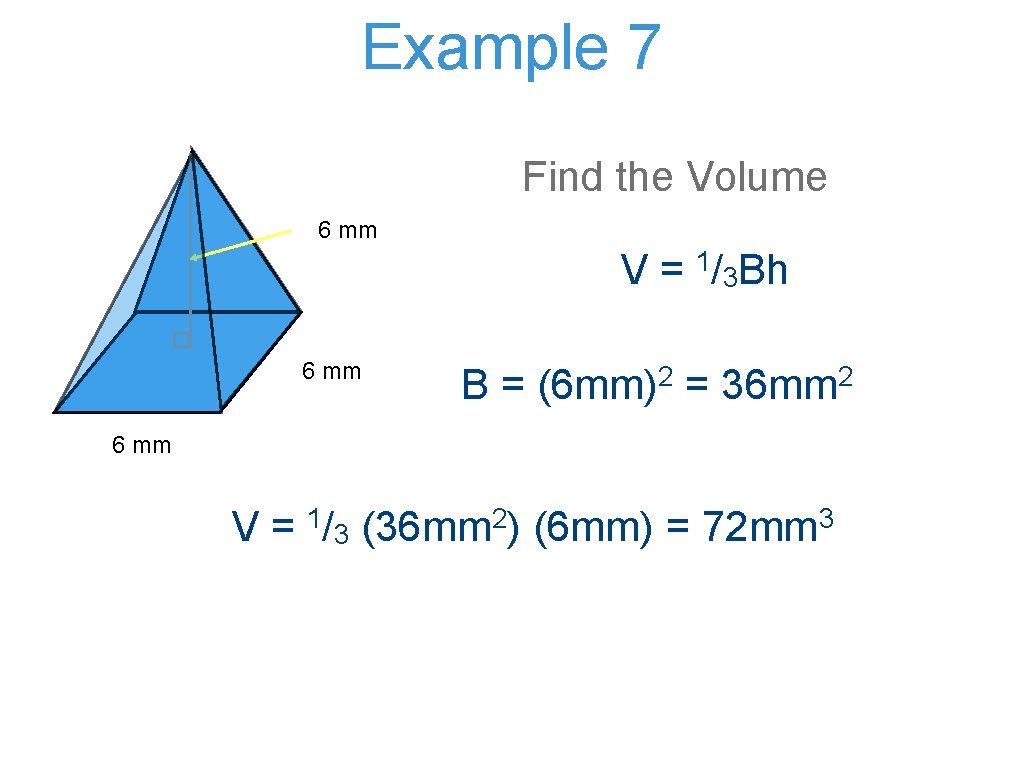
Example 7 Find the Volume 6 mm V= 6 mm 1/ 3 Bh B = (6 mm)2 = 36 mm 2 6 mm V= 1/ 3 2 (36 mm ) (6 mm) = 3 72 mm

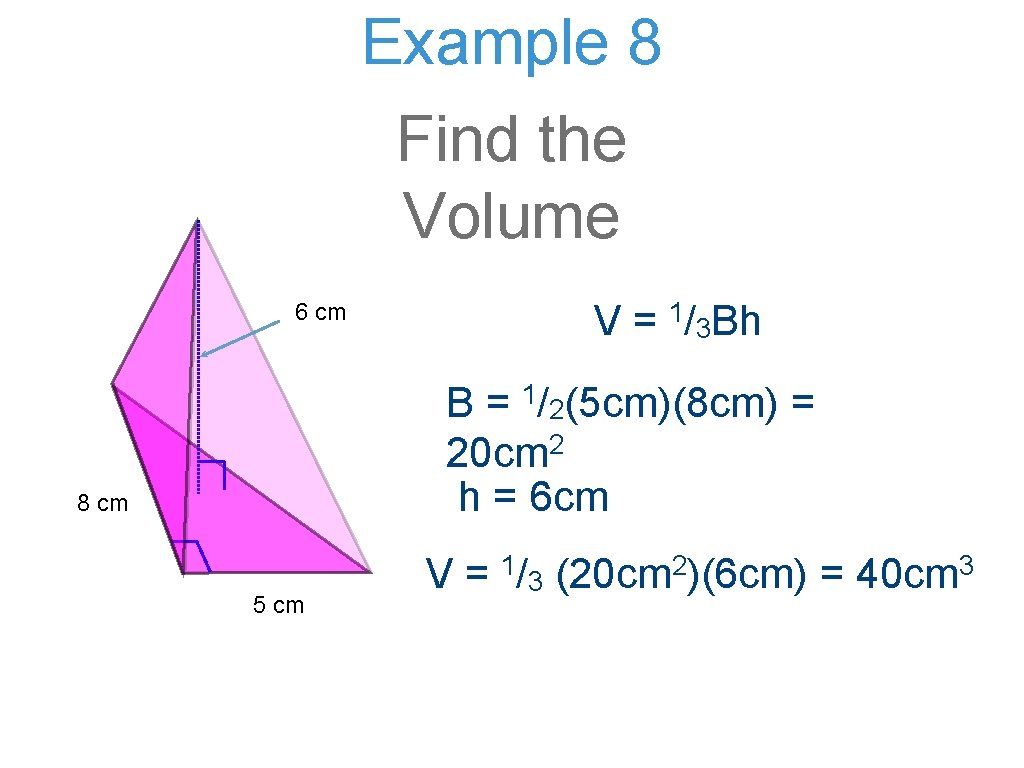
Example 8 Find the Volume V = 1/3 Bh 6 cm 1/ B = 2(5 cm)(8 cm) = 20 cm 2 h = 6 cm 8 cm 5 cm V= 1/ 3 2 (20 cm )(6 cm) = 3 40 cm

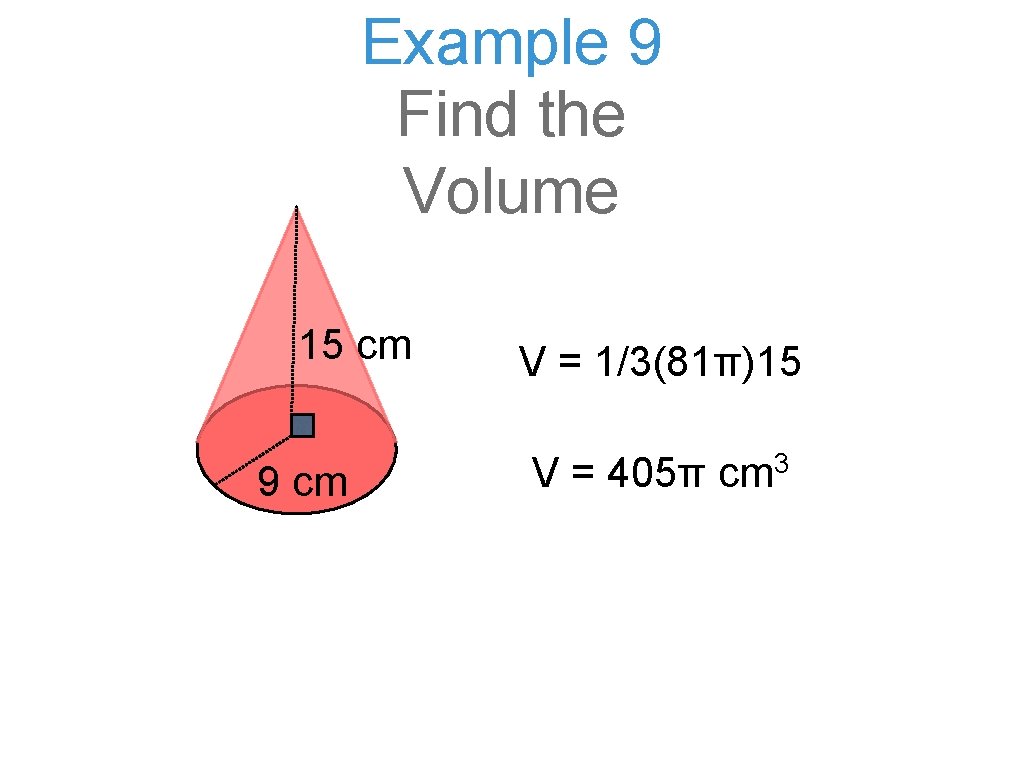
Example 9 Find the Volume 15 cm 9 cm V = 1/3(81π)15 V = 405π cm 3

Assignment Pyramids and Cones - all

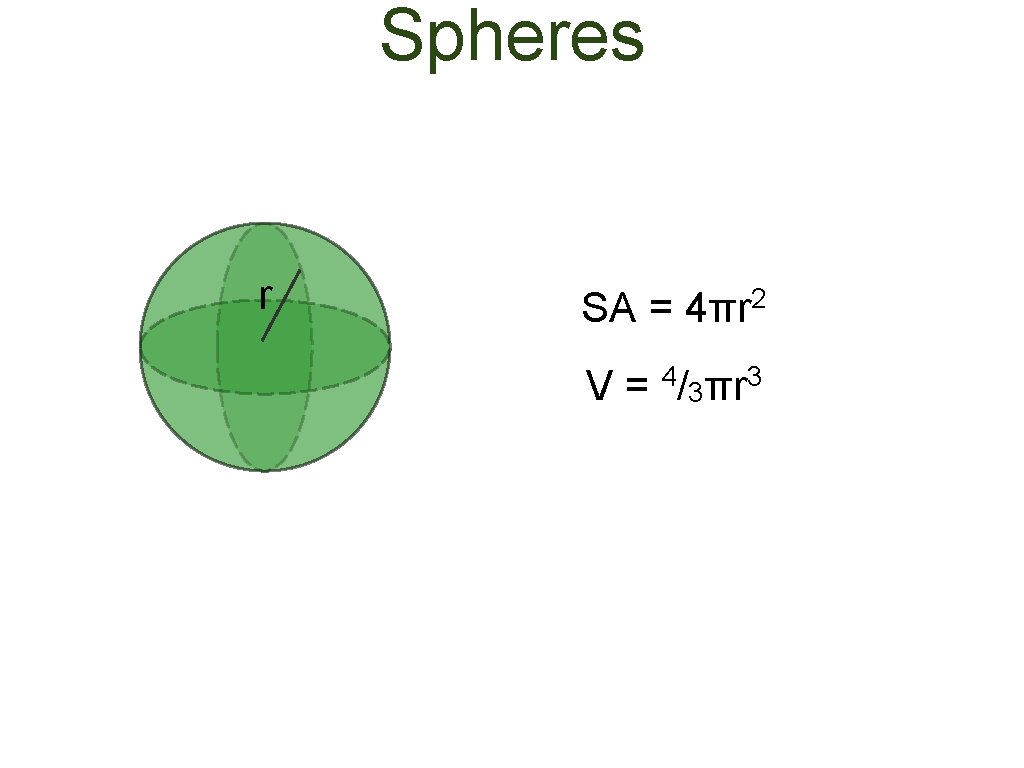
Spheres r SA = 4πr 2 V = 4/3πr 3

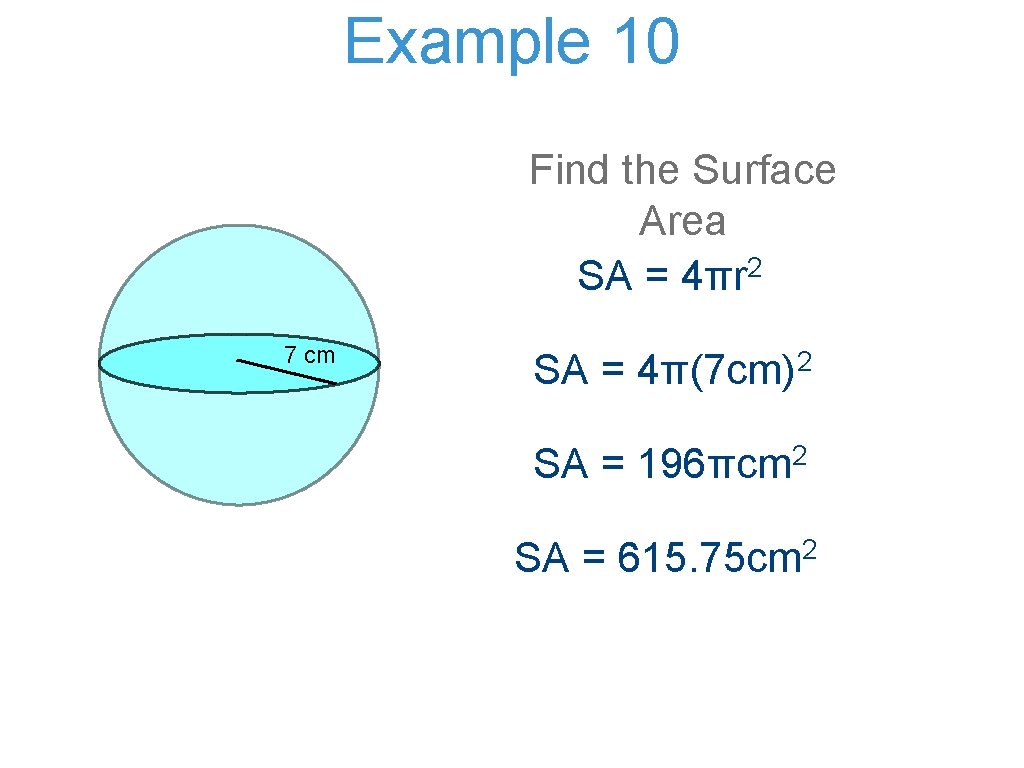
Example 10 Find the Surface Area SA = 4πr 2 7 cm SA = 2 4π(7 cm) SA = 196πcm 2 SA = 2 615. 75 cm

Example 11 Find the Volume V= 12 cm 4/ 3 3 πr V = 4/3π(12 cm)3 V = 2304πcm 3 V= 3 7238. 23 cm

Assignment Spheres - all