Homology and Substitution matrices CSCI 6904 Multiple sequence

Homology and Substitution matrices CSCI 6904

Multiple sequence alignment problem local Search / Global Search problem How to Quantify equivalence for the purpose of scoring?
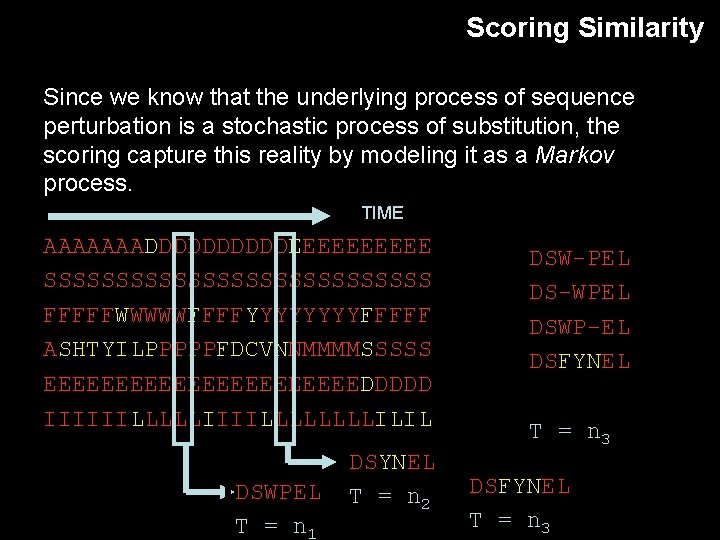
Scoring Similarity Since we know that the underlying process of sequence perturbation is a stochastic process of substitution, the scoring capture this reality by modeling it as a Markov process. TIME AAAAAAADDDDDEEEEE SSSSSSSSSSSSSS FFFFFWWWWWFFFFYYYYFFFFF ASHTYILPPPPPFDCVNNMMMMSSSSS EEEEEEEEEEEDDDDD IIIIIILLLLLLLLILIL DSWPEL T = n 1 DSYNEL T = n 2 DSW-PEL DS-WPEL DSWP-EL DSFYNEL T = n 3

Scoring Similarity Not all substitution will be equally good. Organism eonciding a gene with an inappropriate substitution may be eliminated by purifying selection. The “appropriatedness” is determined on a case by case basis. Although general trends exists. TIME AAAAAAADDDDDEEEEE SSSSSSSSSSSSSS FFFFFWWWWWFFFFYYYYFFFFF ASHTYILPPPPPFDCVNNMMMMSSSSS EEEEEEEEEEEDDDDD IIIIIILLLLLLLLILIL DSWPEL T = n 1 DSYNEL T = n 2 DSW-PEL DS-WPEL DSWP-EL DSFYNEL T = n 3

Scoring Similarity Matrices are capturing these general trends. TIME AAAAAAADDDDDEEEEE SSSSSSSSSSSSSS FFFFFWWWWWFFFFYYYYFFFFF ASHTYILPPPPPFDCVNNMMMMSSSSS EEEEEEEEEEEDDDDD IIIIIILLLLLLLLILIL DSWPEL T = n 1 DSYNEL T = n 2 DSW-PEL DS-WPEL DSWP-EL DSFYNEL T = n 3

Scoring Similarity For nucleotides there a limited number of substitutions A C G T The simplest model assumes a uniform substitution process A G T C A 0. 99 G 0. 033 0. 99 T 0. 033 0. 99 C 0. 033 0. 99

Scoring Similarity For nucleotides there a limited number of substitutions A C G T Or some more biological facts that can be added to the model. A G T A 0. 99 G 0. 06 0. 99 T 0. 02 0. 99 C 0. 02 0. 06 C 0. 99

Scoring Similarity For nucleotides there a limited number of substitutions A C G T It may even be safe to estimate many/all parameters from the data. A G T A 1 -a-2 b G a 1 -a-2 b T b b 1 -a-2 b C b b a C 1 -a-2 b

Log odd-ratio For nucleotides, there a limited number of substitutions Where Mij is taken from such table of sustitutions. Mij is sensitive to distance, so will be these.
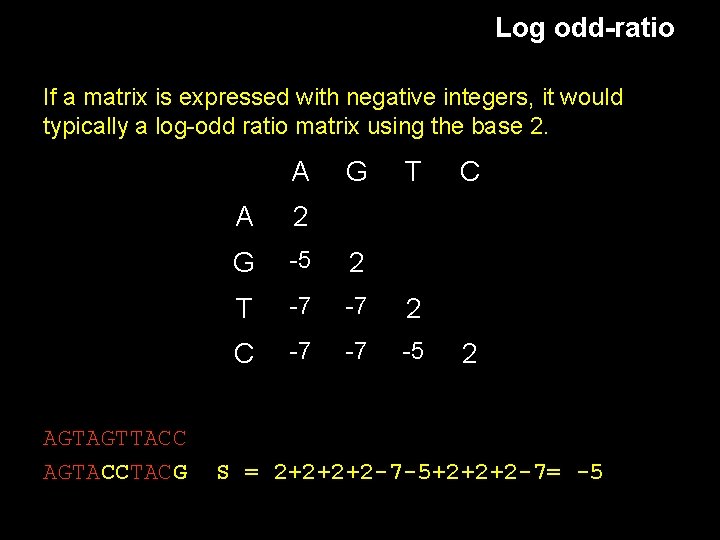
Log odd-ratio If a matrix is expressed with negative integers, it would typically a log-odd ratio matrix using the base 2. A AGTAGTTACC AGTACCTACG G T A 2 G -5 2 T -7 -7 2 C -7 -7 -5 C 2 S = 2+2+2+2 -7 -5+2+2+2 -7= -5

Empirical Substitution Matrices To generate a statistically robust matrix, there must be a large amount of data to compile. This is not generally the case. For this reason, there are some generic matrices available. We’ll have a look at them, and how they are derived.

Empirical Substitution matrices PAM Point Accepted Mutation amongst (pairwise) closely related sequences. BLOSUM Compiled from BLOCKS of aligned sequences.

PAM, How it happened Basic Matrix 1 PAM -> 1% Point accepted mutations Extrapolation 2 – 512 PAM What “Accepted” means? The principle is that the mutation observed in highly similar (1% identity) are going to be “neutral”. Therefore, this is assume to quantify characters equivalence. Point mutations assumed i -> j (good) i -> k -> j (assumed not to happen in closely related sequences)

PAM, How it happened Given a basic, trusted alignment AAAB ABAB AAAA Align all possible pairs of sequence and compile the transitions.

PAM, How it happened Compiled transitions: (assumes symmetry) Mutability: Substitution:

PAM, How it happened Compiled transitions: Will give a matrix of probability of observing substitutions I -> j for closely related sequences.

Extrapolating PAM We can obtain Mij for any multiple of PAM 1 by doing a matrix multiplication.

Extrapolating PAM If 1 can be regarded as an “instant rate”, it is possible to approximate a matrix of substitution for arbitrary distances (multiple of our “instant rate”).

Extrapolating PAM Assymptotically Interpretation Although built from a collection of “minor” changes, the process is truly Markovian and converge toward the equilibrium frequencies.

Extrapolating PAM 20 Great for scoring closely related sequences and detecting high level of sequence identity. PAM 250 Appropriate to evaluate long sequences of low character identity.

Why using PAM over edit distance? Log-odd ratio tables can be generated as previously described for generating fast scoring matrices. 1. 2. Considers the biological reality of each characters Considers the context of the string analyzed, and that the scoring scheme has a dependence with evolutionary distance.

BLOSUM, How it happened Basic Matrix BLOSUMX, X refers to the “tightness” of reference dataset in percent points. Extrapolation 100 - 1 BLOCK? Make an alignment using an identity criterion. Splice regions of ambiguous alignment. Work with the “trusted” left-overs.

BLOSUM, How it happened Given a basic, trusted alignment BABA AAAC AACC AABA AACC AABC

Practical issues and difference between the two methods Reference sets and real data The appropriateness of a matrix to a specific problem depends on whether the data of interest would have been included in the reference set in the first place (This is especially true for BLOSUM). BLOSUM 45 , BLOSUM 62, BLOSUM 80 were compiled with block having at least X% of sequence identity. BLOSUM thus does not exclude i -> k -> j processes while the observation is i -> j. BLOSUM does not implicitly assume that i -> j is “neutral”.

Availability http: //www. genome. ad. jp/

Reference reading for next section Setubal and Meidanis, Introduction to Computational Molecular Biology, Brook Coles Publishing, Pacific Cove, CA, USA. 1997, ISBN 0 -534 -95262 -3

Aligning two sequences ATC vs AGTC Use of dynamic programming to trace a path between two sequences. A T C 0 -2 -2 -2 A -2 1 -1 -1 G -2 -1 -1 -1 T -2 -1 1 -1 C -2 -1 -1 1

Aligning two sequences ATC vs AGTC A-TC AGTC A T C 0 -2 -4 -6 A -2 1 -1 -3 G -4 -1 0 -2 T -6 -3 1 -1 C -8 -5 -1 2

Aligning two sequences ATC vs AGTC A-TC AGTC A T C 0 -2 -4 -6 A -2 1 -1 -3 G -4 -1 0 -2 T -6 -3 1 -1 C -8 -5 -1 2 Semi-global variation Do not apply a gap penalty before and after the first and last characters.

Aligning two sequences Given the alignment: ATCTGTATTTGGACATGATCGTGATAGC…TTAGTCGGA ATCTGCATG----------…---GTCGGA The following alignment would not be surprising (providing a sufficiently long insertion): ATCTGTATTTGGACATGATCGTGATAGC…TTAGTCGGA ATCTGCATG-G----T---CG-GA----…----Although it is almost certain that the first alignment represents better what really happened.
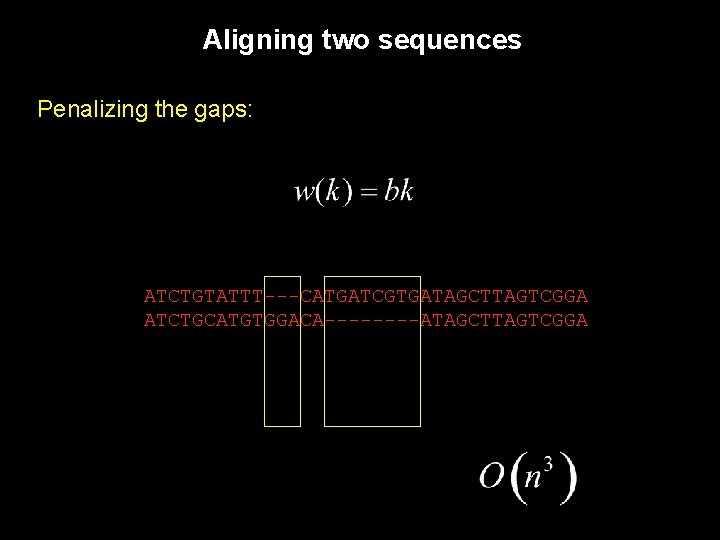
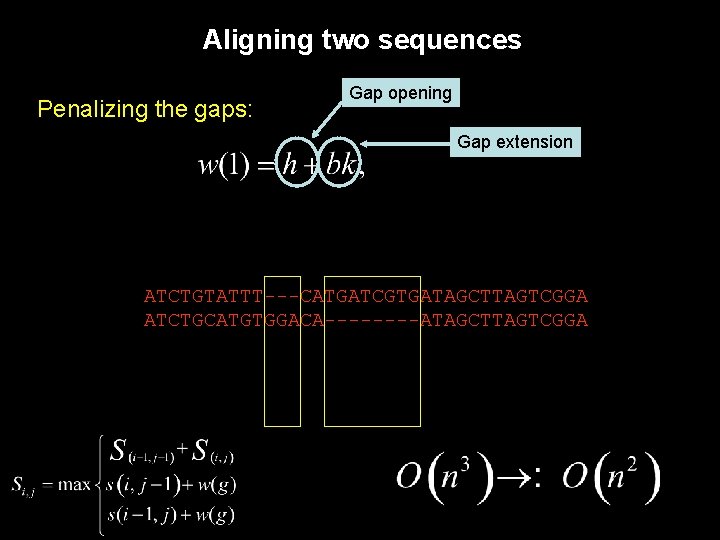
Aligning two sequences Penalizing the gaps: ATCTGTATTT---CATGATCGTGATAGCTTAGTCGGA ATCTGCATGTGGACA----ATAGCTTAGTCGGA
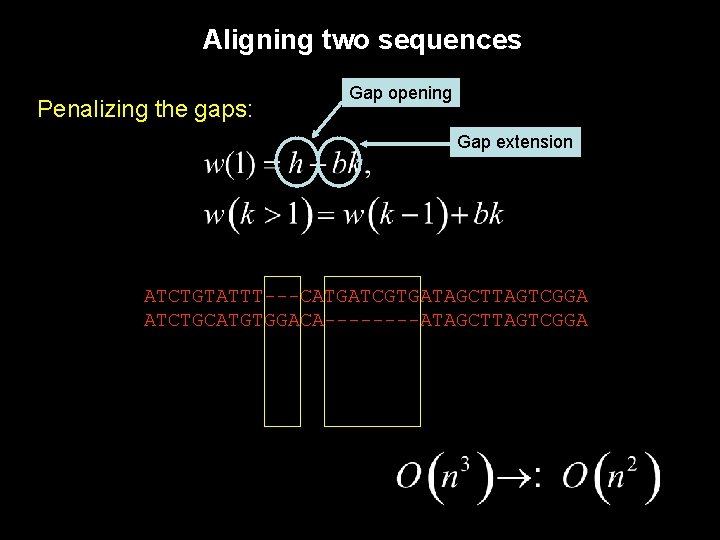
Aligning two sequences Penalizing the gaps: Gap opening Gap extension ATCTGTATTT---CATGATCGTGATAGCTTAGTCGGA ATCTGCATGTGGACA----ATAGCTTAGTCGGA

Searching a database for homologous sequences String search with in mind the process under which these strings were generates (evolution) FASTA Heuristics based on k-tuples matching BLAST (BLAST 2, PSI-BLAST, …) Heuristics based on w-tuples matching

FASTA 1988 – accelerated biological sequence searches by 10 -100 times vs. dynamic programming Sliding window of substring of Q along the S (database) These are defined as tuple of length k, or k-tuples.

FASTA 1988 – accelerated biological sequence searches by 10 -100 times vs. dynamic programming Ten best-scoring regions in edit distance may not be the 10 best scoring sequences using a scoring matrix
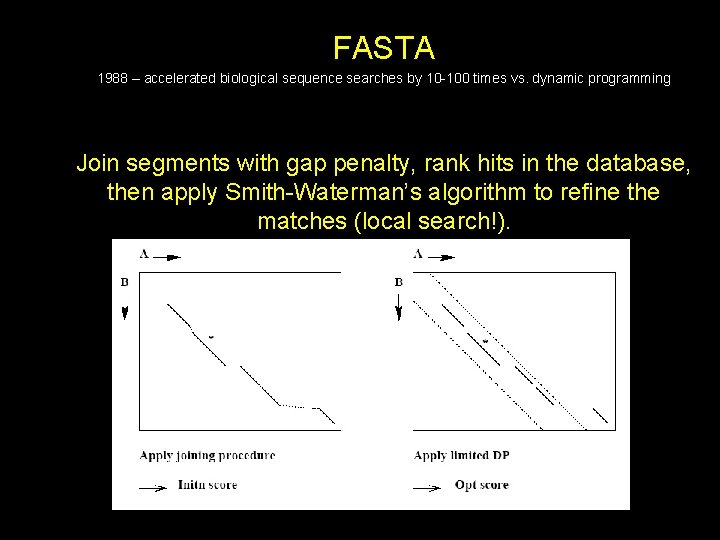
FASTA 1988 – accelerated biological sequence searches by 10 -100 times vs. dynamic programming Join segments with gap penalty, rank hits in the database, then apply Smith-Waterman’s algorithm to refine the matches (local search!).

BLAST The most popular homology-based search algorithm. Heuristic w-tuple search for candidates With an improvement from FASTA at the implementation level Statistical validation based on expected score from random walk. Pretty cool

BLAST The most popular homology-based search algorithm. Pre-processing Generate all possible word of length w, given an alphabet, into vector W. For each position p in Q (query sequence), derive a word w(p) and record a list of words of W which score better than a threshold T using something like edit distance. These will be called neighbors list. We are assuming that this word indexing has been done on the database D earlier. Find any position p in D which have a common word in the neighbors list with the query Q. These will be called “hits”.

BLAST The most popular homology-based search algorithm. Extension of hits into HSP Each hit will be extended in both direction to determine the full length of the matches. The extension will stop once the score of the alignment will drop below a certain threshold. The Maximum score, and the length of the alignment will be recorded and used to evaluate the statistical significance of the overall alignment.

BLAST Foundation Random Walk By scoring the match / mis-match along the alignment of substrings. Test Statistic By determining the significance of an “excursion” between two successful runs.

BLAST The most popular homology-based search algorithm. Extension of hits into HSP Each hit will be extended in both direction to determine the full length of the matches. The extension will stop once the score of the aligment will drop below a certain threshold. The Maximum score, and the length of the alignment will be recorded and used to evaluate the statistical significance of the alignment.
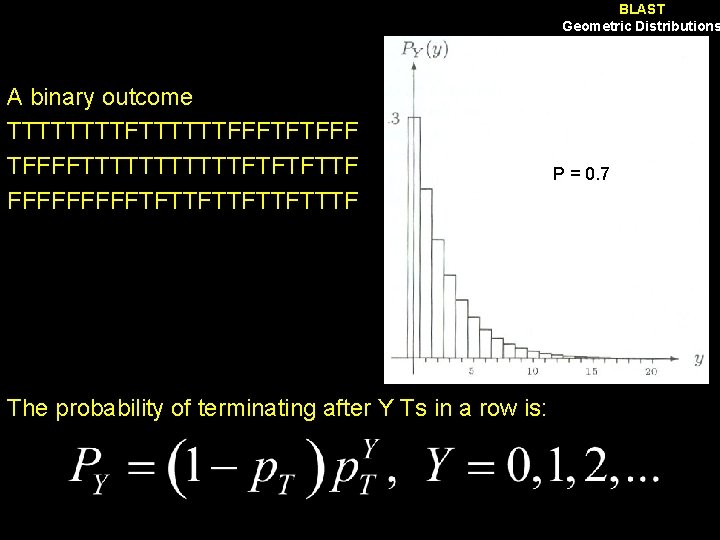
BLAST Geometric Distributions A binary outcome TTTTFTTTTTTFFFTFTFFFFTTTTTTFTFTFTTF FFFFFTFTTFTTTF The probability of terminating after Y Ts in a row is: P = 0. 7

BLAST Random Walks Principle Start at h = 0 Stop at a = -1 Artificial upper bound “b” Evaluate: Probability of observing peak height B Probability of observing such excursion length
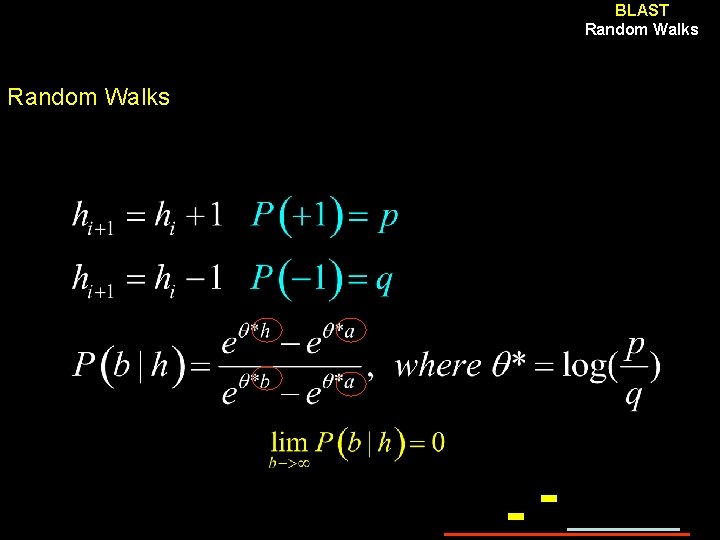
BLAST Random Walks

BLAST Random Walks For arbitrary scoring schemes: Ultimately:

BLAST Random Walks

BLAST Principle Statistics Test Statistic 1 – By determining the expected number of random match with a equal or better score S within the whole database: 2 – By determining the probability of finding n other HSP is thus (though will not be demonstrated!):

BLAST Principle Test Statistic 1 – By determining the expected number of random match with a equal or better score S within the whole database: 2 – By determining the probability of finding no other HSP is thus:

BLAST Principle Test Statistic 1 – By determining the expected number of random match with a equal or better score S within the whole database: 2 – By determining the probability of finding one other HSP is thus:
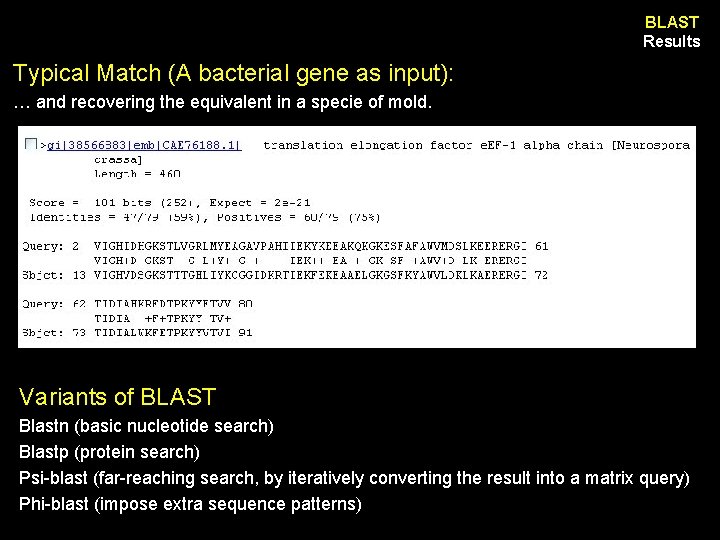
BLAST Results Typical Match (A bacterial gene as input): … and recovering the equivalent in a specie of mold. Variants of BLAST Blastn (basic nucleotide search) Blastp (protein search) Psi-blast (far-reaching search, by iteratively converting the result into a matrix query) Phi-blast (impose extra sequence patterns)

Multiple Sequence alignment We know why sequences are aligning together: physical basis

Aligning two sequences ATC vs AGTC Use of dynamic programming to trace a path between two sequences. A T C -2 -2 -2 A -2 +1 -1 -1 G -2 -1 -1 -1 T -2 -1 +1 -1 C -2 -1 -1 0 +1 For protein, these entries would be scores from a matrix such as PAM, BLOSUM, JTT…

Aligning two sequences ATC vs AGTC Score in the matrix are determined by: A-TC AGTC A T C 0 -2 -4 -6 A -2 1 -1 -3 G -4 -1 0 -2 T -6 -3 1 -1 C -8 -5 -1 2 And then backtracking to find the optimal path from the lower right to upper left corner of the matrix.

Aligning two sequences Without penalizing gaps, strange behavior can occur: ATCTGTATTTGGACATGATCGTGATAGC…TTAGTCGGA ATCTGCATG----------…---GTCGGA The following alignment would not be surprising (providing a sufficiently long insertion): ATCTGTATTTGGACATGATCGTGATAGC…TTAGTCGGA ATCTGCATG-G----T---CG-GA----…----Although it is almost certain that the first alignment represents better what really happened.
Aligning two sequences Penalizing the gaps: Gap opening Gap extension ATCTGTATTT---CATGATCGTGATAGCTTAGTCGGA ATCTGCATGTGGACA----ATAGCTTAGTCGGA
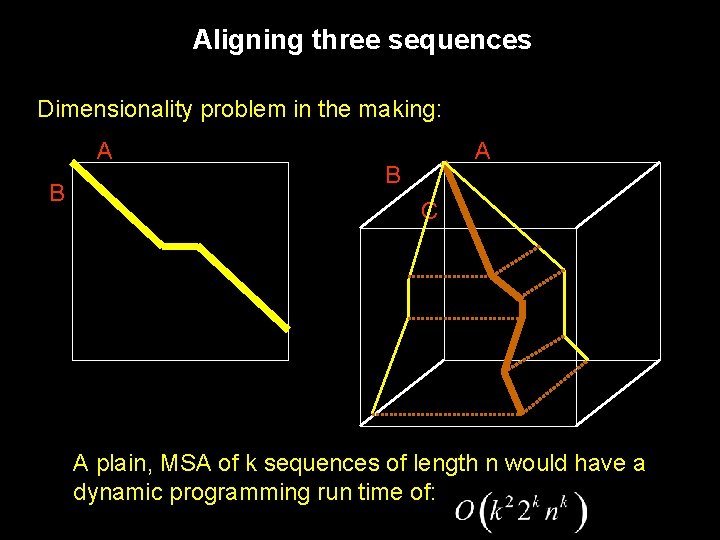
Aligning three sequences Dimensionality problem in the making: A B C A plain, MSA of k sequences of length n would have a dynamic programming run time of:
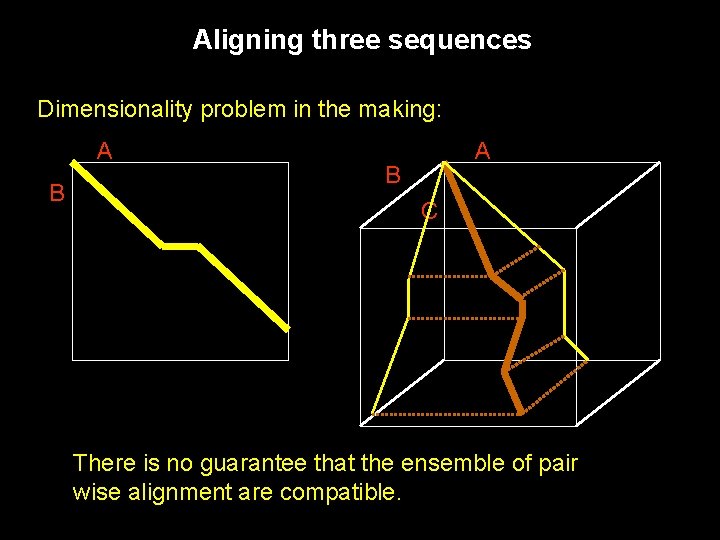
Aligning three sequences Dimensionality problem in the making: A B C There is no guarantee that the ensemble of pair wise alignment are compatible.
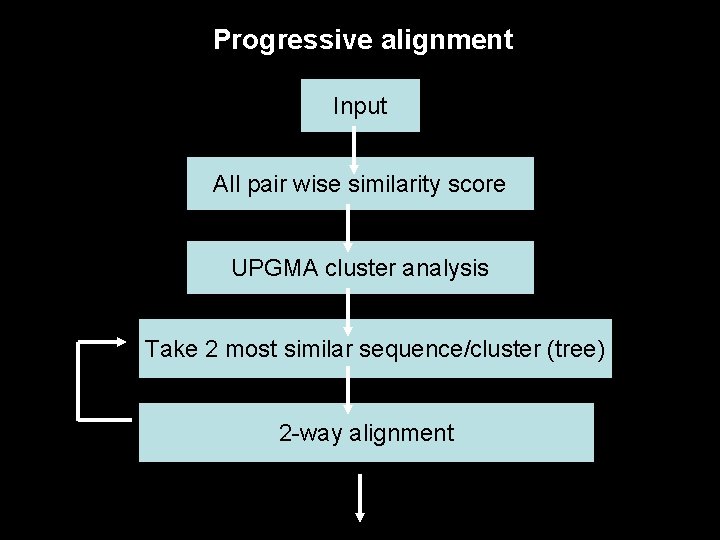
Progressive alignment Input All pair wise similarity score UPGMA cluster analysis Take 2 most similar sequence/cluster (tree) 2 -way alignment

Progressive alignment Given a number n of related sequences: S 1 S 2 S 3 S 4 S 2 Whose relations can be represented by a tree: S 4 S 1 S 3
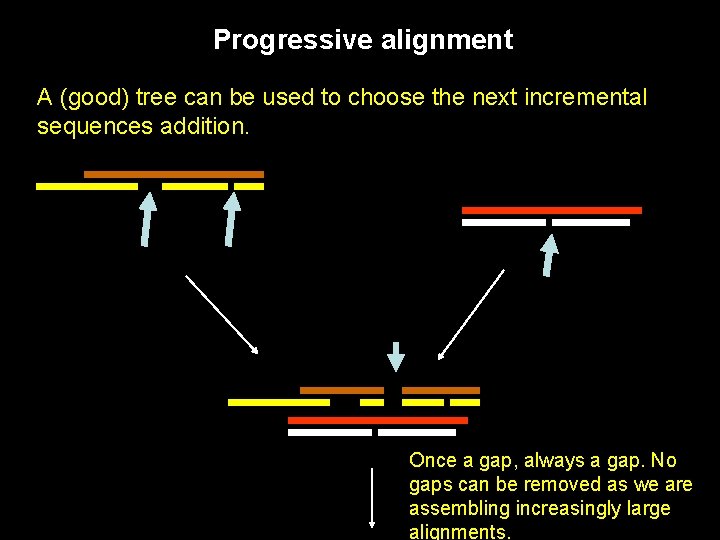
Progressive alignment A (good) tree can be used to choose the next incremental sequences addition. Once a gap, always a gap. No gaps can be removed as we are assembling increasingly large alignments.

Progressive alignment Sum-of-pairs (SP) 1. Scoring scheme when there are multiple sequences to align. 2. This will run in O(k 2) to calculate the SP score.

Progressive alignment Sum-of-pairs (SP) 1. Score is independent of the input sequence order. 2. This will run in O(k 2) to calculate the SP score.

The most important thing that can be done with aligned sequence is to discover their mutual relationships.

The discipline that is interested in reconstructing the past using a collection of contemporary observations is called phylogeny.
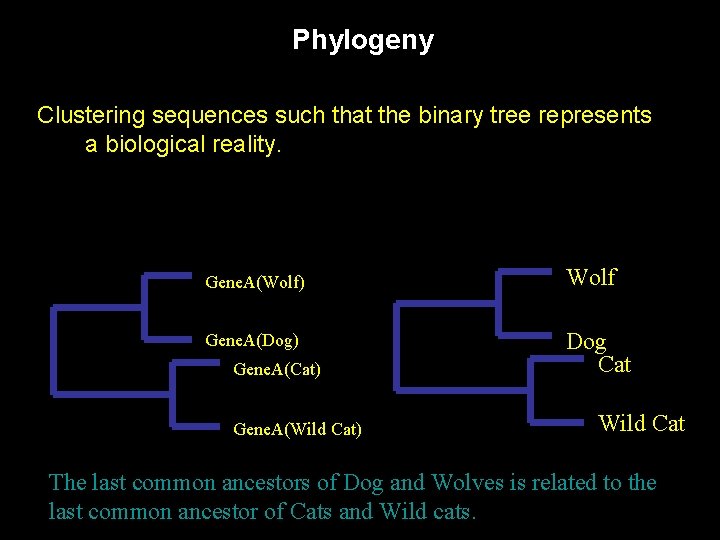
Phylogeny Clustering sequences such that the binary tree represents a biological reality. Gene. A(Wolf) Wolf Gene. A(Dog) Dog Cat Gene. A(Cat) Gene. A(Wild Cat) Wild Cat The last common ancestors of Dog and Wolves is related to the last common ancestor of Cats and Wild cats.
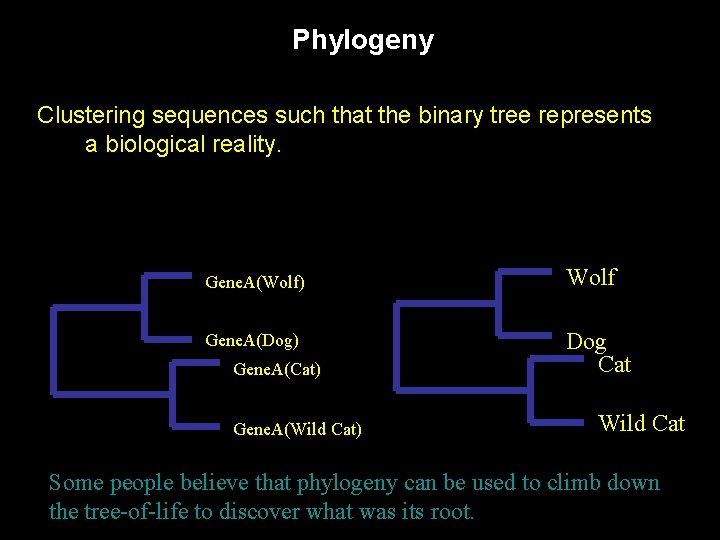
Phylogeny Clustering sequences such that the binary tree represents a biological reality. Gene. A(Wolf) Wolf Gene. A(Dog) Dog Cat Gene. A(Cat) Gene. A(Wild Cat) Wild Cat Some people believe that phylogeny can be used to climb down the tree-of-life to discover what was its root.
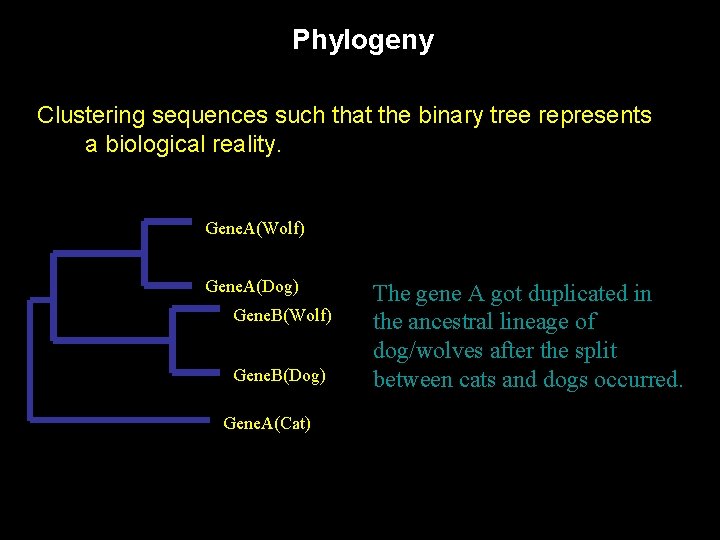
Phylogeny Clustering sequences such that the binary tree represents a biological reality. Gene. A(Wolf) Gene. A(Dog) Gene. B(Wolf) Gene. B(Dog) Gene. A(Cat) The gene A got duplicated in the ancestral lineage of dog/wolves after the split between cats and dogs occurred.

Phylogeny reconstitute events that occurred in the past. Fossil records can be used, but these are rare and are likely to contain less information that a sequence would (Subjectivity of comparing continuous characters amongst many other things). Principle Since sequences are evolving via a stochastic process. The more different two sequences are, the longest should be the time expended since they shared a common ancestor.

Phylogeny Principle Since sequences are evolving via a stochastic process. The more different two sequences are, the longest should be the time expended since they shared a common ancestor. Technically, with the knowledge of the generating process, solving phylogeny can be abstracted to a clustering problem.

Phylogeny Definitive reference / introduction Felsenstein, J. 2004. Inferring Phylogenies, Sinauer Assoc. , Sunderland, MA, USA. 664 pages. – – Inclusive theoretical approaches Software implementations (brief, but there)

Phylogeny Strategies Discrete character approaches Parsimonious criterion Model likelihood criterion Hypothesis likelihood criterion Distance-based clustering Least-square Neighbor-Joining / UPGMA (Implicit topology) Minimum Evolution

Phylogeny Distance-based strategies UPGMA method Assumes a “molecular clock” (ie. : All sequences evolved at the same rate and therefore root of a branch is located at the midpoint between each pairs of sequences). Requires an arbitrary measure of “distance”. (ie. : You throw away the sequence information prior to clustering)

UPGMA algorithm Input: M, a n 2 matrix of pair wise distances Output: T, a binary tree relating n elements. 1: Find smallest M(i, j) entry 2: Create new element ij 3: Connect Element i and j to ij and set M(I, ij) = M(j, ij) = M(i, j) / 2 to form T 4: For all non i and j elements: Compute: 5: Delete the rows and columns for i and j. 6: Add a row and column for ij 7: if M has only 1 element: Return T else: Goto 1

UPGMA algorithm Computational time of about: Or 2 n 2 if the algorithm keep tracks and update a list of small entries over n rows.

UPGMA’s shortcoming “Molecular Clock” assumption can be rejected in most cases. In this example, un-equally evolving sequences are clustering according to their rate of evolution rather than according to the history of the genes.
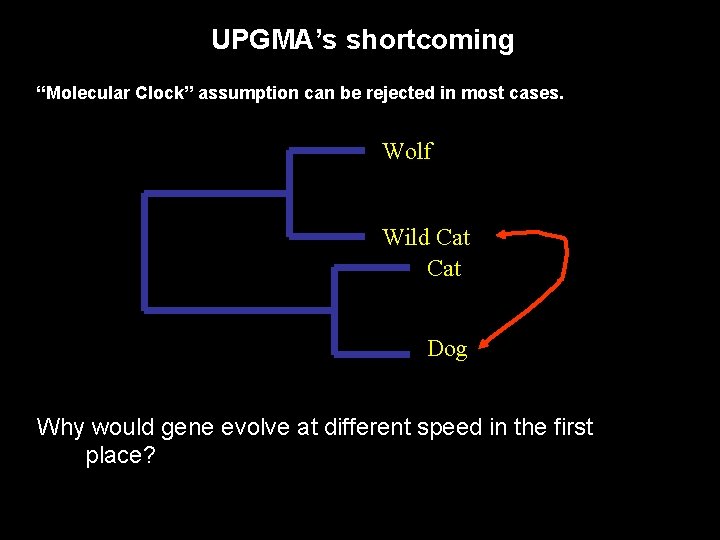
UPGMA’s shortcoming “Molecular Clock” assumption can be rejected in most cases. Wolf Wild Cat Dog Why would gene evolve at different speed in the first place?

Rate of evolution Technically, the “evolution” is the result of a random DNA perturbation process. – – – Mutagenic agents Copy errors (mainly) Radiations The basal rate of evolution thus should be relatively constant for organism living in similar environment. However, the most time-critical a gene is, the more likely it is to be constrained into its precise sequence. Selection thus is responsible for what we observes as rate of evolution.

A word on natural Selection The idea that evolution is intended as a process of optimization is wrong. The random process of altering the sequence on DNA is essentially a destructive process. à Stochastic perturbation in a delicately balanced system is bound in the long run to decay the fitness of the gene, and thus the organism. à Meanwhile, this “force” is responsible to generate a range of variability around a fit solution. [Neutral Evolution] à If one of these alternative solution is especially bad, it prevents the host organism from reproducing. à If the living conditions change (see this as altering the objective function), the fittest solution will necessarily change providing that there is enough diversity in a population.
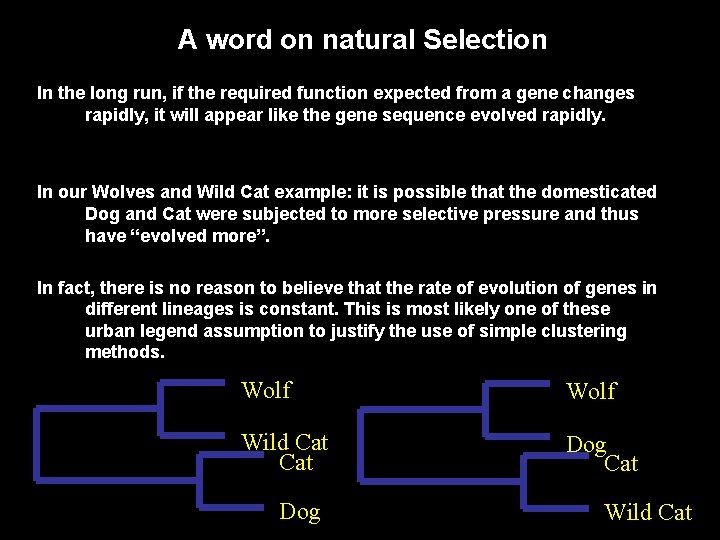
A word on natural Selection In the long run, if the required function expected from a gene changes rapidly, it will appear like the gene sequence evolved rapidly. In our Wolves and Wild Cat example: it is possible that the domesticated Dog and Cat were subjected to more selective pressure and thus have “evolved more”. In fact, there is no reason to believe that the rate of evolution of genes in different lineages is constant. This is most likely one of these urban legend assumption to justify the use of simple clustering methods. Wolf Wild Cat Dog Wild Cat

Neighbor-Joining algorithm Guarantee to recover the true tree if the distance matrix is an exact reflection of the tree. Popular methods, its fast and it implicitly recover a tree topology.
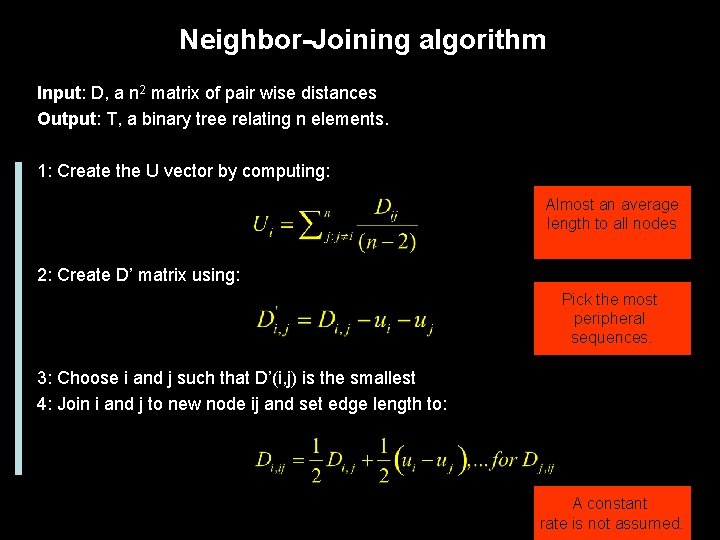
Neighbor-Joining algorithm Input: D, a n 2 matrix of pair wise distances Output: T, a binary tree relating n elements. 1: Create the U vector by computing: Almost an average length to all nodes 2: Create D’ matrix using: Pick the most peripheral sequences. 3: Choose i and j such that D’(i, j) is the smallest 4: Join i and j to new node ij and set edge length to: A constant rate is not assumed.

Neighbor-Joining algorithm (contn’d… ) Input: D, a n 2 matrix of pair wise distances Output: T, a binary tree relating n elements. 5: Compute distances between all nodes k and node ij: 6: Delete from D matrix i and j entries, add ij 7: If dimension of D > 2 X 2: Goto 1

Neighbor-Joining algorithm Guarantee to recover the true tree if the distance matrix is an exact reflection of the tree. How realistic is it to assume that these distances are behaving as such?
- Slides: 83