Homographic Functions avril 09 Homographic Functions 1 Basic

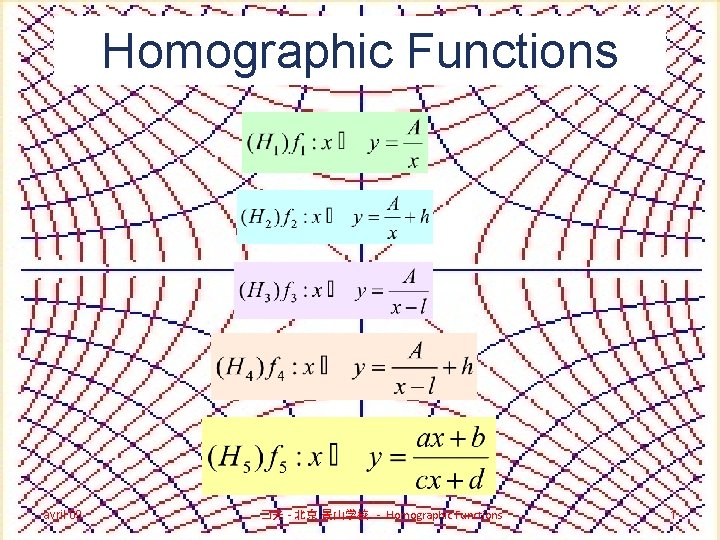
Homographic Functions avril 09 �光 - 北京 景山学校 - Homographic Functions 1

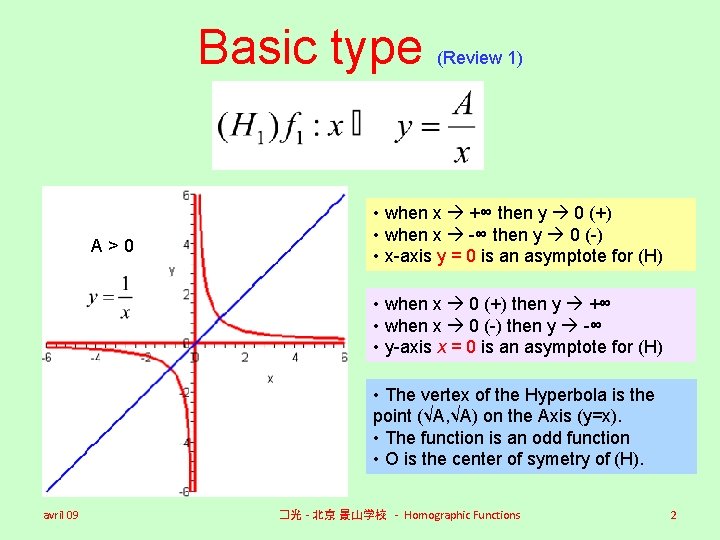
Basic type A>0 (Review 1) • when x +∞ then y 0 (+) • when x -∞ then y 0 (-) • x-axis y = 0 is an asymptote for (H) • when x 0 (+) then y +∞ • when x 0 (-) then y -∞ • y-axis x = 0 is an asymptote for (H) • The vertex of the Hyperbola is the point (√A, √A) on the Axis (y=x). • The function is an odd function • O is the center of symetry of (H). avril 09 �光 - 北京 景山学校 - Homographic Functions 2

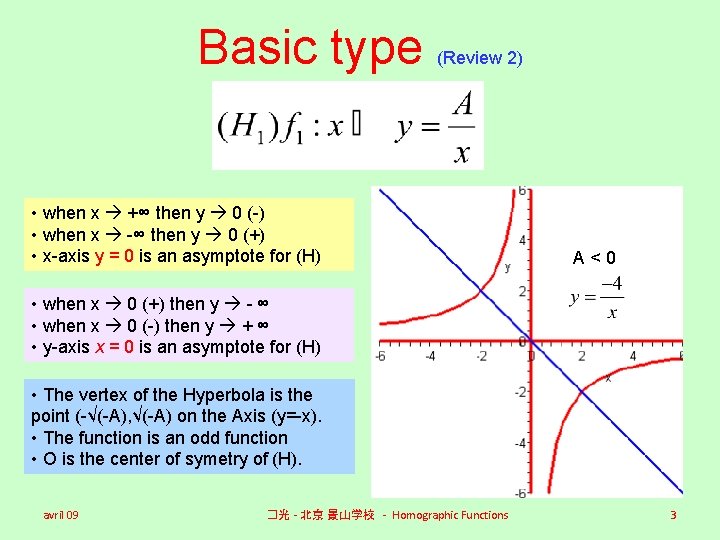
Basic type (Review 2) • when x +∞ then y 0 (-) • when x -∞ then y 0 (+) • x-axis y = 0 is an asymptote for (H) A<0 • when x 0 (+) then y - ∞ • when x 0 (-) then y + ∞ • y-axis x = 0 is an asymptote for (H) • The vertex of the Hyperbola is the point (-√(-A), √(-A) on the Axis (y=-x). • The function is an odd function • O is the center of symetry of (H). avril 09 �光 - 北京 景山学校 - Homographic Functions 3

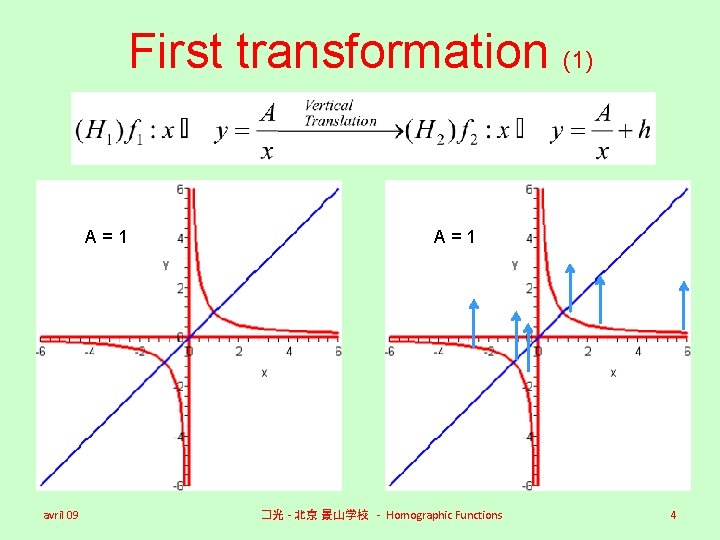
First transformation (1) A=1 avril 09 A=1 �光 - 北京 景山学校 - Homographic Functions 4

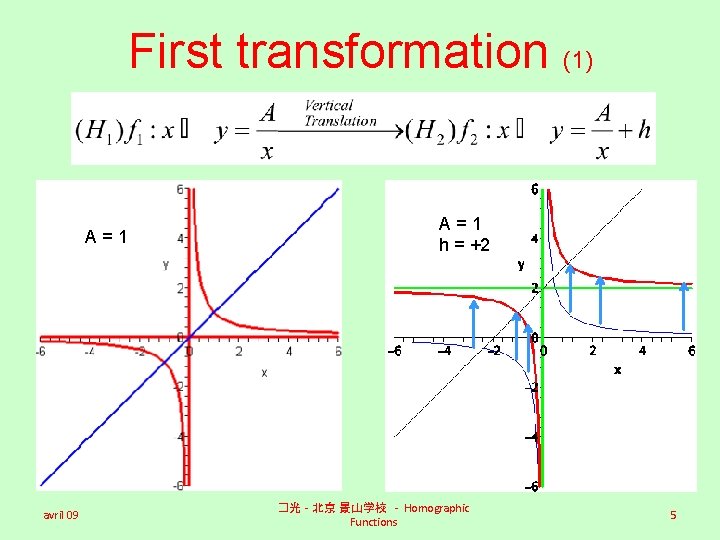
First transformation (1) A=1 avril 09 A=1 h = +2 �光 - 北京 景山学校 - Homographic Functions 5

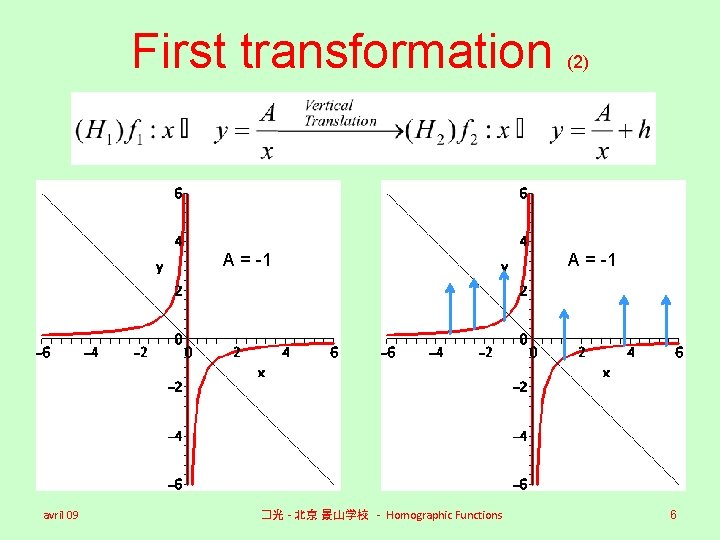
First transformation A = -1 avril 09 �光 - 北京 景山学校 - Homographic Functions (2) A = -1 6

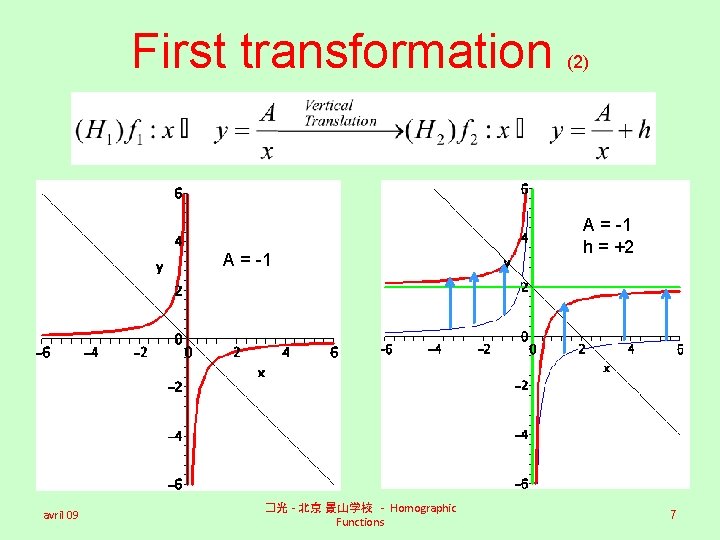
First transformation A = -1 avril 09 �光 - 北京 景山学校 - Homographic Functions (2) A = -1 h = +2 7

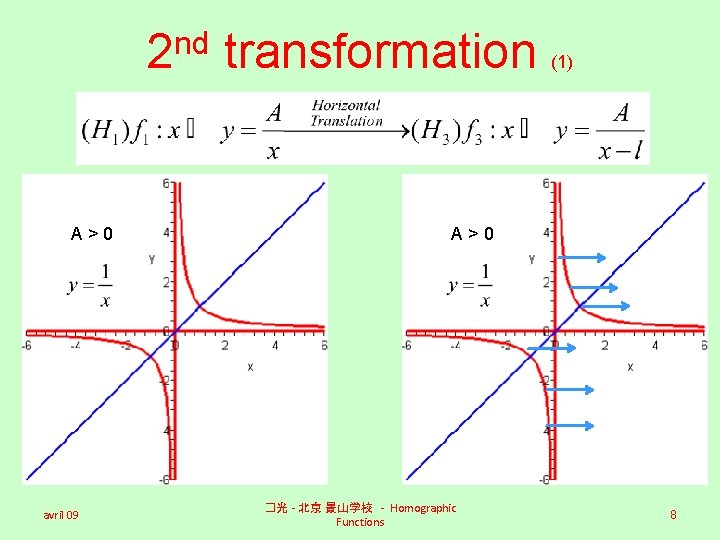
nd 2 A>0 avril 09 transformation (1) A>0 �光 - 北京 景山学校 - Homographic Functions 8

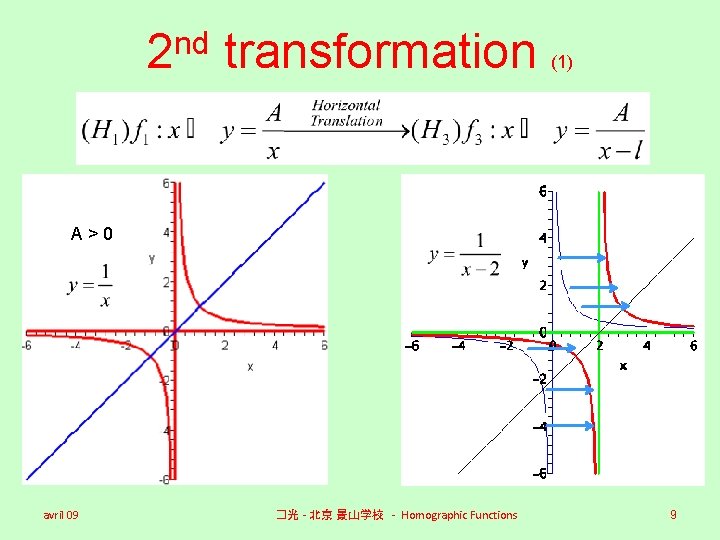
nd 2 transformation (1) A>0 avril 09 �光 - 北京 景山学校 - Homographic Functions 9

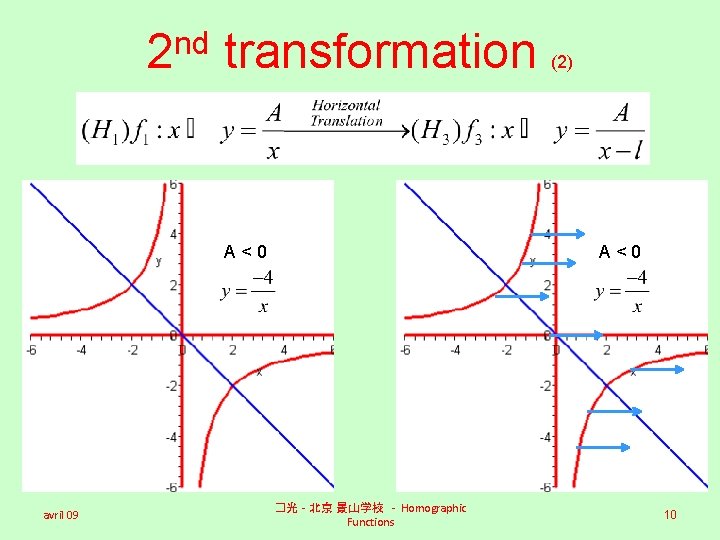
nd 2 transformation A<0 avril 09 (2) A<0 �光 - 北京 景山学校 - Homographic Functions 10

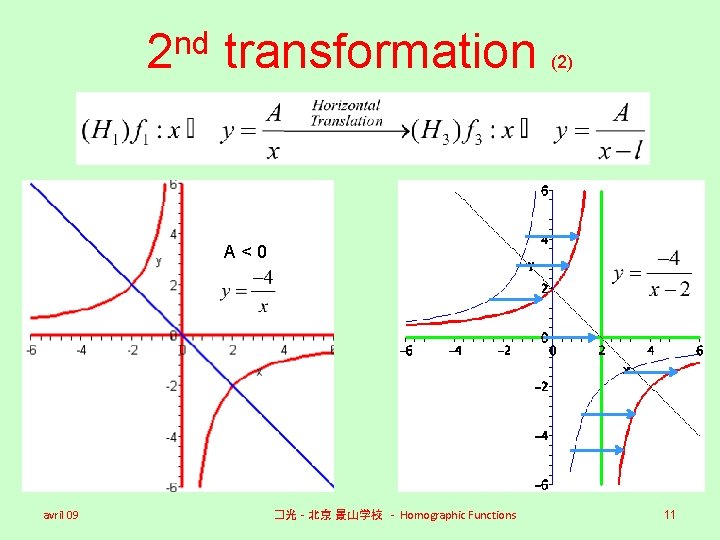
nd 2 transformation (2) A<0 avril 09 �光 - 北京 景山学校 - Homographic Functions 11

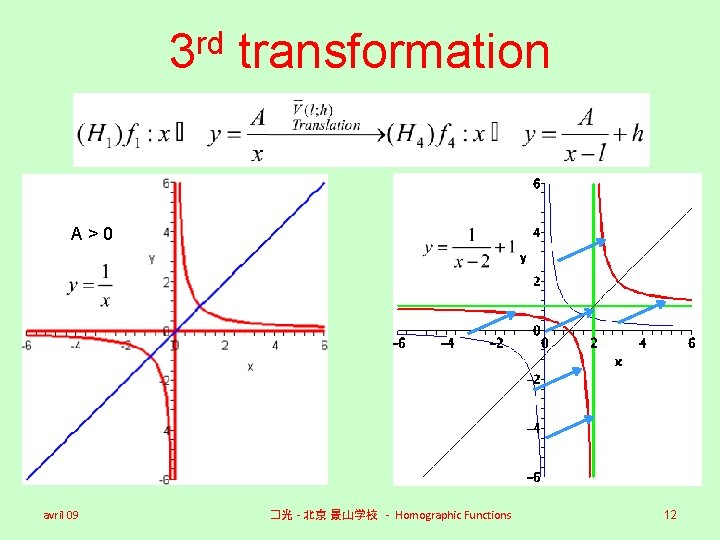
rd 3 transformation A>0 avril 09 �光 - 北京 景山学校 - Homographic Functions 12

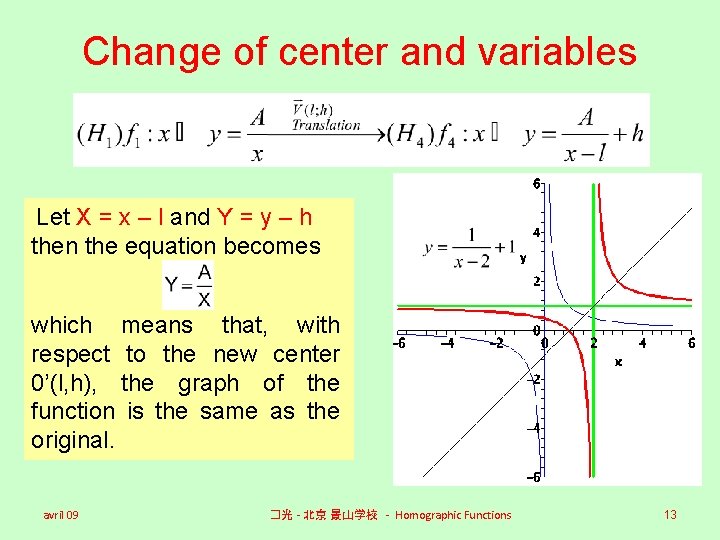
Change of center and variables Let X = x – l and Y = y – h then the equation becomes which means that, with respect to the new center 0’(l, h), the graph of the function is the same as the original. avril 09 �光 - 北京 景山学校 - Homographic Functions 13

Limits & Asymptotes • when x +∞ or x - ∞ then y h (±) the line y = h is an asymptote for (H) • when x l (±) then y ±∞ the line x = l is an asymptote for (H) • The point (l, h) intersection of the two asymptotes is the center of symmetry of the hyperbola. avril 09 �光 - 北京 景山学校 - Homographic Functions 14

General case • It’s easy to check that all functions in the type of can be changed into the form of f 5(x). Example : • Problem : prove that all functions defined by : can be transformed into the previous one. Example : avril 09 �光 - 北京 景山学校 - Homographic Functions 15

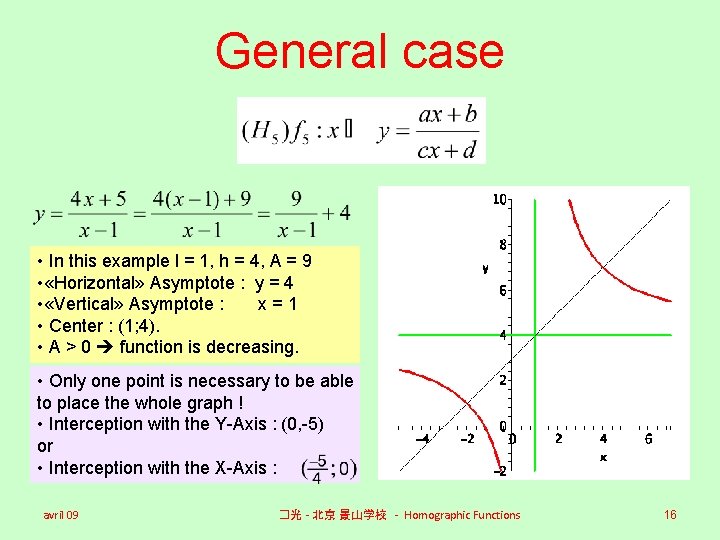
General case • In this example l = 1, h = 4, A = 9 • «Horizontal» Asymptote : y = 4 • «Vertical» Asymptote : x=1 • Center : (1; 4). • A > 0 function is decreasing. • Only one point is necessary to be able to place the whole graph ! • Interception with the Y-Axis : (0, -5) or • Interception with the X-Axis : avril 09 �光 - 北京 景山学校 - Homographic Functions 16

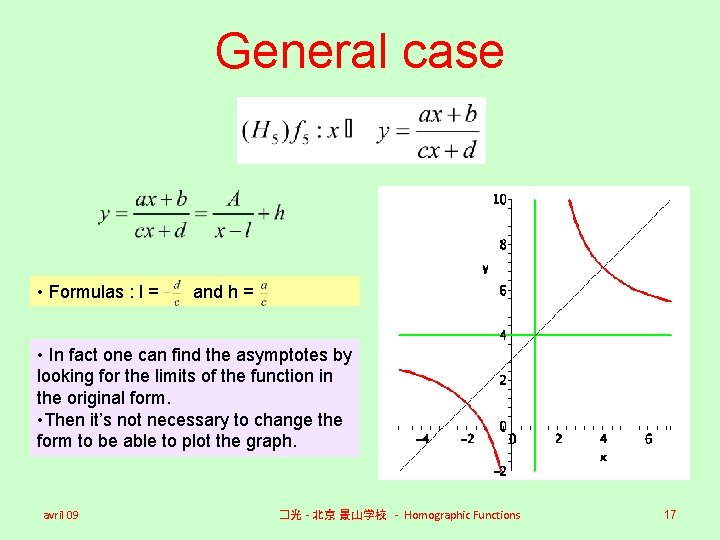
General case • Formulas : l = and h = • In fact one can find the asymptotes by looking for the limits of the function in the original form. • Then it’s not necessary to change the form to be able to plot the graph. avril 09 �光 - 北京 景山学校 - Homographic Functions 17

祝好运 谢谢 再见 avril 09 �光 - 北京 景山学校 - Homographic Functions 18