Homogeneous Transformation Matrices 3 x 3 Rotation Matrix

Homogeneous Transformation Matrices • 3 x 3 Rotation Matrix • 3 x 1 Displacement Vector • 4 x 4 Homogeneous Matrix January 24, 2000 Robotics 1 Copyright Martin P. Aalund, Ph. D. .

Homogeneous Transformation Matrices • What does a pure translation look like • What does a pure rotation look like • Multiply to move from one coordinate to another. January 24, 2000 Robotics 1 Copyright Martin P. Aalund, Ph. D. .

D-H Parameters • Denavit-Hartenberg (D-H) are used to describe a robot link. • One Coordinate System is created for each link. – Each Axes is orthogonal – Use the right hand rule • Link are assumed to be rigid • Four Parameters are used – – dn an qn an January 24, 2000 Distance Between Links Common Normal Distance Joint Angle Offset Angle Robotics 1 Copyright Martin P. Aalund, Ph. D. .

an • Common Normal Distance usually a positive value. • Is the distance from axes n to axes n+1 along the common perpendicular – – Common perpendicular is shortest distance between two lines in space. Does not necessarily lie in the physical link. If axes intersect then it is zero. Not defined for Prismatic, set to zero z 2 z 1 a 1 January 24, 2000 Robotics 1 Copyright Martin P. Aalund, Ph. D. .

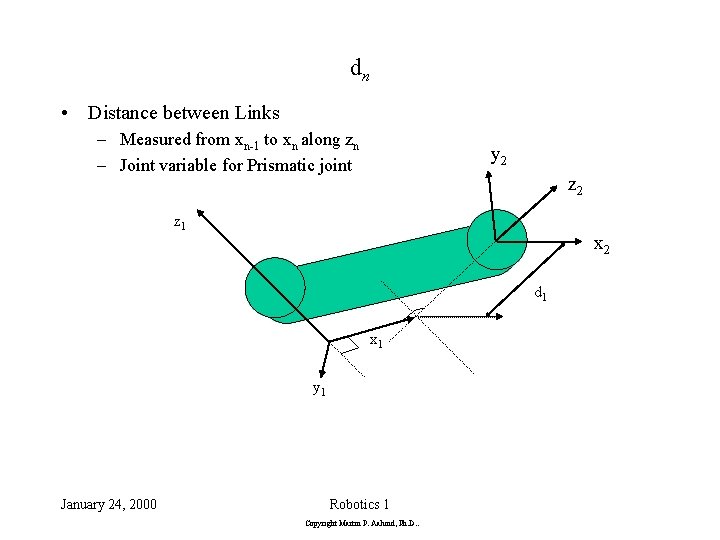
dn • Distance between Links – Measured from xn-1 to xn along zn – Joint variable for Prismatic joint y 2 z 1 x 2 d 1 x 1 y 1 January 24, 2000 Robotics 1 Copyright Martin P. Aalund, Ph. D. .

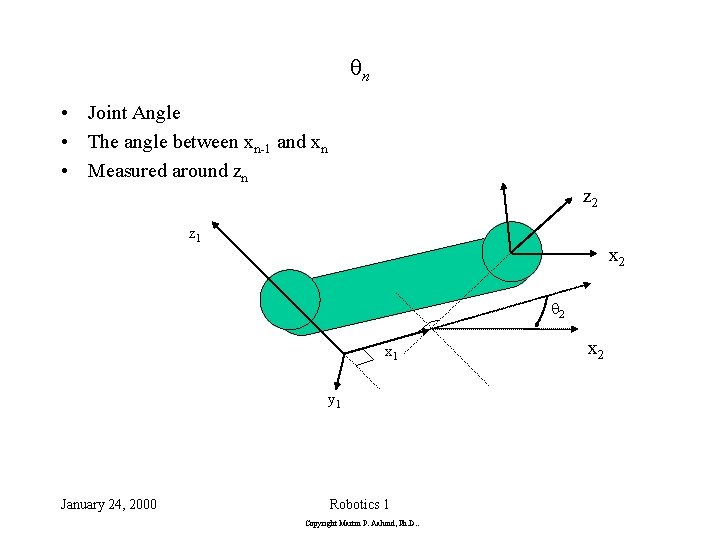
qn • Joint Angle • The angle between xn-1 and xn • Measured around zn z 2 z 1 x 2 q 2 x 1 y 1 January 24, 2000 Robotics 1 Copyright Martin P. Aalund, Ph. D. . x 2

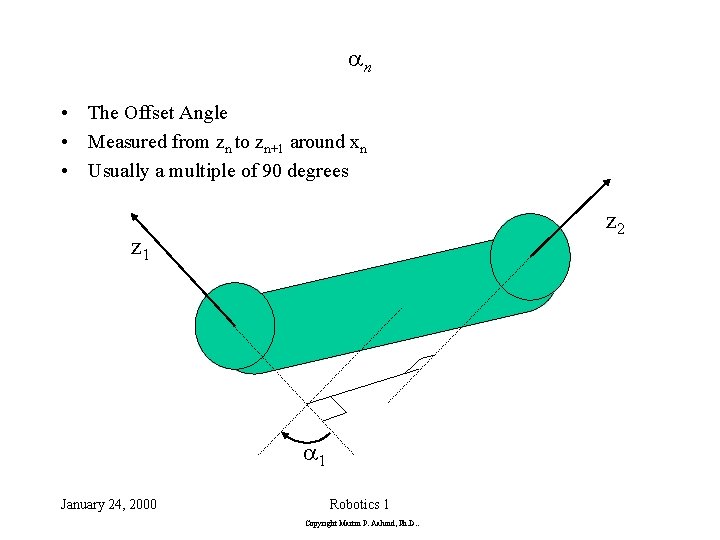
an • The Offset Angle • Measured from zn to zn+1 around xn • Usually a multiple of 90 degrees z 2 z 1 a 1 January 24, 2000 Robotics 1 Copyright Martin P. Aalund, Ph. D. .

Assigning Coordinate Frames • The base frame (0) is fixed and does not move. It is usually picked to be coincident with frame 1 • First place the Z axes along the joint axes of rotation, or translation. • Next place the X axes along the common perpendicular between axes n and n+1 • Use the right hand rule to define the Y axes. January 24, 2000 Robotics 1 Copyright Martin P. Aalund, Ph. D. .

Special Cases • If an=0 (the Z axes intersect) then pick Xn to be normal to the plane defined by Zn and Zn-1. This leads to two possible Definitions of X and thus Y. • If Zn and Zn+1 are parallel then dn is 0 January 24, 2000 Robotics 1 Copyright Martin P. Aalund, Ph. D. .

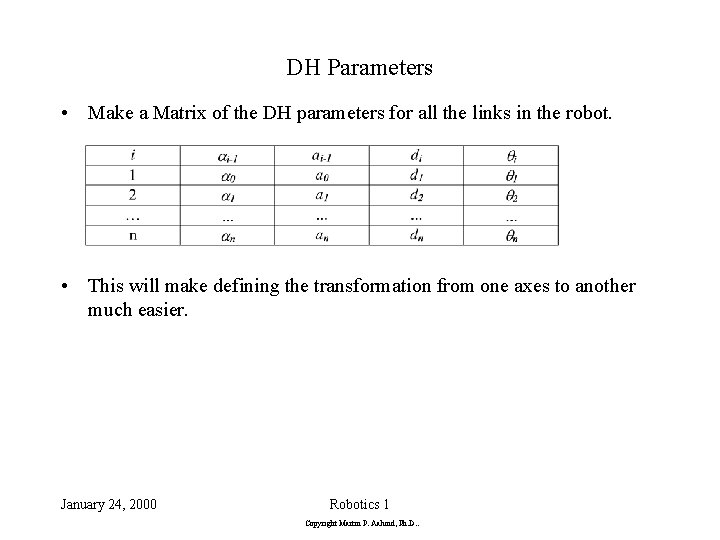
DH Parameters • Make a Matrix of the DH parameters for all the links in the robot. • This will make defining the transformation from one axes to another much easier. January 24, 2000 Robotics 1 Copyright Martin P. Aalund, Ph. D. .

DH Based Transformation Matrices January 24, 2000 Robotics 1 Copyright Martin P. Aalund, Ph. D. .

Forward Kinematics • Used to mover from Joint coordinates to end-effector coordinates • Just Multiply the individual T matrices. • For a robot with N joints we will get N Transformations • If we are interested in a point beyond the last joint such as an endeffector or tool. We define a coordinate system for the Tool point of interest and create a transform from the last joint to the point. • We will find it helpful to define other points in the robot work space with coordinate systems relative to the robot base system. January 24, 2000 Robotics 1 Copyright Martin P. Aalund, Ph. D. .

Standard Frames include • Wrist Frame {W} Same as the last robot frame I. e. Frame {N} • Base frame {B} Located at the base of the manipulator same as frame {0} • Station frame {S} Usually used as the base point for robot motions. Calculated relative to the Base Frame • Tool Frame {T} Could be tip of a torch, point between finger of a gripper or the lens of a camera. specified relative to the {W} Frame • Goal Frame {G} Location where the robot is desired to move. At the end of motion the {G} and {T} should coincide. • So to get from the Station frame to the toll frame we simply calculate: Where January 24, 2000 Robotics 1 Copyright Martin P. Aalund, Ph. D. .