Homogeneous representation n Points n Vectors n Transformation

Homogeneous representation n Points n Vectors n Transformation n representation Stefano Soatto (c) UCLA Vision Lab 1

Lecture 4: Image formation Stefano Soatto (c) UCLA Vision Lab 2

Image Formation n Vision infers world properties form images. How do images depend on these properties? Two key elements q q q Geometry Radiometry We consider only simple models of these Stefano Soatto (c) UCLA Vision Lab 3

Image formation (Chapter 3) Stefano Soatto (c) UCLA Vision Lab 4

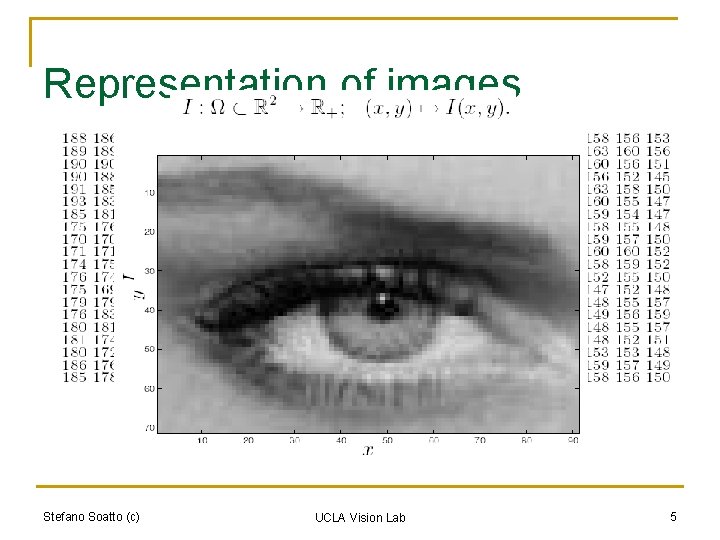
Representation of images Stefano Soatto (c) UCLA Vision Lab 5

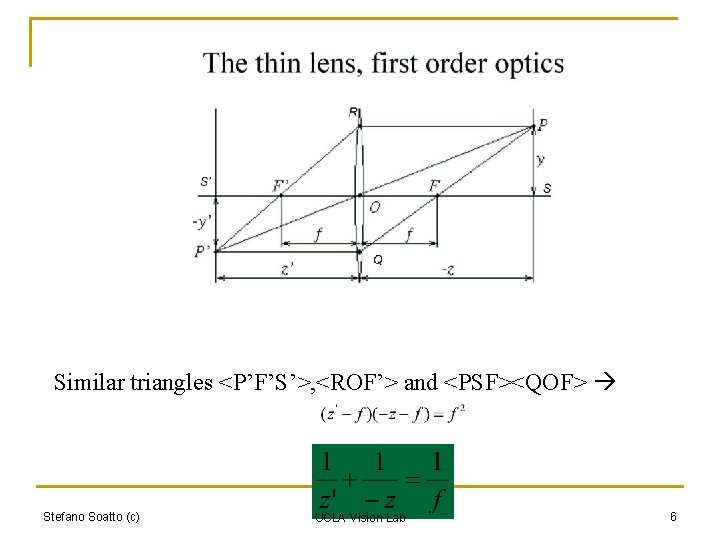
Similar triangles <P’F’S’>, <ROF’> and <PSF><QOF> Stefano Soatto (c) UCLA Vision Lab 6

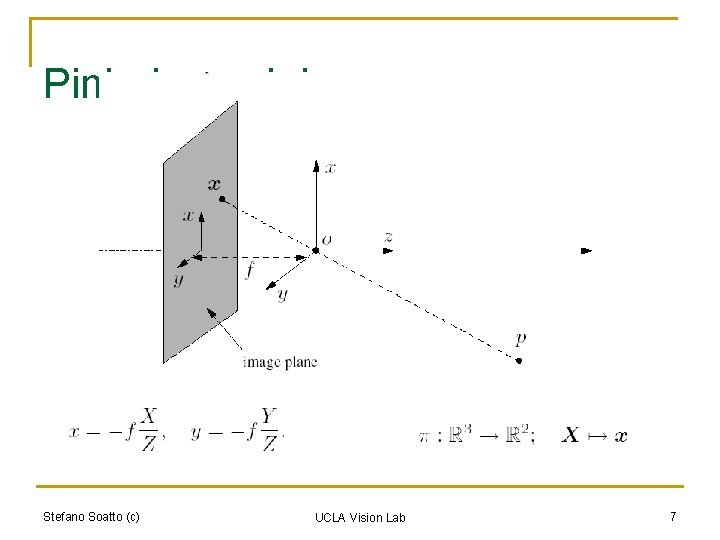
Pinhole model Stefano Soatto (c) UCLA Vision Lab 7

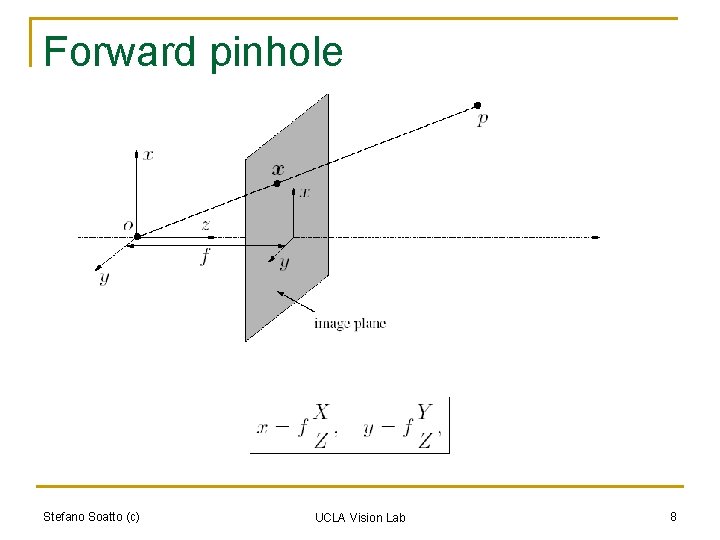
Forward pinhole Stefano Soatto (c) UCLA Vision Lab 8

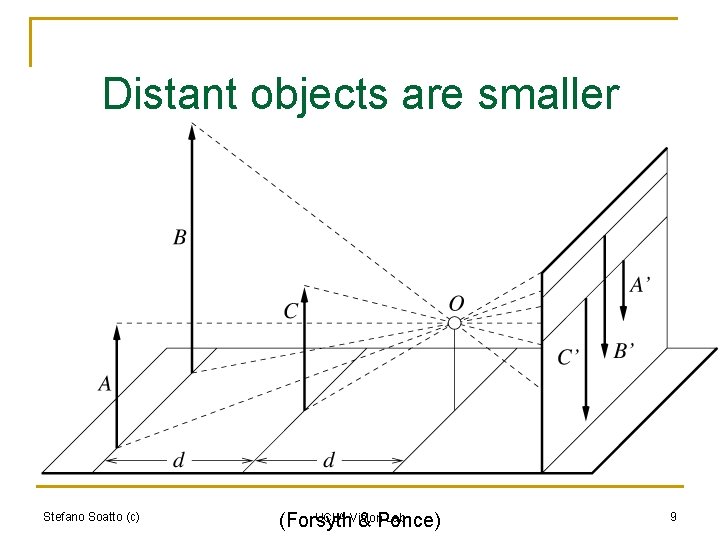
Distant objects are smaller Stefano Soatto (c) UCLA Vision Lab (Forsyth & Ponce) 9

Parallel lines meet Common to draw image plane in front of the focal point. Moving the image plane merely scales the image. Stefano Soatto (c) UCLA Vision Lab (Forsyth & Ponce) 10

Vanishing points • Each set of parallel lines meets at a different point – The vanishing point for this direction • Sets of parallel lines on the same plane lead to collinear vanishing points. – The line is called the horizon for that plane Stefano Soatto (c) UCLA Vision Lab 11

Properties of Projection n n Points project to points Lines project to lines Planes project to the whole image or a half image Angles are not preserved Degenerate cases q q q Line through focal point projects to a point. Plane through focal point projects to line Plane perpendicular to image plane projects to part of the image (with horizon). Stefano Soatto (c) UCLA Vision Lab 12

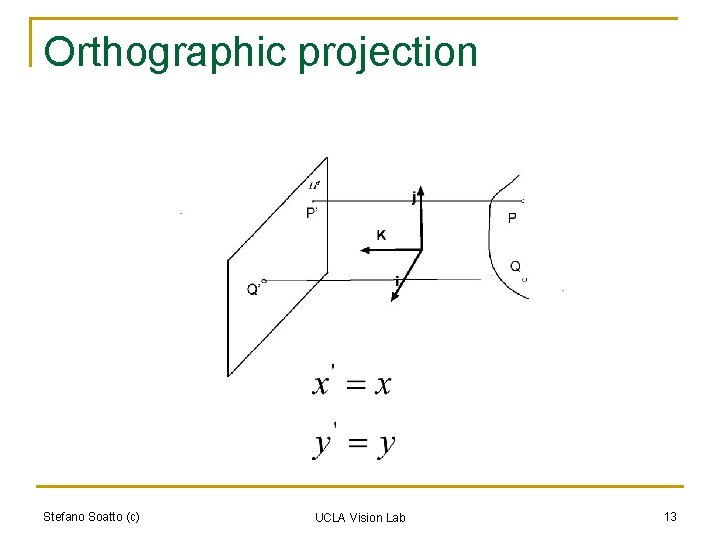
Orthographic projection Stefano Soatto (c) UCLA Vision Lab 13

Stefano Soatto (c) UCLA Vision Lab 14

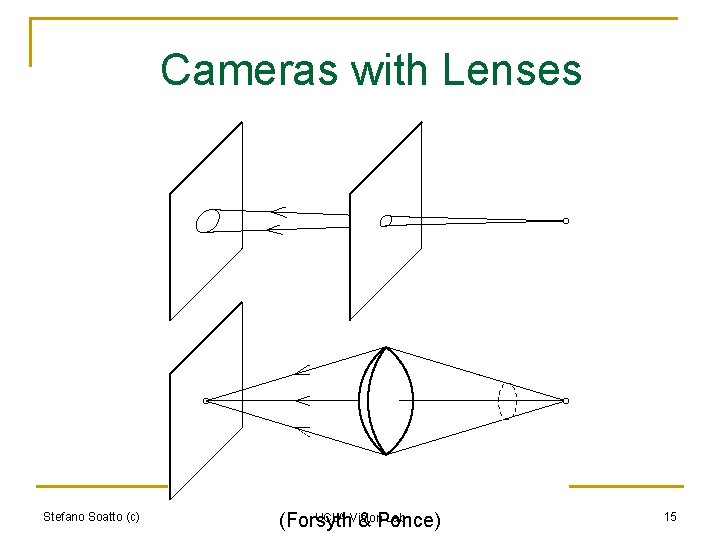
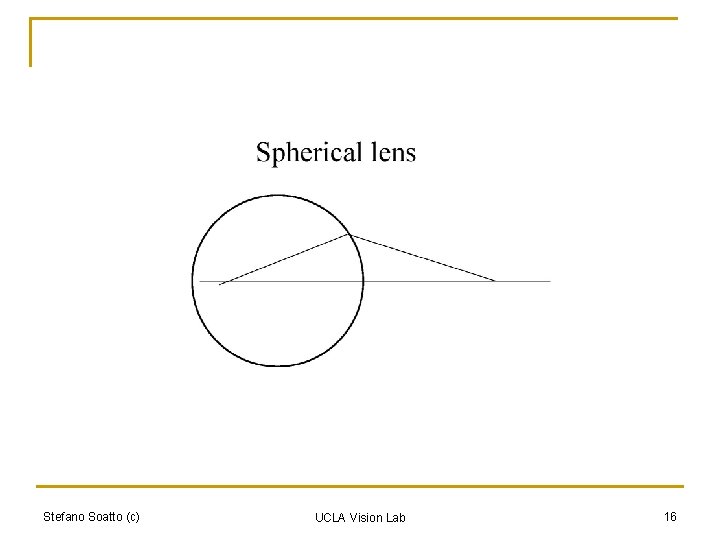
Cameras with Lenses Stefano Soatto (c) UCLA Vision Lab (Forsyth & Ponce) 15

Stefano Soatto (c) UCLA Vision Lab 16

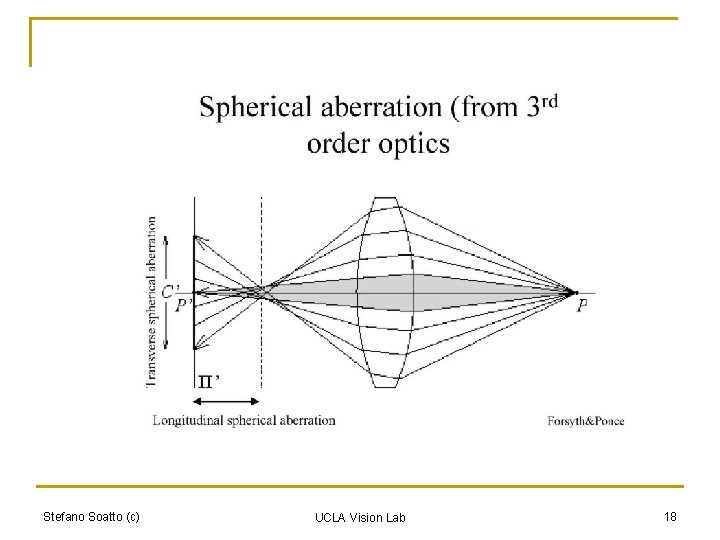
Assumptions for thin lens equation n n Lens surfaces are spherical Incoming light rays make a small angle with the optical axis The lens thickness is small compared to the radii of curvature The refractive index is the same for the media on both sides of the lens Stefano Soatto (c) UCLA Vision Lab 17

Stefano Soatto (c) UCLA Vision Lab 18

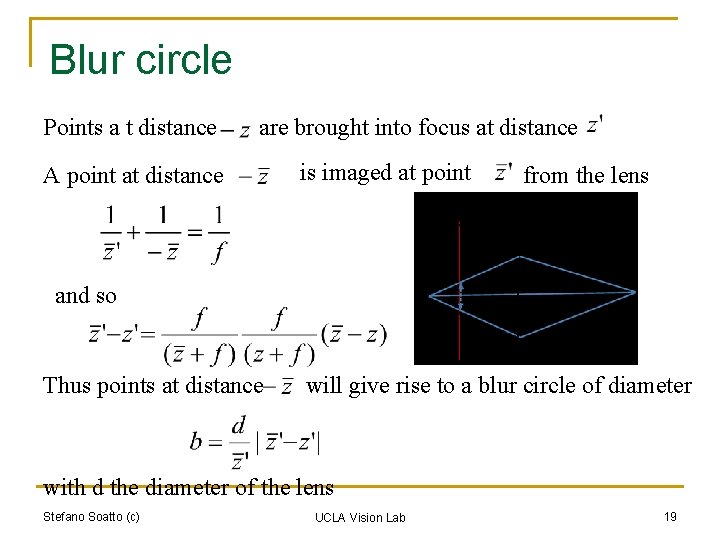
Blur circle Points a t distance are brought into focus at distance A point at distance is imaged at point from the lens and so Thus points at distance will give rise to a blur circle of diameter with d the diameter of the lens Stefano Soatto (c) UCLA Vision Lab 19

Interaction of light with matter n n n Absorption Scattering Refraction Reflection Other effects: q q Diffraction: deviation of straight propagation in the presence of obstacles Fluorescence: absorbtion of light of a given wavelength by a fluorescent molecule causes reemission at another wavelength Stefano Soatto (c) UCLA Vision Lab 20

Refraction n 1, n 2: indexes of refraction Stefano Soatto (c) UCLA Vision Lab 21

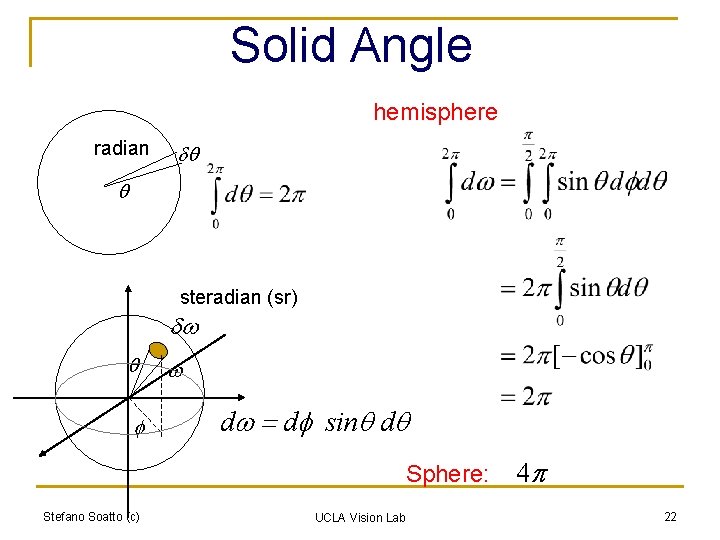
Solid Angle hemisphere radian dq q steradian (sr) dw q f w dw = df sinq dq Sphere: Stefano Soatto (c) UCLA Vision Lab 4 p 22

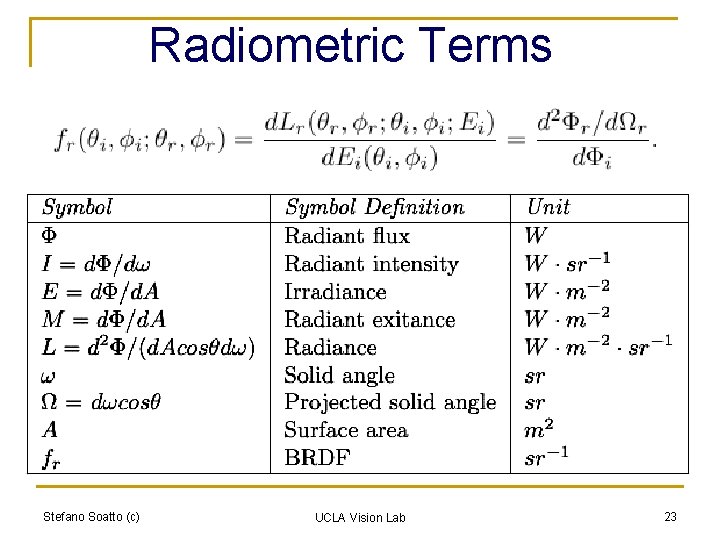
Radiometric Terms Stefano Soatto (c) UCLA Vision Lab 23

Irradiance and Radiance Irradiance Definition: power per unit area incident on a surface [W/m 2 = lux] Radiance Definition: power per unit area and projected solid angle [W/m 2 sr] Stefano Soatto (c) UCLA Vision Lab 24

Radiant Intensity Definition: flux per unit solid angle [W/sr = cd (candela)] : Radiant flux [W] [ ] Stefano Soatto (c) UCLA Vision Lab 25

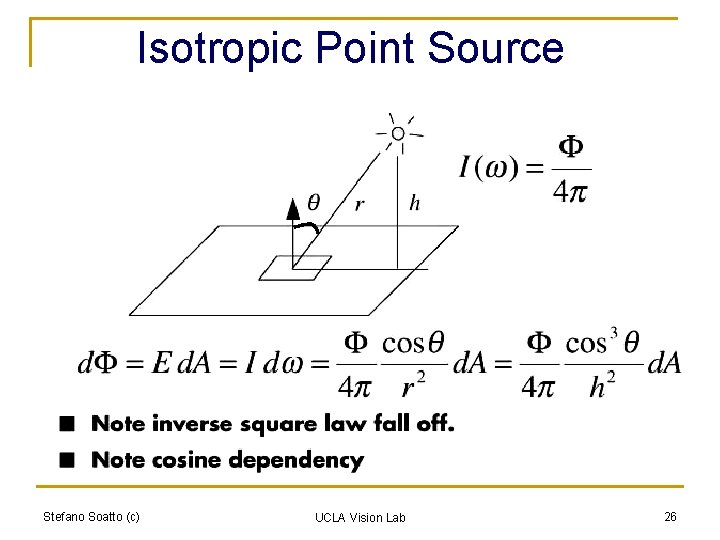
Isotropic Point Source Stefano Soatto (c) UCLA Vision Lab 26

Isotropic Point Source : Radiant flux [W] All directions: solid angle 4 p : Radiant flux per unit solid angle [W/sr] r : Radiant intensity • Note inverse square law fall off. Stefano Soatto (c) UCLA Vision Lab 27

Isotropic Point Source : Radiant flux [W] All directions: solid angle r Stefano Soatto (c) 4 p : Radiant flux per unit solid angle [W/sr] : Radiant intensity h • Note cosine dependency. UCLA Vision Lab 28

Isotropic Point Source Point source at a finite distance r h • Note inverse square law fall off. • Note cosine dependency. Stefano Soatto (c) UCLA Vision Lab 29

Irradiance from Area Sources Stefano Soatto (c) UCLA Vision Lab 30

Hemispherical Source L Stefano Soatto (c) UCLA Vision Lab 31

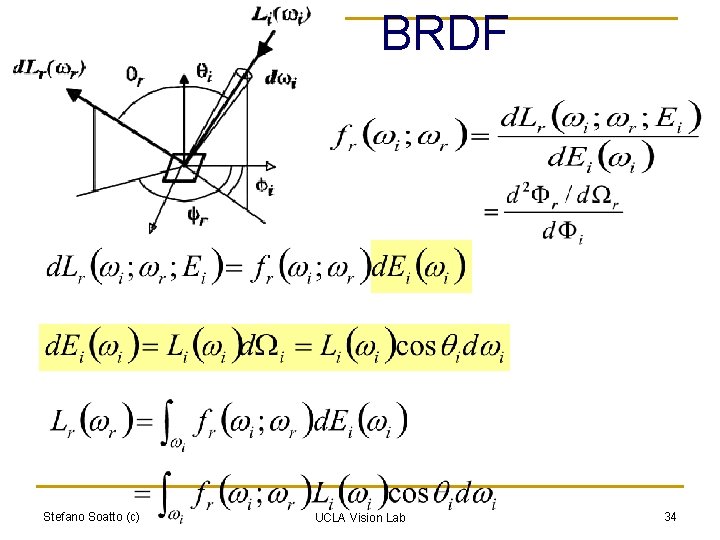
Reflectance Li(x, wi) The surface becomes a light source Lr(x, w) qi Ei Ei d. Lr=fr d. Ei Reflectance: ratio of radiance to irradiance Stefano Soatto (c) UCLA Vision Lab 32

BRDF Stefano Soatto (c) UCLA Vision Lab 33

BRDF Stefano Soatto (c) UCLA Vision Lab 34

Reflection Equation Stefano Soatto (c) UCLA Vision Lab 35

qi Perfectly Diffuse Reflection Perfectly Diffuse Surface • Appears equally bright from all viewing directions (qr, fr) • Reflects all incident light, i. e. , LB(qr, fr) is constant for all directions (qr, fr) Stefano Soatto (c) UCLA Vision Lab 36

qi Common Diffuse Reflection Normal Diffuse Surface • Appears almost equally bright from most viewing directions (qr, fr), qr << 90° • Reflects only a fraction of incident light, i. e. , Reflectance : Albedo Stefano Soatto (c) UCLA Vision Lab 37

Perfectly Diffuse Reflection Distant point light source qi Lambertian cosine Law Stefano Soatto (c) UCLA Vision Lab 38

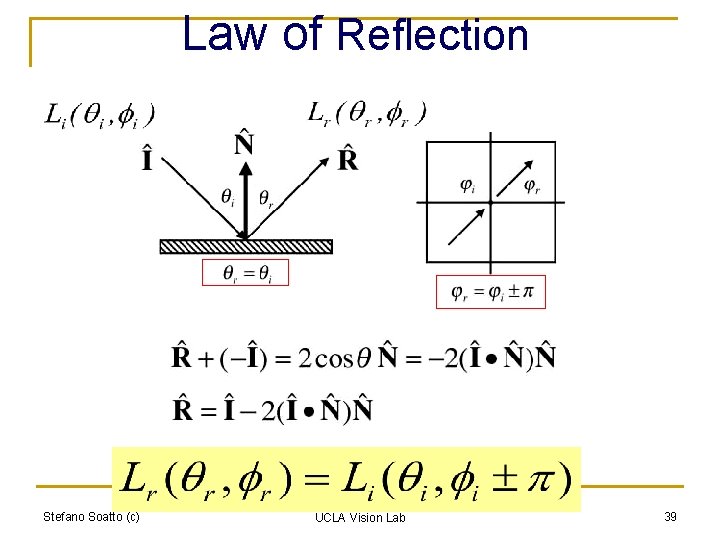
Law of Reflection Stefano Soatto (c) UCLA Vision Lab 39

Perfectly Specular Reflection From the definition of BRDF, the surface radiance is: To satisfy: Stefano Soatto (c) UCLA Vision Lab 40

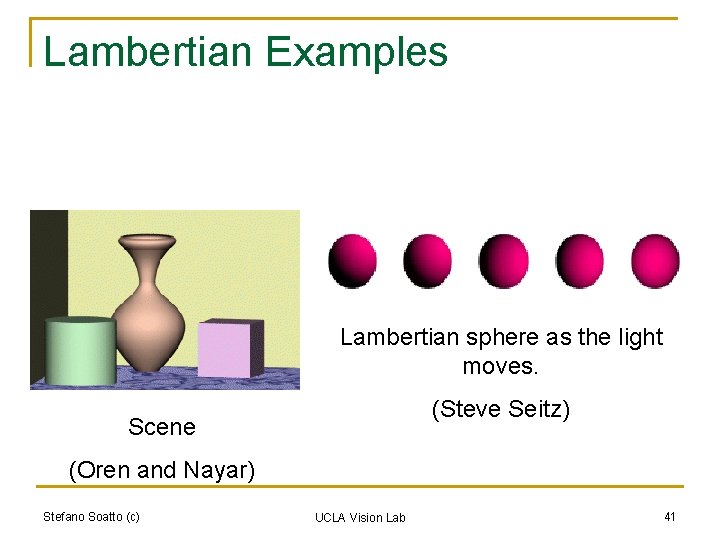
Lambertian Examples Lambertian sphere as the light moves. (Steve Seitz) Scene (Oren and Nayar) Stefano Soatto (c) UCLA Vision Lab 41

Lambertian + Specular Model Stefano Soatto (c) UCLA Vision Lab 42

Lambertian + specular • Two parameters: how shiny, what kind of shiny. • Advantages – easy to manipulate – very often quite close true • Disadvantages – some surfaces are not • e. g. underside of CD’s, feathers of many birds, blue spots on many marine crustaceans and fish, most rough surfaces, oil films (skin!), wet surfaces – Generally, very little advantage in modelling behaviour of light at a surface in more detail -- it is quite difficult to understand behaviour of L+S surfaces (but in graphics? ? ? ) Stefano Soatto (c) 43 UCLA Vision Lab

Lambertian+Specular+Ambient (http: //graphics. ucdavis. edu/Graphics. Notes/Shading. html) Stefano Soatto (c) UCLA Vision Lab 44