Homogeneous Coordinates and Transformation 1 Line in General





![Definitions Points on P 2: I. [(u, v, w)] with w 0 Choose a Definitions Points on P 2: I. [(u, v, w)] with w 0 Choose a](https://slidetodoc.com/presentation_image_h2/7a9b5ba7de6b9233b28d0c58cd2dc49c/image-8.jpg)

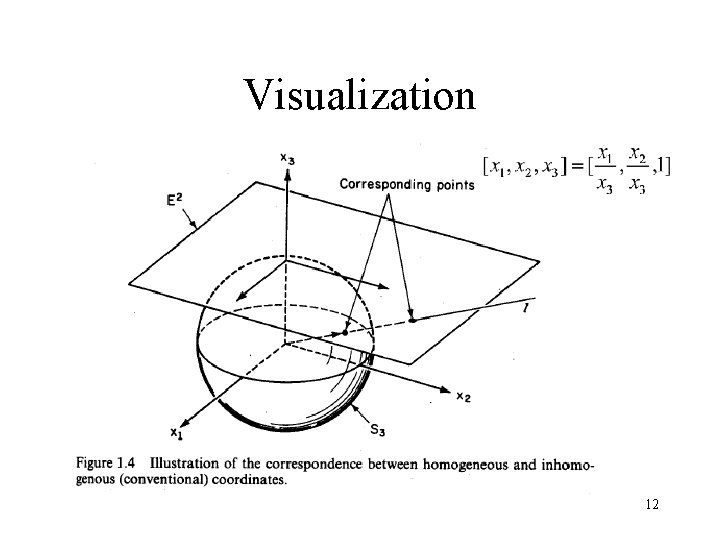
![Visualization • Line model [and spherical model] 11 Visualization • Line model [and spherical model] 11](https://slidetodoc.com/presentation_image_h2/7a9b5ba7de6b9233b28d0c58cd2dc49c/image-11.jpg)











- Slides: 30

Homogeneous Coordinates and Transformation 1

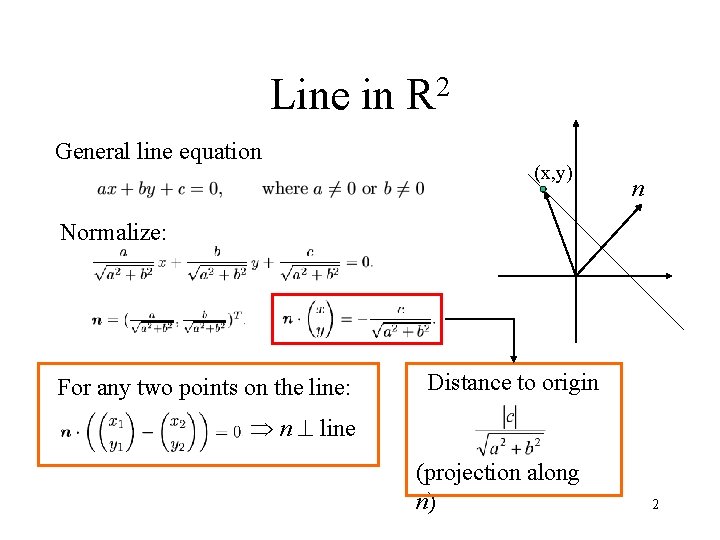
Line in General line equation 2 R (x, y) n Normalize: For any two points on the line: Distance to origin n line (projection along n) 2

Line in 2 R Parametric equation of a line Corresponding implicit form: Implicitize: 3

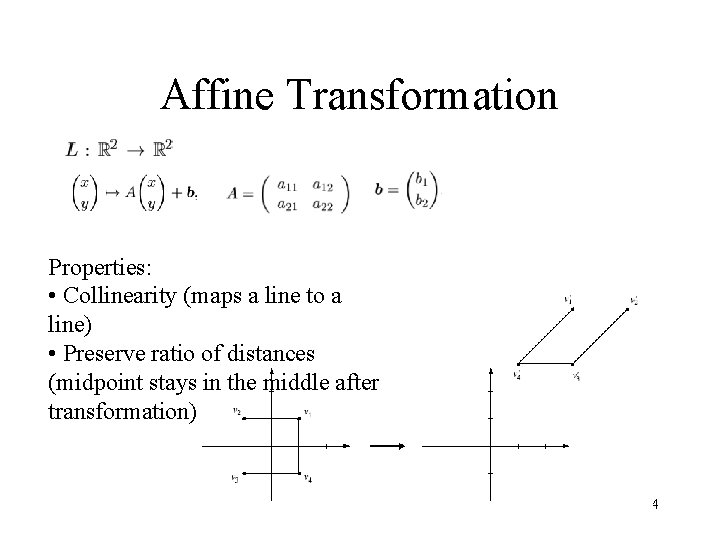
Affine Transformation Properties: • Collinearity (maps a line to a line) • Preserve ratio of distances (midpoint stays in the middle after transformation) 4

Common 2 D Affine Transformations • • • Translation Scaling Reflection (Q = I– 2 uu. T) Rotation about origin Shear 5

Homogeneous Coordinate • Motivation: to unify representations of affine map (esp. translation) 6

Definitions Equivalence relation ~ on the set S = R 3 {(0, 0, 0)} Ex: Show that this relation is reflexive, symmetric, and transitive Equivalence classes of the relation ~ Homogeneous coordinates Projective plane P 2: the set of all equivalence classes An equivalence class is referred to as a point in the projective plane. 7
![Definitions Points on P 2 I u v w with w 0 Choose a Definitions Points on P 2: I. [(u, v, w)] with w 0 Choose a](https://slidetodoc.com/presentation_image_h2/7a9b5ba7de6b9233b28d0c58cd2dc49c/image-8.jpg)
Definitions Points on P 2: I. [(u, v, w)] with w 0 Choose a representative (u/w, v/w, 1) 1 -1 correspondence with Cartesian plane II. [(u, v, w)] with w = 0 Corresponds to points-at-infinity, each with a specific direction Points on P 2: the plane R 2 plus all the points at infinity 8

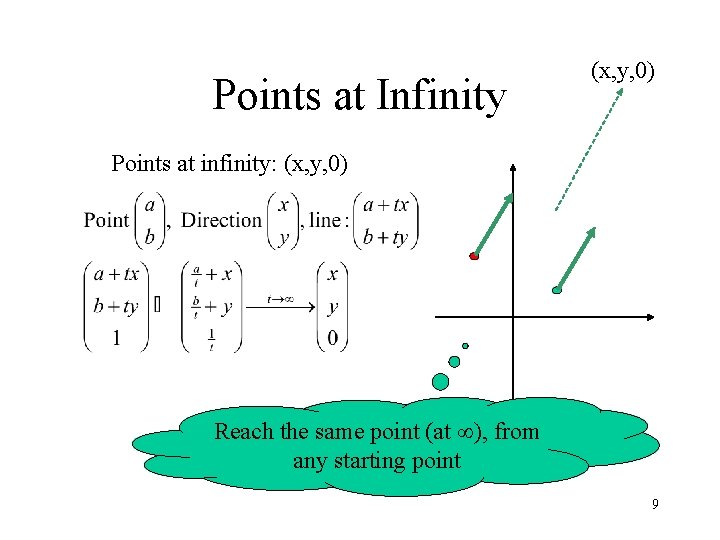
Points at Infinity (x, y, 0) Points at infinity: (x, y, 0) Reach the same point (at ), from any starting point 9

Parallel Lines Intersect at Infinity (-2, 1, 0) 10
![Visualization Line model and spherical model 11 Visualization • Line model [and spherical model] 11](https://slidetodoc.com/presentation_image_h2/7a9b5ba7de6b9233b28d0c58cd2dc49c/image-11.jpg)
Visualization • Line model [and spherical model] 11

Visualization 12

Line in Cartesian Space (or any multiple of it) 13

Examples (cases in R 2) • The line passes through (3, 1) and (4, 5) • Intersection of 14

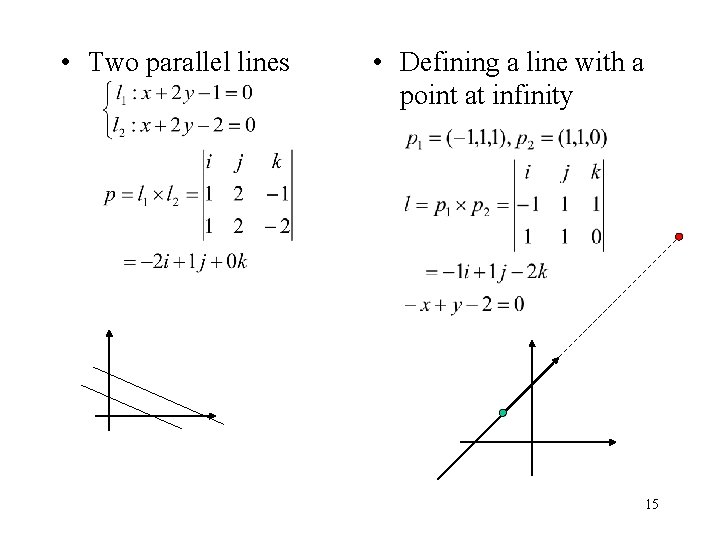
• Two parallel lines • Defining a line with a point at infinity 15

Extend to P 3 and R 3 Plane in Cartesian Space 16

Intersection of Three Planes 17

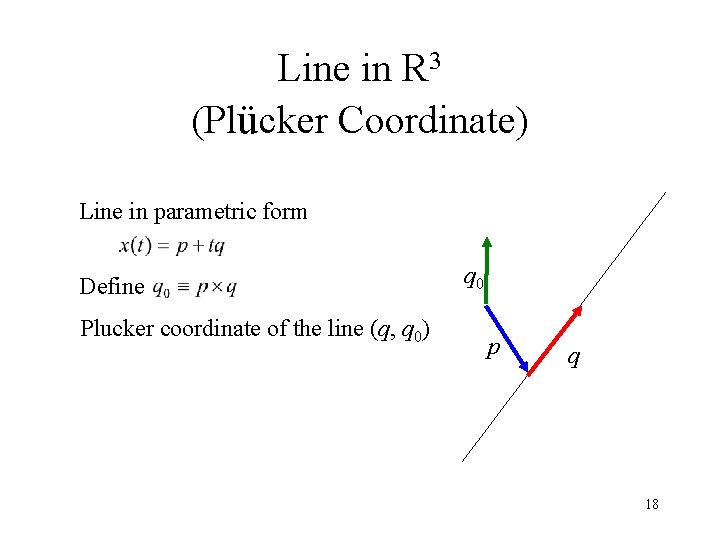
Line in R 3 (Plücker Coordinate) Line in parametric form Define Plucker coordinate of the line (q, q 0) q 0 p q 18

Space Transformation • • • Translation Scaling Rotation about coordinate axes Rotation about arbitrary line Reflection about arbitrary plane (Q=I– 2 uu. T) 19

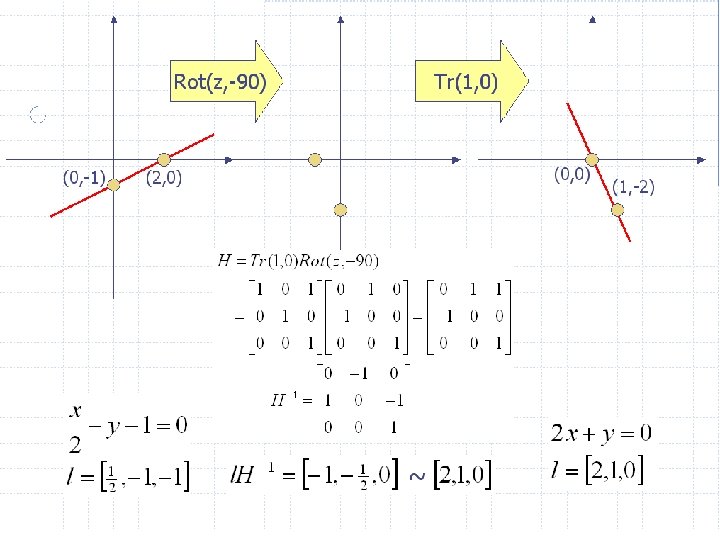
Transformed Equations If transformation T is applied to geometry (line/plane), what’s the transformed equation? • Apply T to homogenous line/plane equation? ! NOT !! Answers: • See handout p. 3 (convert to parametric form; transform the points; then to implicit equation) • More detailed version: see “homogeneoustransformation. ppt” from R. Paul (next page) • Also related to the normal matrix in Open. GL. 20

From Richard Paul Ch. 1 21

Summary Point u on a plane: After transformation H Point u becomes v = Hu Plane P’ becomes PH-1 Reason: Note if P is written as a column vector, the formula becomes P’ = H-TP 22

23

Transformed Quadrics Point u on a quadric: After transformation H Reason: Point u becomes v = Hu Quadric Q becomes H-TQH-1 24

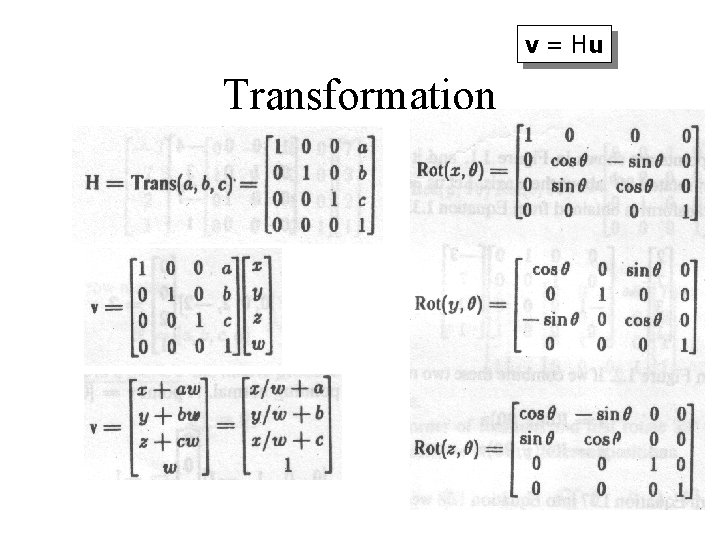
v = Hu Transformation 25

From Opengl-1. ppt 26

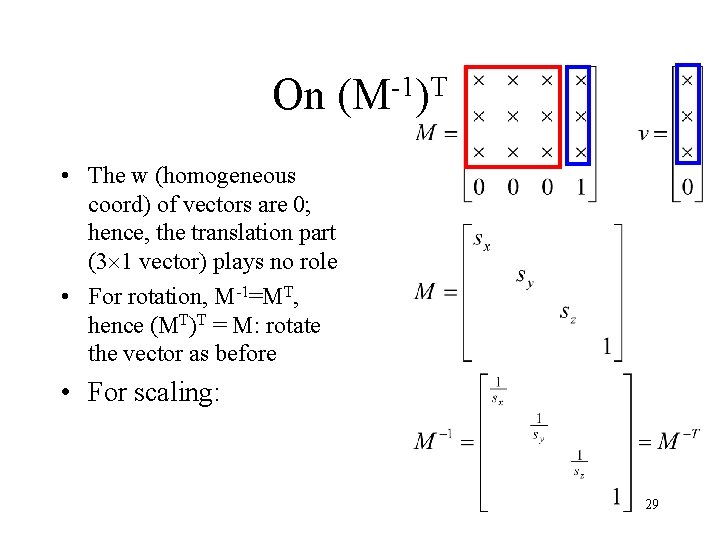
Vectors and Points are Different! gl. Vertex Point • Homogenenous coordinate p = [x y z 1] • M: affine transform (translate, rotate, scaling, reflect, …) p’= M p gl. Normal Vector • Homogeneous coordinate v = [x y z 0] • Affine transform (applicable when M is invertible (not full rank; projection to 2 D is not) v’= (M-1)T v (ref) 27

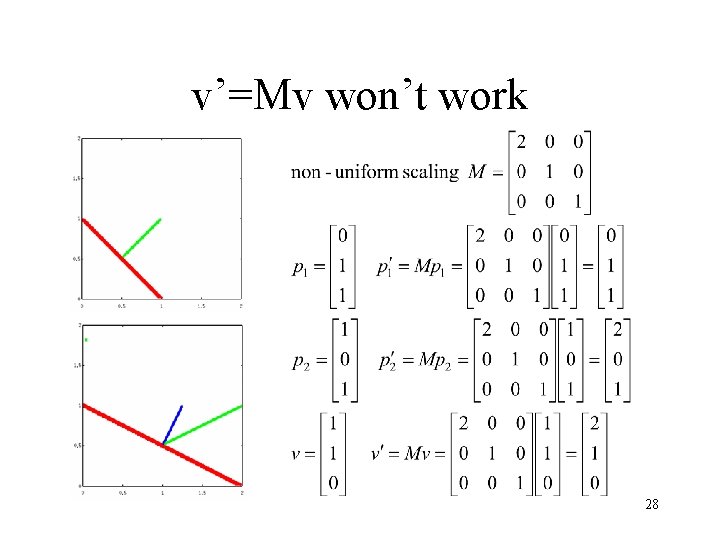
v’=Mv won’t work 28

On -1 T (M ) • The w (homogeneous coord) of vectors are 0; hence, the translation part (3 1 vector) plays no role • For rotation, M-1=MT, hence (MT)T = M: rotate the vector as before • For scaling: 29

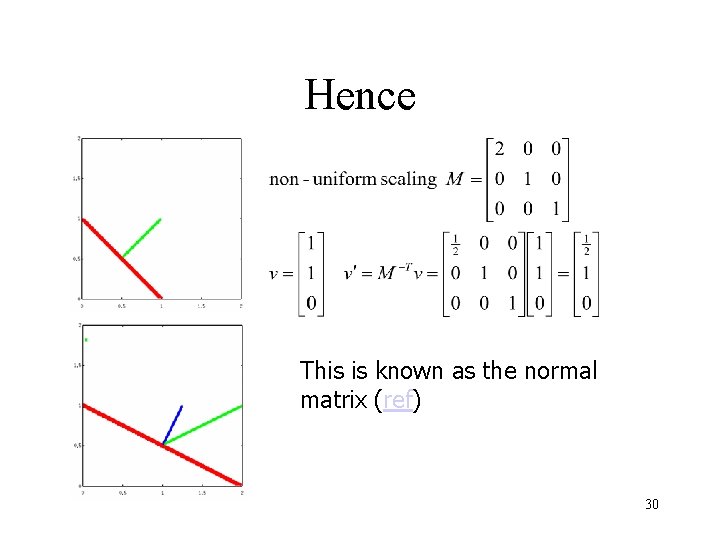
Hence This is known as the normal matrix (ref) 30