Homework Review Probability The Counting Principle Finding Sets

Homework Review

Probability The Counting Principle & Finding Sets

Use an appropriate method to find the number of outcomes in each of the following situations: 1. Your school cafeteria offers chicken or tuna sandwiches; chips or fruit; and milk, apple juice, or orange juice. If you purchase one sandwich, one side item and one drink, how many different lunches can you choose? There are 12 possible lunches. Sandwich(2) Side Item(2) chips chicken fruit chips tuna fruit Drink(3) Outcomes apple juice orange juice milk chicken, chips, apple chicken, chips, orange chicken, chips, milk chicken, fruit, apple chicken, fruit, orange chicken, fruit, milk apple juice orange juice milk tuna, chips, apple tuna, chips, orange tuna, chips, milk tuna, fruit, apple tuna, fruit, orange tuna, fruit, milk

Easier Way No need to make the tree diagram. Multiply each of the number of choices (2 sandwiches, 2 sides, 3 drinks)

Counting Principle • At a sporting goods store, skateboards are available in 8 different deck designs. Each deck design is available with 4 different wheel assemblies. How many skateboard choices does the store offer? 32

Counting Principle • A father takes his son, Marcus, to Wendy’s for lunch. He tells Marcus he can get a 5 piece nuggets, a spicy chicken sandwich, or a single for the main entrée. For sides, he can get fries, a side salad, potato, or chili. And for drinks, he can get a frosty, coke, sprite, or an orange drink. How many options for meals does Marcus have? 48

I-Pods can vary the order in which songs are played. Your I-Pod currently only contains 8 songs. Find the number of orders in which the songs can be played. There are 40, 320 possible song orders. 1 st Song 2 nd 3 rd 4 th 5 th 6 th 7 th 8 th Outcomes In this situation it makes more sense to use the Fundamental Counting Principle. 8 • 7 • 6 • 5 • 4 • 3 • 2 • 1 = 40, 320 The solutions in examples 3 and 4 involve the product of all the integers from n to one. The product of all positive integers less than or equal to a number is a factorial.

The Price is Right The Race Game One Away

Practice

SET NOTATION

Probability A number from 0 to 1 As a percent from 0% to 100% Indicates how likely an event will occur

Diagram from Walch Education

Experiment Any process or action that has observable results. Example: drawing a card from a deck of cards is an experiment

Outcomes Results from experiments Example: all the cards in the deck are possible outcomes

Sample Space The set (or list) of all possible outcomes. Also known as the universal set Example: listing out all the cards in the deck would be the sample space

Event A subset of an experiment An outcome or set of desired outcomes Example: drawing a single Jack of hearts

Set List or collection of items

Subset List or collection of items all contained within another set Denoted by A B, if all the elements of A are also in B.

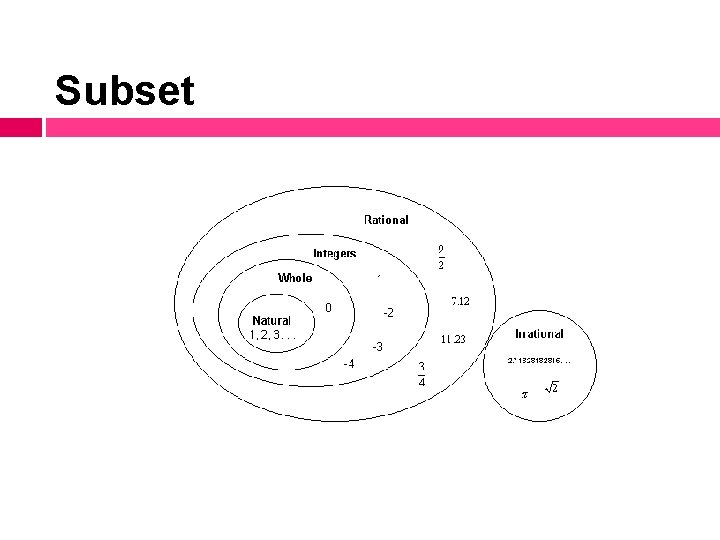
Subset

Example Let A be all multiples of 4 and B be all multiples of 2. • A = {. . . , -8, -4, 0, 4, 8, . . . } • B = {. . . , -8, -6, -4, -2, 0, 2, 4, 6, 8, . . . } Is A a subset of B? And is B a subset of A?

Empty Set A set that has NO elements Also called a null set. Denoted by As an example, think of the set of piano keys on a guitar.