Homework Polynomial Long Division 2 3 Polynomial Division






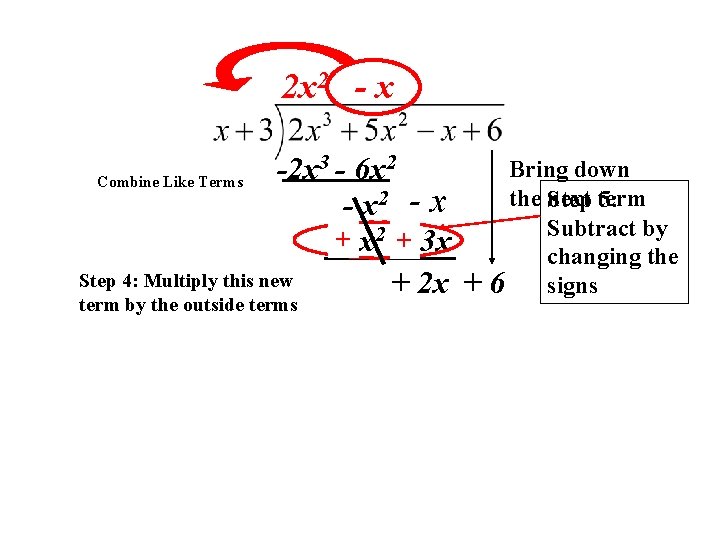





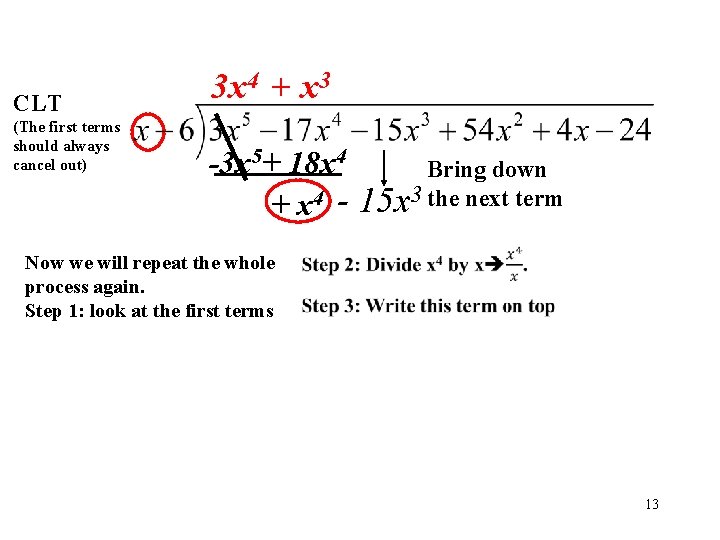








- Slides: 21

Homework: Polynomial Long Division

2. 3 Polynomial Division Objective: • Divide polynomials using long division 2

Polynomial Long Division Divide : (2 x 3 + 5 x 2 - x + 6) (x + 3) Step 1: Write the problem using a division symbol Step 2: Look at the first term on the outside and the inside

2 x 2 ? Put 2 x 2 on the top So, the term we are looking for is 2 x 2

2 x 2 Multiply the term you just wrote on top by the outside terms. - 2 x 3 + 6 x 2 2 x 2(x + 3) = 2 x 3 + 6 x 2 (This answer will be written in the next line, under the correct powers) The next step is subtraction so we have: -(2 x 3 + 6 x 2) = -2 x 3 - 6 x 2 Be sure to subtract by changing the signs of every term.

Combine Like Terms (The first terms should always cancel out) Now we will repeat the whole process again. Step 1: look at the first term 2 x 2 - x -2 x 3 - 6 x 2 - x Bring down the next term
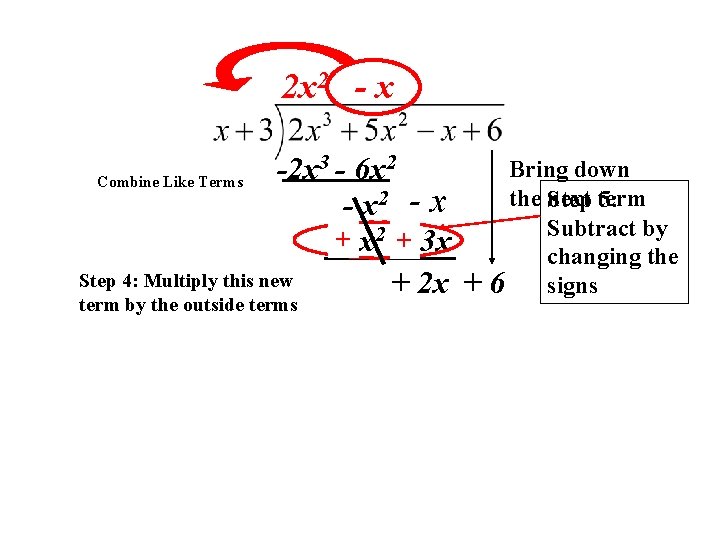
2 x 2 - x 3 - 6 x 2 Bring down -2 x Combine Like Terms the Step next term 5: - x 2 - x Subtract by +- x 2 +- 3 x changing the Step 4: Multiply this new + 2 x + 6 signs term by the outside terms

ANSWER IS ON TOP Repeat Steps 1 -5 Step 1: Look at first terms Step 2: Divide first term 2 x by x? Step 3: Write result above the line Step 4: Multiply new term by outside terms Step 5: Subtract by changing the signs! 2 x 2 - x + 2 -2 x 3 - 6 x 2 - x 2 + 3 x + x CLT (The first terms + 2 x + 6 should always cancel out) +- 2 x +- 6 0 Subtract by changing the signs of every term.

Polynomial Long Division Divide : (3 x 5 - 17 x 4 - 15 x 3 + 4 x + 54 x 2 – 24) by (x – 6) PROBLEM: Terms out of descending order SOLUTION: Rearrange terms into descending order

Polynomial Long Division Divide : (3 x 5 - 17 x 4 - 15 x 3 + 54 x 2 + 4 x – 24) (x – 6) Step 1: Write the problem using a division symbol Step 2: Look at the first term on the outside and the inside 10

3 x ? 4 Put 3 x 4 on the top So, the term we are looking for is 3 x 4 11

Multiply the term you just wrote on top by the outside terms. 3 x 4(x - 6) = 3 x 5 - 18 x 4 3 x 4 - 3 x 5 +- 18 x 4 The next step is subtraction so we have: -(3 x 5 - 18 x 4) = -3 x 5+ Be sure to change the signs of every term. 18 x 4 12
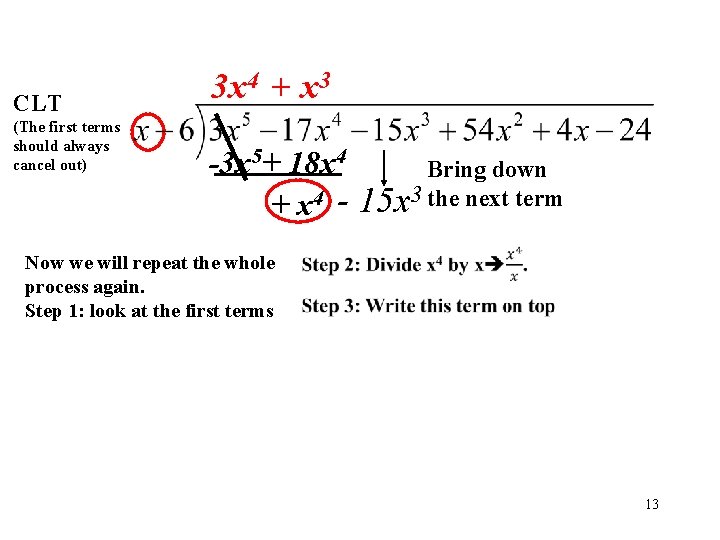
CLT (The first terms should always cancel out) 3 x 4 + x 3 -3 x 5+ 18 x 4 Bring down + x 4 - 15 x 3 the next term Now we will repeat the whole process again. Step 1: look at the first terms 13

3 x 4 + x 3 5+ 18 x 4 Bring down -3 x CLT sure to + x 4 - 15 x 3 the next. Beterm (The first terms should always change the 4 3 +- x -+ 6 x cancel out) signs of Step 4: Multiply this new - 9 x 3 + 54 x 2 every term by the outside terms Step 5: Subtract by changing the signs. 14

Repeat Steps 1 -5 Step 1: Look at first terms 3 x 4 + x 3 - 9 x 2 5+ 18 x 4 -3 x Bring down Step 2: Divide? + x 4 - 15 x 3 the next term Step 3: Write this above the line 4 + 6 x 3 x CLT Step 4: Multiply (The first terms 3 + 54 x 2 9 x new term by should always 3 - 54 x 2 cancel out) outside terms +- 9 x + Step 5: Subtract by 2 + 4 x 0 x changing signs and CLT Subtract by changing the signs of every term. 15

Repeat Steps 1 -5 Step 1: Look at first terms Step 2: Divide? Step 3: Write this above the line Step 4: Multiply new term by outside terms Step 5: Subtract by changing signs and CLT 3 x 4 + x 3 - 9 x 2 + 0 x -3 x 5+ 18 x 4 Bring down + x 4 - 15 x 3 the next term - x 4 + 6 x 3 - 9 x 3 + 54 x 2 + 9 x 3 - 54 x 2 CLT 2 + 4 x (The first terms + 0 x always Be should sure to cancel out) - 0 x 2 +- 0 x + change the + 4 x - 24 signs of every term. 16

ANSWER IS ON TOP Repeat Steps 1 -5 Step 1: Look at first terms Step 2: Divide? Step 3: Write this above the line Step 4: Multiply new term by outside terms Step 5: Subtract by changing the signs and CLT 3 x 4 + x 3 - 9 x 2 + 0 x + 4 -3 x 5+ 18 x 4 + x 4 - 15 x 3 - x 4 + 6 x 3 - 9 x 3 + 54 x 2 - 9 x 3 - 54 x 2 + 0 x 2 + 4 x CLT - 0 x 2 + 0 x (The first terms + 4 x - 24 should Be sure to always cancel out) +- 4 x +- 24 change the signs of every term. 0 17

The division problems we just worked ended with zero remainders. Now let’s work a problem that ends with a remainder that’s not a zero. 18

Example: Divide Using Long Division (2 x 4 + 4 x 3 – 5 x 2 + 3 x – 2) (x 2 + 2 x – 3) 19

Example: Divide Using Long Division (x 4– 10 x 2 – 2 x + 4) (x + 3) 20

Sneedlegrit: Divide Using Long Division (x 3 + 4 x 2 – 3 x – 12) (x 2 – 3) Homework: Polynomial Long Division 21