Homework Part I Write the prime factorization of

Homework: Part I Write the prime factorization of each number. 1. 50 2. 84 Find the GCF of each pair of numbers. 3. 18 and 75 4. 20 and 36

Homework: Part II Find the GCF each pair of monomials. 5. 12 x and 28 x 3 6. 27 x 2 and 45 x 3 y 2 7. Cindi is planting a rectangular flower bed with 40 orange flowers and 28 yellow flowers. She wants to plant them so that each row will have the same number of plants but of only one color. How many rows will Cindi need if she puts the greatest possible number of plants in each row?

Warm Up Tell whether the second number is a factor of the first number. 1. 50, 6 no 2. 105, 7 yes 3. List the factors of 28. ± 1, ± 2, ± 4, ± 7, ± 14, ± 28 Tell whether each number is prime or composite. If the number is composite, write it as the product of two numbers. 4. 11 prime 5. 98 composite; 49 2

Vocabulary prime factorization greatest common factor

The numbers that are multiplied to find a product are called factors of that product. A number is divisible by its factors. Remember that a prime number is a whole number that has exactly two positive factors, itself and 1. The number 1 is not prime because it has only one factor. You can use the factors of a number to write the number as a product. The number 12 can be factored several ways.

Factorizations of 12 The order of factors does not change the product, but there is only one example that cannot be factored further. The circled factorization is the prime factorization because all the factors are prime numbers. The prime factors can be written in any order, and except for changes in the order, there is only one way to write the prime factorization of a number.

Additional Example 1: Writing Prime Factorizations Write the prime factorization of 98. Method 1 Factor tree Method 2 Ladder diagram Choose any two factors Choose a prime factor of 98 to begin. Keep finding to begin. Keep dividing by factors until each branch prime factors until the ends in a prime factor. quotient is 1. 98 2 98 7 49 2 49 7 7 7 7 1 98 = 2 7 7 The prime factorization of 98 is 2 7 7 or 2 72.

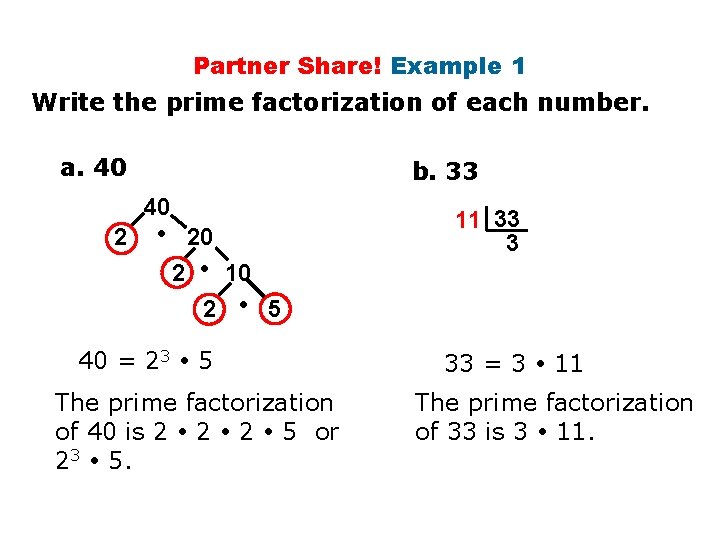
Partner Share! Example 1 Write the prime factorization of each number. a. 40 40 2 20 2 10 2 5 40 = 23 5 The prime factorization of 40 is 2 2 2 5 or 23 5. b. 33 11 33 3 33 = 3 11 The prime factorization of 33 is 3 11.

Partner Share! Example 1 Write the prime factorization of each number. c. 49 d. 19 49 7 7 49 = 7 7 The prime factorization of 49 is 7 7 or 72. 1 19 19 19 = 1 19 The prime factorization of 19 is 1 19.

Factors that are shared by two or more whole numbers are called common factors. The greatest of these common factors is called the greatest common factor, or GCF. Factors of 12: 1, 2, 3, 4, 6, 12 Factors of 32: 1, 2, 4, 8, 16, 32 Common factors: 1, 2, 4 The greatest of the common factors is 4.

Additional Example 2 A: Finding the GCF of Numbers Find the GCF of the pair of numbers. 100 and 60 Method 1 List the factors of 100: 1, 2, 4, 5, 10, 25, 50, 100 List all the factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 Circle the GCF. The GCF of 100 and 60 is 20.

Additional Example 2 B: Finding the GCF of Numbers Find the GCF of the pair of numbers. 26 and 52 Method 2 Prime factorization. 26 = 2 13 52 = 2 2 13 = 26 Write the prime factorization of each number. Align the common factors. The GCF of 26 and 52 is 26.

Partner Share! Example 2 a Find the GCF of the pair of numbers. 12 and 16 Method 1 List the factors of 12: 1, 2, 3, 4, 6, 12 List all the factors of 16: 1, 2, 4, 8, 16 Circle the GCF. The GCF of 12 and 16 is 4.

Partner Share! Example 2 b Find the GCF of the pair of numbers. 15 and 25 Method 2 Prime factorization. 15 = 3 5 25 = 5 5 5 The GCF of 15 and 25 is 5. Write the prime factorization of each number. Align the common factors.

You can also find the GCF of monomials that include variables. To find the GCF of monomials, write the prime factorization of each coefficient and write all powers of variables as products. Then find the product of the common factors.

Additional Example 3 A: Finding the GCF of Monomials Find the GCF of each pair of monomials. 15 x 3 and 9 x 2 15 x 3 = 3 5 x x x 9 x 2 = 3 3 x x 3 Write the prime factorization of each coefficient and write powers as products. Align the common factors. x x = 3 x 2 Find the product of the common factors. The GCF of 15 x 3 and 9 x 2 is 3 x 2.

Additional Example 3 B: Finding the GCF of Monomials Find the GCF of each pair of monomials. 8 x 2 and 7 y 3 Write the prime factorization of each 8 x 2 = 2 2 2 x x coefficient and write 7 y 3 = 7 y y y powers as products. Align the common factors. The GCF 8 x 2 and 7 y 3 is 1. There are no common factors other than 1.

Helpful Hint If two terms contain the same variable raised to different powers, the GCF will contain that variable raised to the lower power.

Partner Share! Example 3 a Find the GCF of each pair of monomials. 18 g 2 and 27 g 3 18 g 2 = 2 3 3 27 g 3 = g g Write the prime factorization of each coefficient and write powers as products. 3 3 3 g g g Align the common factors. 3 3 g g Find the product of the common factors. The GCF of 18 g 2 and 27 g 3 is 9 g 2.

Partner Share! Example 3 b Find the GCF of each pair of monomials. 16 a 6 and 9 b 16 a 6 = 2 2 a a a 9 b = The GCF of 16 a 6 and 9 b is 1. Write the prime factorization of each coefficient and write powers as products. 3 3 b Align the common factors. There are no common factors other than 1.

Partner Share! Example 3 c Find the GCF of each pair of monomials. 8 x and 7 v 2 8 x = 2 2 2 x 7 v 2 = Write the prime factorization of each coefficient and write powers as products. 7 v v Align the common factors. The GCF of 8 x and 7 v 2 is 1. There are no common factors other than 1.

Additional Example 4: Application A cafeteria has 18 chocolate-milk cartons and 24 regular-milk cartons. The cook wants to arrange the cartons with the same number of cartons in each row. Chocolate and regular milk will not be in the same row. How many rows will there be if the cook puts the greatest possible number of cartons in each row? The 18 chocolate and 24 regular milk cartons must be divided into groups of equal size. The number of cartons in each row must be a common factor of 18 and 24.

Additional Example 4 Continued Factors of 18: 1, 2, 3, 6, 9, 18 Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24 Find the common factors of 18 and 24. The GCF of 18 and 24 is 6. The greatest possible number of milk cartons in each row is 6. Find the number of rows of each type of milk when the cook puts the greatest number of cartons in each row.

Additional Example 4 Continued 18 chocolate milk cartons = 3 rows 6 containers per row 24 regular milk cartons 6 containers per row = 4 rows When the greatest possible number of types of milk is in each row, there are 7 rows in total.

Partner Share! Example 4 Adrianne is shopping for a CD storage unit. She has 36 CDs by pop music artists and 48 CDs by country music artists. She wants to put the same number of CDs on each shelf without putting pop music and country music CDs on the same shelf. If Adrianne puts the greatest possible number of CDs on each shelf, how many shelves does her storage unit need? The 36 pop and 48 country CDs must be divided into groups of equal size. The number of CDs in each row must be a common factor of 36 and 48.

Partner Share! Example 4 Continued Find the common Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36 factors of 36 and 48. Factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48 The GCF of 36 and 48 is 12. The greatest possible number of CDs on each shelf is 12. Find the number of shelves of each type of CD when Adrianne puts the greatest number of CDs on each shelf.

36 pop CDs 12 CDs per shelf = 3 shelves 48 country CDs 12 CDs per shelf = 4 shelves When the greatest possible number of CD types are on each shelf, there are 7 shelves in total.

Lesson Review: Part I Write the prime factorization of each number. 1. 50 2 52 2. 84 22 3 7 Find the GCF of each pair of numbers. 3. 18 and 75 3 4. 20 and 36 4

Lesson Review: Part II Find the GCF each pair of monomials. 5. 12 x and 28 x 3 4 x 6. 27 x 2 and 45 x 3 y 2 9 x 2 7. Cindi is planting a rectangular flower bed with 40 orange flowers and 28 yellow flowers. She wants to plant them so that each row will have the same number of plants but of only one color. How many rows will Cindi need if she puts the greatest possible number of plants in each row? 17