Homework l l l Homework Assignment 30 Read

Homework l l l Homework Assignment #30 Read Section 4. 9 Page 282, Exercises: 1 – 13(Odd) Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

Homework, Page 282 Use Newton’s Method with the given function and initial value xo to calculate x 1, x 2, and x 3. Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

Homework, Page 282 Use Newton’s Method with the given function and initial value xo to calculate x 1, x 2, and x 3. Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

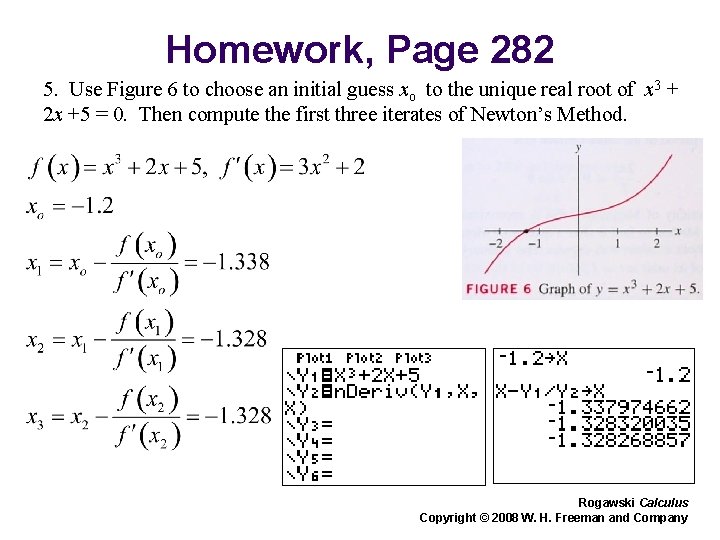
Homework, Page 282 5. Use Figure 6 to choose an initial guess xo to the unique real root of x 3 + 2 x +5 = 0. Then compute the first three iterates of Newton’s Method. Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

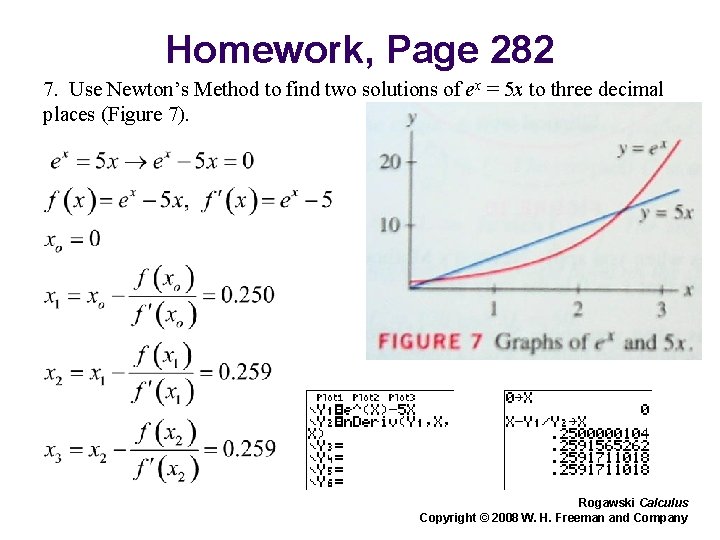
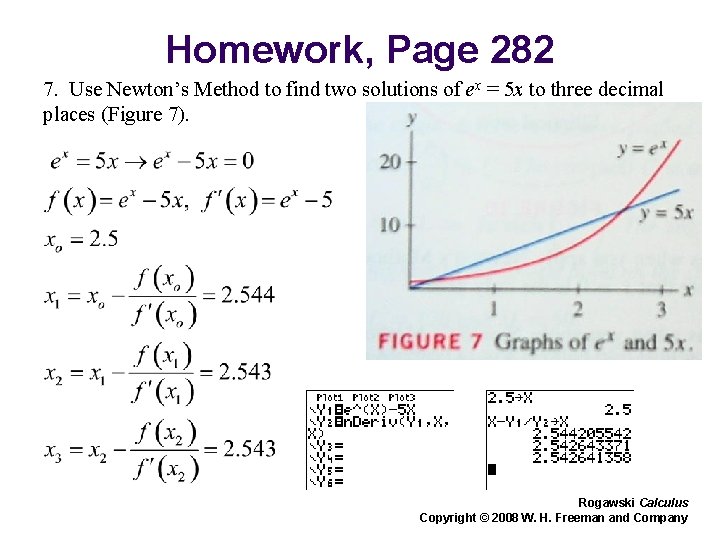
Homework, Page 282 7. Use Newton’s Method to find two solutions of ex = 5 x to three decimal places (Figure 7). Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

Homework, Page 282 7. Use Newton’s Method to find two solutions of ex = 5 x to three decimal places (Figure 7). Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

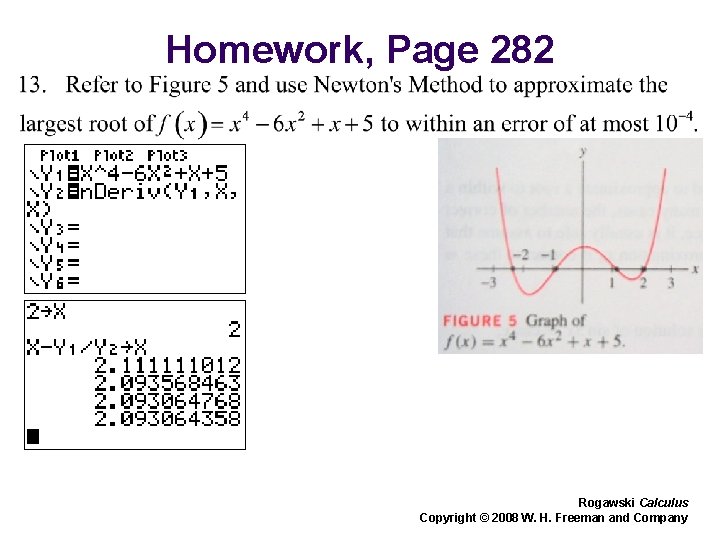
Homework, Page 282 Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

Homework, Page 282 Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

Homework, Page 282 Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

Jon Rogawski Calculus, ET First Edition Chapter 4: Applications of the Derivative Section 4. 9: Antiderivatives Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

In some cases, we may know the derivative and wish to find the function itself. A function F (x) whose derivative is f (x) is called an antiderivative of f (x). Theorem 1 gives us a method of finding the general antiderivative of a function, namely: Theorem 1 is proven as follows: Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

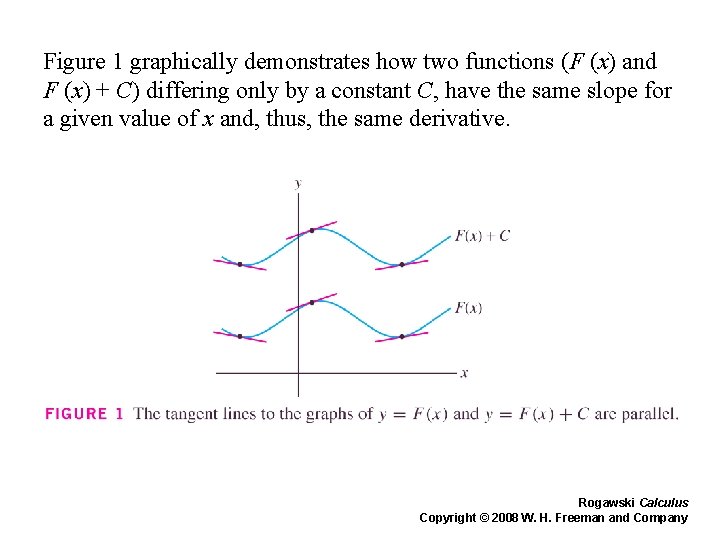
Figure 1 graphically demonstrates how two functions (F (x) and F (x) + C) differing only by a constant C, have the same slope for a given value of x and, thus, the same derivative. Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

The process of antidifferentiation is denoted by the Leibniz symbol ∫ which specifies finding the indefinite integral of a function. Just as we have rules for differentiation, we also have rules for integration, of which the first is: Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

Example, Page 292 Find the general antiderivative of f (x) and check your answer by differentiating. Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

Example, Page 292 Find the general antiderivative of f (x) and check your answer by differentiating. Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

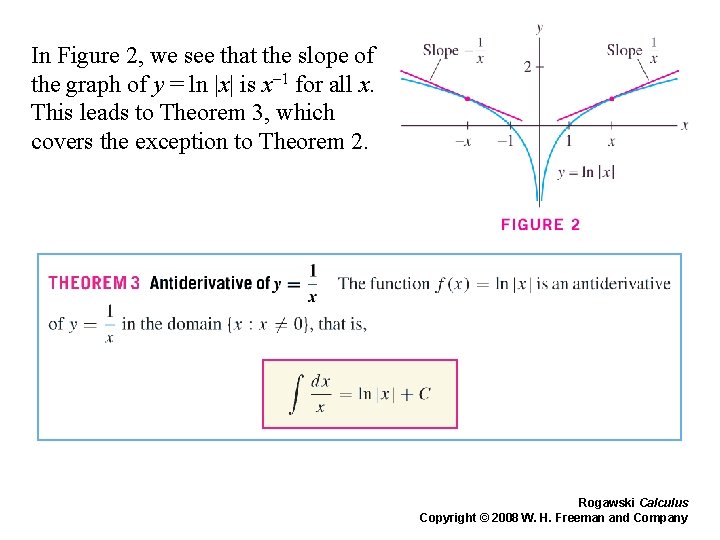
In Figure 2, we see that the slope of the graph of y = ln |x| is x– 1 for all x. This leads to Theorem 3, which covers the exception to Theorem 2. Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

The linearity rules for differentiation have their counterparts for integration as noted in Theorem 4. Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

Example, Page 292 Evaluate the indefinite integral. Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

Example, Page 292 Evaluate the indefinite integral. Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

Example, Page 292 Evaluate the indefinite integral. Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

Recalling derivatives of the basic trigonometric functions, we can recognize the basic trigonometric integrals. Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

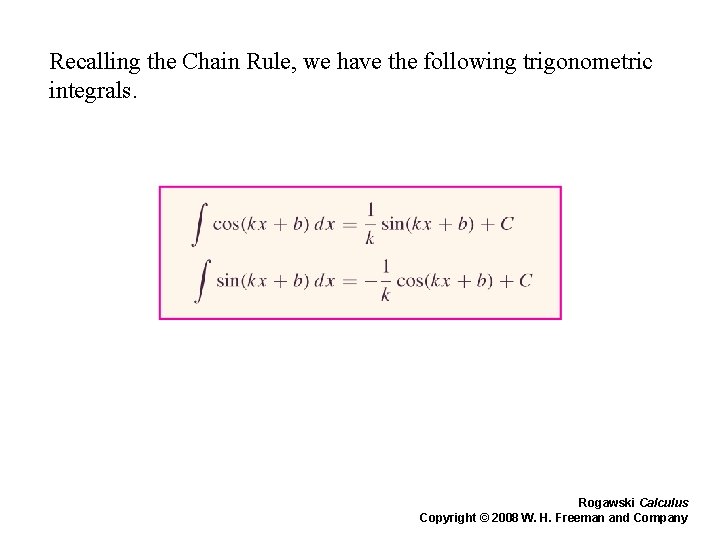
Recalling the Chain Rule, we have the following trigonometric integrals. Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

Example, Page 292 Evaluate the indefinite integral. Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

Example, Page 292 Evaluate the indefinite integral. Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

Remembering that the exponential function is its own derivative, we see how the indefinite integral of ex is ex + C. Applying the Chain rule in reverse to the exponential function, we obtain: Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

Example, Page 292 Evaluate the indefinite integral. Rogawski Calculus Copyright © 2008 W. H. Freeman and Company

Homework l l l Homework Assignment #31 Review Section 4. 9 Page 292, Exercises: 1 – 41(EOO) Rogawski Calculus Copyright © 2008 W. H. Freeman and Company