Hoe een Tom een sudoku oplost dr Arnold

Hoe een Tom een sudoku oplost dr. Arnold Meijster a. meijster@rug. nl

Palindromen Opdracht: Ga van een willekeurig woord na, of het een palindroom is of niet. ➲ ➲ ➲ ➲ lol pop lepel negen droomoord parterretrap meetsysteem

Algoritme: Palindromen L links E P E L rechts Zet links bij het eerste teken Zet rechts bij het laatste teken HERHAAL ALS teken bij links verschilt van teken bij rechts DAN UITVOER geen palindroom STOP ANDERS links 1 naar rechts 1 naar links TOTDAT links >= rechts UITVOER wel palindroom

Palindromen: Een iets andere kijk op de zaak Een ‘tekst’ met nul tekens is een palindroom. Een ‘tekst’ met 1 teken is een palindroom. Een ‘tekst’ a. Xa is alleen palindroom als X een palindroom is. Een ‘tekst’ a. Xb is geen palindroom.

Recursie ➲ Recursie = zelf-referentie. ➲ Recursie is een alternatief voor herhaling. ➲ Vaak is recursie een natuurlijke manier om ingewikkelde problemen op te lossen.

Google eens naar recursie ; -)

Faculteitsfunctie Basisgeval: 0! = 1 Recursiegeval: n! = n*(n-1)! Reeks: 1, 1, 2, 6, 24, 120, 720, 5040, 40320, …. 4! = = = = = 4*(4 -1)! 4*3*(3 -1)! 12*2*(2 -1)! 24*1*(1 -1)! 24*0! 24*1 24 int fac(int n) { if (n == 0) return 1; return n*fac(n-1)); }

Het Divide & Conquer Paradigma Divide et impera ➲ Als we een klein probleem hebben, dan lossen we het probleem direct op. (BASISGEVAL. ) ➲ Bij een groter problem, splitsen we het probleem in een aantal kleinere deelproblemen. (DIVIDE. ) ➲ Los elk van deze deelproblemen onafhankelijk van elkaar op (recursief). ➲ Combineer de deeloplossingen tot een oplossing van het hele probleem. (CONQUER. )

Recursie = Lui zijn!?

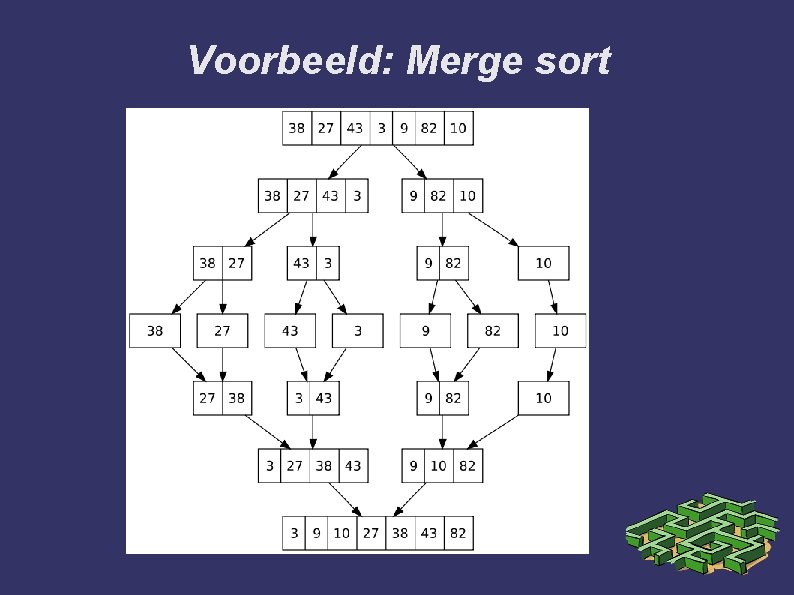
Pakje kaarten sorteren: instructies ➲ Verdeel: Ontvang een stapeltje kaarten Als het ‘stapeltje’ 1 kaart bevat, geef het dan direct terug. Anders: ➲ Splits het stapeltje in twee (ongeveer gelijke) helften Geef de eerste helft aan de (achter)buurman. Geef de tweede helft aan de (achter)buurman. Heers: Ontvang van je buren twee stapeltjes Herhaal totdat de kaarten op zijn: Vergelijk de top van de twee ontvangen stapeltjes Kies de grootste en leg onderaan een nieuwe stapel Geef de ‘nieuwe’ stapel terug.

Voorbeeld: Merge sort

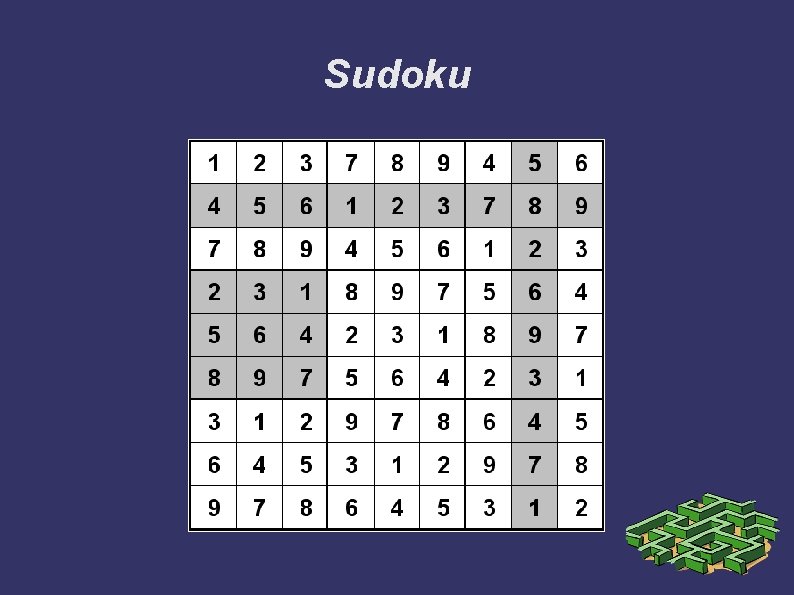
Sudoku

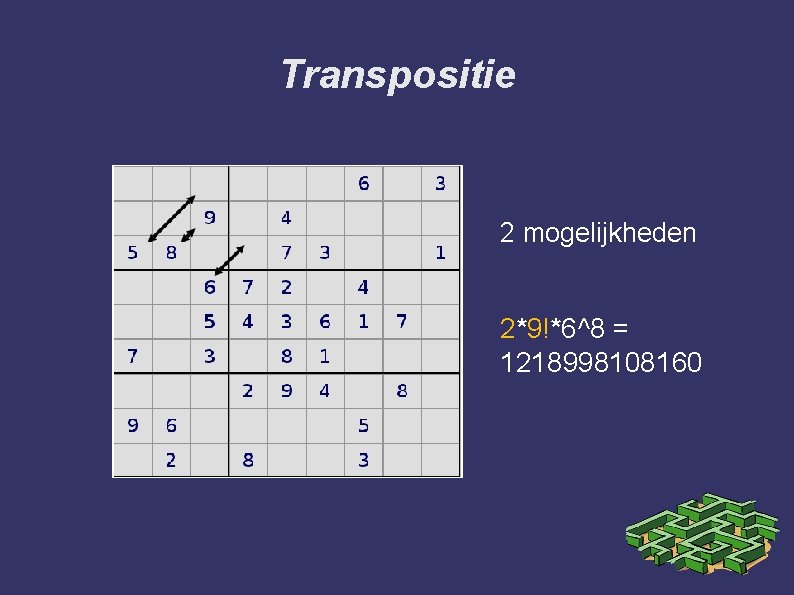
Equivalente sudokus ➲ Voor iedere sudoku bestaan er 1218998108160 equivalente sudokus. ➲ 2*9!*6^8 = 1218998108160 ➲ De factor 9! is eenvoudig te verklaren. Immers, verwissel maar eens een cijfer met een ander cijfer. Je hebt dan nog steeds een sudoku.

Transpositie 2 mogelijkheden 2*9!*6^8 = 1218998108160

rij/kolom verwisselingen Binnen een blok van drie aaneengesloten rijen/kolommen mag je vrijelijk verwisselen. Dit levert 3!=6 mogelijkheden. Totaal dus 6^6 mogelijkheden voor de gehele sudoku. 2*9!*6^8 = 2*9!*6^6*6^2= 1218998108160

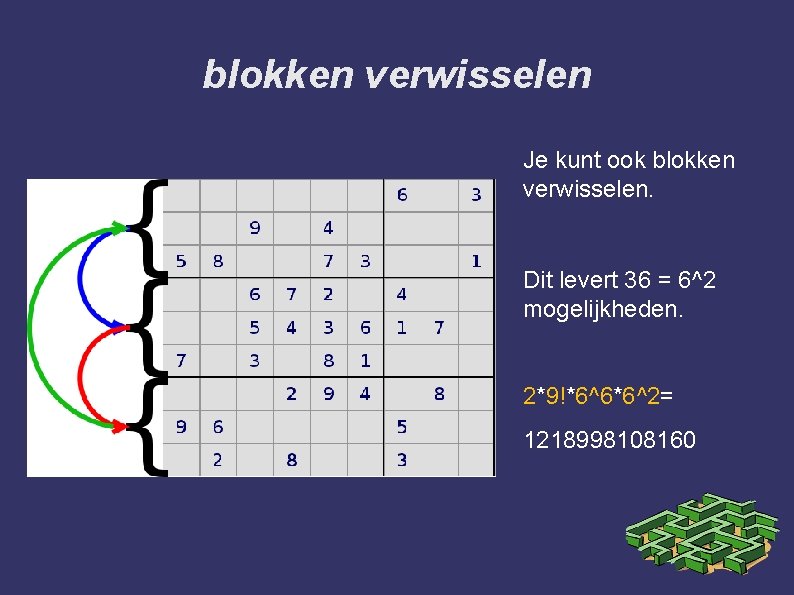
blokken verwisselen Je kunt ook blokken verwisselen. Dit levert 36 = 6^2 mogelijkheden. 2*9!*6^6*6^2= 1218998108160

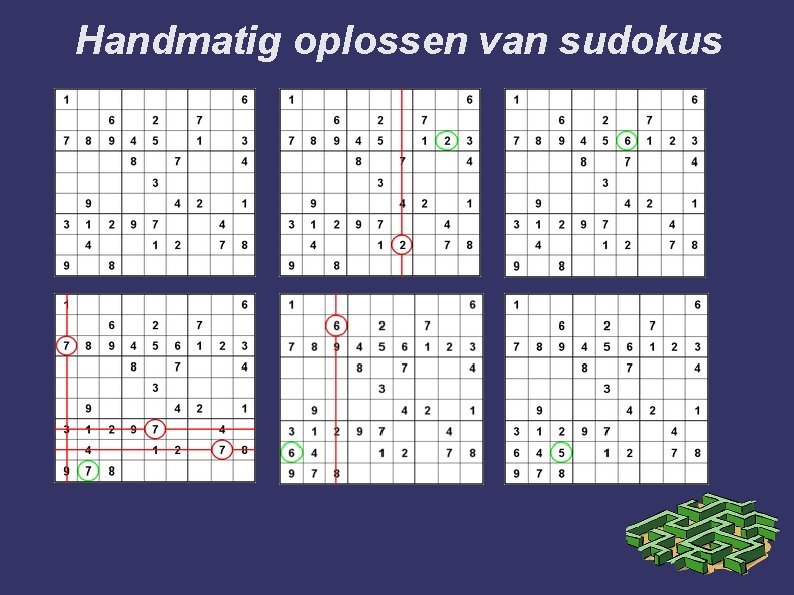
Handmatig oplossen van sudokus

Sudoku: recursieve oplossing ➲ Strategie: Voor ieder vakje dat nog niet ingevuld is, kies een cijfer. Controleer of dit cijfer kan/mag volgens de regels. Zo ja, vul in, en los de nu ontstane puzzel op (indien mogelijk). Dit is een kleinere versie van het oorspronkelijke probleem! Zo niet, kies een ander cijfer. Als geen enkele keuze mogelijk is, dan zitten we op een dood spoor. We gaan dan een stap terug naar het vorige beslissingspunt (backtracking).

Backtracking ➲ Strategie voor het ‘zoeken’ naar een oplossing. ➲ Volg een ‘route’ naar een oplossing totdat het duidelijk wordt dat langs deze weg geen oplossing gevonden kan worden. Op dit punt gaan we terug langs het pad (backtrack) tot we een punt hebben bereikt waar vanuit we weer verder kunnen zoeken naar een oplossing.

void losop(int rij, int kolom, int sudoku[9][9]) { int cijfer, r, k; /* basisgeval */ if (rij == 9) { toon. Oplossing(sudoku); return; } /* recursiegeval */ if (kolom < 8) { r = rij; k = kolom + 1; } else { r = rij + 1; k = 0; } if (sudoku[rij][kolom] != 0) { /* er is reeds een cijfer ingevuld, ga door */ losop(r, k, sudoku); } else { for (cijfer=1; cijfer < 10; cijfer++){ if (cijfer. Toegestaan(rij, kolom, cijfer, sudoku)) { /* vul het cijfer in en ga de recursie in */ sudoku[rij][kolom] = cijfer; losop(r, k, sudoku); /* maak het vakje weer leeg */ sudoku[rij][kolom] = 0; } }

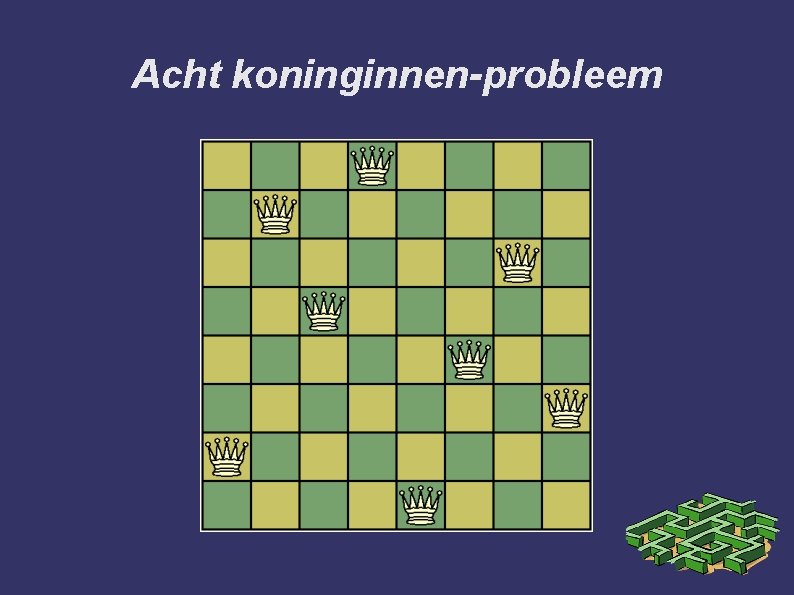
Acht koninginnen-probleem ➲ Vind alle configuraties van acht koninginnen op een schaakbord zodanig dat ze geen van allen een andere kunnen slaan.

Acht koninginnen-probleem

Acht koninginnen: uitputtend zoeken ➲ Genereer alle mogelijke combinaties en controleer voor ieder combinatie of het een oplossing is. ➲ Dit zijn (64!)/[(8!)(64 -8)!]=(64*63*62*61*60*59*58*57)/40320 = 4, 426, 165, 368 combinaties Eenvoudig verbetering: stop proberen als een oplossing toch niet mogelijk is.

Acht koninginnen-probleem ➲ 8 koninginnen, 8 rijen ➲ Dus, ➲ ➲ in elke rij moet een koningin geplaatst worden. in elke kolom moet een koningin geplaatst worden.

Acht koninginnen-probleem ➲ Recursieve oplossingstrategie: Iedere recursieve aanroep probeert een koningin te plaatsen in een specifieke rij i. Als dit lukt, ga dan recursief verder met rij i+1. Bij een aanroep is de toestand van het bord ten gevolge van eerdere aanroepen bekend (m. a. w. waar staan de andere koninginnen? ). Als alle mogelijke posities van een rij zijn geprobeerd, dan gaan we een stap terug (backtracking) en proberen andere mogelijkheden voor plaatsing op de voorgaande rij(en). Als het niet mogelijk blijkt een koningin te plaatsen op rij i, probeer dan niet verder te gaan met rij i+1 maar keer ook nu terug naar rij i-1 (backtrack). Het aantal te inspecteren posities is nu maximaal 8!=8*7*6*5*4*3*2= 40320.

Acht koninginnen-probleem ➲ Als een koningin op de positie (r, k) wordt geplaatst, dan bestrijkt zij: – de rij met nummer r – de kolom met nummer k – een stijgende ‘diagonaal’ door (r, k) – een dalende ‘diagonaal’ door (r, k) ➲ Coördinaten van een stijgende diagonaal voldoen aan k-r = constant. ➲ Coördinaten van een dalende diagonaal voldoen aan k + r = constant. ➲ We representeren de plaatsing van koninginnen op het bord in een rij pos. ➲ ➲ pos[r]=k betekent “in rij r staat een koningin in kolom k”. De keuze van de representatie van een bordconfiguratie geeft al dat we geen twee koninginnen in een kolom kunnen plaatsen.

Acht koninginnen - programma void plaats. Koningin(int rij, int pos[8]) { if (rij == 8) { /* basisgeval: klaar */ druk. Af(pos); } else { /* recursiegeval */ int r, kolom; for (kolom=0; kolom < 8; kolom++) { for (r=0; r < rij; r++) { if (pos[r] == kolom) { /* reeds koningin in deze kolom? */ break; } if (abs(pos[r]-kolom) == rij-r) { /* reeds koningin op diagonaal? */ break; } } if (r == rij) { /* veld is niet aangevallen, plaats koningin */ pos[rij] = kolom; plaats. Koningin(rij+1, pos); } } int main(int argc, char *argv[]) { int pos[8]; plaats. Koningin(0, pos); return 0; }

Het Handelsreizigersprobleem Gegeven: een lijst van steden die een handelsreiziger moet bezoeken, samen met de tabel van de afstanden tussen ieder paar van deze steden. Vind de kortste route waarbij de handelsreiziger iedere stad precies eenmaal bezoekt en eindigt waar hij begon.

Oplossingsmethode: TSP ➲ Laat aantal steden N=4 zijn: ➲ Genereer alle rijtjes beginnend met 1: 1, 2, 3, 4 1, 2, 4, 3 1, 3, 2, 4 1, 3, 4, 2 1, 4, 2, 3 1, 4, 3, 2 Bepaal voor ieder rijtje de lengte van de route en onthoud de kortste.

Oplossingsmethode: TSP ➲ Genereer vervolgens alle rijtjes beginnend met 2: 2, 1, 3, 4 2, 1, 4, 3 2, 3, 1, 4 2, 3, 4, 1 2, 4, 1, 3 2, 4, 3, 1 Enzovoorts. . .

Permutaties ➲ Je hebt 4 verschillende letters (A, B, C en D). Op hoeveel verschillende manieren kun je die permuteren? 4! = 4*3*2*1 = 24 7! = 5040 10! = 3. 628. 800

1998: CRPC Researchers Solve TSP for Record-Breaking 13, 509 Cities “CRPC Researchers (Rutgers University) have determined a breakthrough solution to the Traveling Salesman Problem (TSP), a method for finding an optimal path for a salesman to take when traveling through a specified number of cities. The researchers have solved the TSP for 13, 509 U. S. cities with populations of more than 500 people, a dramatic step beyond their previous record of 7, 397 cities, set in 1994. ”

Nog groter William Cook, a professor in Georgia Tech's School of Industrial and Systems Engineering, is a reigning champ of the traveling salesman problem. (2004: 24, 978 Swedish cities)

Grootst? http: //www. akira. ruc. dk/~keld/research/LKH/index-1. 3. html

Waar studeren? void vind. Universiteit(char *plaats) { if (strcmp(plaats, “groningen”) == 0) { /* basisgeval: klaar */ druk. Af(“GRONINGEN!n”); return; } else { /* recursiegeval */ int city; for (city=0; city<NCITIES; city++) { if (buurgemeente(plaats, plaatsnaam[city])) { vind. Universiteit(plaatsnaam[city]); } } int main(int argc, char *argv[]) { vind. Universiteit(“Waar ben ik? ”); return 0; }