Hodograph Turtles Tao Ju Ron Goldman Rice University

Hodograph Turtles Tao Ju, Ron Goldman Rice University

Introduction LOGO n n Drawing with FORWARD and TURN Polygons, stars, … and fractals Turtle Geometry n n Local and coordinate free geometry Morphing, L-systems, Plant modeling, theory of relativity…

Classical Turtle state: Position (P), Direction (w) Turtle commands: n n n FORWARD d Pnew = P + d w TURN a w 1 new = w 1 cos(a) - w 2 sin(a) w 2 new = w 1 sin(a) + w 2 cos(a) PEN_UP, PEN_DOWN w P

Classical Turtle program n n n Initial state: P = {0, 0} and w = {1, 0} Sequence of turtle commands Plots the trace of position P Turtle Program Turtle Geometry

Hodograph Turtle Motivation: Plot the trace of direction w n Hodograph: tangential trajectory Turtle state: Direction (w) n Not affected by FORWARD Command FORWARD 1: TURN /6: Classical Turtle P P w wnew w Pnew Hodograph Turtle w wnew w

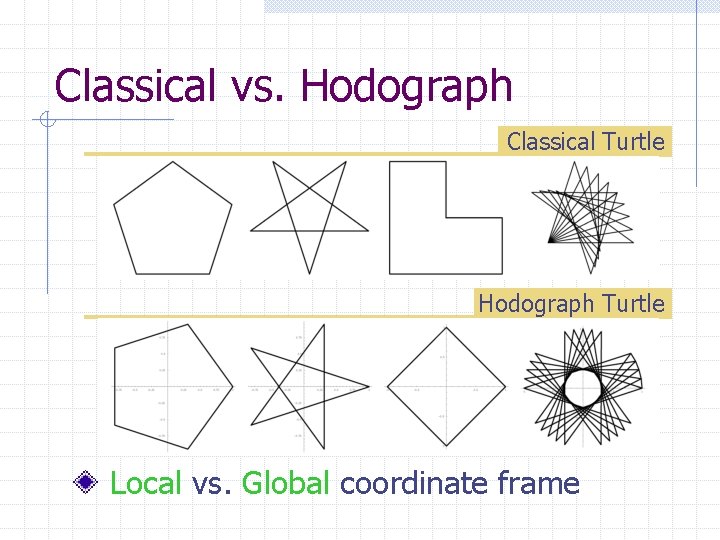
Classical vs. Hodograph Classical Turtle Hodograph Turtle Local vs. Global coordinate frame

Shapes Inscribed In Circles Hodograph turtle makes programming easier Rosette Classical Turtle Hodograph Turtle

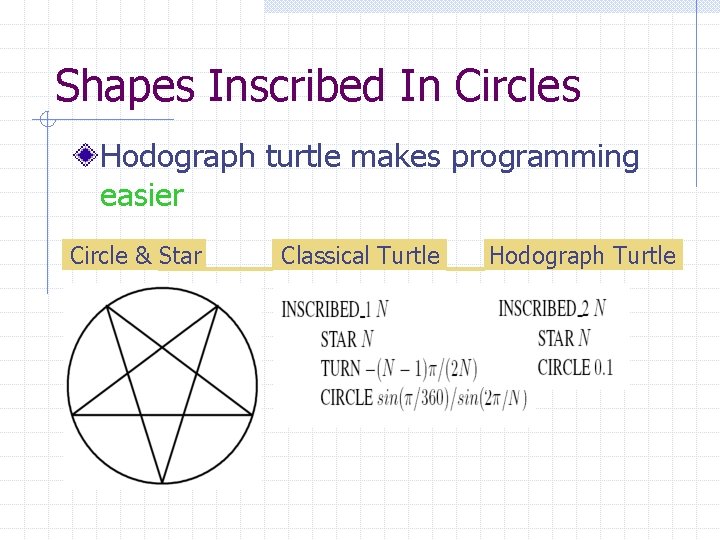
Shapes Inscribed In Circles Hodograph turtle makes programming easier Circle & Star Classical Turtle Hodograph Turtle

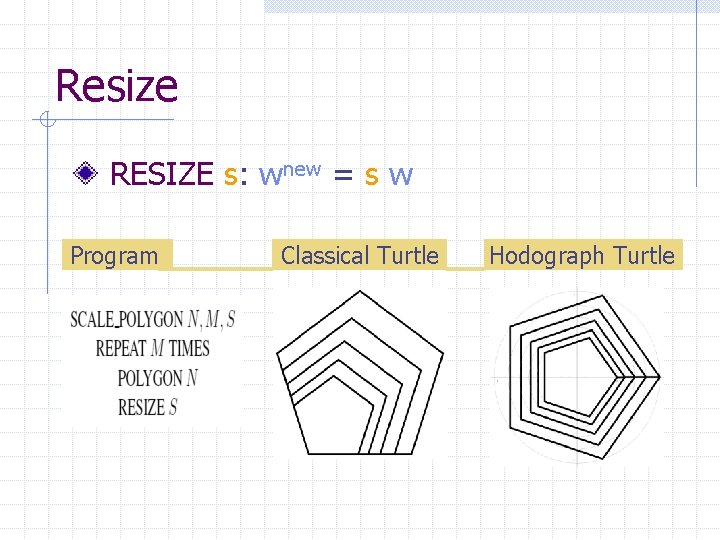
Resize RESIZE s: wnew = s w Program Classical Turtle Hodograph Turtle

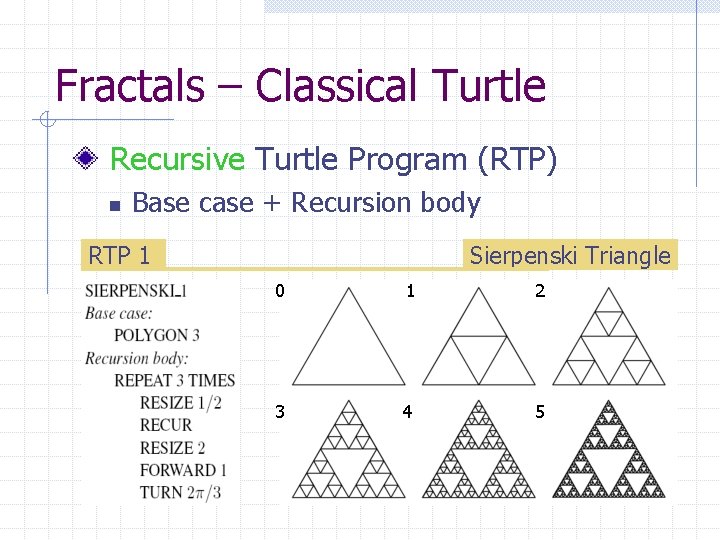
Fractals – Classical Turtle Recursive Turtle Program (RTP) n Base case + Recursion body RTP 1 Sierpenski Triangle 0 1 2 3 4 5

Fractals – Classical Turtle RTP 2 Sierpenski Triangle

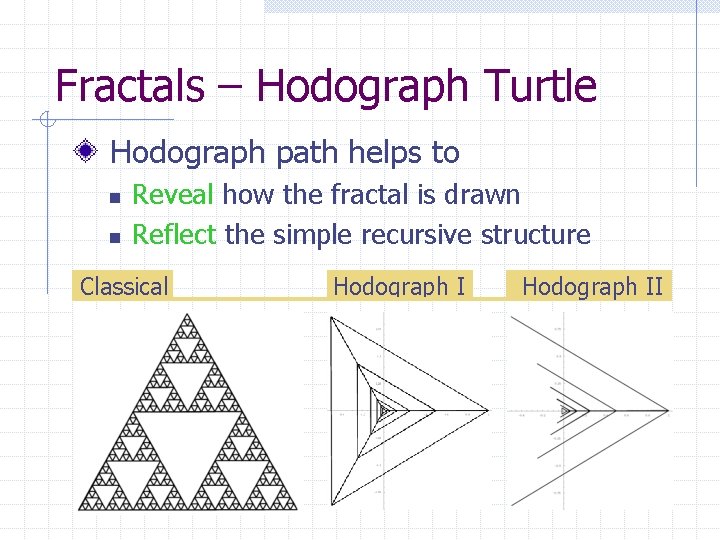
Fractals – Hodograph Turtle Hodograph path helps to n n Reveal how the fractal is drawn Reflect the simple recursive structure Classical Hodograph II

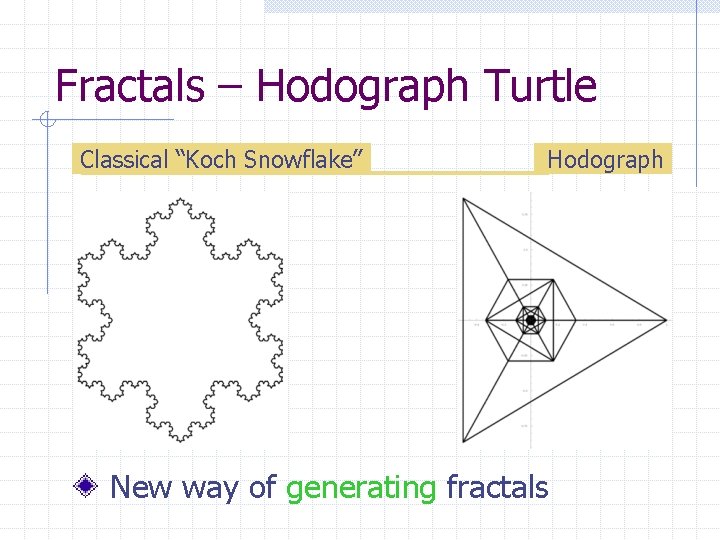
Fractals – Hodograph Turtle Classical “Koch Snowflake” Hodograph New way of generating fractals

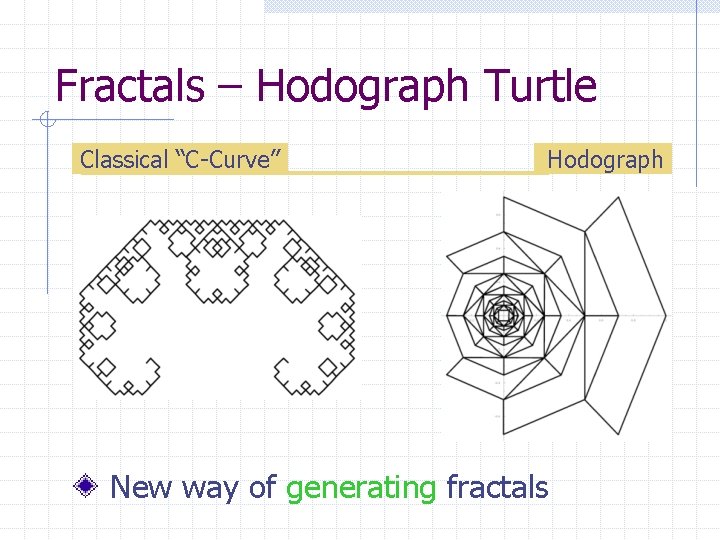
Fractals – Hodograph Turtle Classical “C-Curve” Hodograph New way of generating fractals

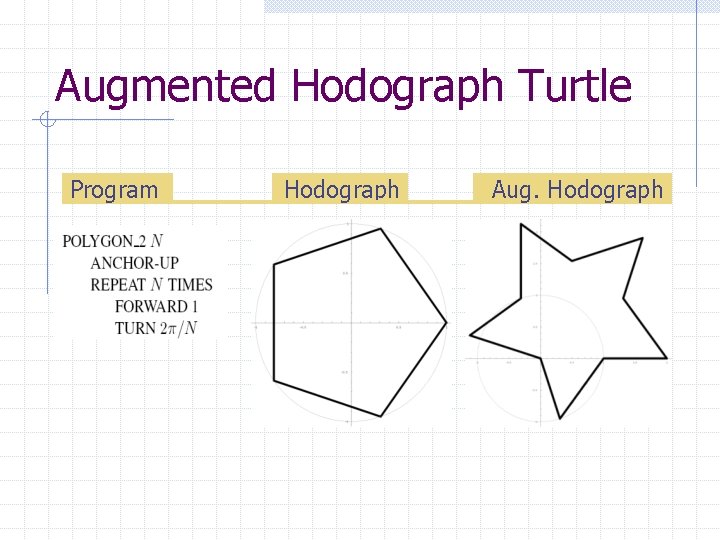
Anchor Commands Motivation: Free the poor creature being tethered to the origin) ! (from Augmented hodograph turtle (P’, w) n n Draws the trace of ( P’ + w ) Initial state: P’ = {0, 0} Anchor_Down: P’ stays fixed Anchor_Up: P’ moves with P

Augmented Hodograph Turtle Program Hodograph Aug. Hodograph

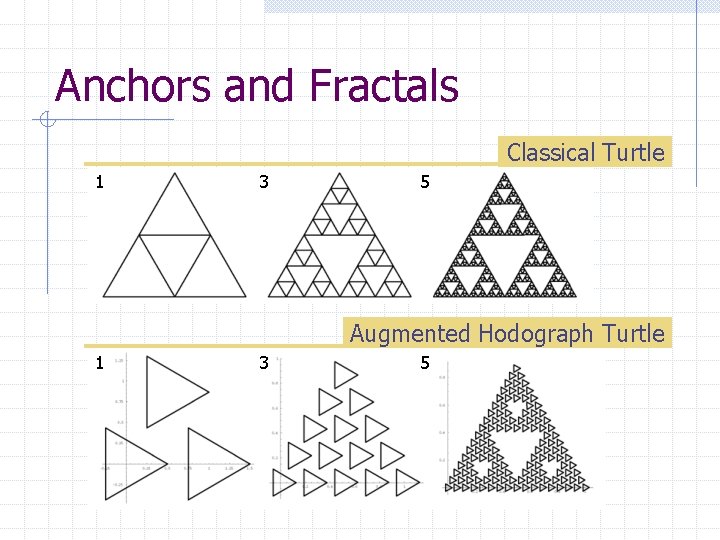
Anchors and Fractals The augmented hodograph turtle generates the same fractal in the limit as the classical turtle if : n n Both the pen and the anchor are up in the recursion body. In the base case, the pen is down and either w The anchor is up, or w The anchor is down and the turtle commands introduce no net change in the classical turtle's position vector P.

Anchors and Fractals Classical Turtle 1 3 5 Augmented Hodograph Turtle 1 3 5

Summary Classical Turtle Hodograph Augmented Turtle Hodograph turtle State P, w w P’, w Commands F, T, P, A Geometry Arbitrary Concentric Arbitrary Coordinate Frame Local Global Hybrid F: FORWARD, T: TURN, P: PEN, A: ANCHOR

Summary Hodograph turtles can n n Simplify drawing of shapes inscribed in circles Reveal how the classical turtle geometry is drawn Reflect recursive structure of turtle programs Generate new fractals As powerful as classical turtles !

Open Questions Extending theories of classical turtle to hodograph turtles n Looping Lemma, Space-time warping, nonconformal mappings, etc. Easier than classical turtle for teaching? n n No FORWARD command Single transformation: rotation