HNRS 227 Lecture 9 Chapter 9 Atomic Structure

HNRS 227 Lecture #9 Chapter 9 Atomic Structure presented by Prof. Geller 24 September 2002

Overview of Chapter 9 z. Atoms and atomic structure z. The Bohr Model z. Atomic Spectra z. Quantum Mechanics z. Electron Configurations z. Quarks

Atoms and Atomic Structure z. Atoms y“smallest” unit of matter z. Nucleus yprotons (positively charged) yneutrons (neutral) z. Electrons orbit nucleus ynegatively charged

Kirchoff’s Spectral Laws z. Kirchoff’s Spectral Laws (empirical) y. Continuous Spectrum xwhat produces them? y. Emission Spectrum xwhat produces them? y. Absorption Spectrum xwhat produces them?

Kirchoff’s First Spectral Law z. Any hot body produces a continuous spectrum yif it’s hot enough it looks something like this ydigitally like this Intensity Wavelength

Kirchoff’s Second Spectral Law z. Any gas to which energy is applied, either as heat or a high voltage, will produce an emission line spectrum like this yor digitally like this Intensity Wavelength

Kirchoff’s Third Spectral Law z. Any gas placed between a continuous spectrum source and the observer will produce a absorption line spectrum like this yor digitally like this Intensity Wavelength

The Photoelectric Effect z. A prelude to the Bohr atom yexperiment explained by Einstein, but performed by others xwhat caused this strange result?

Prelude to Bohr z. Einstein used Planck’s quantized particles yenergy of photon is related to frequency of light, not intensity xneed high enough frequency to get electrons released from metallic surface • E = h f

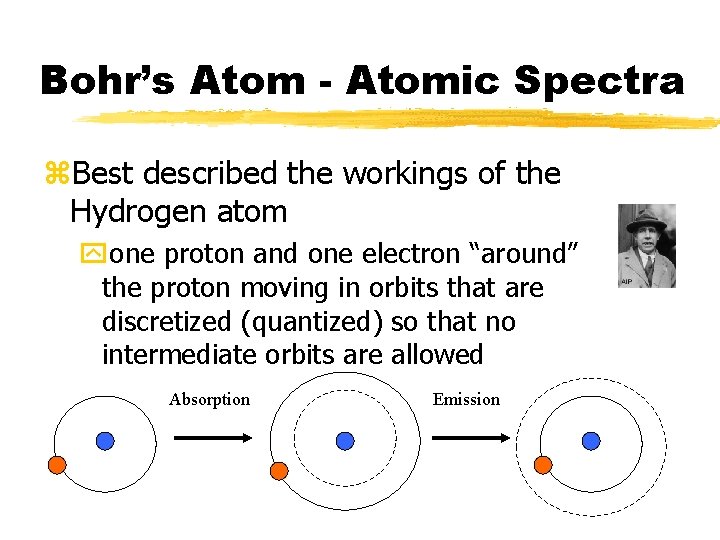
Bohr’s Atom - Atomic Spectra z. Best described the workings of the Hydrogen atom yone proton and one electron “around” the proton moving in orbits that are discretized (quantized) so that no intermediate orbits are allowed Absorption Emission

Quantum Mechanics and z. Duality of matter yact as waves or particles z. Matter waves y. De Broglie yl = h / m*v

Electron Configurations z. Atomic number = number of protons = number of electrons z. Pauli Exclusion Principle yno two electrons in an atom can have the same 4 quantum numbers xenergy level, sublevel, orientation, spin z. Heisenberg Uncertainty Principle ycan’t precisely measure both position and momentum

Quarks z. Too many subatomic particles ycould there be smaller particles z. Protons and neutrons consist of yquarks xhave partial charges • 1/3 and 2/3 z. Leptons - light particles like electrons z. Hadrons - heavy particles like protons ymade up of quarks