HMM Model Structure Presentation by Durga Yeluri What

HMM Model Structure Presentation by Durga Yeluri

What is the problem? l So far our assumptions l l Result of our assumptions l l Transitions are possible from any state to any other state Fully connected model “let the model find out itself” Bad model for any realistic problem, even with plenty of training data local maxima, but not over fitting Less constrained model More local maxima Solution ? ?

Model Topology l Construction based on l l Which transitions are allowed l Knowledge about the problem Disable transition from state k to state l by setting akl = 0. If the probability is zero, the number of transitions are also zero. Two types of modeling l l Duration Modeling Silent States Modeling

Duration Modeling l l When there is no change in the distribution for a certain length of the sequence Probability of a state transition to itself is p. Probability of leaving the state is (1 -p). P(l residues) = (1 -p)pl-1

Example l This model gives a minimum of 5 residues.

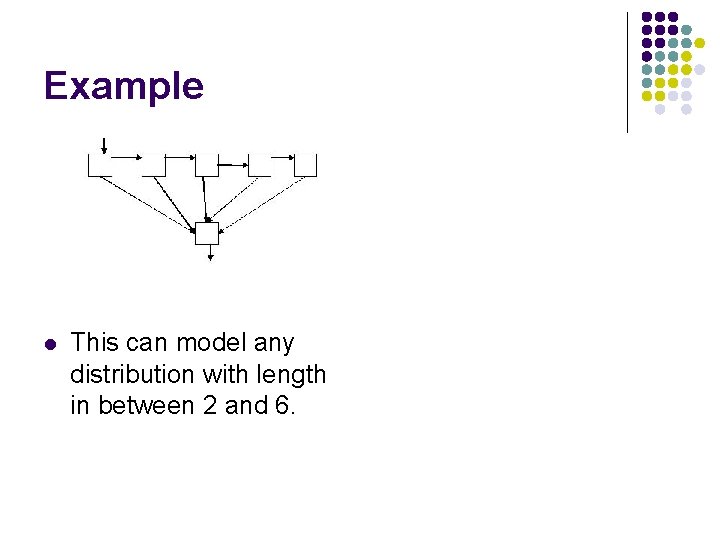
Example l This can model any distribution with length in between 2 and 6.

Example of Non-geometric length Distribution l l l Array of n states, smallest sequence length n. Probability of path with length l is pl-n (1 -p)n. The number of possible paths with length l is (l 1)choose(n-1).

Contd. . l l Total probability of all possible paths is P (l) = (l-1) choose (n-1) pl-n (1 -p)n. This is called negative binomial distribution.

Silent States l l l States which do not emit symbols in HMM Examples are begin and end states Also called null states Very useful in reducing the number of transitions in HMMs Leads to reduction in the number of parameters

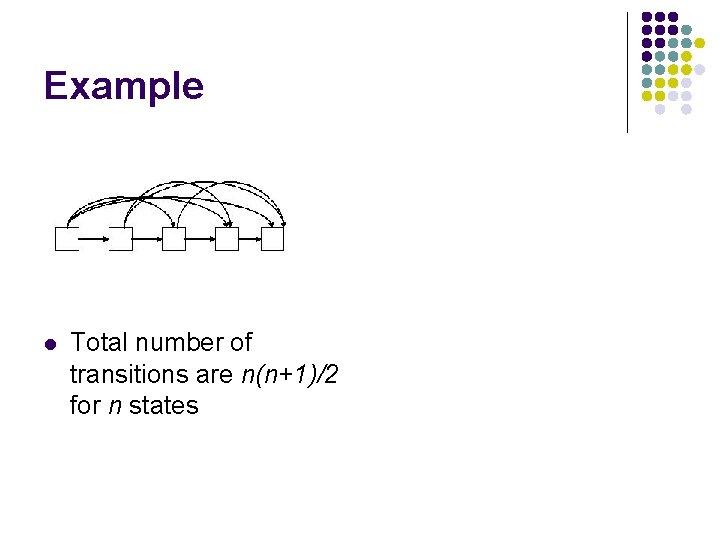
Example l Total number of transitions are n(n+1)/2 for n states

Reduction in the number of transitions with silent states l Total number of transitions for n states is nearly 3 n.

Discussion l l Total number of transitions with a length L in a forward connected model with out silent states? ? With silent states? ?

l Thank You!!!