Hiteltrlesztsi konstrukcik Ksztette Papp Jzsef Ksztette Papp Jzsef

Hiteltörlesztési konstrukciók Készítette: Papp József

Készítette: Papp József Hitel n Ha: felveszünk valamekkora összegű hitelt (Ht), akkor azt általában rendszeres időközönként Ct részletben törlesztenünk kell.

Készítette: Papp József Törlesztési terv n A törlesztési terv: A C 1, C 2, …, Cn pénzáramlás-sorozatot, tehát azokat a Ct összegeket és azok befizetési időpontjait tartalmazó táblázatot nevezzük törlesztési tervnek.

Készítette: Papp József Egyszerűsítés n Egyszerűsítés: Feltételezzük, hogy a hitel futamideje alatt, évente egyszer történik kamatfizetés, valamint tőketörlesztés!

Készítette: Papp József Törlesztő-részlet n A törlesztő-részlet: (Ct – adósság- szolgálat) az adós t-edik időpontban esedékes kötelezettsége, mely a t-edik időpontban esedékes kamatfizetés (Kt) és a t-edik időpontban esedékes tőketörlesztés (Tt) összegével egyenlő Ct = K t + T t

Készítette: Papp József Visszafizetendő hitel n. A visszafizetendő hitel: összege minden egyes törlesztő-részlet befizetése után csökken a befizetett TŐKETÖRLESZTÉS összegével!

Készítette: Papp József Hitelállomány n A hitelállomány: (tőketartozás) t-edik évi értéke megegyezik az előző időszakban esedékes tőketartozás és tőketörlesztés különbségével. Ht = Ht-1 – Tt-1 ha t >1

Készítette: Papp József Kamatfizetés n Az esedékes kamatfizetés: mértéke megegyezik az esedékes tőketartozás és hitelkamat (k) szorzatával. K t = Ht k

Készítette: Papp József Türelmi idő n A türelmi idő: az az idő, amely alatt még nincs tőketörlesztés. n Piaci hitelek esetén: k=r

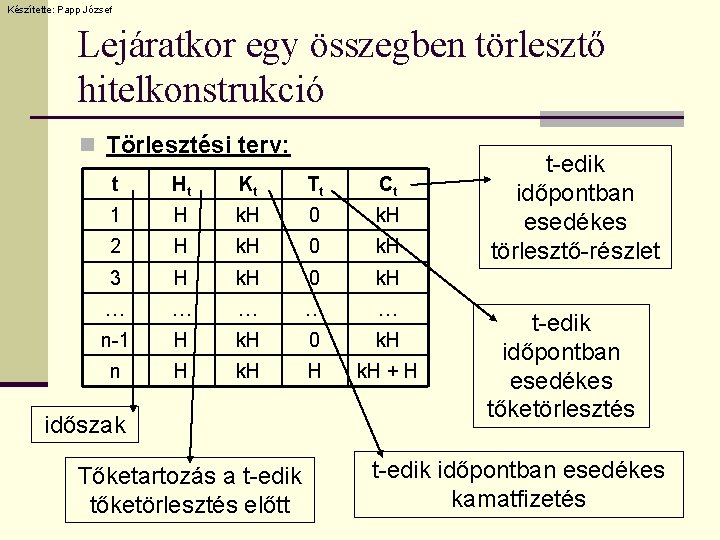
Készítette: Papp József Lejáratkor egy összegben törlesztő hitelkonstrukció n Jellemzői: n. A hitel lejáratakor esedékes a teljes tőketörlesztés. n Minden törlesztő-részlet - az utolsó kivételével – megegyezik a kamatfizetéssel.

Készítette: Papp József Lejáratkor egy összegben törlesztő hitelkonstrukció n Törlesztési terv: t Ht Kt Tt Ct 1 H k. H 0 k. H 2 H k. H 0 k. H 3 H k. H 0 k. H … … … n-1 H k. H 0 k. H n H k. H + H időszak Tőketartozás a t-edik tőketörlesztés előtt t-edik időpontban esedékes törlesztő-részlet t-edik időpontban esedékes tőketörlesztés t-edik időpontban esedékes kamatfizetés

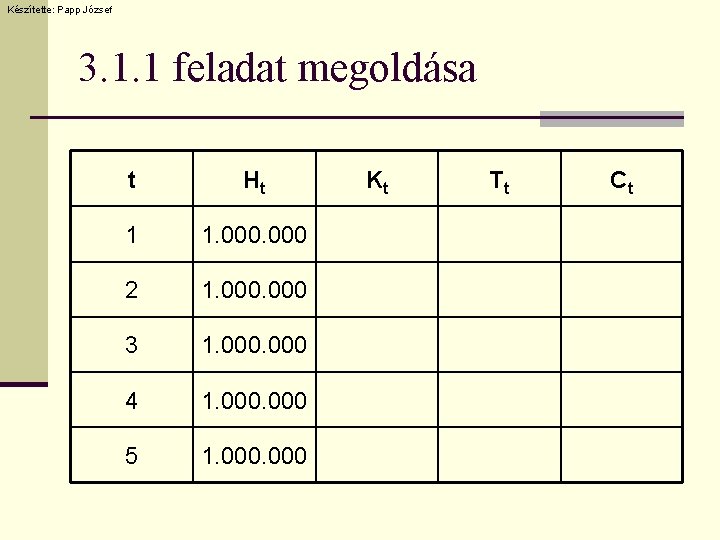
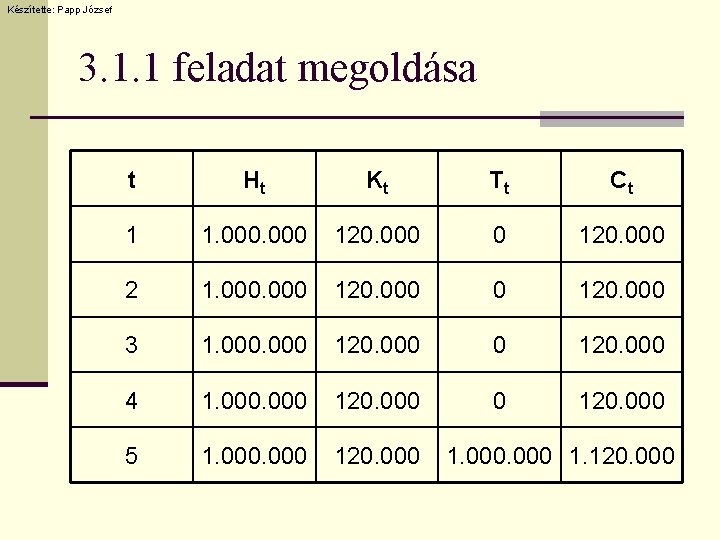
Készítette: Papp József 3. 1. 1 feladat n Írja fel annak a hitelkonstrukciónak a pénzáramlását, amelynek futamideje 5 év, névleges kamatlába évente egyszeri kamatfizetés mellett évi 12%, a hitel összege 1. 000 forint, a tőke visszafizetése lejáratkor egy összegben esedékes!

Készítette: Papp József 3. 1. 1 feladat megoldása t Ht 1 1. 000 2 1. 000 3 1. 000 4 1. 000 5 1. 000 Kt Tt Ct

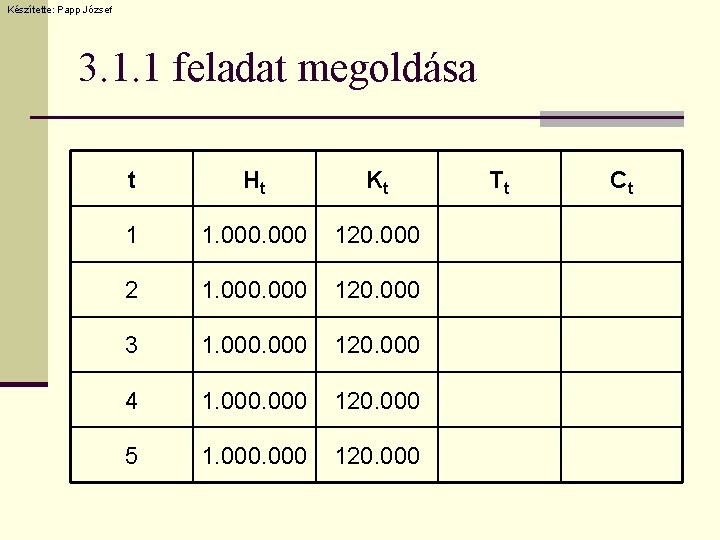
Készítette: Papp József 3. 1. 1 feladat megoldása t Ht Kt 1 1. 000 120. 000 2 1. 000 120. 000 3 1. 000 120. 000 4 1. 000 120. 000 5 1. 000 120. 000 Tt Ct

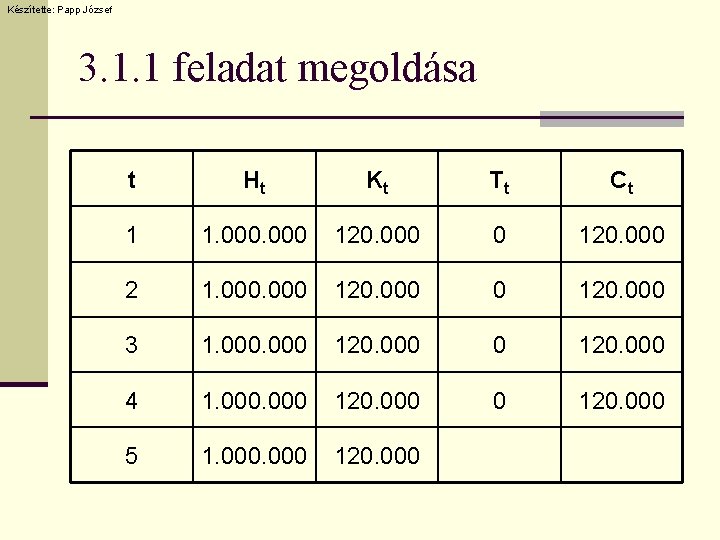
Készítette: Papp József 3. 1. 1 feladat megoldása t Ht Kt Tt Ct 1 1. 000 120. 000 2 1. 000 120. 000 3 1. 000 120. 000 4 1. 000 120. 000 5 1. 000 120. 000

Készítette: Papp József 3. 1. 1 feladat megoldása t Ht Kt Tt Ct 1 1. 000 120. 000 2 1. 000 120. 000 3 1. 000 120. 000 4 1. 000 120. 000 5 1. 000 120. 000 1. 120. 000

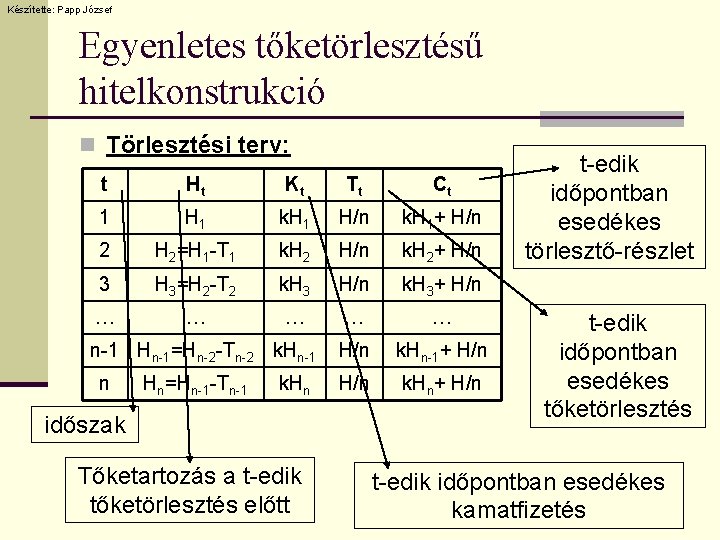
Készítette: Papp József Egyenletes tőketörlesztésű hitelkonstrukció n Jellemzői: n. A hitel törlesztése állandó nagyságú tőketörlesztő részletekben történik. n A fennálló hitelállomány a futamidő alatt minden periódusban azonos összeggel csökken, így a kamatfizetési kötelezettség a futamidő alatt lineárisan csökken.

Készítette: Papp József Egyenletes tőketörlesztésű hitelkonstrukció n Törlesztési terv: t Ht Kt Tt Ct 1 H 1 k. H 1 H/n k. H 1+ H/n 2 H 2=H 1 -T 1 k. H 2 H/n k. H 2+ H/n 3 H 3=H 2 -T 2 k. H 3 H/n k. H 3+ H/n … … … H/n k. Hn-1+ H/n k. Hn+ H/n n-1 Hn-1=Hn-2 -Tn-2 k. Hn-1 n Hn=Hn-1 -Tn-1 k. Hn időszak Tőketartozás a t-edik tőketörlesztés előtt t-edik időpontban esedékes törlesztő-részlet t-edik időpontban esedékes tőketörlesztés t-edik időpontban esedékes kamatfizetés

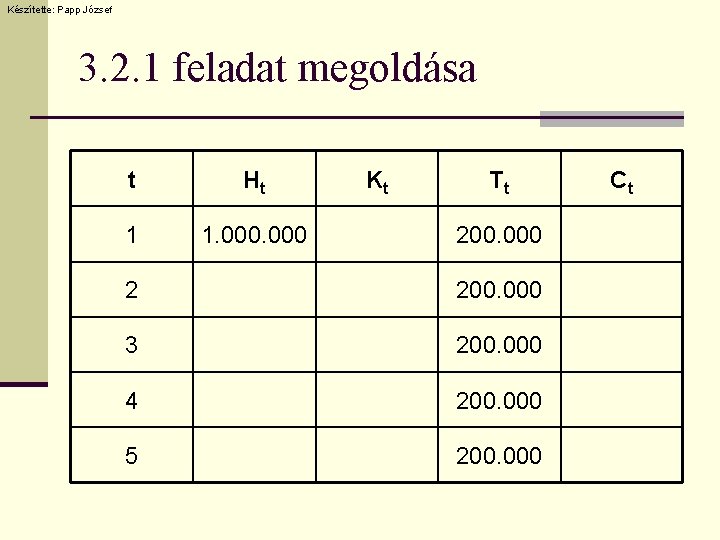
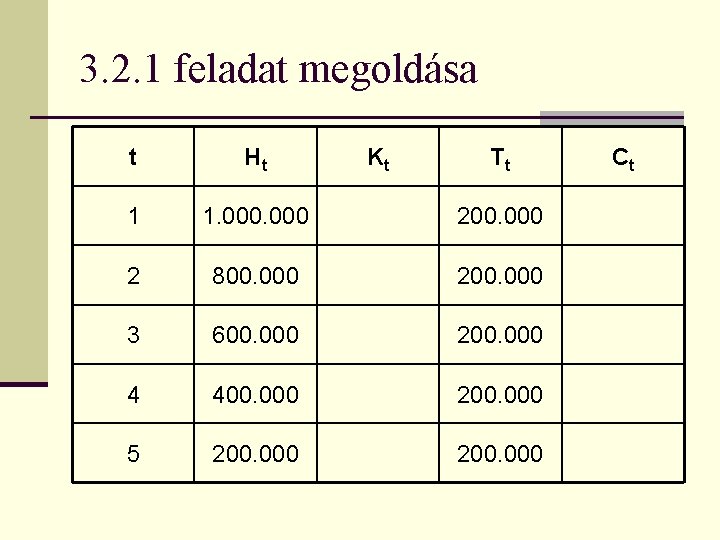
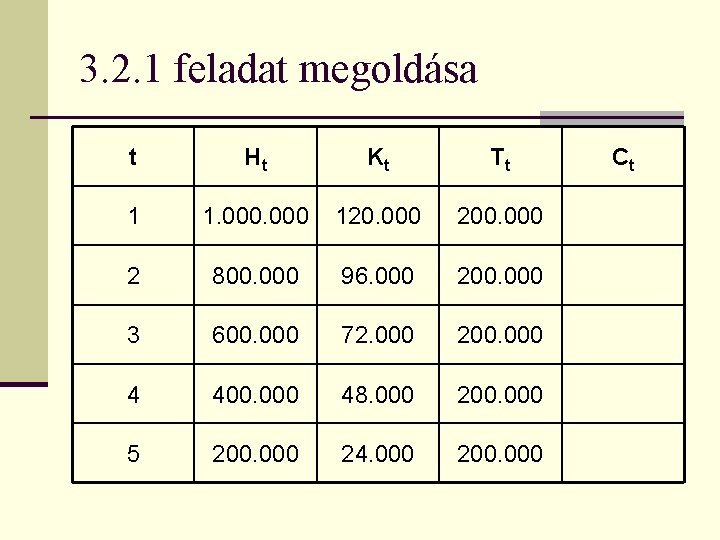
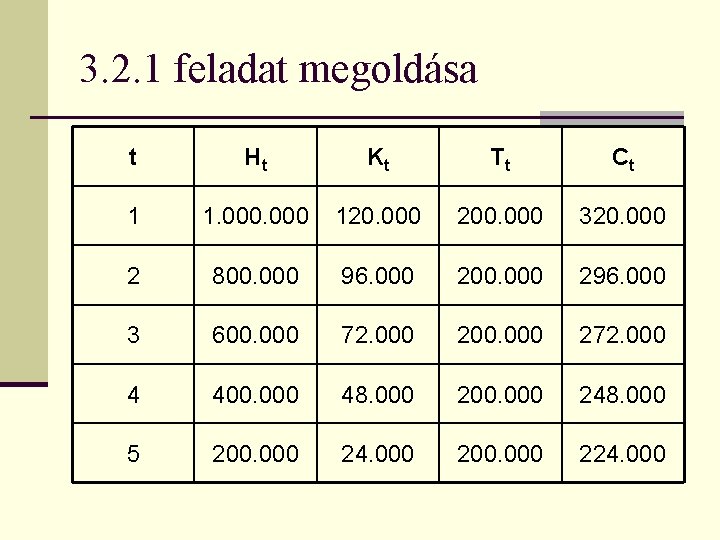
Készítette: Papp József 3. 2. 1 feladat n Írja fel annak a hitelkonstrukciónak a pénzáramlását, amelynek futamideje 5 év, névleges kamatlába évente egyszeri kamatfizetés mellett évi 12%, a hitel összege 1. 000 forint, a tőke visszafizetésére a futamidő alatt azonos részletekben kerül sor!

Készítette: Papp József 3. 2. 1 feladat megoldása t Ht 1 1. 000 Kt Tt 200. 000 2 200. 000 3 200. 000 4 200. 000 5 200. 000 Ct

3. 2. 1 feladat megoldása t Ht Kt Tt 1 1. 000 200. 000 2 800. 000 200. 000 3 600. 000 200. 000 4 400. 000 200. 000 5 200. 000 Ct

3. 2. 1 feladat megoldása t Ht Kt Tt 1 1. 000 120. 000 200. 000 2 800. 000 96. 000 200. 000 3 600. 000 72. 000 200. 000 4 400. 000 48. 000 200. 000 5 200. 000 24. 000 200. 000 Ct

3. 2. 1 feladat megoldása t Ht Kt Tt Ct 1 1. 000 120. 000 200. 000 320. 000 2 800. 000 96. 000 200. 000 296. 000 3 600. 000 72. 000 200. 000 272. 000 4 400. 000 48. 000 200. 000 248. 000 5 200. 000 24. 000 200. 000 224. 000

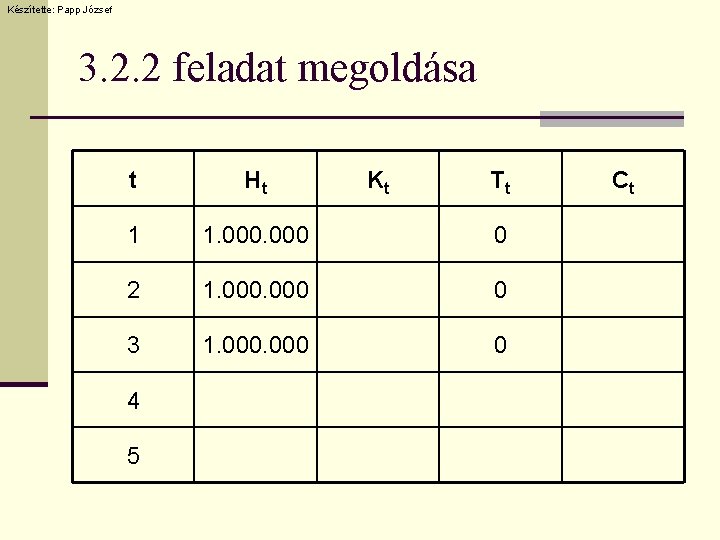
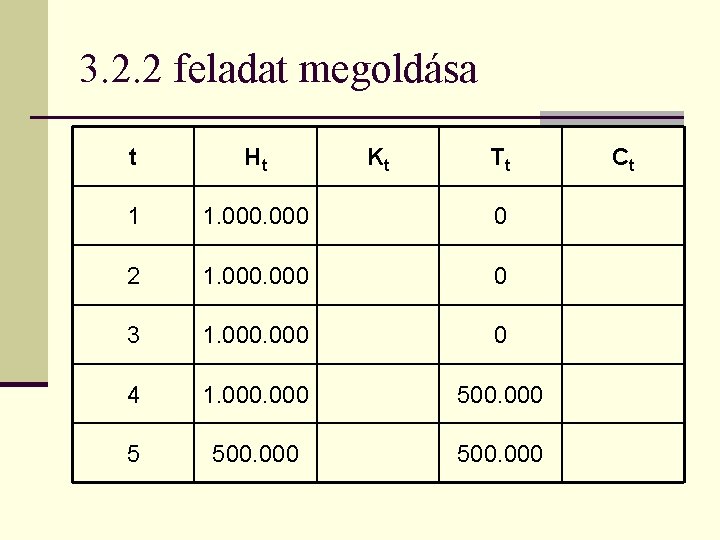
Készítette: Papp József 3. 2. 2 feladat n Írja fel annak a hitelkonstrukciónak a pénzáramlását, amelyek futamideje 5 év, a hitel névleges kamatlába évente egyszeri kamatfizetés mellett évi 12%, a hitel összege 1. 000 forint, valamint a tőketörlesztésre a futamidő alatt egyenletesen kerül sor 3 év türelmi idő után!

Készítette: Papp József 3. 2. 2 feladat megoldása t Ht 1 1. 000 0 2 1. 000 0 3 1. 000 0 4 5 Kt Tt Ct

3. 2. 2 feladat megoldása t Ht Kt Tt 1 1. 000 0 2 1. 000 0 3 1. 000 0 4 1. 000 500. 000 Ct

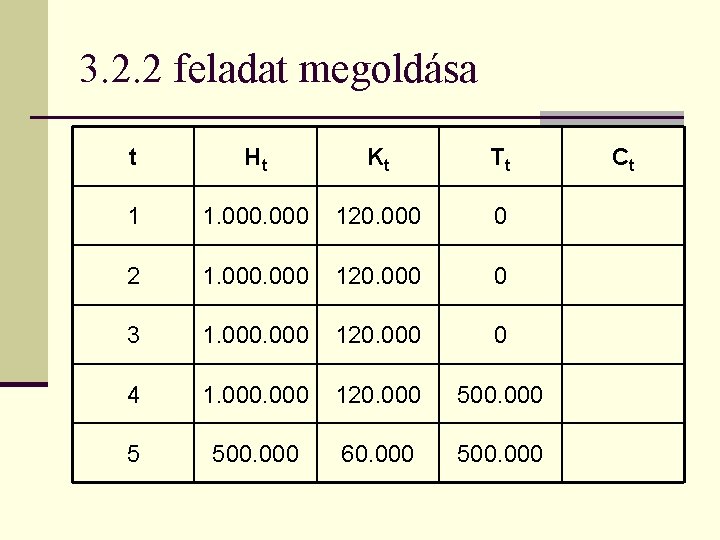
3. 2. 2 feladat megoldása t Ht Kt Tt 1 1. 000 120. 000 0 2 1. 000 120. 000 0 3 1. 000 120. 000 0 4 1. 000 120. 000 500. 000 5 500. 000 60. 000 500. 000 Ct

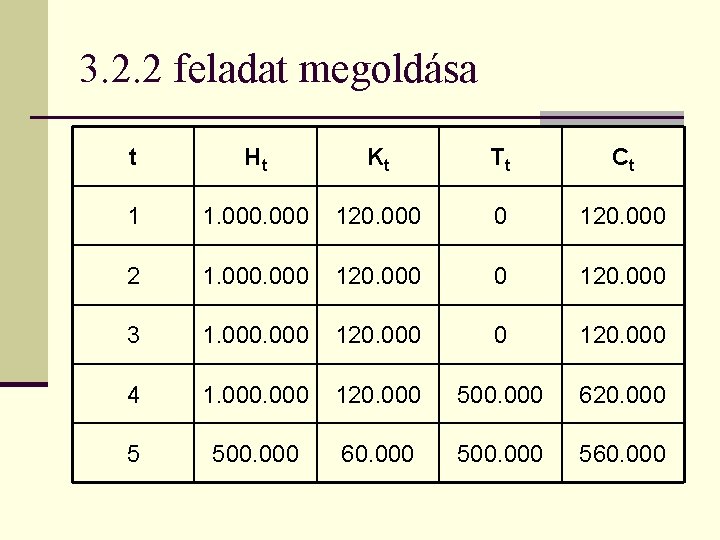
3. 2. 2 feladat megoldása t Ht Kt Tt Ct 1 1. 000 120. 000 2 1. 000 120. 000 3 1. 000 120. 000 4 1. 000 120. 000 500. 000 620. 000 5 500. 000 60. 000 500. 000 560. 000

Készítette: Papp József Azonos részletfizetésű (Annuitásos) hitelkonstrukció n Jellemzői: n. A törlesztő-részletek a kamatot és a tőketörlesztő részlet összegét tartalmazzák. n A futamidő alatt a kamat és a tőketörlesztő részletek összege állandó. (Azonos nagyságú törlesztő-részletek. )

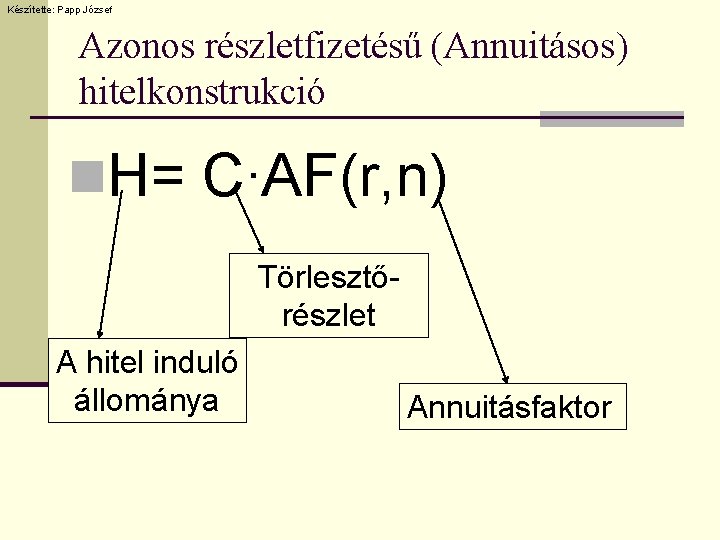
Készítette: Papp József Azonos részletfizetésű (Annuitásos) hitelkonstrukció n. H= C∙AF(r, n) Törlesztőrészlet A hitel induló állománya Annuitásfaktor

Készítette: Papp József Azonos részletfizetésű (Annuitásos) hitelkonstrukció A törlesztő-részlet nagysága: Az annuitásfaktor:

Készítette: Papp József Azonos részletfizetésű (Annuitásos) hitelkonstrukció A törlesztési terv kidolgozásának lépései: a törlesztő-részlet meghatározása Ø A kamatfizetés meghatározása Ø A tőketörlesztés meghatározása Ø

Készítette: Papp József 3. 3. 1 feladat n Egy 15 év futamidejű, azonos részletfizetésű hitel induló állománya 1. 000 Ft, kamatlába évi 17%. Mekkora a harmadik évi törlesztő részlet, illetve tőketörlesztő részlet?

Készítette: Papp József 3. 3. 1 feladat megoldása ü H = 1. 000 Ft ü t = 15 év n = 15 év ü r = 17% = 0, 17

3. 3. 1 feladat megoldása t Ht 1 1. 000 Kt Tt Ct 187. 822 2 187. 822 3 187. 822

3. 3. 1 feladat megoldása t Ht Kt 1 1. 000 170. 000 Tt Ct 187. 822 2 187. 822 3 187. 822

3. 3. 1 feladat megoldása t Ht Kt Tt Ct 1 1. 000 170. 000 17. 822 187. 822 3 187. 822

3. 3. 1 feladat megoldása t Ht Kt Tt Ct 1 1. 000 170. 000 17. 822 187. 822 2 982. 178 3 187. 822

3. 3. 1 feladat megoldása t Ht Kt Tt Ct 1 1. 000 170. 000 17. 822 187. 822 2 982. 178 166. 970 3 187. 822

3. 3. 1 feladat megoldása t Ht Kt Tt Ct 1 1. 000 170. 000 17. 822 187. 822 2 982. 178 166. 970 20. 852 187. 822 3 187. 822

3. 3. 1 feladat megoldása t Ht Kt Tt Ct 1 1. 000 170. 000 17. 822 187. 822 2 982. 178 166. 970 20. 852 187. 822 3 961. 326 187. 822

3. 3. 1 feladat megoldása t Ht Kt Tt Ct 1 1. 000 170. 000 17. 822 187. 822 2 982. 178 166. 970 20. 852 187. 822 3 961. 326 163. 425 187. 822

3. 3. 1 feladat megoldása t Ht Kt Tt Ct 1 1. 000 170. 000 17. 822 187. 822 2 982. 178 166. 970 20. 852 187. 822 3 961. 326 163. 425 24. 396 187. 822

Készítette: Papp József 3. 3. 2 feladat n Egy vállalkozás 72. 000 Ft hitelt vett fel egy kereskedelmi banktól, melynek feltételei a következők: n n n szerződés-kötéskori fix kamatláb: 16% a hitel törlesztési ideje: 10 év a visszafizetés évente egyenlő részletekben történik Számítsa ki, hogy a, Mennyi az évi törlesztő részlet összege, amely a kamatösszeget és a tőketörlesztést egyaránt tartalmazza? b, Az első évi törlesztő részletben milyen összegű a kamat, és milyen összegű a tőketörlesztés?

Készítette: Papp József 3. 3. 2 feladat megoldása ü H = 72. 000 Ft ü t = 10 év n = 10 év ü r = 16% = 0, 16

3. 3. 2 feladat megoldása t Ht 1 72. 000 Kt Tt Ct 14. 896. 878

3. 3. 2 feladat megoldása t Ht Kt 1 72. 000 11. 520. 000 Tt Ct 14. 896. 878

3. 3. 2 feladat megoldása t Ht Kt 1 72. 000 11. 520. 000 Tt Ct 3. 376. 878 14. 896. 878

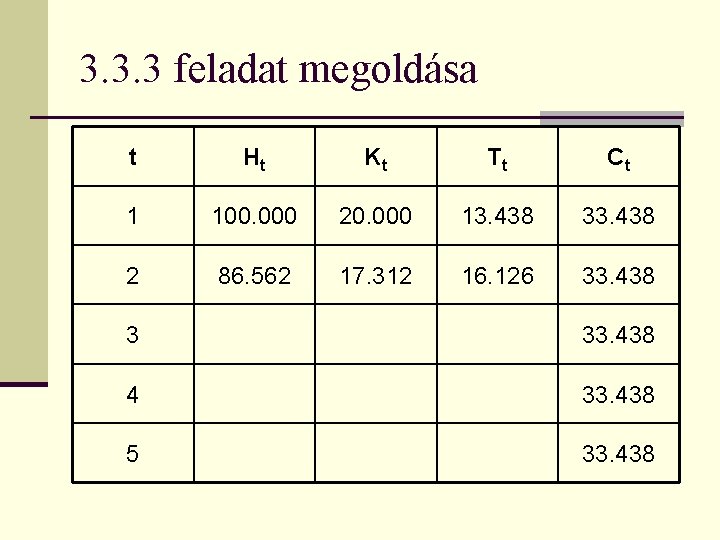
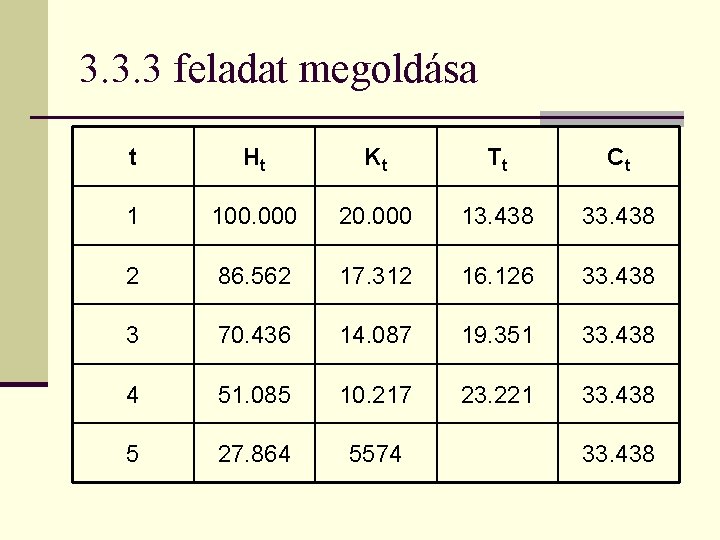
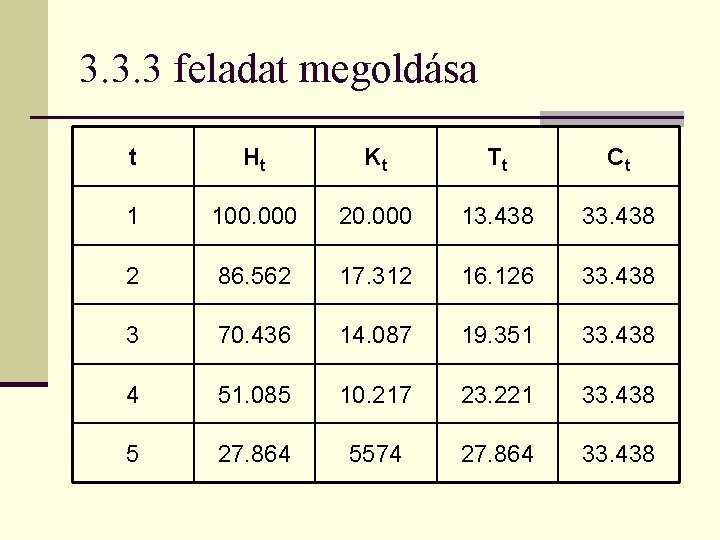
Készítette: Papp József 3. 3. 3 feladat n Írja fel annak a hitelkonstrukciónak a törlesztési tervét, amelynek futamideje 5 év, a hitel névleges kamatlába évente egyszeri kamatfizetés mellett évi 20%, a hitel folyósított összege 100. 000 Ft, és az éves törlesztő-részletek nagysága állandó.

Készítette: Papp József 3. 3. 3 feladat megoldása Határozzuk meg a rendelkezésre álló adatokat: ü H = 100. 000 Ft ü t = 5 év n = 5 év ü r = 20% = 0, 2

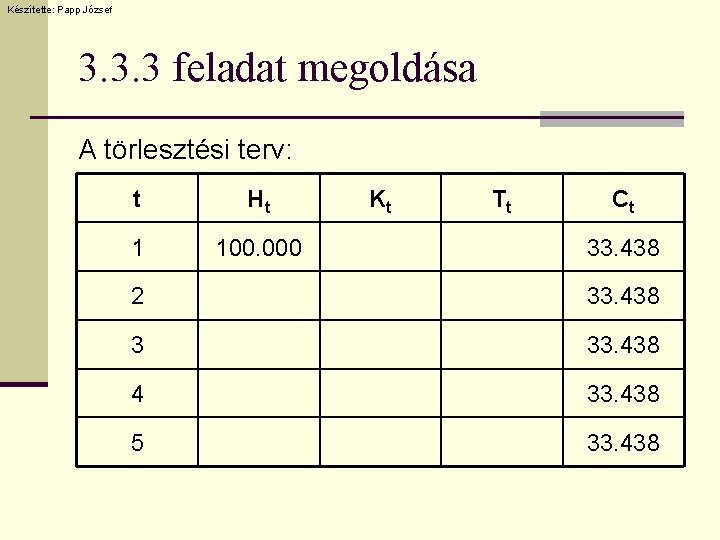
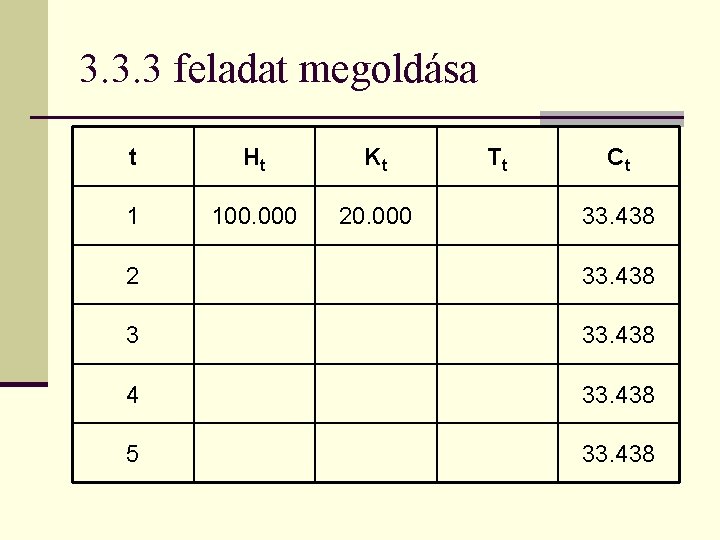
Készítette: Papp József 3. 3. 3 feladat megoldása A törlesztési terv: t Ht 1 100. 000 Kt Tt Ct 33. 438 2 33. 438 3 33. 438 4 33. 438 5 33. 438

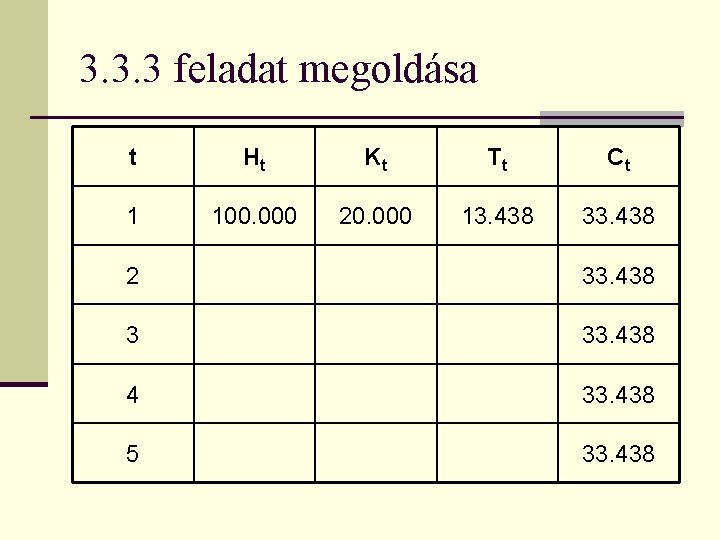
3. 3. 3 feladat megoldása t Ht Kt 1 100. 000 20. 000 Tt Ct 33. 438 2 33. 438 3 33. 438 4 33. 438 5 33. 438

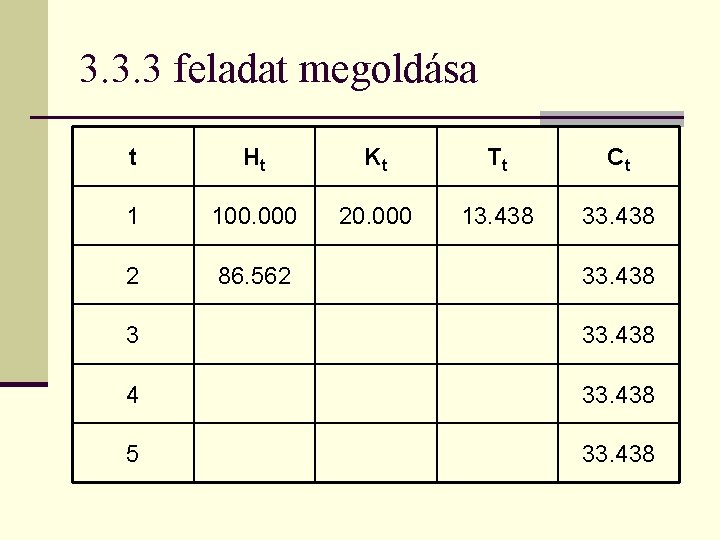
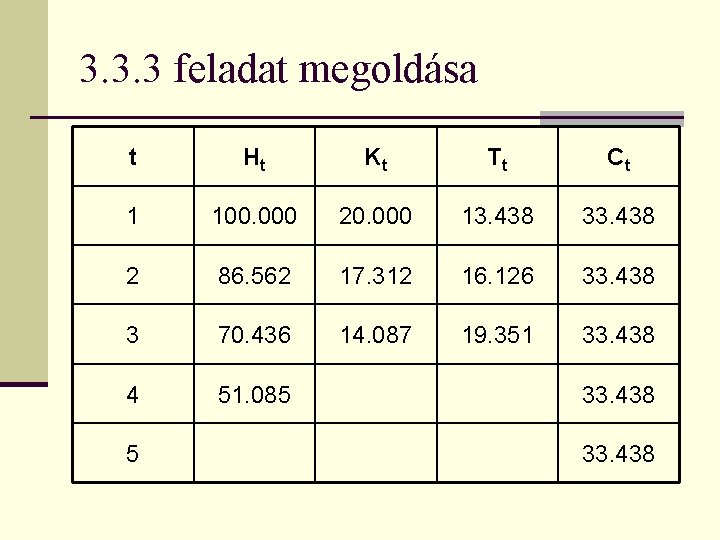
3. 3. 3 feladat megoldása t Ht Kt Tt Ct 1 100. 000 20. 000 13. 438 33. 438 2 33. 438 3 33. 438 4 33. 438 5 33. 438

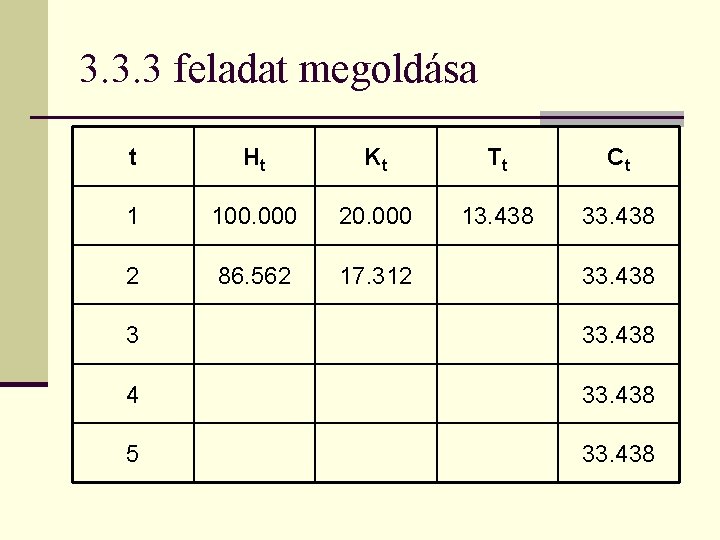
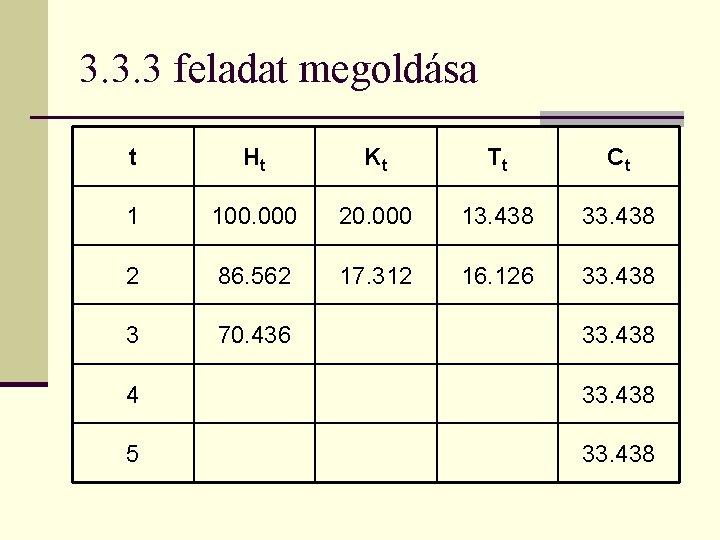
3. 3. 3 feladat megoldása t Ht Kt Tt Ct 1 100. 000 20. 000 13. 438 33. 438 2 86. 562 33. 438 3 33. 438 4 33. 438 5 33. 438

3. 3. 3 feladat megoldása t Ht Kt Tt Ct 1 100. 000 20. 000 13. 438 33. 438 2 86. 562 17. 312 33. 438 3 33. 438 4 33. 438 5 33. 438

3. 3. 3 feladat megoldása t Ht Kt Tt Ct 1 100. 000 20. 000 13. 438 33. 438 2 86. 562 17. 312 16. 126 33. 438 3 33. 438 4 33. 438 5 33. 438

3. 3. 3 feladat megoldása t Ht Kt Tt Ct 1 100. 000 20. 000 13. 438 33. 438 2 86. 562 17. 312 16. 126 33. 438 3 70. 436 33. 438 4 33. 438 5 33. 438

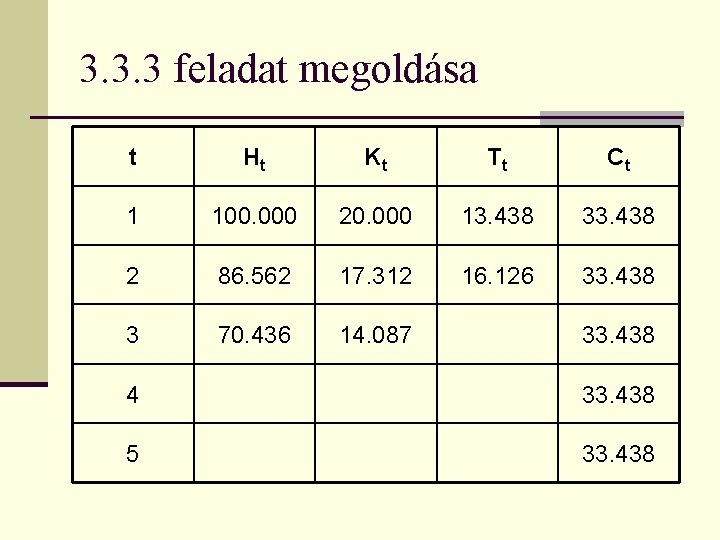
3. 3. 3 feladat megoldása t Ht Kt Tt Ct 1 100. 000 20. 000 13. 438 33. 438 2 86. 562 17. 312 16. 126 33. 438 3 70. 436 14. 087 33. 438 4 33. 438 5 33. 438

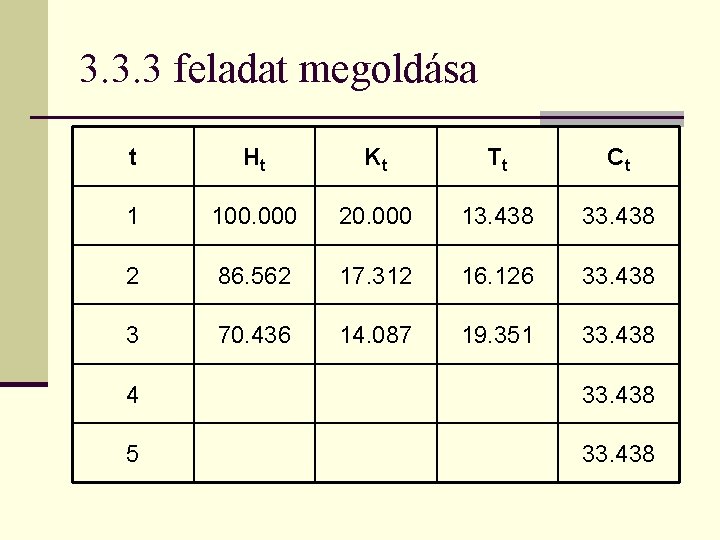
3. 3. 3 feladat megoldása t Ht Kt Tt Ct 1 100. 000 20. 000 13. 438 33. 438 2 86. 562 17. 312 16. 126 33. 438 3 70. 436 14. 087 19. 351 33. 438 4 33. 438 5 33. 438

3. 3. 3 feladat megoldása t Ht Kt Tt Ct 1 100. 000 20. 000 13. 438 33. 438 2 86. 562 17. 312 16. 126 33. 438 3 70. 436 14. 087 19. 351 33. 438 4 51. 085 5 33. 438

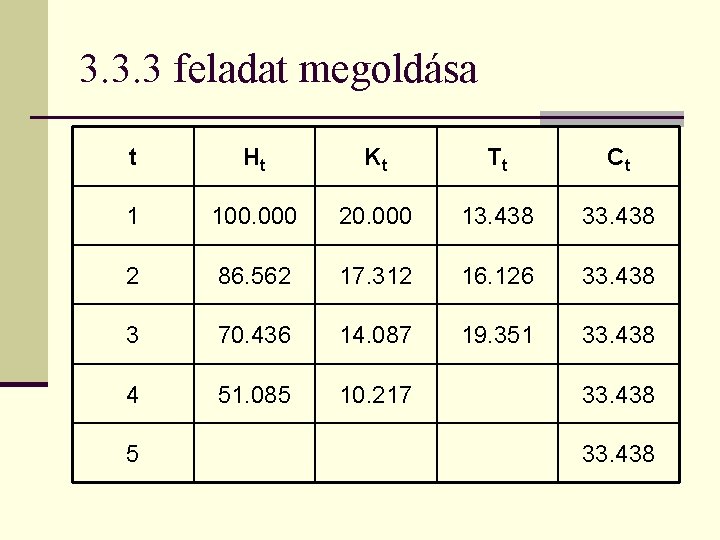
3. 3. 3 feladat megoldása t Ht Kt Tt Ct 1 100. 000 20. 000 13. 438 33. 438 2 86. 562 17. 312 16. 126 33. 438 3 70. 436 14. 087 19. 351 33. 438 4 51. 085 10. 217 5 33. 438

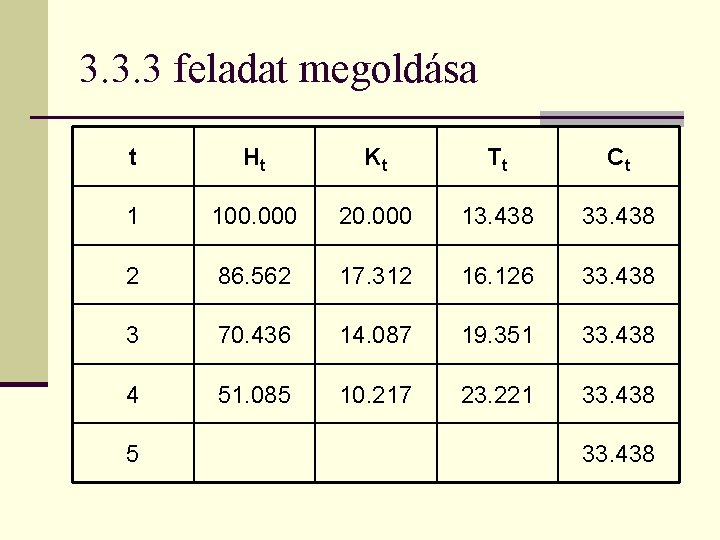
3. 3. 3 feladat megoldása t Ht Kt Tt Ct 1 100. 000 20. 000 13. 438 33. 438 2 86. 562 17. 312 16. 126 33. 438 3 70. 436 14. 087 19. 351 33. 438 4 51. 085 10. 217 23. 221 33. 438 5 33. 438

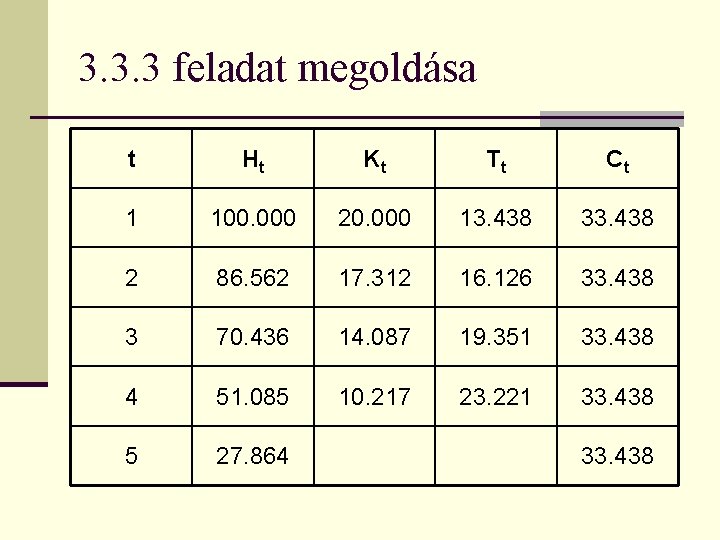
3. 3. 3 feladat megoldása t Ht Kt Tt Ct 1 100. 000 20. 000 13. 438 33. 438 2 86. 562 17. 312 16. 126 33. 438 3 70. 436 14. 087 19. 351 33. 438 4 51. 085 10. 217 23. 221 33. 438 5 27. 864 33. 438

3. 3. 3 feladat megoldása t Ht Kt Tt Ct 1 100. 000 20. 000 13. 438 33. 438 2 86. 562 17. 312 16. 126 33. 438 3 70. 436 14. 087 19. 351 33. 438 4 51. 085 10. 217 23. 221 33. 438 5 27. 864 5574 33. 438

3. 3. 3 feladat megoldása t Ht Kt Tt Ct 1 100. 000 20. 000 13. 438 33. 438 2 86. 562 17. 312 16. 126 33. 438 3 70. 436 14. 087 19. 351 33. 438 4 51. 085 10. 217 23. 221 33. 438 5 27. 864 5574 27. 864 33. 438

Készítette: Papp József 3. 3. 4 feladat n Mekkora éves törlesztő-részletet kell vállalnunk 5 év alatt, ha 1. 000 Ft hitelt veszünk fel, és a kölcsön effektív kamatlába évi 16%? Mekkora havi törlesztő-részletet kell vállalnunk?

Készítette: Papp József 3. 3. 4 feladat megoldása Határozzuk meg a rendelkezésre álló adatokat: ü H = 1. 000 Ft ü t = 5 év n = 5 év ü r = 16% = 0, 16

Készítette: Papp József 3. 3. 4 feladat megoldása Határozzuk meg a havi kamatlábat: t = 5 év n = 5 ∙ 12 hó = 60 db törlesztés

Készítette: Papp József 3. 3. 5 feladat n A 400. 000 Ft értékű számítógép 50%-át készpénzben egyenlíti ki. A fennmaradó 50%ot 24 hónap alatt fizeti ki havonta azonos törlesztő-részletek mellett. (Az első törlesztőrészlet 1 hónap múlva esedékes. ) A piaci hozam évi 13%. Mekkora összeget kell havonta fizetnie? n Mekkora 1 év elteltével a tőketartozása? n

Készítette: Papp József 3. 3. 5 feladat megoldása Határozzuk meg a rendelkezésre álló adatokat: ü H = 400. 000 Ft / 2 = 200. 000 Ft ü r = 13% = 0, 13 ü t = 2 év n = 24 hónap

Készítette: Papp József 3. 3. 5 feladat megoldása Egy év elteltével a tőketartozása:

Készítette: Papp József Teljes hiteldíj mutató - THM n A THM: - Teljes hiteldíj mutató – az a belső kamatláb, amely mellett a hitelfelvevő által visszafizetett tőke és hiteldíj egyenlő a hitelfelvevő által folyósításkor a pénzügyi intézménynek fizetett költségekkel csökkentett hitelösszeggel. (A THM jutalék, kezelési költség stb. fizetése esetén magasabb, mint a hitel kamatlába!)

Készítette: Papp József Teljes hiteldíj mutató - THM

Készítette: Papp József 3. 4. 1 feladat n A „Szerelek” Gépészmérnöki Kft. újonnan elvállalt tervező munkáinak ellátásához néhány számítógép vásárlása szükséges. A beszerzési ár 2. 000 Ft. A cég a beruházás finanszírozásához szükséges pénzösszeg felével rendelkezik, ezért a KB banktól 1. 000 Ft fejlesztési kölcsönt vesz fel. Az adósságot 1 év alatt, 2 azonos részletben kell megfizetni. A kamatláb évi 14%. A bank a hitel teljes összegének 2, 5%-át egyszeri kezelési költségként, 12. 500 Ft-ot hitelbírálati díjként és további 15. 000 Ftot hitelfolyósítási jutalékként számolja fel. Számítsa ki a Teljes Hiteldíj Mutatót!

Készítette: Papp József 3. 4. 1 feladat megoldása Határozzuk meg a rendelkezésre álló adatokat: ü H = 1. 000 Ft ü k = 14% = 0, 14 ü t = 1 év n = 2 félév ü Kezelési költség: 1. 000 ∙ 0, 025 = 25. 000 Ft ü Hitelbírálati díj: 12. 500 Ft ü Hitelfolyósítási díj: 15. 000 Ft

Készítette: Papp József 3. 4. 1 feladat megoldása Összes költség: 25. 000 + 12. 500 + 15. 000 = 52. 500 Ft A Teljes Hiteldíj Mutató :

Készítette: Papp József 3. 4. 1 feladat megoldása

Készítette: Papp József 3. 4. 1 feladat megoldása

Készítette: Papp József 3. 4. 2 feladat n Gépjármű vásárlás finanszírozására svájci frank alapú kölcsönt igényel egy kereskedelmi banktól. A bank által engedélyezett hitel összege 960. 000 Ft, amely egy összegben kerül folyósításra. A kölcsön frankban kerül meghatározásra, a törlesztés pedig azonos összegekben, a mindenkori aktuális árfolyamon történik. A kölcsön lejárata 48 hónap. Az első törlesztés az igénybevétel napját követő 1 hónap múlva esedékes. A frank aktuális eladási árfolyama 166, 54 HUF/CHF, a vételi árfolyama pedig 163, 28 HUF/CHF. A feltételezés szerint a hitel futamideje alatt a devizaárfolyamok nem változnak! Számítsa ki a havonta fizetendő törlesztő-részleteket, ha a bank évi 5% kamatot számít fel!

Készítette: Papp József 3. 4. 2 feladat megoldása Határozzuk meg a rendelkezésre álló adatokat: ü HHUF = 960. 000 Ft ü r = 5% = 0, 05 ü n = 48 hónap ü Eladási HUF/CHF: 166, 54 Ft ü Vételi HUF/CHF: 163, 28 Ft A magyar forintban folyósított kölcsön összegének megfelelő frank hitel összegét a bank deviza vételi árfolyamán kell kiszámítani!

Készítette: Papp József 3. 4. 2 feladat megoldása

Készítette: Papp József 3. 4. 3 feladat n Gépjármű vásárlás finanszírozására euró alapú kölcsönt igényel egy kereskedelmi banktól. A bank által engedélyezett hitel összege 1. 060. 000 Ft, amely egy összegben kerül folyósításra. A kölcsön euróban kerül meghatározásra, a törlesztés pedig azonos összegekben, a mindenkori aktuális árfolyamon történik. A kölcsön lejárata 48 hónap. Az első törlesztés az igénybevétel napját követő 1 hónap múlva esedékes. Az euró aktuális eladási árfolyama 256, 54 HUF/EUR, a vételi árfolyama pedig 253, 28 HUF/EUR. A hitelintézet évi 15% ügyleti kamatot számít fel. A feltételezés szerint a hitel futamideje alatt a devizaárfolyamok nem változnak! Számítsa ki a havonta fizetendő törlesztő-részleteket.

Készítette: Papp József 3. 4. 3 feladat megoldása Határozzuk meg a rendelkezésre álló adatokat: ü HHUF = 1. 060. 000 Ft ü r = 15% = 0, 15 ü n = 48 hónap ü Eladási HUF/EUR: 256, 54 Ft ü Vételi HUF/EUR: 253, 28 Ft A magyar forintban folyósított kölcsön összegének megfelelő euró hitel összegét a bank deviza vételi árfolyamán kell kiszámítani!

Készítette: Papp József 3. 4. 3 feladat megoldása