Historical Perspectives Stephen Kleene 1909 1994 Founded recursive

Historical Perspectives Stephen Kleene (1909 -1994) • Founded recursive function theory • Pioneered theoretical computer science • Student of Alonzo Church; was at the Institute for Advanced Study (1940) • Invented regular expressions • Kleene star / closure, Kleene algebra, Kleene recursion theorem, Kleene fixed point theorem, Kleene-Rosser paradox “Kleeneliness is next to Gödeliness”

Historical Perspectives Noam Chomsky (1928 -) • Linguist, philosopher, cognitive scientist, political activist, dissident, author • Father of modern liguistics • Pioneered formal languages • Developed generative grammars Invented context-free grammars • Defined the Chomsky hierarchy • Influenced cognitive psychology, philosophy of language and mind • Chomskyan linguistics, Chomskyan syntax, Chomskyan models • Critic of U. S. foreign policy • Most widely cited living scholar Eighth most-cited source overall!

“…I must admit to taking a copy of Noam Chomsky's ‘Syntactic Structures’ along with me on my honeymoon in 1961 … Here was a marvelous thing: a mathematical theory of language in which I could use as a computer programmer's intuition!” - Don Knuth on Chomsky’s influence

Formal Languages: Review Alphabet: a finite set of symbols S={a, b} String: a finite sequence of symbols ababbaab Language: a set of strings L={a, aaa, …} String length: number of symbols in it |aba|=3 String concatenation: w 1 w 2 ab • ba=abba Empty string: e or ^ "w w • e = e • w = w Language concatenation: {1, 2} • {a, aa, …} L 1 L 2={w 1 w 2 | w 1ÎL 1, w 2ÎL 2} ={1 a, 2 a, 1 aa, 2 aa, …} • String exponentiation: wk = ww…w (k times) a 3=aaa • Language exponentiation: Lk = LL…L (k times) {0, 1}32 LL = L 2 Lk=LLk-1 L 0={e} • •

Formal Languages: Review • String reversal: w. R (aabc)R=cbaa • Language reversal: LR ={w. R | wÎL} {ab, cd}R={ba, dc} • Kleene closure: L* = L 0 È L 1 È L 2 È L 3 È. . . {a}* L+ = L 1 È L 2 È L 3 È L 4 È. . . {a}+ Theorem: L+ = LL* • Trivial language: {e} • L=L • {e}=L • Empty language: Ø Ø*={e} • All finite strings: S* LÍS* "L {a, aa, …} • {1, 2} Theorem: S* is countable, |S*| = |Z| dovetailing * S Theorem: 2 is uncountable. diagonalization Theorem: S* contains no infinite strings in Si Theorem: (L*)* =L* L*Í(L*)* & (L*)*ÍL*

Finite Automata: Review Basic idea: a FA is a “machine” that changes states while processing symbols, one at a time. • Finite set of states: Q = {q 0, q 1, q 3, . . . , qk} • Transition function: d: Q´S ® Q q 1 qi • Initial state: q 0 Î Q q 0 • Final states: FÍQ qk qj • Finite automaton is M=(Q, S, d, q 0, F) Ex: an FA that accepts all odd-length strings of zeros: q 0 0 0 q 1 M=({q 0, q 1}, {0}, {((q 0, 0), q 1), ((q 1, 0), q 0)}, q 0, {q 1})

Finite Automata: Review FA operation: consume a string wÎS* one symbol at a time while changing states Acceptance: end up in a final state Rejection: anything else (including hang-up / crash) Ex: FA that accepts all strings of form abab…= (ab)* M q 0 a M=({q 0, q 1}, {a, b}, {((q 0, a), q 1), ((q 1, b), q 0)}, q 0, {q 0}) q 1 b b M’ q 2 a, b a But M “crashes” on input string “abba”! Solution: add dead-end state to fully specify M M’=({q 0, q 1, q 2}, {a, b}, {((q 0, a), q 1), ((q 1, b), q 0), ((q 0, b), q 2), ((q 1, b), q 2). ((q 2, a), q 2), ((q 2, b), q 2) }, q 0, {q 0})

Finite Automata: Review Transition function d extends from symbols to strings: d: Q´S*®Q d(q 0, wx) = d(d(q 0, w), x) where d(qi, e) = qi Language of M is L(M)={wÎS*| d(q 0, w) ÎF} Definition: a language is regular iff it is accepted by some FA. Theorem: Complementation preserves regularity. Proof: Invert final and non-final states in fully specified FA. a a q 0 M q 1 q 0 M’ q 1 b b b q 2 a, b a Wh com y ar ple e the * * me se L(M’)= b(a+b) + (a+b) a nts ? * * + (a+b) (aa+bb)(a+b) L(M)=(ab)* M’ “simulates” M and does the opposite!

Finite Automata: Review Theorem: Intersection perserves regularity. Proof: (“parallel” simulation): • Construct all super-states, one per each state pair. c u str ” n tio • New super-transition function jumps among n o c super-states, simulating old transition function t c u d • Initial super state contains both oldro initial states. p s • Final super states contains pairs of old final states. s o r c “ language as original • Resulting DFA accepts same NFA (but size can be the product of two old sizes). Given M 1=(Q 1, S, d 1, q’, F 1) and M 2=(Q 2, S, d 2 , q”, F 2) construct M=(Q, S, d, q, F) Q = Q 1´Q 2 F = F 1´F 2 q=(q’, q”) d : Q´S ® Q d((qi, qj), x) = (d 1(qi, x), d 2(qj, x))

Finite Automata: Review Theorem: Union preserves regularity. Proof: De Morgan's law: L 1 È L 2 = L 1 Ç L 2 Or cross-product construction, i. e. , parallel simulation with F = (F 1´Q 2) È (Q 1´F 2) Theorem: Set difference preserves regularity. Proof: Set identity L 1 – L 2 = L 1 Ç L 2 Or cross-product construction, i. e. , parallel simulation with F = (F 1´(Q 2 –F 2)) Theorem: XOR preserves regularity. Proof: Set identity L 1 Å L 2 = (L 1 È L 2) – (L 1 Ç L 2) Or cross-product construction, i. e. , parallel simulation with F = (F 1´(Q 2–F 2)) È ((Q 1–F 1)´F 2) Meta-Theorem: Identity-based proofs are easier!

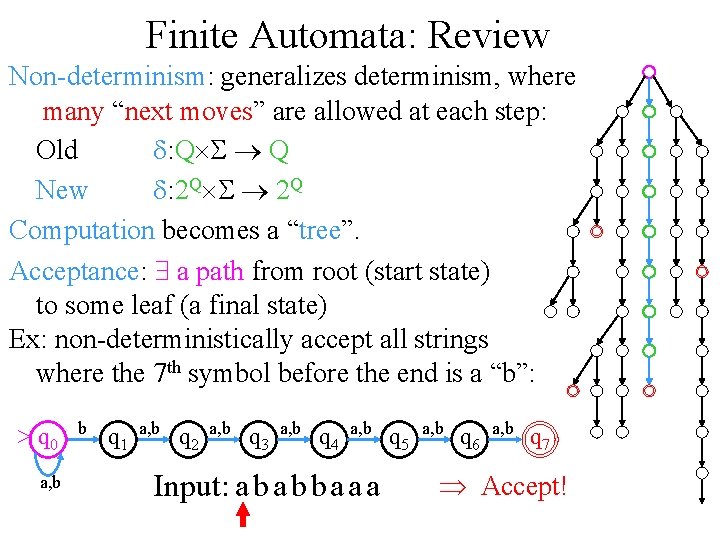
Finite Automata: Review Non-determinism: generalizes determinism, where many “next moves” are allowed at each step: Old d: Q´S ® Q New d: 2 Q´S ® 2 Q Computation becomes a “tree”. Acceptance: $ a path from root (start state) to some leaf (a final state) Ex: non-deterministically accept all strings where the 7 th symbol before the end is a “b”: q 0 a, b b q 1 a, b q 2 a, b q 3 a, b q 4 a, b Input: a b b a a a q 5 a, b q 6 a, b q 7 Þ Accept!

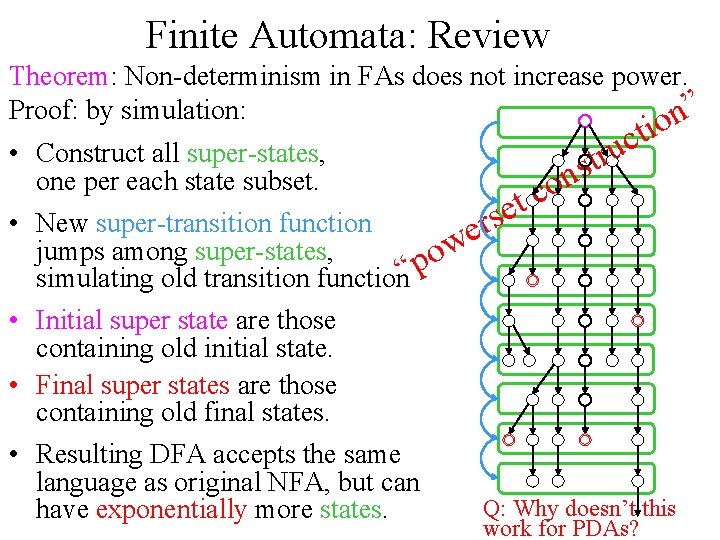
Finite Automata: Review Theorem: Non-determinism in FAs does not increase power. Proof: by simulation: n” o i t c u r • Construct all super-states, t s n one per each state subset. o c t e s • New super-transition function r e w jumps among super-states, o simulating old transition function“p • Initial super state are those containing old initial state. • Final super states are those containing old final states. • Resulting DFA accepts the same language as original NFA, but can Q: Why doesn’t this have exponentially more states. work for PDAs?

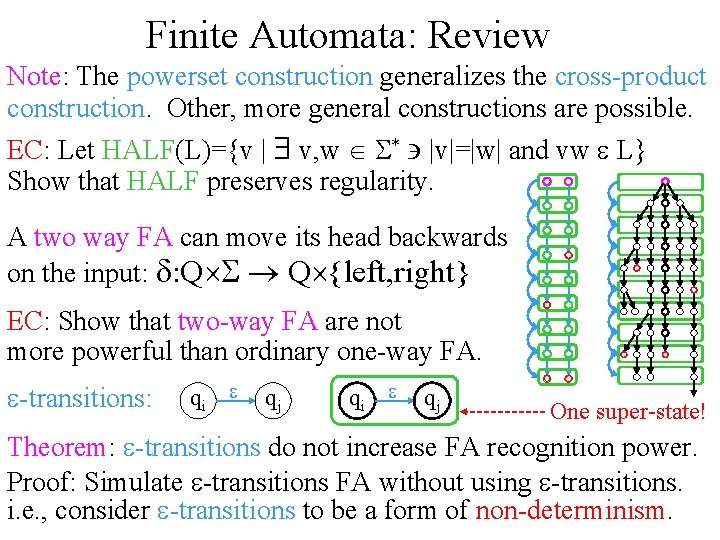
Finite Automata: Review Note: The powerset construction generalizes the cross-product construction. Other, more general constructions are possible. EC: Let HALF(L)={v | $ v, w Î S* ' |v|=|w| and vw e L} Show that HALF preserves regularity. A two way FA can move its head backwards on the input: d: Q´S ® Q´{left, right} EC: Show that two-way FA are not more powerful than ordinary one-way FA. e-transitions: qi e qj One super-state! Theorem: e-transitions do not increase FA recognition power. Proof: Simulate e-transitions FA without using e-transitions. i. e. , consider e-transitions to be a form of non-determinism.

The movie “Next” (2007) Based on the science fiction story “The Golden Man” by Philip Dick Premise: a man with the super power of non-determinism! At any given moment his reality branches into multiple directions, and he can choose the branch that he prefers! Transition function!

Regular Expressions: Review Regular expressions are defined recursively as follows: Ø empty set {e} trivial language q 0 {x} " xÎS singleton language q 0 x q 1 Inductively, if R and S are regular expressions, then so are: (R+S) RS R* union concatenation Kleene closure e e M 1 M 2 e e M 2 Compositions! e M e Examples: aa(a+b)*bb (a+b)*b(a+b)*a(a+b)* Theorem: Any regular expression is accepted by some FA.