Hilfe 1 ADDITION SUBTRAKTION Addition Von hinten nach
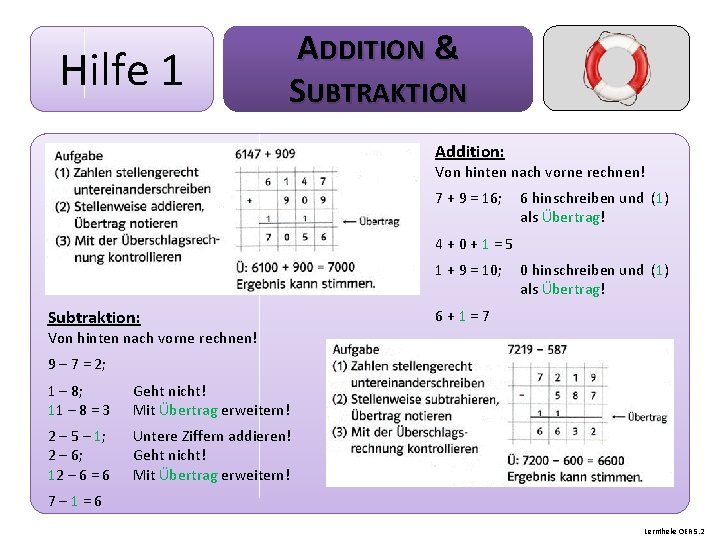
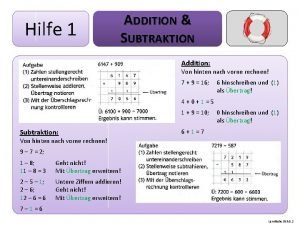
Hilfe 1 ADDITION & SUBTRAKTION Addition: Von hinten nach vorne rechnen! 7 + 9 = 16; 6 hinschreiben und (1) als Übertrag! 4 + 0 + 1 = 5 1 + 9 = 10; Subtraktion: 0 hinschreiben und (1) als Übertrag! 6 + 1 = 7 Von hinten nach vorne rechnen! 9 – 7 = 2; 1 – 8; 11 – 8 = 3 Geht nicht! Mit Übertrag erweitern! 2 – 5 – 1; 2 – 6; 12 – 6 = 6 Untere Ziffern addieren! Geht nicht! Mit Übertrag erweitern! 7 – 1 = 6 Lerntheke OER 5. 2
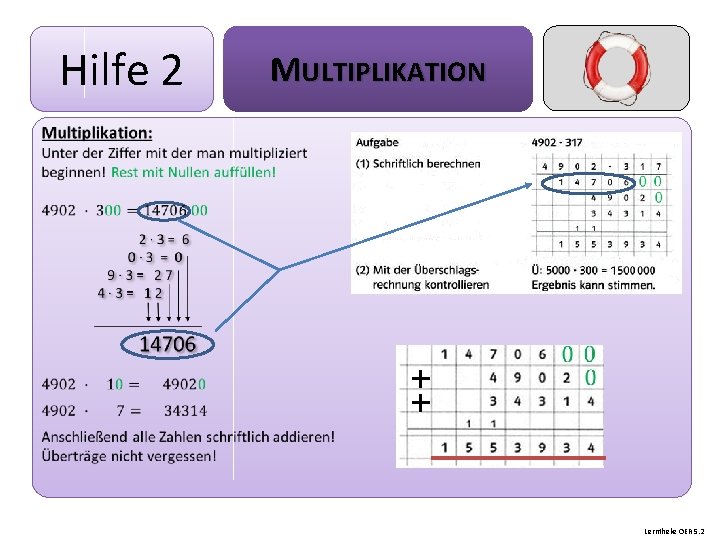
Hilfe 2 MULTIPLIKATION Lerntheke OER 5. 2

Hilfe 2 DIVISION Lerntheke OER 5. 2

Hilfe 3 RUNDEN Beim Runden von Zahlen betrachtet man die Ziffer rechts von der Stelle, auf die gerundet werden soll. Ist die Ziffer eine 0; 1; 2; 3; 4, dann wird abgerundet. Ist die Ziffer eine 5; 6; 7; 8; 9, dann wird aufgerundet. Beim Runden verwendet man das Zeichen ≈. Man sagt: „…ist etwa wie…“ oder „…ist ungefähr so viel wie…“ Beispiel: Runden auf Zehner: 230 231 232 233 234 235 236 237 238 239 ≈ 230 (abgerundet) ≈ 240 (aufgerundet) Lerntheke OER 5. 2
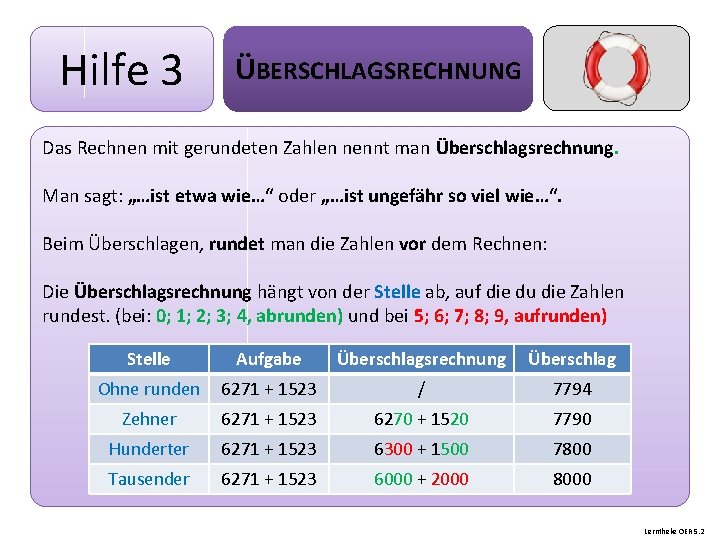
Hilfe 3 ÜBERSCHLAGSRECHNUNG Das Rechnen mit gerundeten Zahlen nennt man Überschlagsrechnung. Man sagt: „…ist etwa wie…“ oder „…ist ungefähr so viel wie…“. Beim Überschlagen, rundet man die Zahlen vor dem Rechnen: Die Überschlagsrechnung hängt von der Stelle ab, auf die du die Zahlen rundest. (bei: 0; 1; 2; 3; 4, abrunden) und bei 5; 6; 7; 8; 9, aufrunden) Stelle Aufgabe Überschlagsrechnung Überschlag Ohne runden 6271 + 1523 / 7794 Zehner 6271 + 1523 6270 + 1520 7790 Hunderter 6271 + 1523 6300 + 1500 7800 Tausender 6271 + 1523 6000 + 2000 8000 Lerntheke OER 5. 2
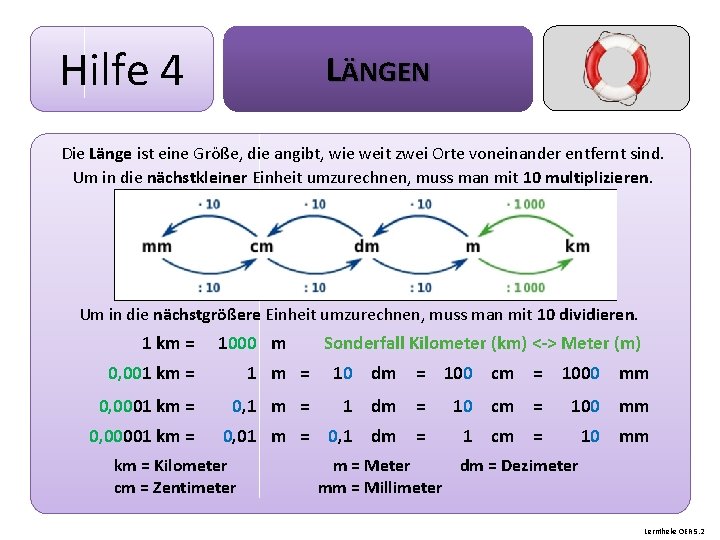
Hilfe 4 LÄNGEN Die Länge ist eine Größe, die angibt, wie weit zwei Orte voneinander entfernt sind. Um in die nächstkleiner Einheit umzurechnen, muss man mit 10 multiplizieren. Um in die nächstgrößere Einheit umzurechnen, muss man mit 10 dividieren. 1 km = 1000 m 0, 001 km = 1 m = 0, 0001 km = 0, 1 m = 0, 00001 km = Sonderfall Kilometer (km) <-> Meter (m) 10 dm = 100 cm = 1000 mm 1 dm = 10 cm = 100 mm 0, 01 m = 0, 1 dm = 1 cm = 10 mm km = Kilometer cm = Zentimeter m = Meter dm = Dezimeter mm = Millimeter Lerntheke OER 5. 2
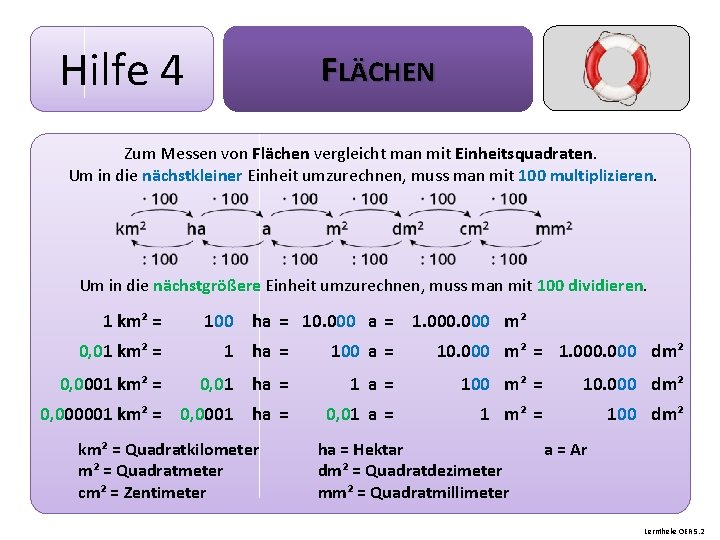
Hilfe 4 FLÄCHEN Zum Messen von Flächen vergleicht man mit Einheitsquadraten. Um in die nächstkleiner Einheit umzurechnen, muss man mit 100 multiplizieren. Um in die nächstgrößere Einheit umzurechnen, muss man mit 100 dividieren. 1 km² = 100 ha = 10. 000 a = 1. 000 m² 0, 01 km² = 1 ha = 100 a = 0, 0001 km² = 0, 01 ha = 1 a= 100 m² = 10. 000 dm² 0, 000001 km² = 0, 0001 ha = 0, 01 a = 1 m² = 100 dm² km² = Quadratkilometer m² = Quadratmeter cm² = Zentimeter 10. 000 m² = 1. 000 dm² ha = Hektar dm² = Quadratdezimeter mm² = Quadratmillimeter a = Ar Lerntheke OER 5. 2

Hilfe 5 GEWICHTE/ MASSE Das Gewicht ist eine Größe, die angibt, wie schwer etwas ist. Das Gewicht wird mit einer Waage gemessen. Um in die nächstgrößere Einheit umzurechnen, muss man mit 1000 dividieren. Um in die nächstkleiner Einheit umzurechnen, muss man mit 1000 multiplizieren. 1 t 0, 001 t = 1000 kg = 1000000 g = 100000 mg 1 kg = 1000000 mg 0, 0000001 t = 0, 001 kg = 1000 mg t = Tonnen kg = Kilogramm g = Gramm mg = Milligramm Lerntheke OER 5. 2
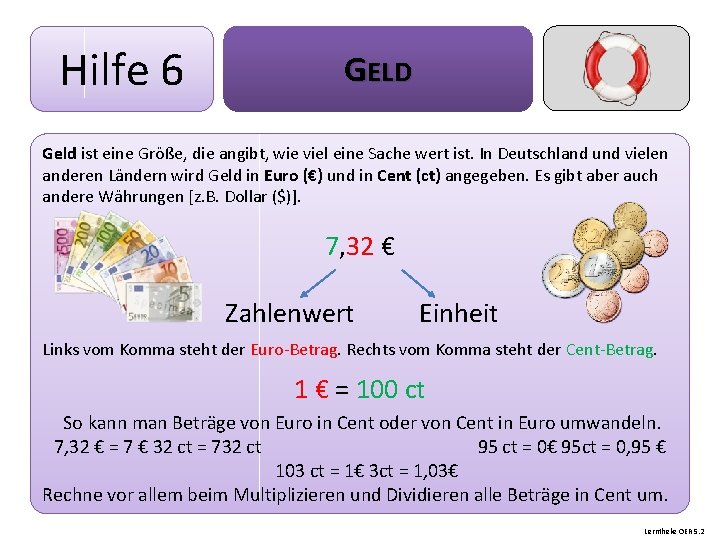
Hilfe 6 GELD Geld ist eine Größe, die angibt, wie viel eine Sache wert ist. In Deutschland und vielen anderen Ländern wird Geld in Euro (€) und in Cent (ct) angegeben. Es gibt aber auch andere Währungen [z. B. Dollar ($)]. 7, 32 € Zahlenwert Einheit Links vom Komma steht der Euro-Betrag. Rechts vom Komma steht der Cent-Betrag. 1 € = 100 ct So kann man Beträge von Euro in Cent oder von Cent in Euro umwandeln. 7, 32 € = 7 € 32 ct = 732 ct 95 ct = 0€ 95 ct = 0, 95 € 103 ct = 1€ 3 ct = 1, 03€ Rechne vor allem beim Multiplizieren und Dividieren alle Beträge in Cent um. Lerntheke OER 5. 2

Hilfe 6 GELD ÜBERSCHLAGEN Im Alltag muss man oft Kosten abschätzen. Zum Beispiel, wenn man einkauft und nicht genau weiß, ob man genug Geld dabei hat! Wenn es schnell gehen soll, kann man eine Überschlagsrechnung durchführen. Beispiel: Dazu schaut man sich die 1. Nachkommastelle an. Aufrunden bei 0 -4 Abrunden bei 5 -9 statt: rechne: 5, 10€ + 12, 98€ + 7, 90€ 5€ + 13€ + 8€ = 26€ also: 5, 10€ + 12, 98€ + 7, 90€ 26€ Lerntheke: Wiederholung und Vorbereitung - 5

Hilfe 7 ADDIEREN UND SUBTRAHIEREN MIT KOMMA Das Rechnen mit Kommazahlen ist gar nicht so schwer, wenn man weiß worauf man achten muss. Bei Kommazahlen handelt es sich um Dezimalzahlen. Die Zahl vor dem Komma ist eine ganze Zahl, die Zahl hinter dem Komma ist nur ein Teil vom Ganzen. 4, 25 sind also 4 Ganze und 0, 25 ist ein Teil vom Ganzen! Das Addieren und Subtrahieren mit Kommazahlen funktioniert genauso wie das Rechnen ohne Komma. Es gibt nur eine wichtige Regel: Komma unter Komma Lerntheke: Wiederholung und Vorbereitung - 5

Hilfe 8 ZEIT Ein Zeitpunkt ist ein genau festgelegter Termin, z. B. der 13. Juli oder 11: 30 Uhr. Eine Zeitspanne ist die Dauer zwischen zwei Zeitpunkten, z. B. eine Stunde, ein Jahr oder von 15 Uhr bis 18 Uhr. Zeitpunkt Zeitspanne Die Sendung beginnt um 17: 15 Uhr. Die Sendung dauert 45 Minuten. Die Schule hört um 15: 00 Uhr auf. In der Schule verbringen wir 7 Stunden. So kann man Einheiten der Zeit in andere Einheiten umrechnen: Zum ablesen einer Uhr, muss man folgendes Wissen: Viertelstunde = 15 Min. ; Halbestunde = 30 Min. ; Dreiviertelstunde = 45 Min. Lerntheke: Wiederholung und Vorbereitung - 5

Hilfe 9 MAßEINHEITEN Erklärung: Eine Größe wird in einer Maßeinheit mit einem festen Wert angegeben. Die Maßeinheiten sind noch einmal so unterteilt, damit man besonders große und besonders niedrige Größen verständlich ausdrücken kann. länger, größer, schwerer, mehr Zeit: 60 Sekunden = 1 Minute, 60 Minuten = 1 Stunde, 24 Stunden = 1 Tag, 7 Tage = 1 Woche, 4 Wochen = 1 Monat, 12 Monate = 1 Jahr Länge: 10 Millimeter = 1 Zentimeter, 10 Zentimeter = 1 Dezimeter, 10 Dezimeter = 1 Meter, 1000 Meter = 1 Kilometer Gewicht: 1000 Milligramm = 1 Gramm, 1000 Gramm = 1 Kilogramm, 1000 Kilogramm = 1 Tonne Geld: 100 Cent = 1 Euro Lerntheke: Wiederholung und Vorbereitung - 5
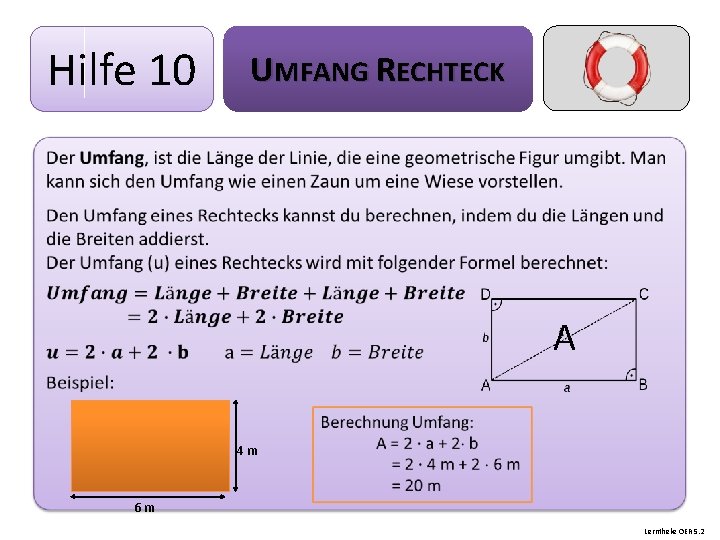
Hilfe 10 UMFANG RECHTECK A 4 m 6 m Lerntheke OER 5. 2
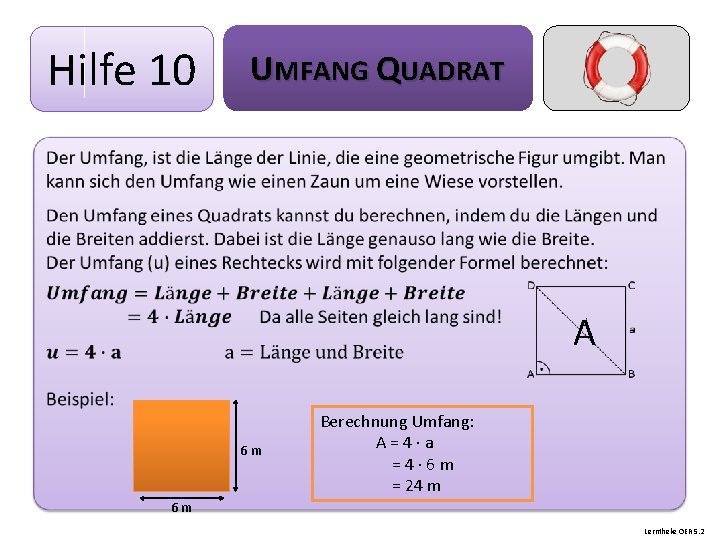
Hilfe 10 UMFANG QUADRAT A 6 m Berechnung Umfang: A = 4 a = 4 6 m = 24 m 6 m Lerntheke OER 5. 2

FLÄCHENINHALT RECHTECK Hilfe 11 A 4 m Berechnung Flächeninhalt: A = a b = 4 m 6 m = 24 m² 6 m Lerntheke OER 5. 2
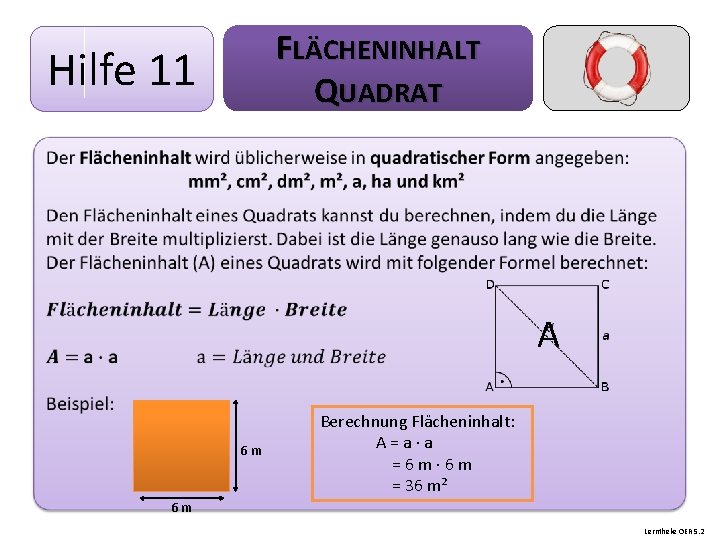
FLÄCHENINHALT QUADRAT Hilfe 11 A 6 m Berechnung Flächeninhalt: A = a a = 6 m = 36 m² 6 m Lerntheke OER 5. 2

Station 1 RECHNEN MIT GELD 1. ) Beim Einkaufen muss man genau aufpassen, da manche Preise nur in Cent angegeben werden. Schreibe in Euro und Cent. Beispiel: 134 ct = 1 € 34 ct = 1, 34 € a) 257 ct = ______ c) 33, 90 € = ______ b) 8361 ct = ______ d) 765, 49 € = ______ 6 4. ) Im Alltag muss man oft Kosten abschätzen. Wen es schnell gehen soll, kann man eine Überschlagsrechnung durchführen. Überschlage und runde auf ganze Euro. a) 2, 98€ + 17, 05€ + 4, 95€ _______ b) 14, 90€ - 6, 10 € - 2, 95€ _______ c) 23, 89€ - 8, 90€ + 3, 99€ _______ Lerntheke OER 5. 2

Station 1 LÖSUNG 1. ) Schreibe in Euro und Cent. Beispiel: 134 ct = 1 € 34 ct = 1, 34 € a) 257 ct = 2 € 57 ct = 2, 57 € c) 33, 90 € = 33€ 90 ct = 33, 90 € b) 8361 ct = 83 € 61 ct = 83, 61 € d) 765, 49 € = 765 € 49 ct = 76549 ct 4. ) Überschlage und runde auf ganze Euro. a) 2, 98€ + 17, 05€ + 4, 95€ 3€ + 17€ + 5€ = 25€ b) 14, 90€ - 6, 10 € - 2, 95€ 15€ - 6€ - 3€ = 6€ c) 23, 89€ - 8, 90€ + 3, 99€ 24€ - 9€ + 4€ = 19€ Lerntheke OER 5. 2

Station 2 RECHNEN MIT GELD 1 Metzgerei Dimpfelmo -------ser ----------------Pute--n-s-c-h-n itz Rotwurst kg 2. 20 € kg 6 7 el 6. 90 € !!So ! ! e t o b e nderang Schweinefilet Fleischwur st kg 4. 30 € kg 11. 50 € Lerntheke OER 5. 2

Station 2 LÖSUNG 50, 00 € 4, 30 € + 4, 30 € 8, 60 € 2, 20 € - 2, 20 € + 6, 90 € - 6, 90 € + 8, 60 € - 8, 60 € + 11, 50 € - 11, 50 € 1 2 29, 20 € 50, 00 € - 29, 20 € 1 1 20, 80 € 4, 30 € + 4, 30 € 8, 60 € 2 3 20, 80 € Lerntheke OER 5. 2

Station 3 RECHNEN MIT GELD 1 1) Pierre muss beim Tierarzt für seine Katze 26, 85€ bezahlen. Er bezahlt mit zwei 20 Euro-Scheinen. Was bekommt er zurück? 2 2) Jana kauft sich fünf Hefte zu je 65 Cent und drei Bleistifte zu je 55 Cent. Wie viel bekommt sie zurück, wenn sie mit einem 10 -Euro-Schein bezahlt? 3) Bernd will Süßigkeiten kaufen. Ein Schokoriegel kostet 45 Cent. Ein Dreier-Pack kostet 1, 26€. a) Um wie viel Cent ist ein Dreierpack billiger? b) Bernd hat es sich nun doch anders überlegt. Er hat 5 Euro und 44 Cent dabei und kauft damit lieber eine Zahnbürste für 1, 74 € und Zahnpasta für 94 Cent. Den Rest steckt er zu Hause in sein Sparschwein. Wie viel ist das? 6 7 Lerntheke OER 5. 1
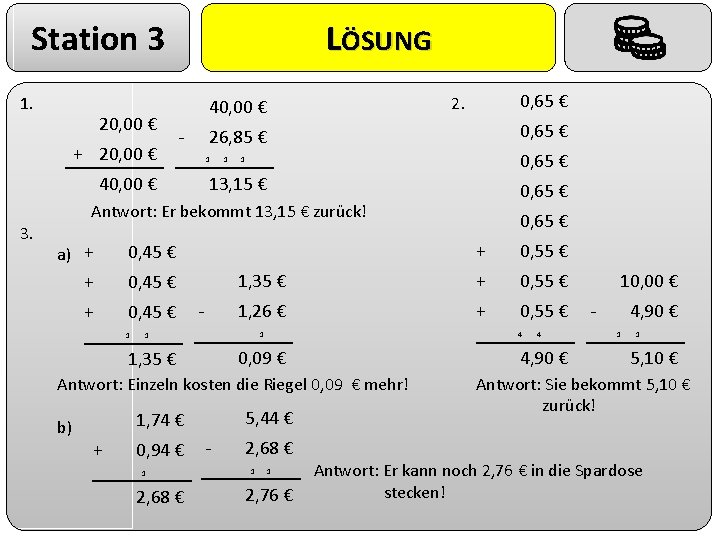
Station 3 1. 20, 00 € + 20, 00 € LÖSUNG - 40, 00 € 3. 0, 65 € 2. 40, 00 € 0, 65 € 26, 85 € 1 1 0, 65 € 1 13, 15 € 0, 65 € Antwort: Er bekommt 13, 15 € zurück! a) + 0, 45 € + 0, 45 € 1 - + 0, 55 € 1, 35 € + 0, 55 € 1, 26 € + 0, 55 € 1 1 4 0, 09 € 1, 35 € Antwort: Einzeln kosten die Riegel 0, 09 € mehr! b) 5, 44 € 1, 74 € + 0, 94 € 1 2, 68 € 0, 65 € - 4 4, 90 € 10, 00 € - 4, 90 € 1 1 5, 10 € Antwort: Sie bekommt 5, 10 € zurück! 2, 68 € Antwort: Er kann noch 2, 76 € in die Spardose stecken! 2, 76 € 1 1

Station 4 LÄNGENANGABEN UMWANDELN 1. Schreibe in der angegebenen Maßeinheit. Beispiel: 3 m 40 cm = 340 cm a) 7 m 85 cm = c) 3 dm 4 mm = 1 b) 30 cm 4 mm = d) 7 km 84 m = 2 4 2. Merke: Erst in die kleiner Einheit umrechnen, dann ausrechnen! Beispiel: 9 m + 30 cm = 900 cm + 30 cm = 930 cm a) 4 cm + 3 mm = b) 12 km + 40 m = c) 3 m + 50 mm = d) 45 dm + 22 mm = e) 2000 mm – 5 dm = 3. Wandle nun alle Ergebnisse aus Aufgabe 2. in die größere Einheit um. Lerntheke OER 5. 5

Station 4 LÖSUNG 1. Schreibe in der angegebenen Maßeinheit. Beispiel: 3 m 40 cm = 340 cm a) 7 m 85 cm = 785 cm c) 3 dm 4 mm = 304 dm b) 30 cm 4 mm = 304 mm d) 7 km 84 m = 7084 m 2. Merke: Erst in die kleiner Einheit umrechnen, dann ausrechnen! Beispiel: 9 m + 30 cm = 900 cm + 30 cm = 930 cm a) 4 cm + 3 mm = 40 mm + 3 mm = 43 mm b) 12 km + 40 m = 12000 m + 40 m = 12040 m c) 3 m + 50 mm = 3000 mm + 50 mm = 3050 mm d) 45 dm + 22 mm = 4500 mm + 22 mm = 4522 mm e) 2000 mm – 5 dm = 2000 – 500 mm = 1500 mm 3. Wandle nun alle Ergebnisse aus Aufgabe 2. in die größere Einheit um. a) b) c) d) e) 4, 3 cm 12, 04 km 3, 05 m 45, 22 dm 15 dm Lerntheke OER 5. 2

Station 5 LÄNGENANGABEN UMWANDELN Achtung, Kommaschreibweise! Gib die Länge in unterschiedlichen Schreibweisen an. 1 1. Beispiel: 4, 25 m = 4 m 25 cm = 4 m 2 dm 5 cm 2 a) 3, 5 cm b) 13, 24 m c) 3, 02 m d) 5, 070 km 4 2. Schreibe mit Komma 7 a) 5 km 555 m b) 4 m 4 cm c) 7 cm 4 mm d) 33 km 4 m 3. Petra liebt es, aus Wolle Armbänder zu flechten. Für ein Armband benötigt sie drei Fäden mit je 25 cm Länge. Sie hat ein Wollknäuel mit 50 m. a) b) c) Wie viel Wolle verbraucht Petra für ein Armband? Wie viele Armbänder kann sie aus dem Wollknäuel herstellen? Wie lang ist der Rest, der übrig bleibt? Lerntheke OER 5. 5

Station 5 LÖSUNG Lerntheke OER 5. 2

Station 6 RECHNEN MIT LÄNGEN Addieren und Subtrahieren von Längen a) Längenangaben mit unterschiedlichen Einheiten wandelt man zunächst in die kleinste Einheit um. Dann wird schriftlich addiert bzw. subtrahiert. b) 3 m 40 cm + 254 cm = 340 cm + 254 cm Längenangaben in der Kommaschreibweise schreibt man so untereinander, dass stets Komma unter Komma steht. Dann wird spaltenweise addiert bzw. subtrahiert. 3, 567 km + 0, 421 km _____ 3, 988 km 340 cm + 254 cm _____ 594 cm 1. Berechne. Wandle zuerst um. 2. Berechne. a) b) c) d) e) f) g) a) b) c) d) e) f) 15 cm + 5 mm = 35 cm + 350 mm = 2 m + 35 mm = 766 m – 4500 cm = 37 km – 95 dm = 5 km – 800 m - 1250 m = 3 m + 30 cm + 5 m + 85 cm = 1 4 7 9, 9 m + 9, 9 m = 2, 4 cm + 12, 8 m = 12, 5 cm – 7, 4 cm = 18, 26 km + 39, 58 km = 7, 34 km + 2, 18 km = 143, 7 cm – 56, 6 cm = Lerntheke OER 5. 5

Station 6 LÖSUNG 1. Berechne. Wandle zuerst um. a) 150 mm + 5 mm = 155 mm b) 350 mm + 350 mm = 700 mm c) 2000 mm + 35 mm = 2035 mm d) 76600 cm – 4500 cm = 72100 cm e) 370000 dm – 95 dm = 369905 dm f) 5000 m – 800 m – 1250 m = 2950 m g) 300 cm + 30 cm + 500 cm + 85 cm = 915 cm 2. Berechne. a) b) c) d) e) f) 19, 8 m 15, 2 m 5, 1 cm 57, 84 km 9, 52 km 87, 1 cm Lerntheke OER 5. 2
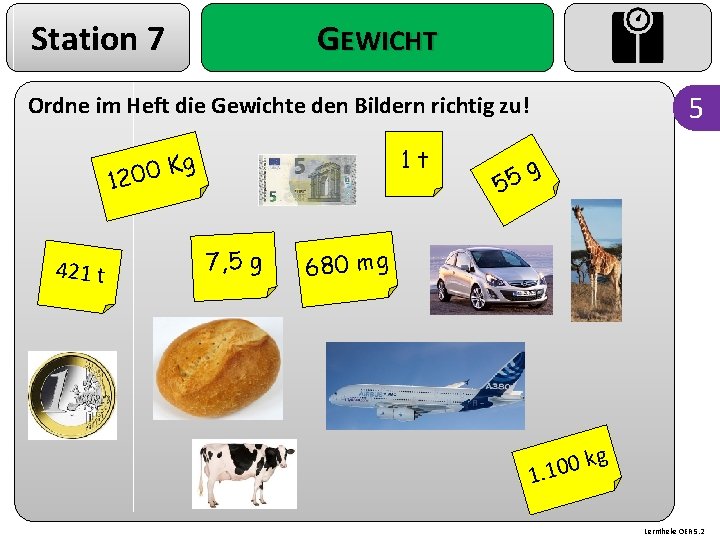
Station 7 GEWICHT 5 Ordne im Heft die Gewichte den Bildern richtig zu! 1 t g K 0 0 12 421 t 7, 5 g g 5 5 680 mg g k 0 0 1 1. Lerntheke OER 5. 2
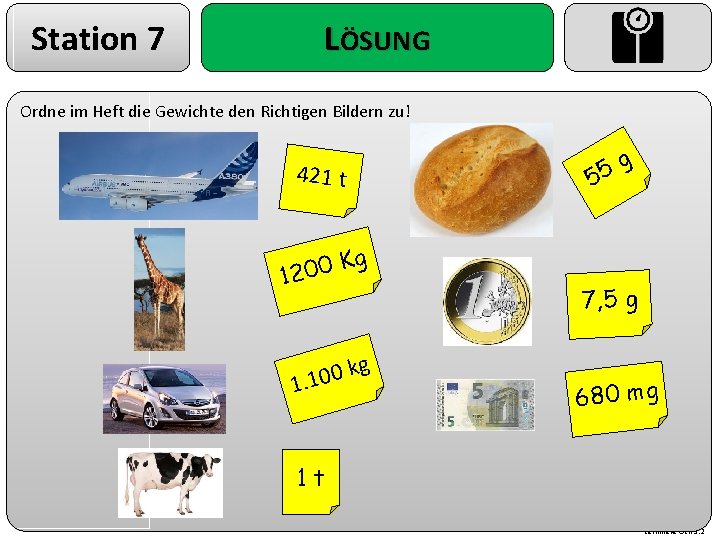
Station 7 LÖSUNG Ordne im Heft die Gewichte den Richtigen Bildern zu! g 5 5 421 t g K 0 0 2 1 7, 5 g g k 0 0 1. 1 680 mg 1 t Lerntheke OER 5. 2
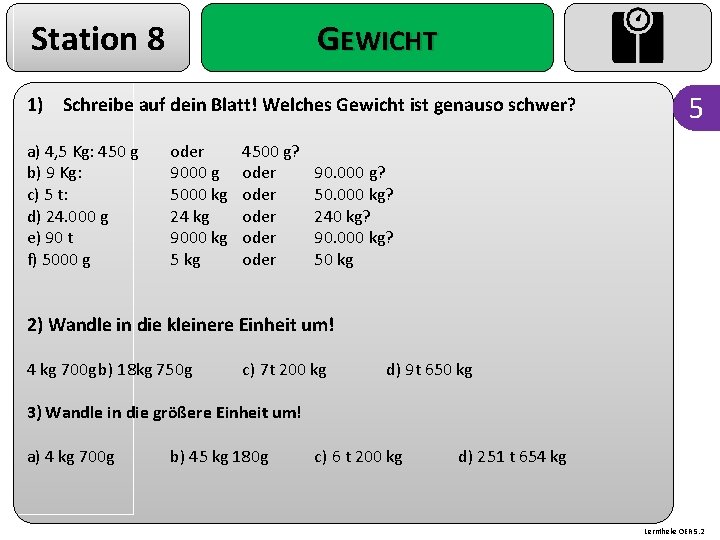
Station 8 GEWICHT 1) Schreibe auf dein Blatt! Welches Gewicht ist genauso schwer? a) 4, 5 Kg: 450 g b) 9 Kg: c) 5 t: d) 24. 000 g e) 90 t f) 5000 g oder 9000 g 5000 kg 24 kg 9000 kg 5 kg 4500 g? oder oder 5 90. 000 g? 50. 000 kg? 240 kg? 90. 000 kg? 50 kg 2) Wandle in die kleinere Einheit um! 4 kg 700 g b) 18 kg 750 g c) 7 t 200 kg d) 9 t 650 kg 3) Wandle in die größere Einheit um! a) 4 kg 700 g b) 45 kg 180 g c) 6 t 200 kg d) 251 t 654 kg Lerntheke OER 5. 2

Station 8 LÖSUNG 1) Schreibe auf dein Blatt! Welches Gewicht ist genauso schwer? a) 4, 5 Kg: 4500 g b) 9 Kg: c) 5 t: d) 24. 000 g e) 90 t f) 5000 g 9000 g 5000 kg 24 kg 90. 000 kg 5 kg 2) Wandle in die kleinere Einheit um! a) 4 kg 700 g = 4700 g c) 7 t 200 kg = 7200 kg b) 18 kg 750 g = 18. 750 g d) 9 t 650 kg = 9650 kg 3) Wandle in die größere Einheit um! a) 4 kg 700 g = 4, 7 kg c) 6 t 200 kg = 6, 2 t b) 45 kg 180 g = 45, 18 kg d) 251 t 654 kg = 251, 654 t Lerntheke OER 5. 2

Station 9 Am Flughafen Lea und Tim packen ihren Urlaubskoffer. Ihr Koffer darf am Flughafen maximal 20 kg schwer sein, da sie sonst für Übergewicht zuzahlen müssen. Ihren 1 5 gepackten Koffer stellen sie auf eine Personenwaage: „So ist der Koffer zu schwer“. Nun wiegen die beiden alle Sachen aus und müssen einige Dinge zurücklassen. Lea notiert ihre Angaben in Kilogramm, Tim hingegen in Gramm. - Koffer 2, 3 Kg - Tims Kleidung 5, 1 Kg Leas Kleidung 6, 2 Kg - Bücher 2400 g Geschenke 1700 g - Spielsachen 2100 g Getränke 1, 25 Kg Welche Gegenstände sollten zu Hause bleiben? Wie schwer ist ihr Koffer dann? Lerntheke OER 6. 2 …

Station 9 Gegeben: Maximalgewicht des Koffers: 20 Kg Gegenstände im Koffer: LÖSUNG - Koffer 2, 3 Kg - Tims Kleidung 5, 1 Kg Leas Kleidung 6, 2 Kg - Bücher 2400 g Geschenke 1700 g - Spielsachen 2100 g Getränke 1, 25 Kg Gesucht: - Gewicht des aktuellen Koffers. - Gegenstände, die nicht mitgenommen werden können und das daraus resultierende neue Gewicht des Koffers. Rechnung: 1700 g = 1, 7 kg; 2400 g = 2, 4 kg 2100 g = 2, 1 Kg 2, 3 Kg + 6, 2 Kg + 1, 7 Kg + 1, 25 Kg + 5, 1 Kg + 2, 4 Kg + 2, 1 Kg = 20, 95 Kg – 1, 25 Kg = 19, 7 Kg Antwort: Wenn Lea und Tim die Getränke aus dem Koffer nehmen, ist das Gewicht unter 20 Kg. Insgesamt hat der Koffer dann ein Gewicht von 19, 7 Kg. Vielleicht haben die beiden Glück und dürfen trotzdem alles mitnehmen, weil einige Fluggesellschaften eine Kulanz von 1 -2 Kg gewähren. Lerntheke OER 6. 2

Station 10 Tafel Schokolade Welche Nährwerte hat ein Stück Schokolade? 1 2 5 a) Lies die Nährwerte (Kohlenhydrate, Fette, Eiweiße, Kalorien) für 100 g ab und übertrage diese in einer Tabelle in dein Arbeitsheft. b) Berechne nun wieviel Kohlenhydrate, Fett, Eiweiß und Kalorien einzelnes Stück Schokolade enthält. c) Lies hinten auf der Schokoladen Tafel ab, wie viel Gramm Zucker in einer Tafel stecken. Wie viele Zuckerwürfel stecken in der Tafel, wenn 1 Zuckerwürfel ca. 3 g wiegt? Lerntheke OER 6. 2 …

Station 10 LÖSUNG c) b) Nährstoff: Pro 100 g Kohlehydrate: 58, 5 g Eiweiße: 6, 5 g Fett: 29, 5 g Aus dem Bild kann man entnehmen, dass eine Tafel 24 Stückchen hat. Man muss also jede Nährwertangabe (Kohlenhydrate, Eiweiße, Fett) und die Kalorien durch 24 teilen, dadurch weiß man die Werte für 1 Stück. Kalorien: 530 kcal d) Eine Tafel mit 100 g hat insgesamt 58 g Zucker. Bei dieser Aufgabe muss man einfach die 57, 5 g durch die 3 g teilen, weil ja 1 Zuckerwürfel ca. 3 g wiegt. Nährstoff: Pro Stück: Kohlehydrate: 2, 4 g Eiweiße: 0, 3 g Fett: 1, 2 g Kalorien: 22 kcal Ergebnis: ca. 20 Zuckerwürfel. Wenn man überlegt wie klein eigentlich so eine Tafel ist, dann ist das schon ne Menge. Lerntheke OER 6. 2

Station 11 UHREN LESEN Schau dir die Uhren rechts im Bild an. Beachte, ob die Uhrzeit am Tag oder in der Nacht anzeigt! a) Wie spät ist es jeweils in I. Einer Viertelstunde, II. einer halben Stunde, III. einer Dreiviertelstunde? b) Wie spät war es jeweils vor I. einer Viertelstunde, II. einer halben Stunde, III. einer Dreiviertelstunde? Schreibe für jede Uhr einzeln auf: 1. Uhr: a) 13: 15 Uhr, 13: 30 Uhr, … b) 12: 45 Uhr, … 1) Tag 8 2) Nacht 3) Tag 4) Nacht Lerntheke OER 5. 2

Station 11 LÖSUNGEN a) 1. Uhr: 13. 15 Uhr, 13. 30 Uhr, 13. 45 Uhr 2. Uhr: 4. 45 Uhr, 5. 15 Uhr 3. Uhr: 17. 30 Uhr, 17. 45 Uhr, 18 Uhr 4. Uhr: 4 Uhr, 4. 15 Uhr, 4. 30 Uhr b) 1. Uhr: 12. 45 Uhr, 12. 30 Uhr, 12. 15 Uhr 2. Uhr: 4. 15 Uhr, 4 Uhr, 3. 45 Uhr 3. Uhr: 17 Uhr, 16. 45 Uhr, 16. 30 Uhr 4. Uhr: 3. 30 Uhr, 3. 15 Uhr, 3 Uhr

Station 12 MAßEINHEITEN 1/2 4 Wahr oder falsch? a) b) c) d) e) f) g) h) i) j) k) l) 5 Stunden dauern länger als 320 Minuten! 150 Monate dauern länger als 13 Jahre! 130 Euro sind weniger als 10. 000 Cent! 10. 000 Zentimeter sind mehr als 100 Dezimeter! 3 Jahre dauern länger als 32 Monate! 14 Tonnen sind schwerer als 1500 Kilogramm! 1000 Millimeter sind kürzer als 10 Zentimeter! 15 Euro sind mehr als 950 Cent! 500 Sekunden dauern länger als 10 Minuten! 900 Kilogramm sind weniger als eine Tonne! 4000 Gramm sind leichter als 3 Kilogramm! 5 Tage dauern länger als 100 Stunden! 5 6 8 9 Lerntheke: Wiederholung und Vorbereitung - 5

Station 12 LÖSUNG 1/2 Wahr oder falsch? a) b) c) d) e) f) g) h) i) j) k) l) 5 Stunden dauern länger als 320 Minuten! 150 Monate dauern länger als 13 Jahre! 130 Euro sind weniger als 10. 000 Cent! 10. 000 Zentimeter sind mehr als 100 Dezimeter! 3 Jahre dauern länger als 32 Monate! 14 Tonnen sind schwerer als 1500 Kilogramm! 1000 Millimeter sind kürzer als 10 Zentimeter! 15 Euro sind mehr als 950 Cent! 500 Sekunden dauern länger als 10 Minuten! 900 Kilogramm sind weniger als eine Tonne! 4000 Gramm sind leichter als 3 Kilogramm! 5 Tage dauern länger als 100 Stunden! Falsch Wahr Falsch Wahr Lerntheke: Wiederholung und Vorbereitung - 5

Station 12 MAßEINHEITEN 2/2 Wie viel. . . ? ? ? a) b) c) d) e) f) g) h) i) j) k) l) Wie viele Minuten sind 7 Stunden? Wie viele Meter sind 712 Zentimeter Wie viele Gramm sind 20 Kilogramm. Wie viele Euro sind 8723 Cent? Wie viele Dezimeter sind 23 Kilometer? Wie viele Monate sind 12 Jahre? Wie viele Tonnen sind 3000 Kilogramm? Wie viele Sekunden sind 2 Tage? Wie viele Cent sind 15 Euro? Wie viele Millimeter sind 3 Meter? Wie viele Jahre sind 48 Monate? Wie viele Zentimeter sind 3 Dezimeter? 4 5 6 8 9 Lerntheke: Wiederholung und Vorbereitung - 5

Station 12 LÖSUNG 2/2 Wie viel. . . ? ? ? a) 24, 98€ a) b) b) c) c) d) d) e) f) e) g) h) f) i) g) j) k) l) Wie viele Minuten sind 7 Stunden? 420 Minuten 5, 85€ Wie viele Meter sind 712 Zentimeter 7, 12 Meter Wie viele Gramm sind 20 Kilogramm. 20. 000 Gramm 18, 98€ Wie viele Euro sind 8723 Cent? 87, 23 Euro 20€ Wie viele Dezimeter sind 23 Kilometer? 230000 Meter Wie viele Monate sind 12 Jahre? 144 Monate 11€ Wie viele Tonnen sind 3000 Kilogramm? 3 Tonnen Wie viele Sekunden sind 2 Tage? 172. 800 Sekunden 20€ Wie viele Cent sind 15 Euro? 1500 Cent 1€ Wie viele Millimeter sind 3 Meter? 3000 Millimeter Wie viele Jahre sind 48 Monate? 4 Jahre Wie viele Zentimeter sind 3 Dezimeter? 30 Zentimeter Lerntheke: Wiederholung und Vorbereitung - 5

Station 13 ZEITANGABEN 1. Vergleiche und setze > oder < ein. Beispiel: 245 min > 4 h a) 90 s � 1 min c) 50 h � 2 d e) 2000 s � ½h 8 b) 20 min � ¼h d) 240 h � 24 d 2. Amélies Unterricht beginnt um 7. 50 Uhr. Alle Unterrichtsstunden dauern 45 Minuten. Zwischen der dritten und vierten Stunde sind 15 Minuten Pause, sonst 5 Minuten. a) Wann beginnt die zweite Stunde? b) Wann endet die 15 -Minuten-Pause? c) Um welche Uhrzeit ist die 6. Stunde beendet? Lerntheke OER 5. 2

Station 13 1. Vergleiche und setze > oder < ein. Beispiel: 245 min > 4 h a) 90 s > 1 min c) 50 h > 2 d e) 2000 s > ½h LÖSUNG b) 20 min > ¼h d) 240 h < 24 d 2. Amélies Unterricht beginnt um 7. 50 Uhr. Alle Unterrichtsstunden dauern 45 Minuten. Zwischen der dritten und vierten Stunde sind 15 Minuten Pause, sonst 5 Minuten. a) Wann beginnt die zweite Stunde? (um 8. 40 Uhr) b) Wann endet die 15 -Minuten-Pause? (um 10. 30 Uhr) c) Um welche Uhrzeit ist die 6. Stunde beendet? (um 12. 55 Uhr)

Station 14 UMFANG RECHTECK 1. Aufgabe: Zeichne die Rechtecke mit den angegebenen Seitenlängen auf ein weißes Blatt Papier. u 10 Beispiel 3 cm 4 cm 1. 2. 3. 4. 5. Länge 5 cm 8 cm 12 cm 5, 5 cm 4, 3 cm Breite 3 cm 4 cm 7 cm 3, 5 cm 3. Aufgabe: Ein Freibad wird neu errichtet. Um den Garten herum soll jetzt noch ein Zaun gebaut werden, damit keine fremden auf das Grundstück können. Wie viel Meter Zaun benötigt man? 2, 2 cm Lerntheke OER 5. 2

Station 14 Aufgabe 1: Lösungen zu Aufgabe 1 findet ihr auf der Folie zu Station 15. Ihr müsst die Folie auf die Rechtecke legen, um zu sehen, ob ihr die Rechtecke in der richtigen Größe gezeichnet habt. Aufgabe 3: Länge = 15 m Breite = 30 m u LÖSUNG Aufgabe 2 1. 2. 3. 4. 5. Länge 5 cm 8 cm 12 cm 5, 5 cm 4, 3 cm Breite 3 cm 4 cm 7 cm 3, 5 cm 2, 2 cm Umfang 16 cm 24 cm 38 cm 13 cm Antwort: Es wird ein Zaun von 90 m Länge benötigt.

Station 15 a) b) c) d) e) u UMFANG RECHTECK &QUADRAT Aufgabe 2: Berechne die fehlenden Größen im Heft. Seitenlänge a = 6 cm Seitenlänge a = 4, 5 cm Seitenlänge a = 2 cm Seitenlänge a = 12 mm Seitenlänge a = 1, 5 dm 4 Seite a Seite b a) 15 cm 13 cm e) 5, 4 cm b) 30 dm 5 dm f) 4 dm c) 3 dm 45 dm g) 13 mm d) 2, 5 km 1, 4 km h) 2, 6 km Seite a 9 10 Aufgabe 3: Miss die Seiten und berechne den Umfang. Lerntheke OER 5. 2

Station 15 Aufgabe 1: Aufgabe 2: Aufgabe 3: u LÖSUNG

Station 16 UMFANG RECHTECK &QUADRAT Aufgabe 1: Im Chemieraum sind die Umrandungen der Tische kaputt und müssen erneuert werden. Ein Tisch ist 2, 8 m lang und 0, 6 m breit. Wie lang ist die Umrandung für einen Tisch? u Aufgabe 2: Landwirt Johannsen muss eine Weide neu einzäunen. Wie viele Meter Draht benötigt er, wenn die Weide 92 m lang und 84 m breit ist? Aufgabe 3: Übertrage die Tabelle in dein Heft und berechne die fehlenden Größen. Beachte dabei, dass du manchmal erst die Einheiten umwandeln musst. a) b) Länge 12 cm 30 cm Breite 8 cm Umfang c) 5 mm 8 dm Hinweis zu Aufgabe 3: Wenn der Umfang gegeben ist und eine Seite (Länge oder Breite) fehlt, dann berechnet man die fehlende Seite so: 40 mm d) e) 7 km 16 dm f) 4 9 10 g) 3 m 3, 5 km 24 mm 5 m 14 dm 10 cm Umfang =20 cm Länge = 4 cm Die Werte eintragen, die wir bereits kennen Lerntheke OER 5. 2

Station 16 u LÖSUNG Aufgabe 3: a) b) c) d) e) f) g) Länge 12 cm 30 cm 15 cm 7 km 16 dm = 1, 6 m 2, 6 cm 3 m Breite 8 cm 10 cm 5 mm 3, 5 km 0, 6 m 24 mm = 14 dm = 2, 4 cm 1, 4 m Umfang 40 cm 8 dm = 80 cm 40 mm 21 cm 5 m 10 cm 8, 8 m

Station 17 A FLÄCHENINHALT Aufgabe 1: Berechne den Flächeninhalt der folgenden Rechtecksflächen. Beispiel: Länge = 3 m, Breite = 2 m 9 Fläche = Länge · Breite A = a · b A = 3 m · 2 m A = 6 m² 11 Beim Ergebnis nicht die kleine 2 vergessen! a) b) c) Länge = 3 m Breite = 4 m Länge = 3 cm Breite = 1, 5 cm Länge = 8 mm Breite = 15 mm Aufgabe 2: Berechne den Flächeninhalt der folgenden Quadrate a) a = 5 cm b) a = 80 dm c) a = 9 m Aufgabe 3: Berechne den Flächeninhalt von folgendem Rechteck und Quadrat. Lerntheke OER 5. 2
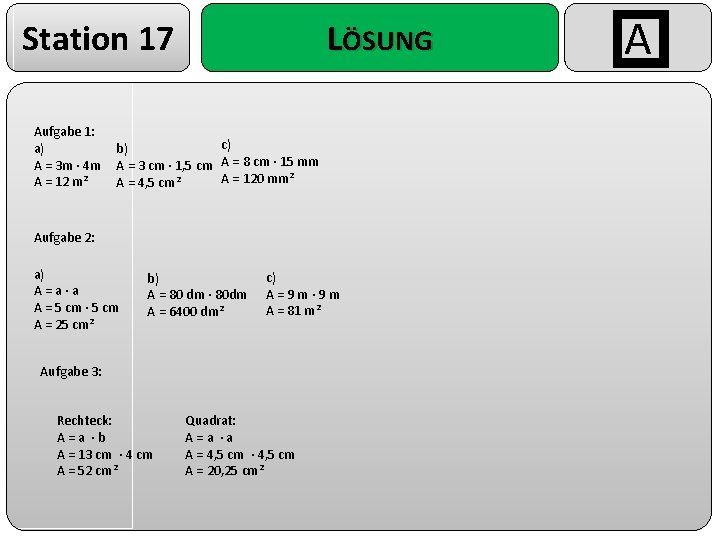
Station 17 Aufgabe 1: a) A = 3 m · 4 m A = 12 m² LÖSUNG c) b) A = 3 cm · 1, 5 cm A = 8 cm · 15 mm A = 120 mm² A = 4, 5 cm² Aufgabe 2: a) A = a · a A = 5 cm · 5 cm A = 25 cm² b) A = 80 dm · 80 dm A = 6400 dm² c) A = 9 m · 9 m A = 81 m² Aufgabe 3: Rechteck: A = a · b A = 13 cm · 4 cm A = 52 cm² Quadrat: A = a · a A = 4, 5 cm · 4, 5 cm A = 20, 25 cm² A
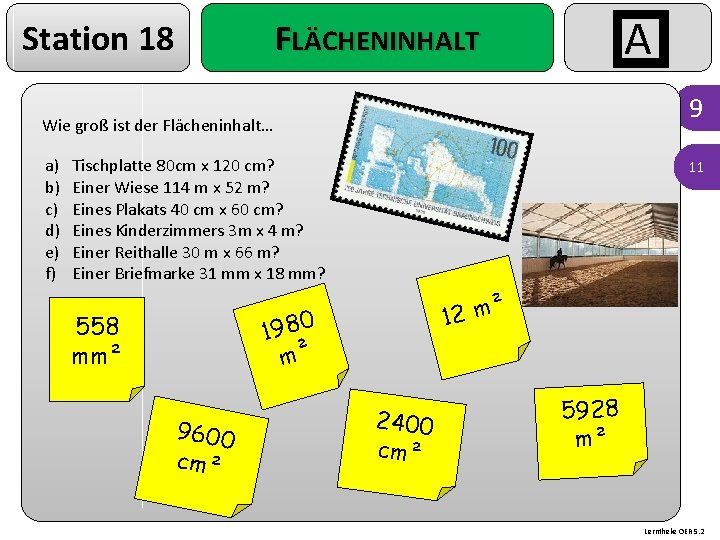
Station 18 A FLÄCHENINHALT 9 Wie groß ist der Flächeninhalt… a) b) c) d) e) f) Tischplatte 80 cm x 120 cm? Einer Wiese 114 m x 52 m? Eines Plakats 40 cm x 60 cm? Eines Kinderzimmers 3 m x 4 m? Einer Reithalle 30 m x 66 m? Einer Briefmarke 31 mm x 18 mm? 11 ² 12 m 1980 m² 558 mm² 9600 cm² 2400 cm² 5928 m² Lerntheke OER 5. 2

Station 18 LÖSUNG A a) Tischplatte 80 cm x 120 cm? A = 80 cm · 120 m A = 9600 cm² d) Eines Kinderzimmers 3 m x 4 m? A = 3 m · 4 m A = 12 m² b)Einer Wiese 114 m x 52 m? A = 114 m · 52 m A = 5928 m² e) Einer Reithalle 30 m x 66 m? A = 30 m · 66 m A = 1980 m² c) Eines Plakats 40 cm x 60 cm? A = 40 cm · 60 cm A = 2400 cm² f) Einer Briefmarke 31 mm x 18 mm? A = 31 mm · 18 mm A = 558 mm²

FLÄCHENINHALT RECHTECK & QUADRAT Station 19 Aufgabe 1: Der Fußboden einer Küche, die 2 m 8 dm Länge und 2 m 1 dm Breite hat, soll mit Fliesen ausgelegt werden. Für wie viele Quadratmeter müssen Fliesen gekauft werden? Aufgabe 2: Berechne den Flächeninhalt der nebenstehenden Fläche. A 11 Aufgabe 3: Zeichne folgende Rechtecke und berechne ihre Flächeninhalte. Länge Breite 2 cm 3 cm 2, 5 cm 2 cm 1, 5 cm 3, 5 cm 1, 5 cm 4 cm Fläche Lerntheke OER 5. 2
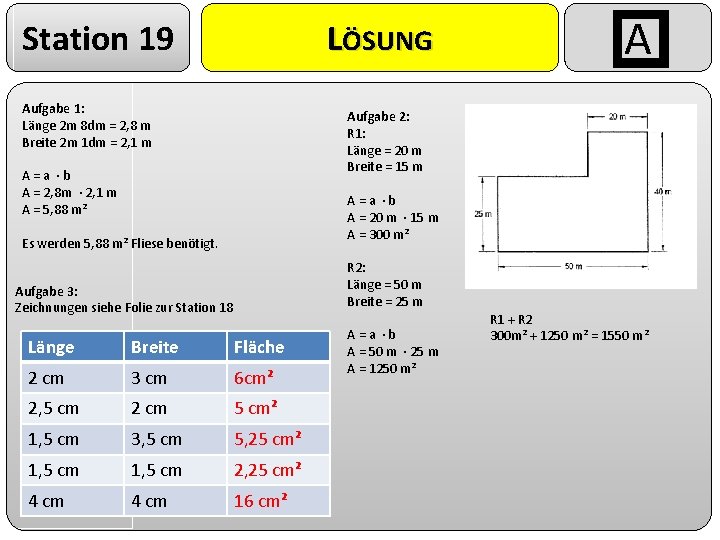
Station 19 LÖSUNG Aufgabe 1: Länge 2 m 8 dm = 2, 8 m Breite 2 m 1 dm = 2, 1 m A Aufgabe 2: R 1: Länge = 20 m Breite = 15 m A = a · b A = 2, 8 m · 2, 1 m A = 5, 88 m² A = a · b A = 20 m · 15 m A = 300 m² Es werden 5, 88 m² Fliese benötigt. R 2: Länge = 50 m Breite = 25 m Aufgabe 3: Zeichnungen siehe Folie zur Station 18 Länge Breite Fläche 2 cm 3 cm 6 cm² 2, 5 cm 2 cm 5 cm² 1, 5 cm 3, 5 cm 5, 25 cm² 1, 5 cm 2, 25 cm² 4 cm 16 cm² A = a · b A = 50 m · 25 m A = 1250 m² R 1 + R 2 300 m² + 1250 m² = 1550 m²

Station 20 RECHNEN MIT GELD 1 1) Bernd will Süßigkeiten kaufen. Ein Schokoriegel kostet 45 Cent. Ein Dreier-Pack kostet 1, 26€. a) Wie teuer ist ein Schokoriegel im Dreier-Pack? 2 b) Bernd hat 5 Euro und 44 Cent dabei. Wie viele Schokoriegel könnte er kaufen? Tipp: Er kauft natürlich die für ihn günstigeren Riegel! 6 a) Bernd hat es sich nun doch anders überlegt. Er kauft mit seinem Geld lieber eine Zahnbürste für 1, 74€ und Zahnpasta für 94 Cent. Wie viele Schokoriegel kann er von dem Rest kaufen? 7 Lerntheke OER 5. 1

Station 20 LÖSUNG 1. 1, 26 € = 126 ct Antwort: Ein Schokoriegel im Dreierpack kostet 0, 42 € 1 2 6 : 3 = 42 0 4 2 Er kauft natürlich 3´er Packen, da in diesen der Riegel nur 42 ct kostest. 1 2 1 2 4 8 4 4 0 Antwort: Er kauft vier Dreierpackungen, also 12 Riegel. Restgeld: 40 ct 0 6 6 0 3. 5 4 4 : 42 = 12 R 40 ct 2. 5, 44 € = 544 ct 5, 44 € 1, 74 € + 0, 94 € 1 2, 68 € - 2, 68 € 1 1 2, 76 € = 276 ct 2 7 6 : 42 = 6 R 24 ct 2 5 2 2 4 Antwort: Er kann noch zwei Dreierpackungen, also 6 Riegel kaufen. Restgeld 24 ct
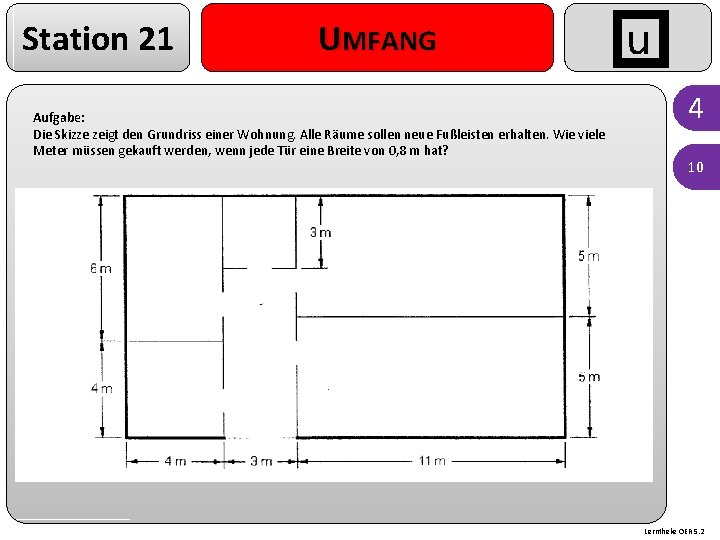
Station 21 UMFANG Aufgabe: Die Skizze zeigt den Grundriss einer Wohnung. Alle Räume sollen neue Fußleisten erhalten. Wie viele Meter müssen gekauft werden, wenn jede Tür eine Breite von 0, 8 m hat? u 4 10 Lerntheke OER 5. 2
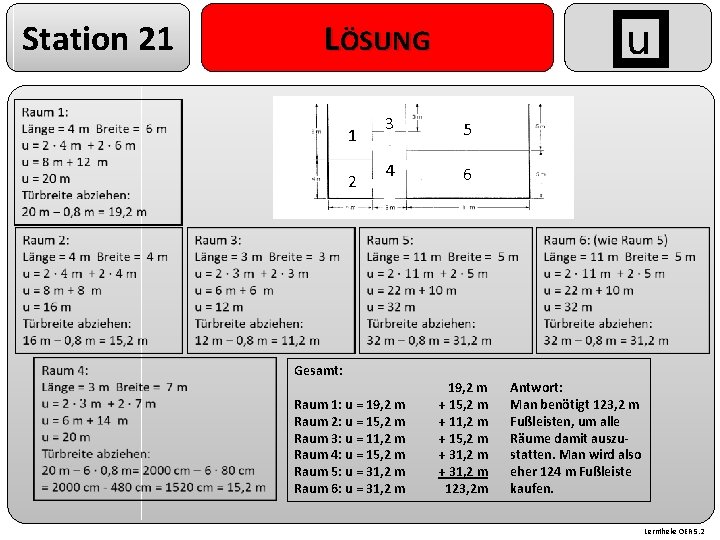
Station 21 1 2 u LÖSUNG 3 5 4 6 Gesamt: Raum 1: u = 19, 2 m Raum 2: u = 15, 2 m Raum 3: u = 11, 2 m Raum 4: u = 15, 2 m Raum 5: u = 31, 2 m Raum 6: u = 31, 2 m 19, 2 m + 15, 2 m + 11, 2 m + 15, 2 m + 31, 2 m 123, 2 m Antwort: Man benötigt 123, 2 m Fußleisten, um alle Räume damit auszustatten. Man wird also eher 124 m Fußleiste kaufen. Lerntheke OER 5. 2

Station 22 Aufgabe: Berechne den Flächeninhalt! FLÄCHENINHALT A 11 Lerntheke OER 5. 2

Station 22 LÖSUNG Aufgabe: Berechne den Flächeninhalt! A 1 = 7 m · 1 m A 1 = 7 m² A 2 = 0, 5 m · 6 m A 2 = 3 m² A A=A 1 + A 2 + A 3 + A 4 A= 7 m² + 3 m² + 2 m² + 1 m² A = 13 m² A 3 = 0, 5 m · 4 m A 3 = 2 m² A 4 =0, 5 m · 2 m A 4 = 1 m² A 1 = 1, 5 m · 2, 5 m A 1= 3, 75 m² A 1 · 3 = 3, 75 m² · 3 = 11, 25 m² A 1 + A 2 = 11, 25 m² + 3 m³ = 14, 25 m² A 2= 1 m · 1, 5 m A 2= 1, 5 m² A 1 · 1 =1, 5 m² · 2 = 3 m² Lerntheke OER 5. 2
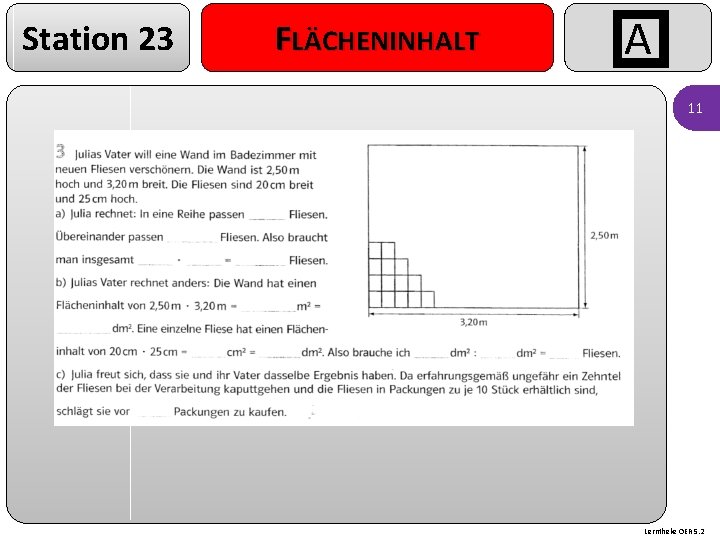
Station 23 FLÄCHENINHALT A 11 Lerntheke OER 5. 2
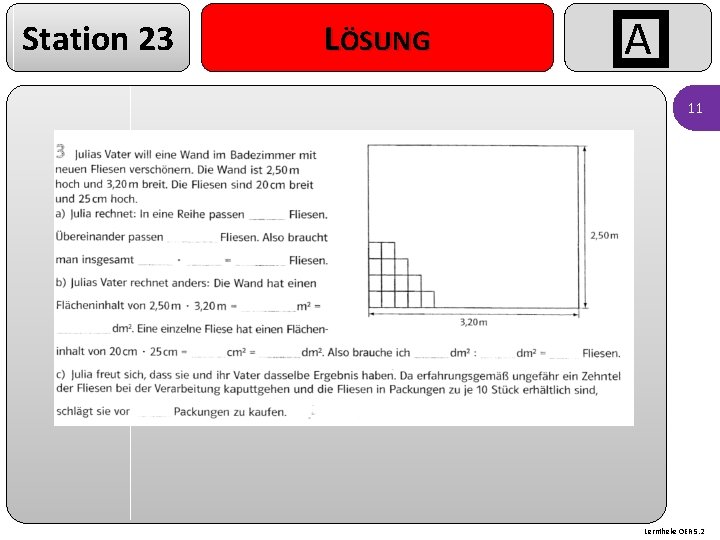
Station 23 LÖSUNG A 11 Lerntheke OER 5. 2
- Slides: 65