HighOrder Spatial and Temporal Methods for Simulation and

High-Order Spatial and Temporal Methods for Simulation and Sensitivity Analysis of High-Speed Flows PI Dimitri J. Mavriplis University of Wyoming Co-PI Luigi Martinelli Princeton University

Project Scope and Relevance • Develop novel approaches for improving simulation capabilities for high-speed flows – Emerging consensus about higher-order methods • May be only way to get desired accuracy – Asymptotic arguments • Superior scalability – Sensitivity analysis and adjoint methods • Now seen as indispensible component of new emerging class of simulation tools • Automated (adaptive) solution process with certifiable accuracy – Other novel approaches: BGK methods

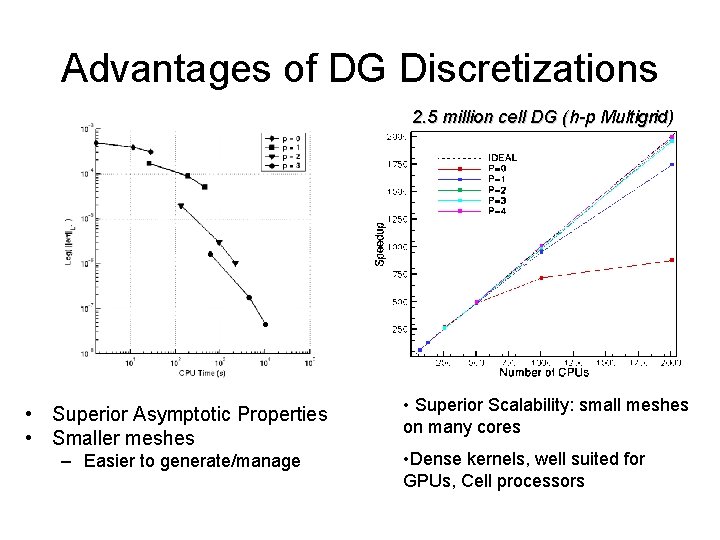
Advantages of DG Discretizations 2. 5 million cell DG (h-p Multigrid) • Superior Asymptotic Properties • Smaller meshes – Easier to generate/manage • Superior Scalability: small meshes on many cores • Dense kernels, well suited for GPUs, Cell processors

Disadvantages of DG Discretizations • High-Risk, Revolutionary – Still no production level DG code for subsonics • Relies on smooth solution behavior to achieve favorable asymptotic accuracy – Difficulties for strong shocks – Robustness issues

Overview of Current Work 1. 2. 3. 4. Viscous discretizations and solvers for DG ALE Formulation for moving meshes BGK Flux flunction implementation/results Shock capturing - Artificial dissipation - High-order filtering/limiting 5. Adjoint-based h-p refinement - Shocks captured with no limiting/added dissipation 6. Conclusions

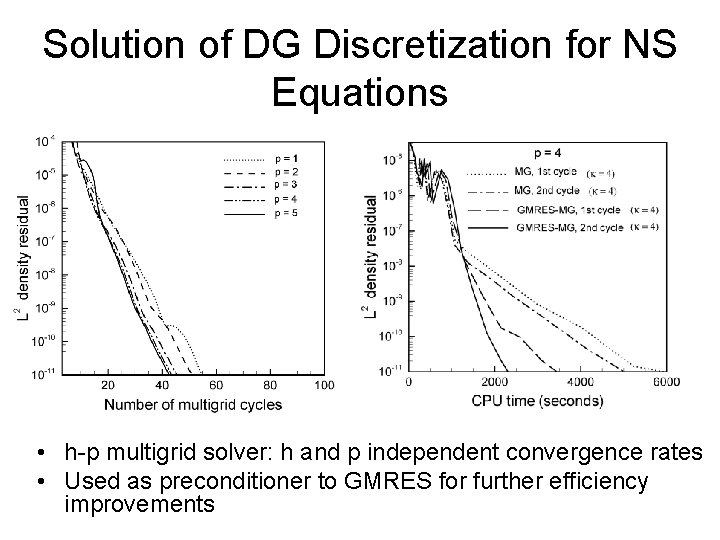
Extension to Viscous Flows • DG methods developed initially for hyperbolic problems – Diffusion terms for DG non-trivial • Interior Penalty (IP) method – Simplest approach, compact stencil – Explicit expression for penalty parameter derived (JCP) • IP method derived and implemented for compressible Navier-Stokes formulation up to p=5 – Studied symmetric and non-symmetric forms for IP – h and p independent convergence observed for Poisson and Navier. Stokes problems

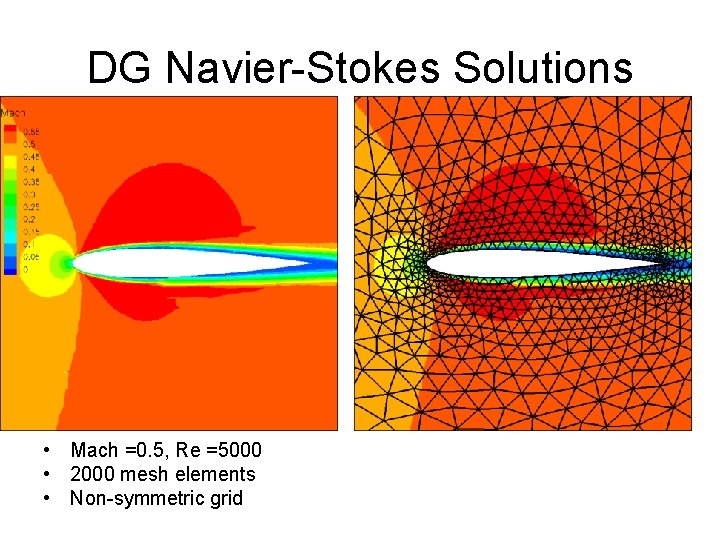
DG Navier-Stokes Solutions • Mach =0. 5, Re =5000 • 2000 mesh elements • Non-symmetric grid

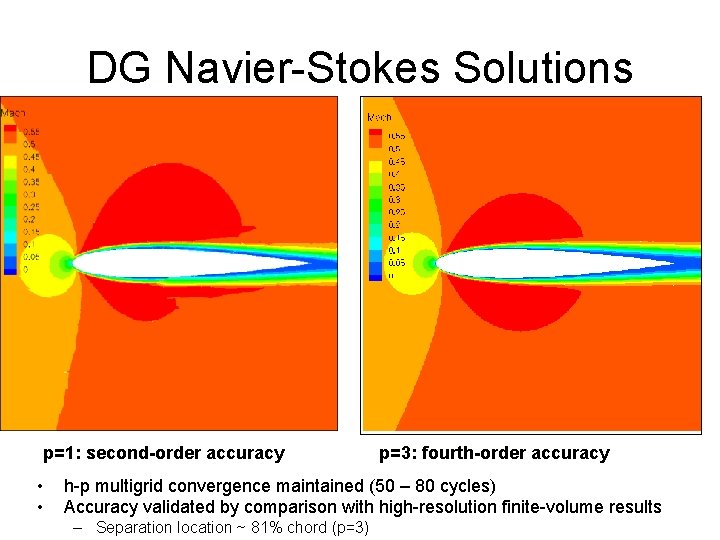
DG Navier-Stokes Solutions p=1: second-order accuracy • • p=3: fourth-order accuracy h-p multigrid convergence maintained (50 – 80 cycles) Accuracy validated by comparison with high-resolution finite-volume results – Separation location ~ 81% chord (p=3)

Solution of DG Discretization for NS Equations • h-p multigrid solver: h and p independent convergence rates • Used as preconditioner to GMRES for further efficiency improvements

Kinetic Based Flux Formulations (BGK) L. Martinelli Princeton University • Alternative for extension to Navier-Stokes: – It is not necessary to compute the rate of strain tensor in order to calculate viscous fluxes • Automatic upwinding via the kinetic model. • Satisfy Entropy Condition (H-Theorem) at the discrete level. • Implemented in 2 D Unstructured Finite-Volume code by Martinelli • Extension to 2 D DG code under development

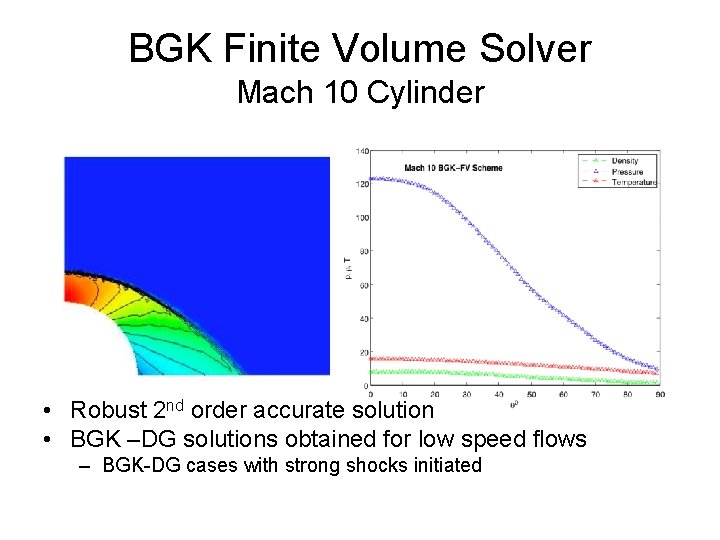
BGK Finite Volume Solver Mach 10 Cylinder • Robust 2 nd order accurate solution • BGK –DG solutions obtained for low speed flows – BGK-DG cases with strong shocks initiated

Treatment of Shock Waves • High-order (DG) methods based on smooth solution behavior • 3 approaches investigated for high-order shock wave simulation – Smoothing out shock: Artificial viscosity • Use IP method discussed previously • Sub-cell shock resolution possible – Limiting or Filtering High Order Solution • Remove spurious oscillations • Sub-cell shock resolution possible – h-p adaption • • Start with p=0 (1 st order) solution Raise p (order) only were solution is smooth Refine mesh (h) where solution is non-smooth (shock) No limiting required!

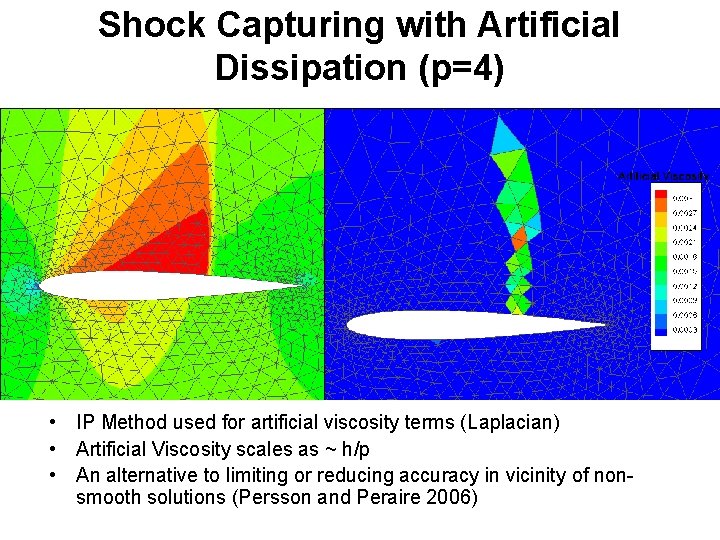
Shock Capturing with Artificial Dissipation (p=4) • IP Method used for artificial viscosity terms (Laplacian) • Artificial Viscosity scales as ~ h/p • An alternative to limiting or reducing accuracy in vicinity of nonsmooth solutions (Persson and Peraire 2006)

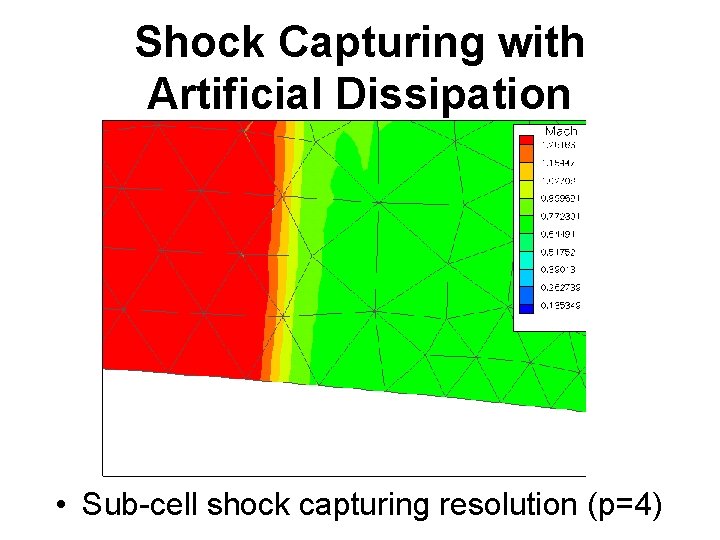
Shock Capturing with Artificial Dissipation • Sub-cell shock capturing resolution (p=4)

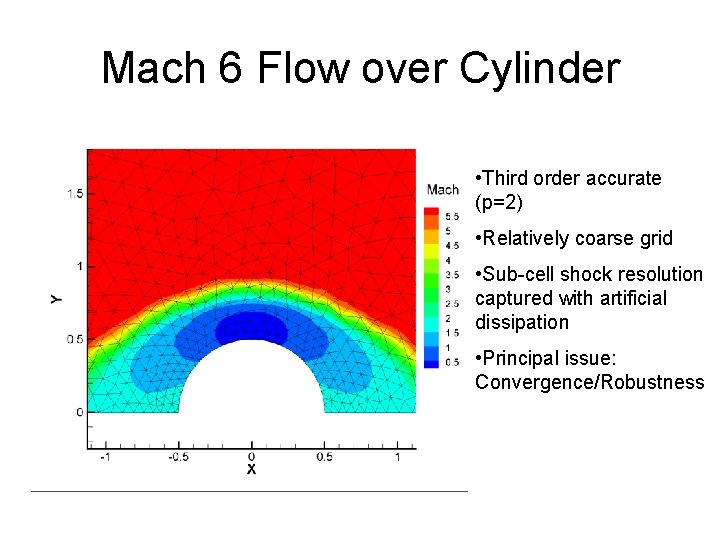
Mach 6 Flow over Cylinder • Third order accurate (p=2) • Relatively coarse grid • Sub-cell shock resolution captured with artificial dissipation • Principal issue: Convergence/Robustness

Total Variation based nonlinear Filtering l Formulation Ø Minimization where, Ø Euler-Lagrange equation (1 st variation) Nonlinear partial differential equations (PDE) based Ø Pseudo-time stepping (Rudin, Osher and Fatemi 1992) Ø Solved locally in each element

Total Variation based nonlinear Filtering l Formulation Ø Controls amount of filtering Minimization where, Ø Euler-Lagrange equation (1 st variation) Nonlinear partial differential equations (PDE) based Ø Pseudo-time stepping (Rudin, Osher and Fatemi 1992) Ø Solved locally in each element

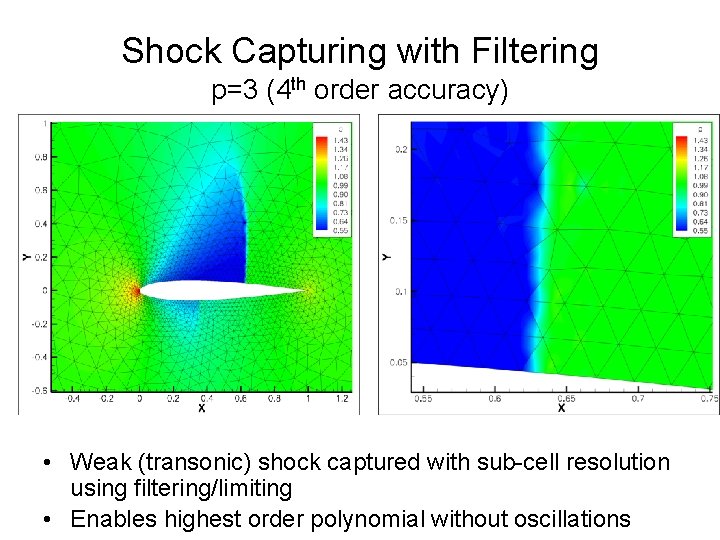
Shock Capturing with Filtering p=3 (4 th order accuracy) • Weak (transonic) shock captured with sub-cell resolution using filtering/limiting • Enables highest order polynomial without oscillations

DG Filtering for High Speed Flows • Mach 6 flow over cylinder at p=2 (3 rd order) – Lax Friedrichs flux Relatively robust Shock spread over more than one element

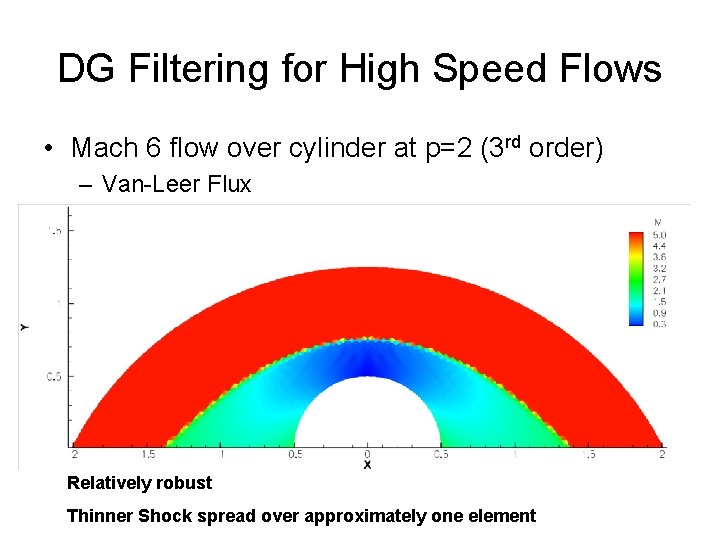
DG Filtering for High Speed Flows • Mach 6 flow over cylinder at p=2 (3 rd order) – Van-Leer Flux Relatively robust Thinner Shock spread over approximately one element

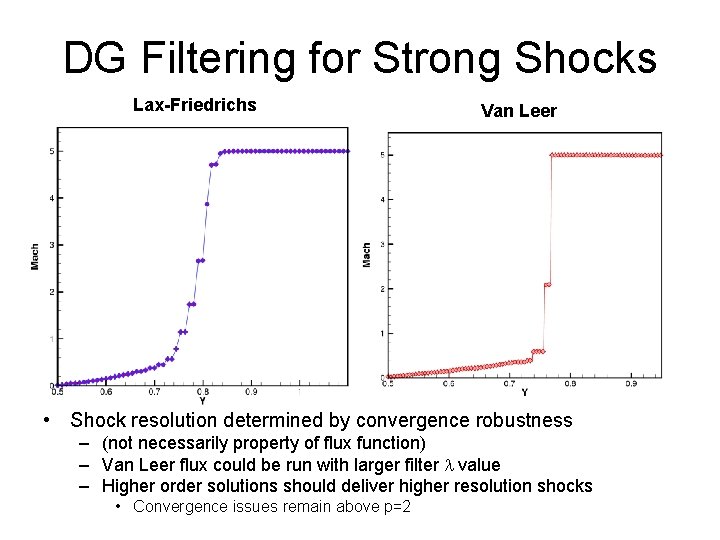
DG Filtering for Strong Shocks Lax-Friedrichs Van Leer • Shock resolution determined by convergence robustness – (not necessarily property of flux function) – Van Leer flux could be run with larger filter l value – Higher order solutions should deliver higher resolution shocks • Convergence issues remain above p=2

ADJOINT-BASED ERROR ESTIMATION • Formulation – Key objective functionals with engineering applications • Surface integrals of the flow-field variables • Lift, drag, integrated temperature, surface heat flux • A single objective, expressed as – Current mesh (coarse mesh, H) • Coarse flow solution, • Objective on the coarse mesh, – Globally refined mesh (fine mesh, h) • Fine flow solution, • Objective on the fine mesh, • Goal : find an approximate for NOT DESIRED! without solving on the fine mesh 22

ADJOINT-BASED ERROR ESTIMATION • Formulation – Coarse grid solution projected onto fine grid gives non-zero residual – Change in objective calculated on fine grid: = inner product of residual with adjoint • Procedure – Compute coarse grid solution and adjoint – Project solution and adjoint to fine grid – Form inner product of residual and adjoint on fine grid • Global Error estimate of objective • Local error estimate (in each cell) – Use to drive adaptive refinement – Smoothness indicator used to choose between h and p refinement – Naturally maintains p=0 in shock region 23

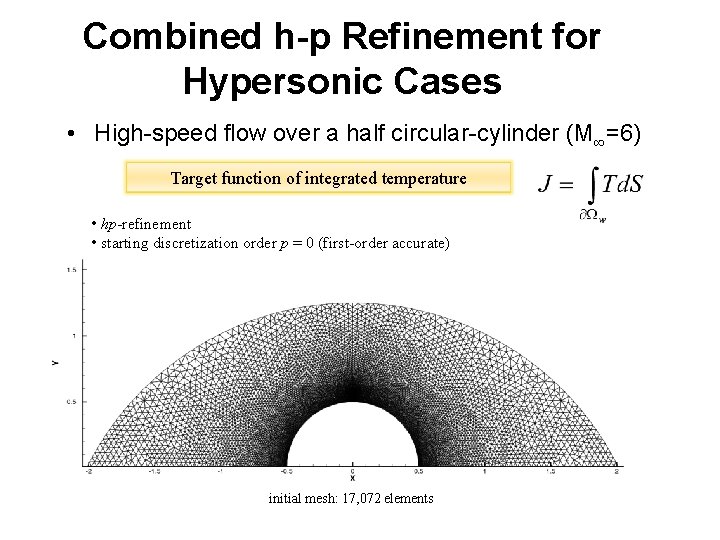
Combined h-p Refinement for Hypersonic Cases • High-speed flow over a half circular-cylinder (M∞=6) Target function of integrated temperature • hp-refinement • starting discretization order p = 0 (first-order accurate) initial mesh: 17, 072 elements 24

h-p Refinement for High-Speed Flows • High-speed flow over a half circular-cylinder (M∞=6) No shock refinement in regions not affecting surface temperature adapted mesh: 42, 234 elements, discretization orders p=0~3 25

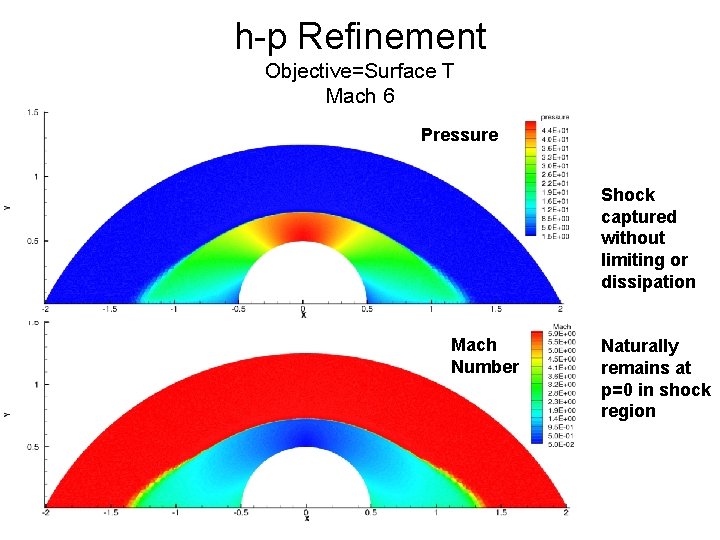
h-p Refinement Objective=Surface T Mach 6 Pressure Shock captured without limiting or dissipation Mach Number Naturally remains at p=0 in shock region 26

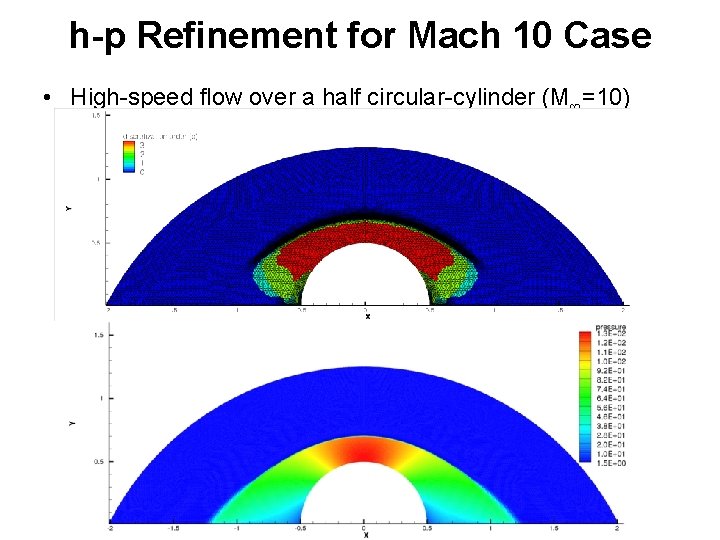
h-p Refinement for Mach 10 Case • High-speed flow over a half circular-cylinder (M∞=10) Target function of drag 27

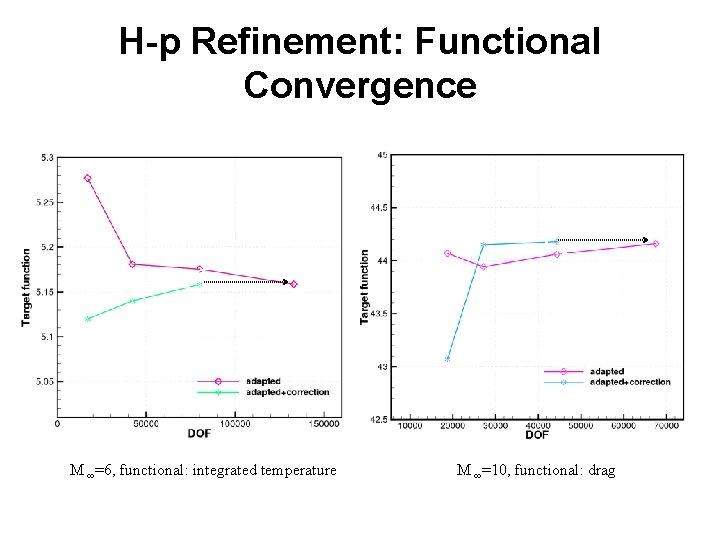
H-p Refinement: Functional Convergence M ∞=6, functional: integrated temperature M ∞=10, functional: drag 28

Conclusions and Future Work • DG methods hold promise for advancing state-ofthe-art for difficult problems such as Hypersonics • Recent advances in: – – – Viscous discretizations Flux functions (BGK) ALE formulations Solver technology (h-p multigrid) Shock capturing • Extend into 3 D DG parallel code – Diffusion terms – Shock capturing – h-p adaptivity (adjoint based) • Real gas effects – 5 species, 2 temperature model for DG code

Remaining Difficulties • DG Methods need to be robust – Often requires accuracy reduction (limiting) • Shock capturing with artificial viscosity becomes very nonlinear/difficult to converge for high p and high Mach • Limiting is very robust initially, but convergence to machine zero stalls – Other limiter formulations are possible • Adjoint h-p refinement is promising but will likely require use with limiter for necessary robustness – Linearization of limiter/filter