HighOrder Explicit RungeKutta Methods Using mSymmetry T Feagin





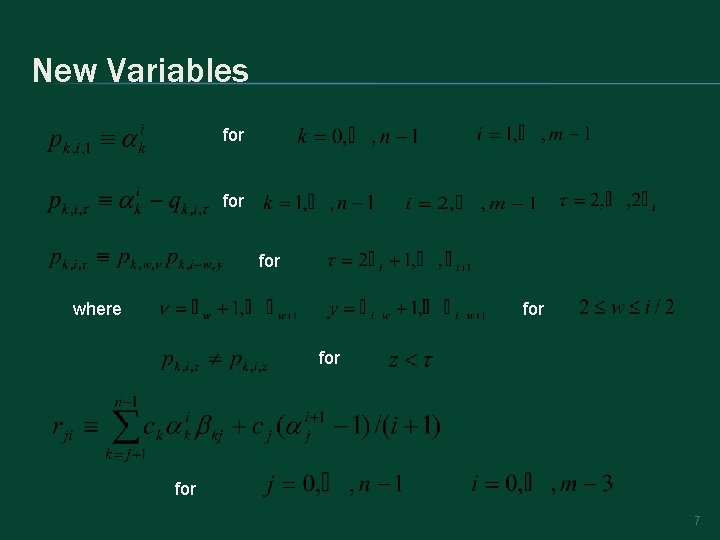











- Slides: 28

High-Order Explicit Runge-Kutta Methods Using m-Symmetry T. Feagin University of Houston – Clear Lake Houston, Texas, USA June 24, 2009 1

Overview • • Background and introduction The Runge-Kutta equations of condition New variables Reformulated equations m-symmetry Finding an m-symmetric method Numerical experiments 2

The Initial Value Problem 3

Explicit Runge-Kutta Methods t 0 + h h - the stepsize where 4

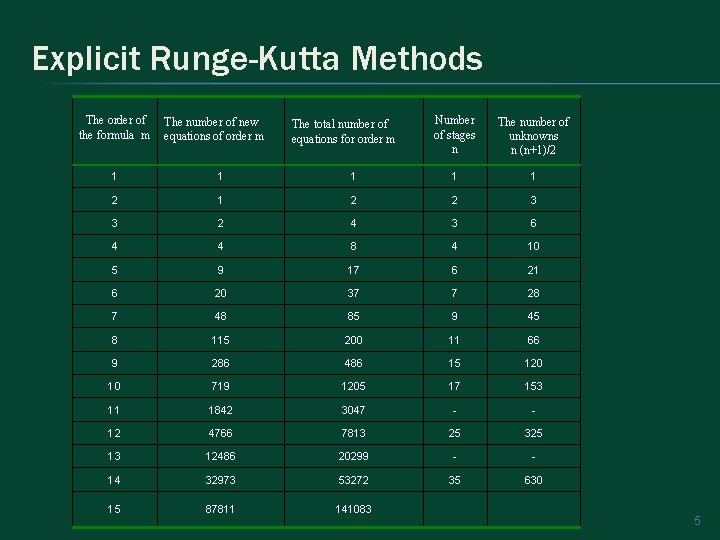
Explicit Runge-Kutta Methods The order of the formula m The number of new equations of order m The total number of equations for order m Number of stages n The number of unknowns n (n+1)/2 1 1 1 2 2 3 3 2 4 3 6 4 4 8 4 10 5 9 17 6 21 6 20 37 7 28 7 48 85 9 45 8 115 200 11 66 9 286 486 15 120 10 719 1205 17 153 11 1842 3047 - - 12 4766 7813 25 325 13 12486 20299 - - 14 32973 53272 35 630 15 87811 141083 5

Equations of Condition for 6
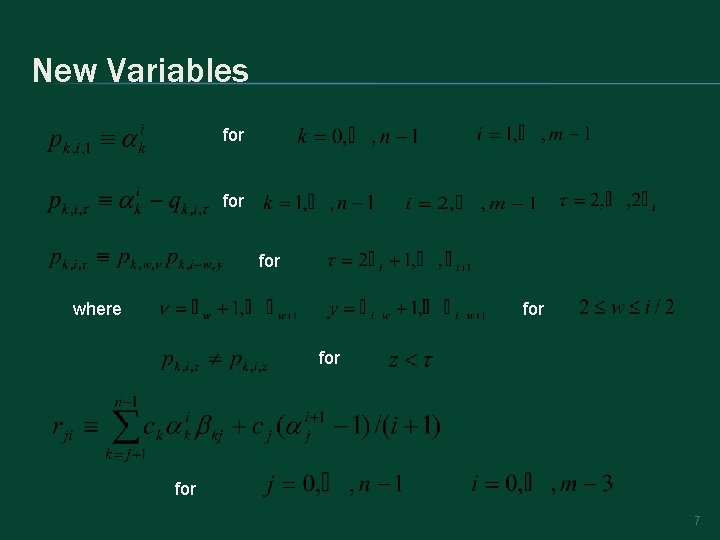
New Variables for for where for for 7

New Variables for one of the row simplifying assumptions when zero for where for one of the column simplifying assumptions when zero for 8

Reformulated Equations of Condition for all other values of in the range 9

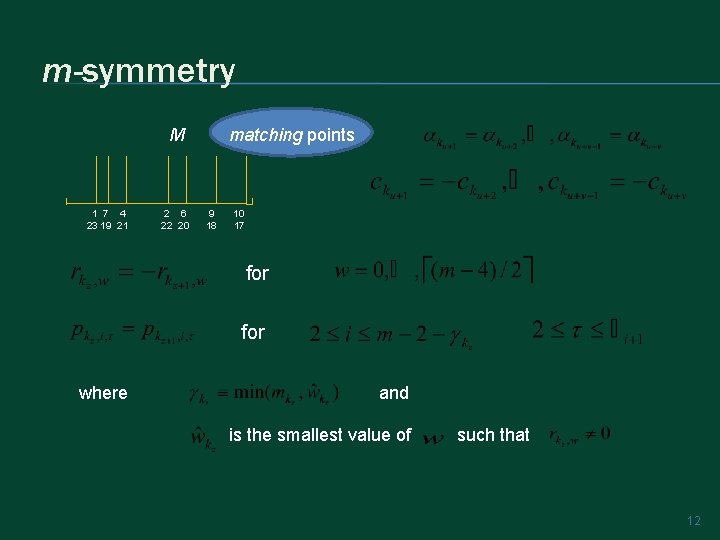
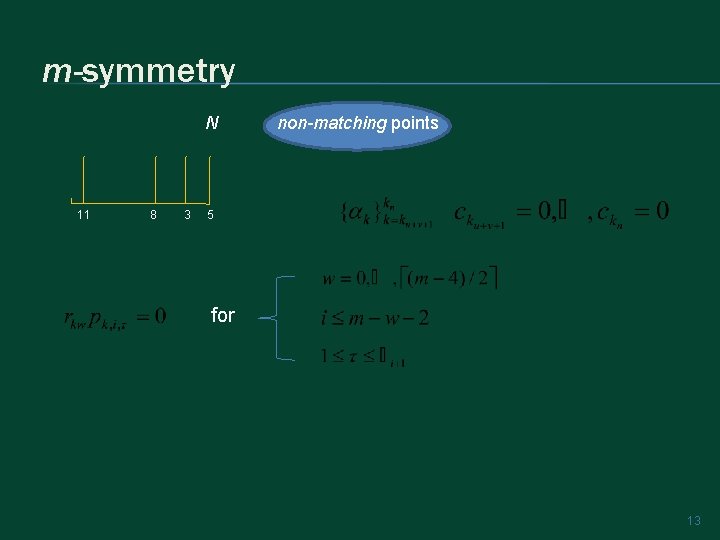
Theorem: Any m-symmetric Runge-Kutta method is of order m. m-symmetry The set of integer subscripts Q quadrature points can be partitioned into three subsets M matching points N non-matching points 10

m-symmetry Q 0 12 13 14 quadrature points 15 16 24 for 11

m-symmetry M 1 7 4 23 19 21 2 6 22 20 matching points 9 18 10 17 for where and is the smallest value of such that 12

m-symmetry N 11 8 3 non-matching points 5 for 13

New Equations for a 6 th Order Method 14

Finding an m-symmetric Method • • • Determine a quadrature formula of order m or higher with u weights and u nodes Gauss-Lobatto formulae are a possible and usually convenient choice Determine (or establish equations governing the values of) the points leading up to αk 2 (the first internal quadrature point) such that the order at the quadrature points is m/2 15

Finding an m-symmetric Method (cont’d) • • Identify the matching and non-matching points Obtain values for any of the αk‘s yet to be determined (i. e. , solve nonlinear equations) Select non-zero values for the free parameters (c k‘s at the matching points) such that , … Solve the remaining equations from the definition to make the method m- 16

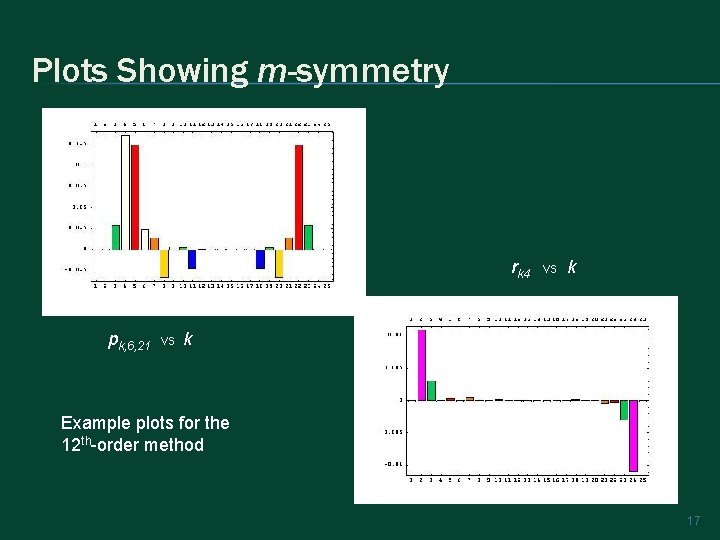
Plots Showing m-symmetry rk 4 pk, 6, 21 vs vs k k Example plots for the 12 th-order method 17

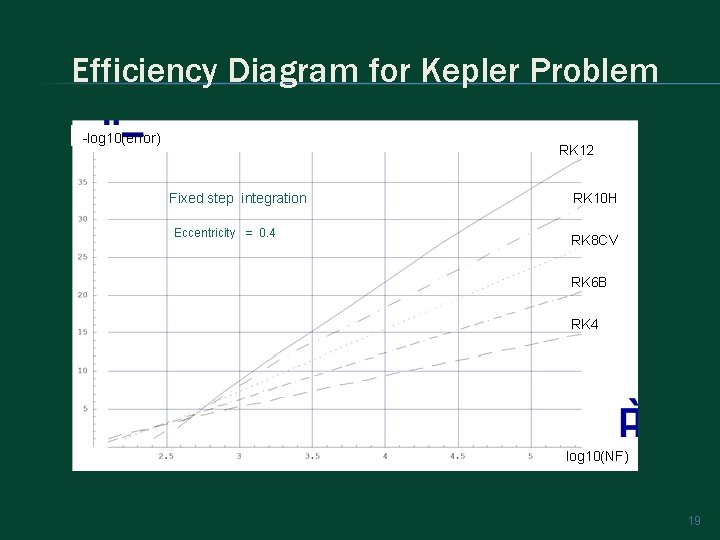
RK 12(10) - Optimizing the Method • Seeking to reduce the local truncation errors by minimizing size and number of the unsatisfied 13 th-order terms (more than 92% are satisfied) • Trying to keep the largest coefficient (in absolute value) to a reasonable level (~12) Trying to maintain a reasonably large absolute stability region Im(hλ) • Re(hλ) 18

Efficiency Diagram for Kepler Problem -log 10(error) RK 12 Fixed step integration Eccentricity = 0. 4 RK 10 H RK 8 CV RK 6 B RK 4 log 10(NF) 19

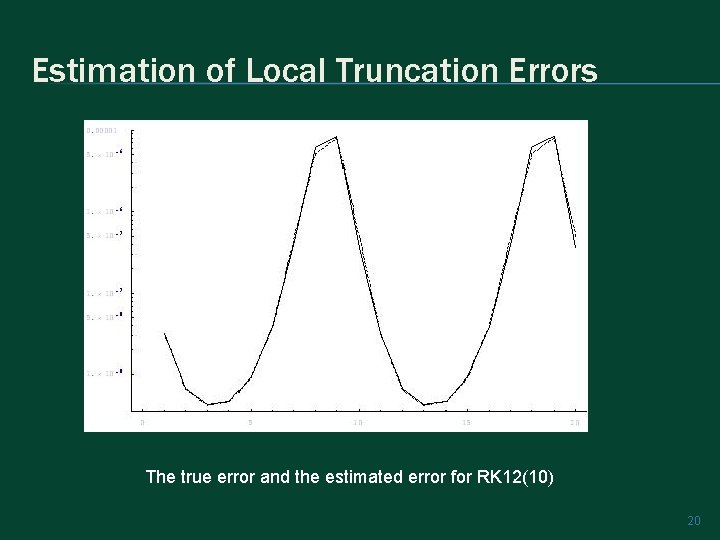
Estimation of Local Truncation Errors The true error and the estimated error for RK 12(10) 20

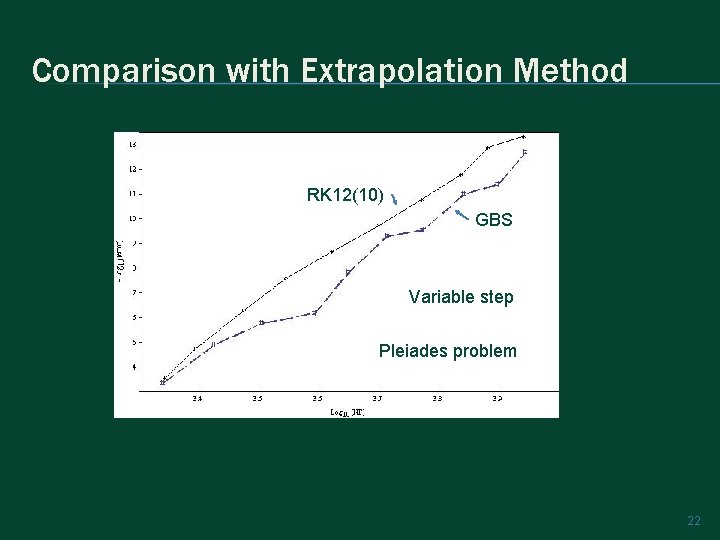
The Pleiades Problem 21

Comparison with Extrapolation Method RK 12(10) GBS Variable step Pleiades problem 22

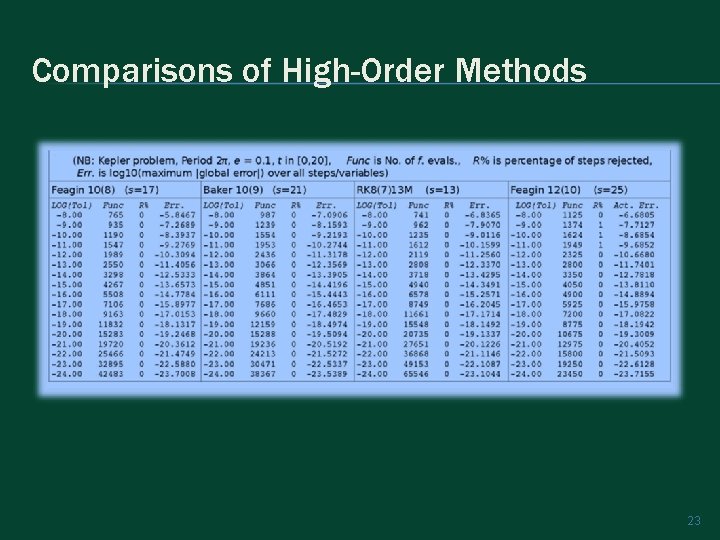
Comparisons of High-Order Methods 23

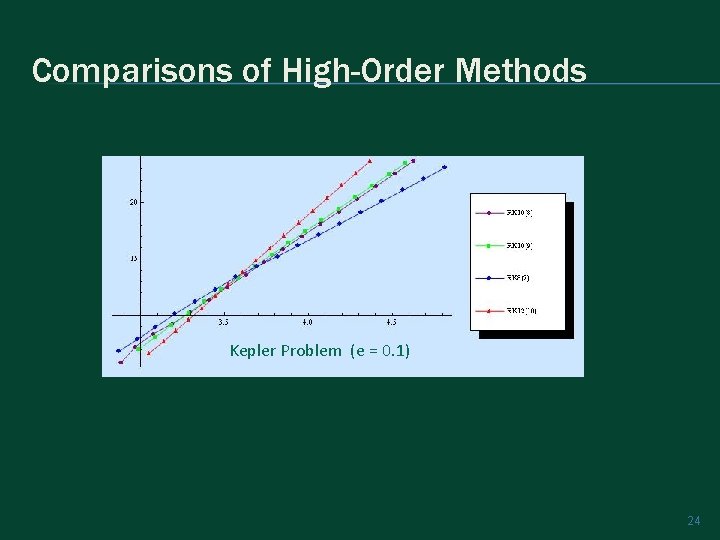
Comparisons of High-Order Methods Kepler Problem (e = 0. 1) 24

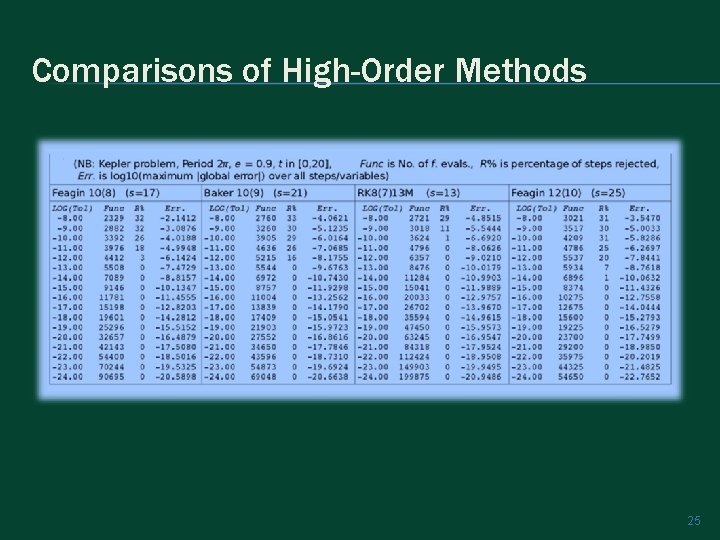
Comparisons of High-Order Methods 25

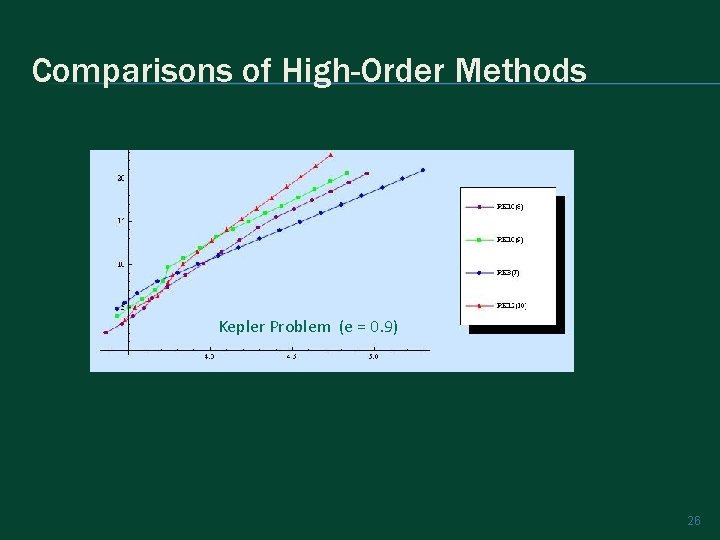
Comparisons of High-Order Methods Kepler Problem (e = 0. 9) 26

References W. B. Gragg, On extrapolation algorithms for ordinary initial value problems. SIAM J. Num. Anal. , 2 (1965) pp. 384 -403 E. Baylis Shanks, Solutions of Differential Equations by Evaluations of Functions, Math. Comp. 20, No. 93 (1966), pp. 21 -38 E. Fehlberg, Classical Fifth-, Sixth-, Seventh- , and Eighth-Order Runge-Kutta Formulas with Stepsize Control, NASA TR R-287, (1968) E. Hairer, A Runge-Kutta method of order 10, J. Inst. Math. Applics. 21 (1978) pp. 47 -59 Hiroshi Ono, On the 25 stage 12 th order explicit Runge--Kutta method, JSIAM Journal, Vol. 16, No. 3, 2006, p. 177 -186 J. H. Verner, The derivation of high order Runge Kutta methods, Univ. of Auckland, New Zealand, Report No. 93, (1976) P. J. Prince and J. R. Dormand, High-order embedded Runge-Kutta formulae, J Comput. Appl. Math. , 7 (1981), pp. 67 -76 T. Feagin, , A Tenth-Order Runge-Kutta Method with Error Estimate, Proceedings (Edited Version) of the International Multi. Conference of Engineers and Computer Scientists 2007, Hong Kong 27

Where to Obtain Coefficients, etc. http: //sce. uhcl. edu/rungekutta feagin@uhcl. edu Im(hλ) Re(hλ) 28