HIGHER The Straight Line Functions and Graphs Composite

HIGHER The Straight Line Functions and Graphs Composite Functions Trigonometry Recurrence Relations Basics before Differentiation 1 Polynomials and Quadratic Theory Basics before Integration 1 Trig Equations & Equations The Circle Vectors 1 Vectors 2 Further Differentiation Logs & Exponentials Wave Functions

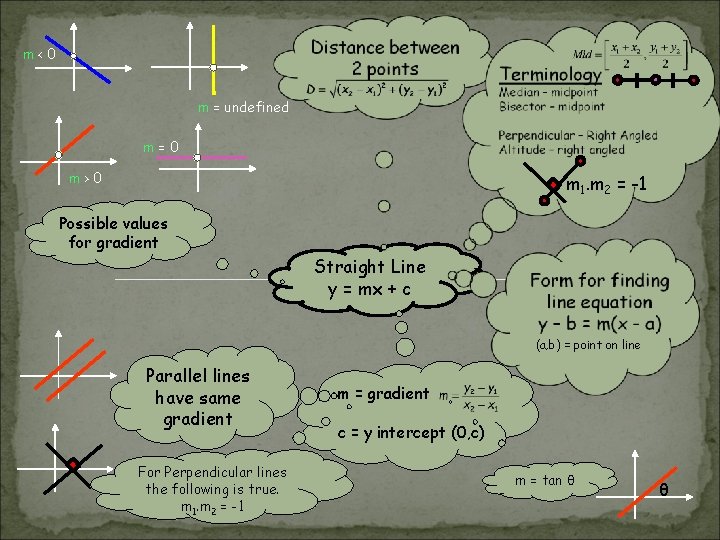
m<0 m = undefined m=0 m>0 m 1. m 2 = -1 Possible values for gradient Straight Line y = mx + c (a, b) = point on line Parallel lines have same gradient For Perpendicular lines the following is true. m 1. m 2 = -1 m = gradient c = y intercept (0, c) m = tan θ θ

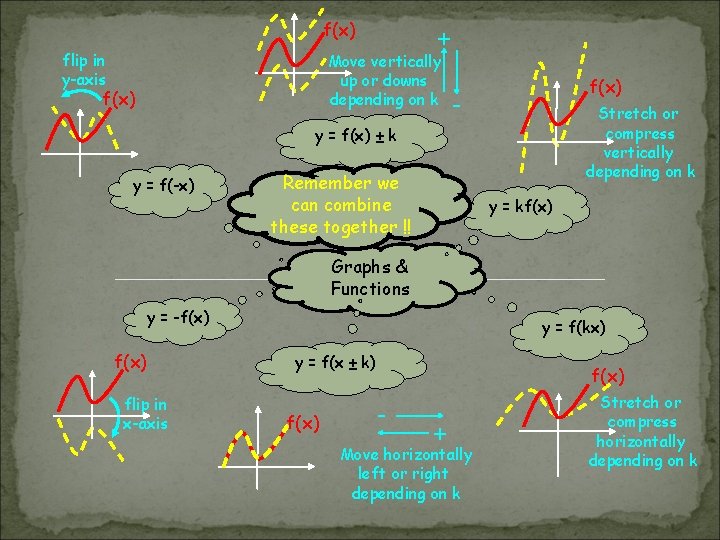
f(x) flip in y-axis + Move vertically up or downs depending on k f(x) - Stretch or compress vertically depending on k y = f(x) ± k y = f(-x) Remember we can combine these together !! y = kf(x) Graphs & Functions y = -f(x) flip in x-axis y = f(kx) y = f(x ± k) f(x) - + Move horizontally left or right depending on k Stretch or compress horizontally depending on k

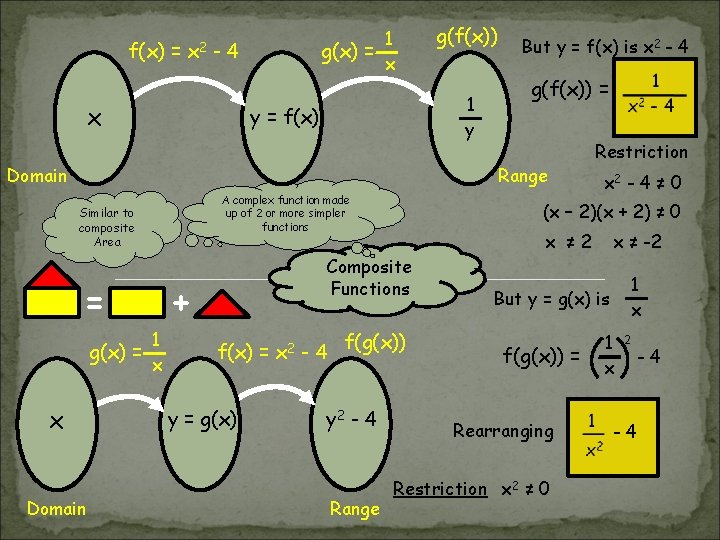
f(x) = x 2 1 g(x) = x -4 x g(f(x)) 1 y y = f(x) Domain But y = f(x) is x 2 - 4 g(f(x)) = Range A complex function made up of 2 or more simpler functions Similar to composite Area = 1 g(x) = x x Domain f(x) = y = g(x) x 2 x ≠ 2 - 4 f(g(x)) y 2 - 4 Range x 2 - 4 ≠ 0 (x – 2)(x + 2) ≠ 0 Composite Functions + Restriction x ≠ -2 1 x But y = g(x) is f(g(x)) = Rearranging Restriction x 2 ≠ 0 1 x 2 -4 -4

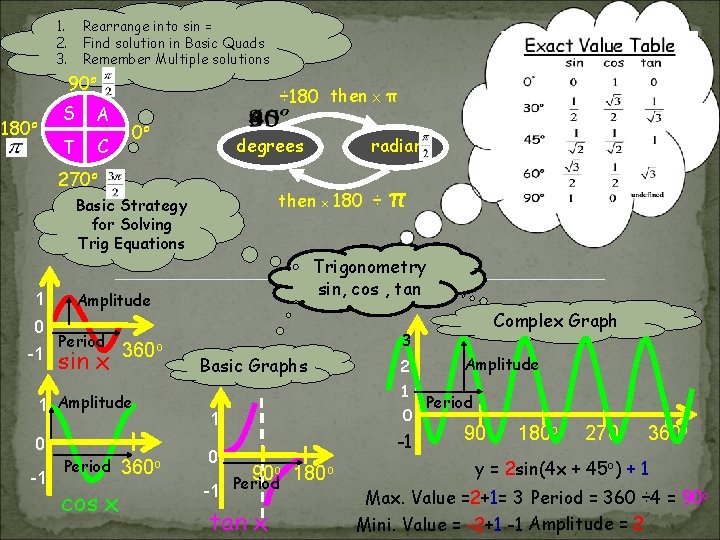
1. 2. 3. Rearrange into sin = Find solution in Basic Quads Remember Multiple solutions 90 o 180 o S A T C ÷ 180 then 0 o then x 180 ÷ π Basic Strategy for Solving Trig Equations 1 1 Amplitude 0 -1 Trigonometry sin, cos , tan Amplitude 0 Period o -1 sin x 360 Period cos x 360 o π radians degrees 270 o X Complex Graph 3 Basic Graphs -1 Amplitude 1 Period 0 1 0 2 -1 o 180 o 90 Period tan x 90 o 180 o 270 o 360 o y = 2 sin(4 x + 45 o) + 1 Max. Value =2+1= 3 Period = 360 ÷ 4 = 90 o Mini. Value = -2+1 -1 Amplitude = 2

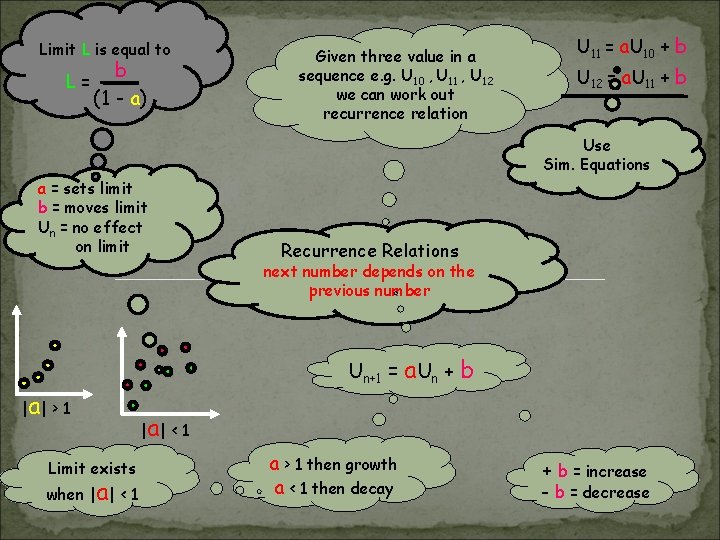
Limit L is equal to L= b (1 - a) Given three value in a sequence e. g. U 10 , U 11 , U 12 we can work out recurrence relation U 11 = a. U 10 + b U 12 = a. U 11 + b Use Sim. Equations a = sets limit b = moves limit Un = no effect on limit Recurrence Relations next number depends on the previous number Un+1 = a. Un + |a | > 1 Limit exists when |a| < 1 b |a | < 1 a > 1 then growth a < 1 then decay + b = increase - b = decrease

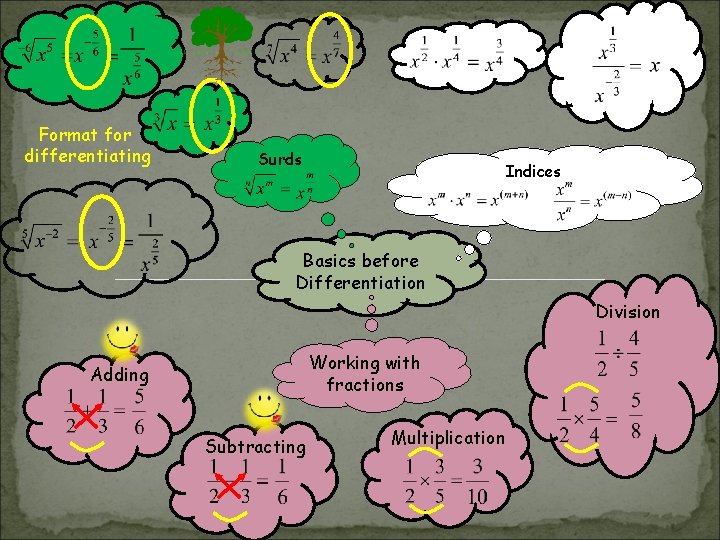
Format for differentiating Surds Indices Basics before Differentiation Division Working with fractions Adding Subtracting Multiplication

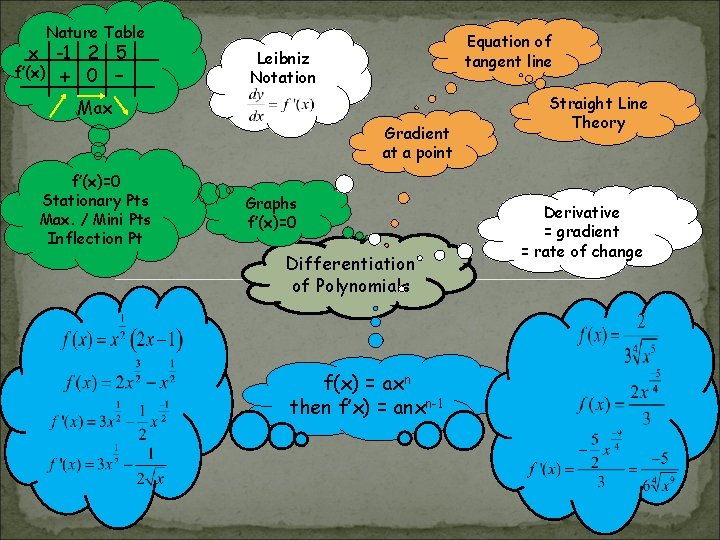
Nature Table x -1 2 5 f’(x) + 0 - Equation of tangent line Leibniz Notation Max Gradient at a point f’(x)=0 Stationary Pts Max. / Mini Pts Inflection Pt Graphs f’(x)=0 Differentiation of Polynomials f(x) = axn then f’x) = anxn-1 Straight Line Theory Derivative = gradient = rate of change

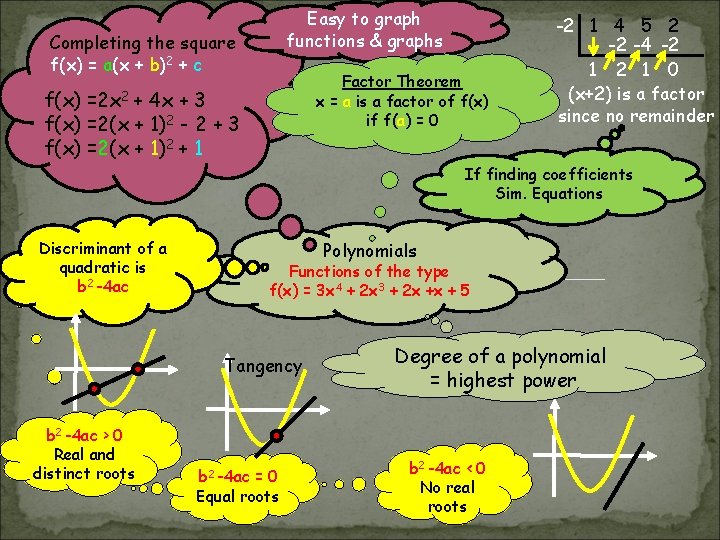
Easy to graph functions & graphs Completing the square f(x) = a(x + b)2 + c Factor Theorem x = a is a factor of f(x) if f(a) = 0 f(x) =2 x 2 + 4 x + 3 f(x) =2(x + 1)2 - 2 + 3 f(x) =2(x + 1)2 + 1 -2 1 4 5 2 -2 -4 -2 1 0 (x+2) is a factor since no remainder If finding coefficients Sim. Equations Discriminant of a quadratic is b 2 -4 ac Polynomials Functions of the type f(x) = 3 x 4 + 2 x 3 + 2 x +x + 5 Tangency b 2 -4 ac > 0 Real and distinct roots b 2 -4 ac = 0 Equal roots Degree of a polynomial = highest power b 2 -4 ac < 0 No real roots

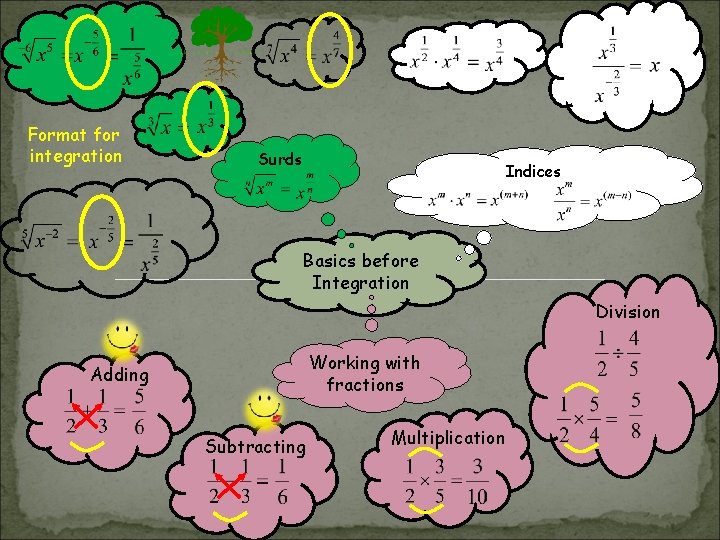
Format for integration Surds Indices Basics before Integration Division Working with fractions Adding Subtracting Multiplication

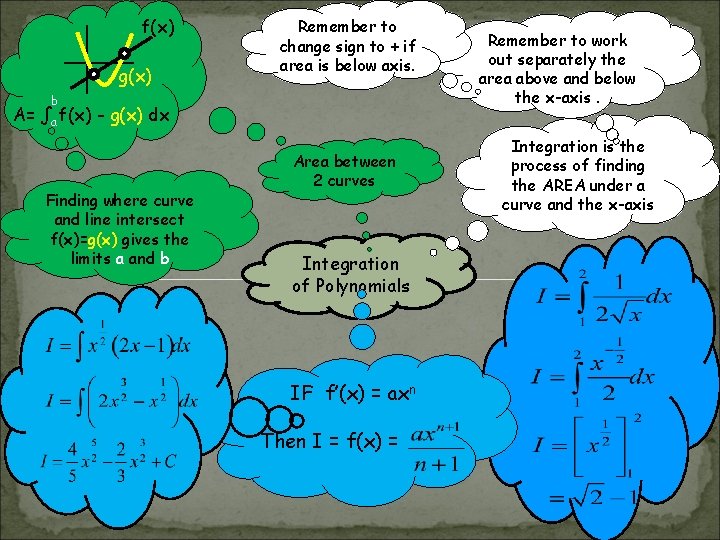
f(x) g(x) Remember to change sign to + if area is below axis. b A= ∫a f(x) - g(x) dx Finding where curve and line intersect f(x)=g(x) gives the limits a and b Area between 2 curves Integration of Polynomials IF f’(x) = axn Then I = f(x) = Remember to work out separately the area above and below the x-axis. Integration is the process of finding the AREA under a curve and the x-axis

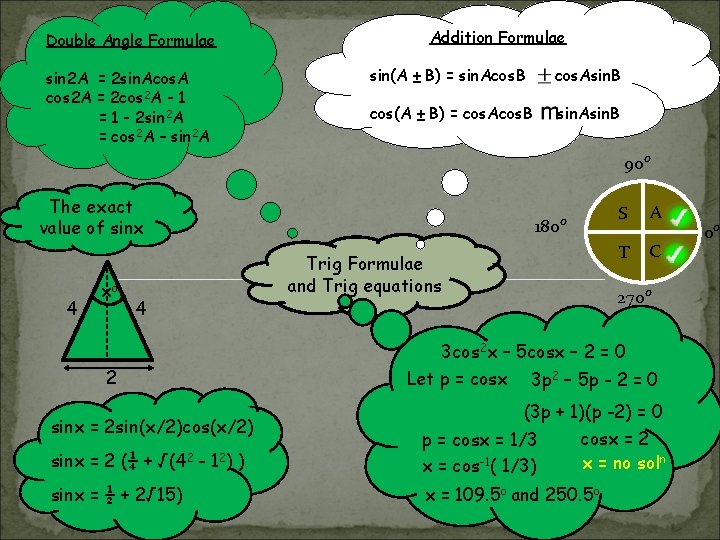
Double Angle Formulae sin 2 A = 2 sin. Acos. A cos 2 A = 2 cos 2 A - 1 = 1 - 2 sin 2 A = cos 2 A – sin 2 A Addition Formulae sin(A ± B) = sin. Acos. B cos. Asin. B cos(A ± B) = cos. Acos. B sin. Asin. B 90 o The exact value of sinx 4 xo 4 2 180 o Trig Formulae and Trig equations S A T C 270 o 3 cos 2 x – 5 cosx – 2 = 0 Let p = cosx 3 p 2 – 5 p - 2 = 0 sinx = 2 (¼ + √(42 - 12) ) (3 p + 1)(p -2) = 0 cosx = 2 p = cosx = 1/3 x = no soln x = cos-1( 1/3) sinx = ½ + 2√ 15) x = 109. 5 o and 250. 5 o sinx = 2 sin(x/2)cos(x/2) 0 o

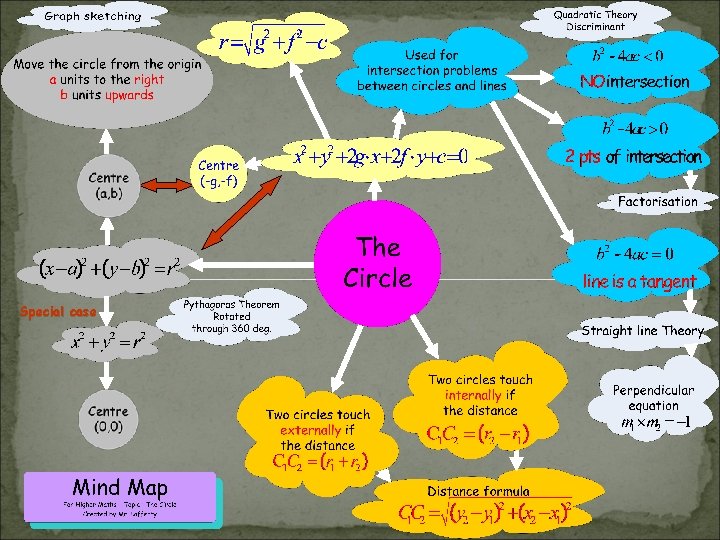
Special case

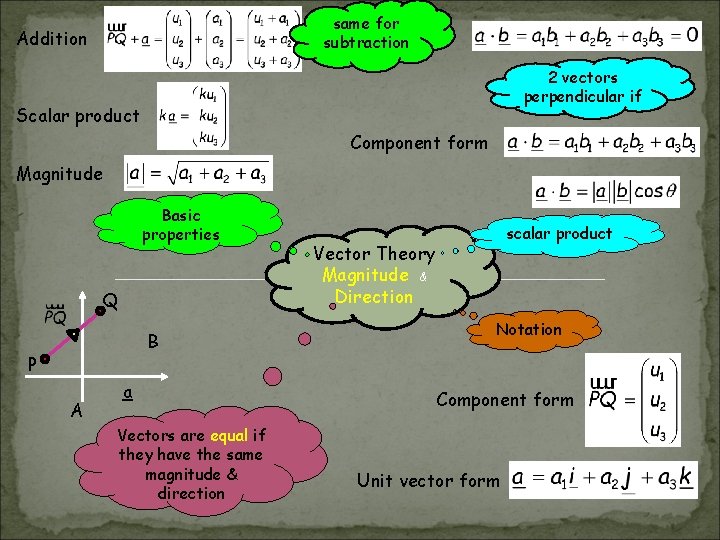
same for subtraction Addition 2 vectors perpendicular if Scalar product Component form Magnitude Basic properties Q B P A a Vectors are equal if they have the same magnitude & direction scalar product Vector Theory Magnitude & Direction Notation Component form Unit vector form

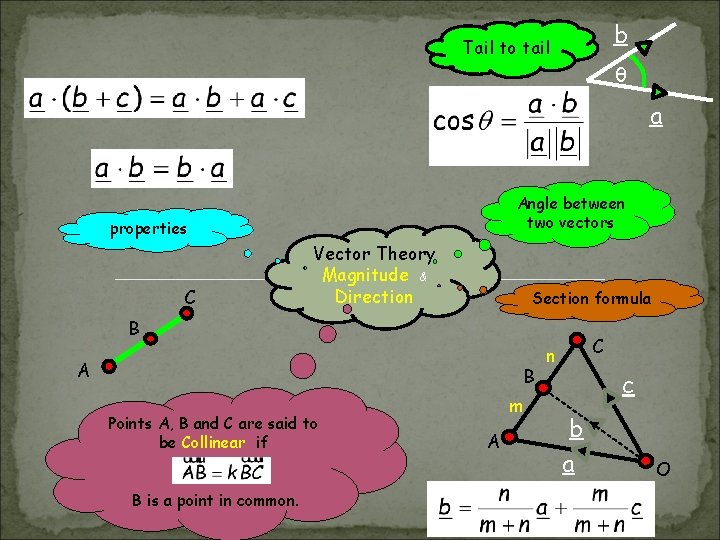
b Tail to tail θ a Angle between two vectors properties C Vector Theory Magnitude & Direction Section formula B A B Points A, B and C are said to be Collinear if B is a point in common. m A C n c b a O

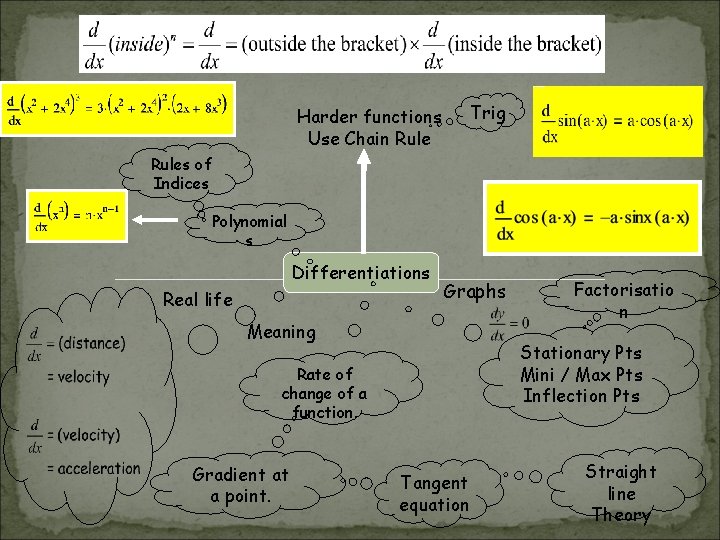
Trig Harder functions Use Chain Rules of Indices Polynomial s Differentiations Real life Graphs Meaning Stationary Pts Mini / Max Pts Inflection Pts Rate of change of a function. Gradient at a point. Factorisatio n Tangent equation Straight line Theory

y y = logax (a, 1) To undo log take exponential loga 1 = 0 logaa = 1 (1, 0) x log A + log B = log AB To undo exponential take log Basic log graph Basic exponential graph y = axb abx Can be transformed into a graph of the form log y = x log b + log a (0, C) x a 0 = 1 a 1 = a Logs & Exponentials Basic log rules log y (1, a) x log A - log B = log A B n log (A) = n log A y= y (0, 1) y = ax Y = m. X + C Y = (log b) X + C C = log a m = log b log y = b log x + log a Y = m. X + C Y = b. X + C C = log a m=b log y (0, C) log x

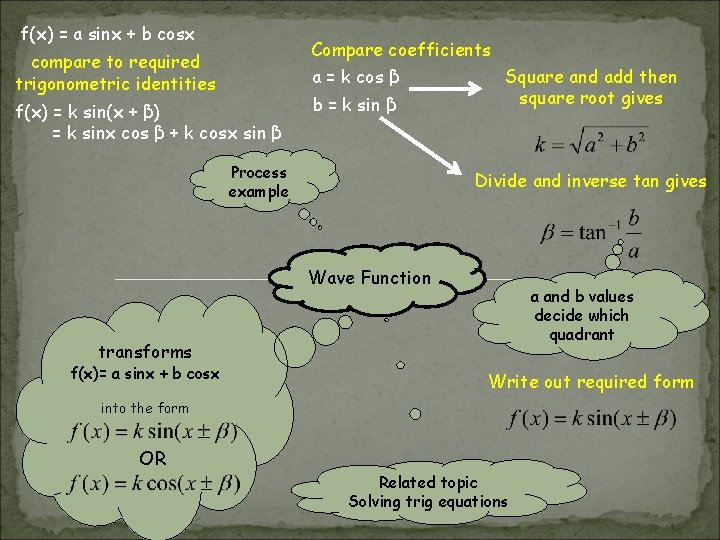
f(x) = a sinx + b cosx Compare coefficients compare to required trigonometric identities a = k cos β f(x) = k sin(x + β) = k sinx cos β + k cosx sin β b = k sin β Process example Square and add then square root gives Divide and inverse tan gives Wave Function a and b values decide which quadrant transforms f(x)= a sinx + b cosx Write out required form into the form OR Related topic Solving trig equations