Higher Physics Electricity Electricity Contents Monitoring and measuring

Higher Physics Electricity

Electricity: Contents Monitoring and measuring a. c. Current, p. d. , power and resistance Electrical sources and internal resistance. Capacitors Conductors, semiconductors and insulators p-n junctions

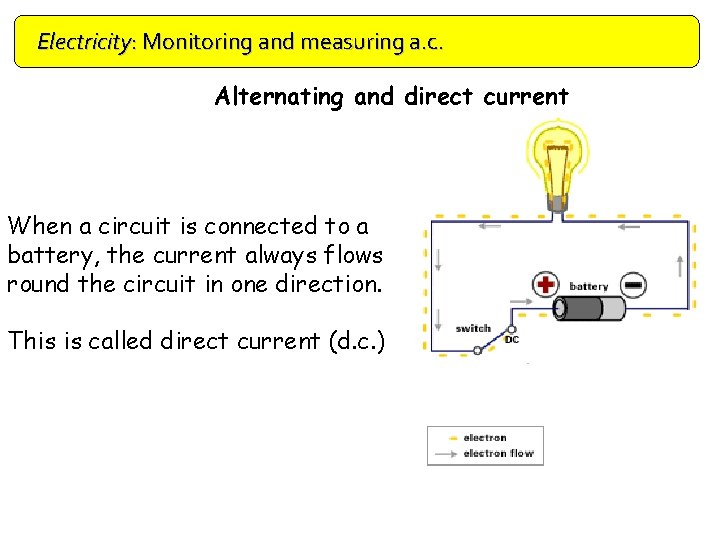
Electricity: Monitoring and measuring a. c. Alternating and direct current When a circuit is connected to a battery, the current always flows round the circuit in one direction. This is called direct current (d. c. )

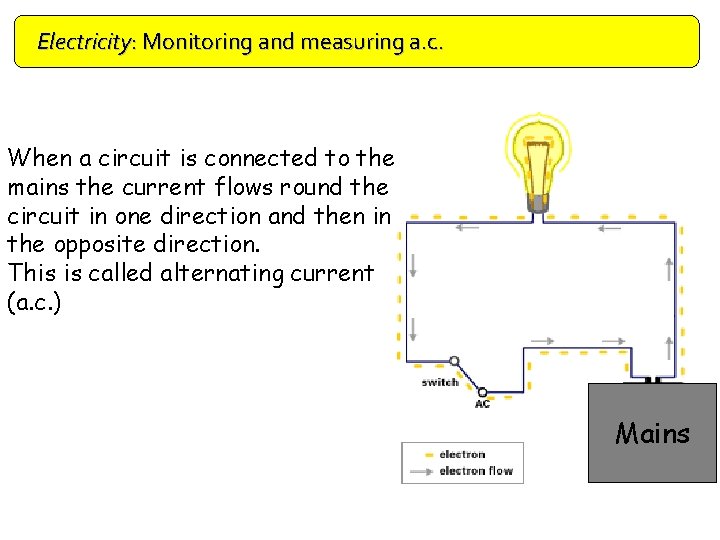
Electricity: Monitoring and measuring a. c. When a circuit is connected to the mains the current flows round the circuit in one direction and then in the opposite direction. This is called alternating current (a. c. ) Mains

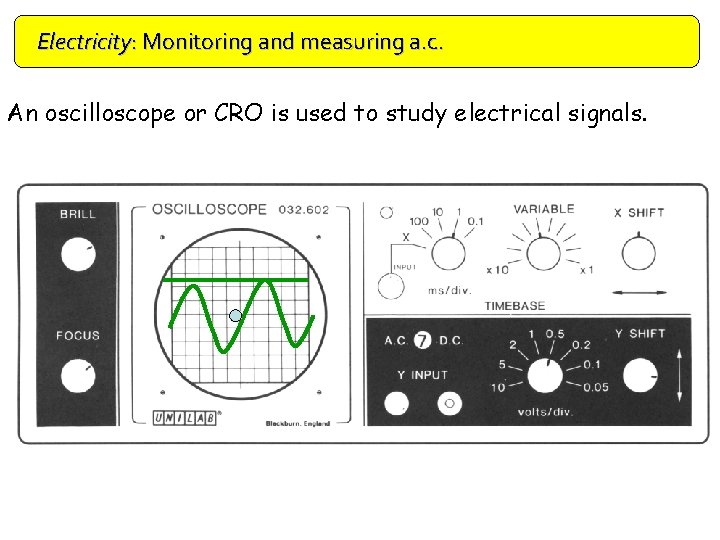
Electricity: Monitoring and measuring a. c. An oscilloscope or CRO is used to study electrical signals.

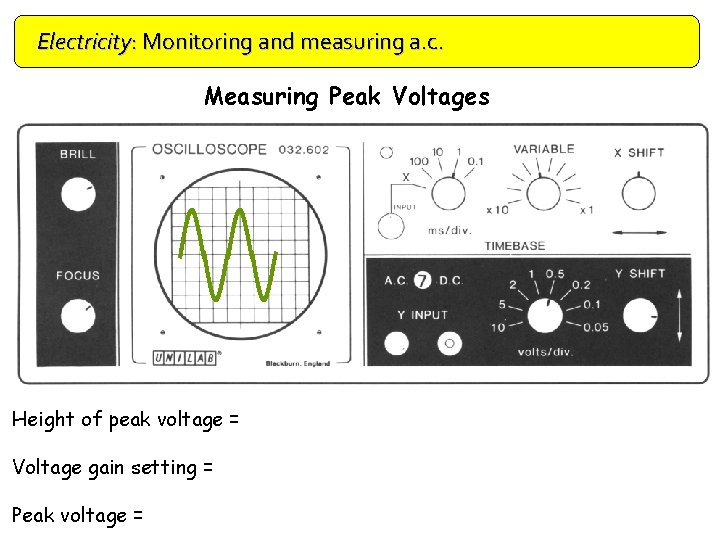
Electricity: Monitoring and measuring a. c. Measuring Peak Voltages Height of peak voltage = Voltage gain setting = Peak voltage =

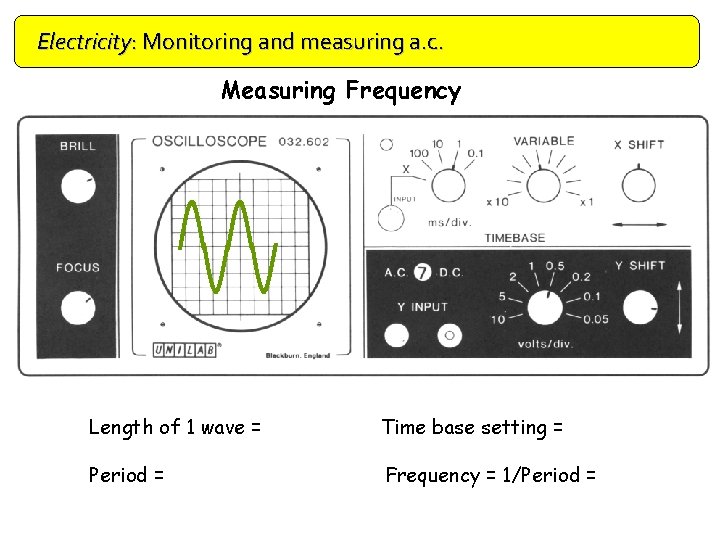
Electricity: Monitoring and measuring a. c. Measuring Frequency Length of 1 wave = Time base setting = Period = Frequency = 1/Period =

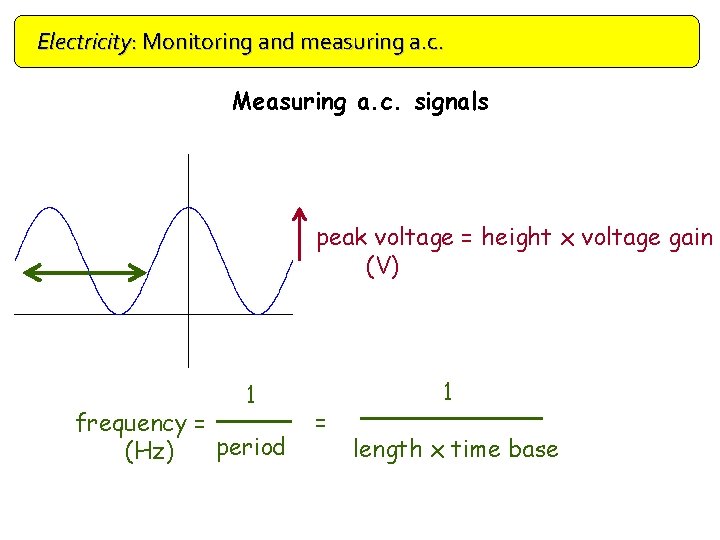
Electricity: Monitoring and measuring a. c. Measuring a. c. signals peak voltage = height x voltage gain (V) 1 frequency = period (Hz) = 1 length x time base

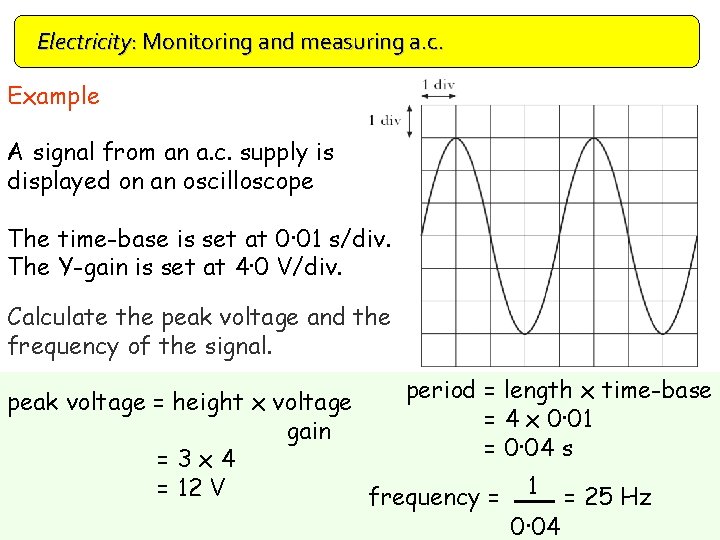
Electricity: Monitoring and measuring a. c. Example A signal from an a. c. supply is displayed on an oscilloscope The time-base is set at 0· 01 s/div. The Y-gain is set at 4· 0 V/div. Calculate the peak voltage and the frequency of the signal. period = length x time-base peak voltage = height x voltage = 4 x 0· 01 gain = 0· 04 s =3 x 4 = 12 V frequency = 1 = 25 Hz 0· 04

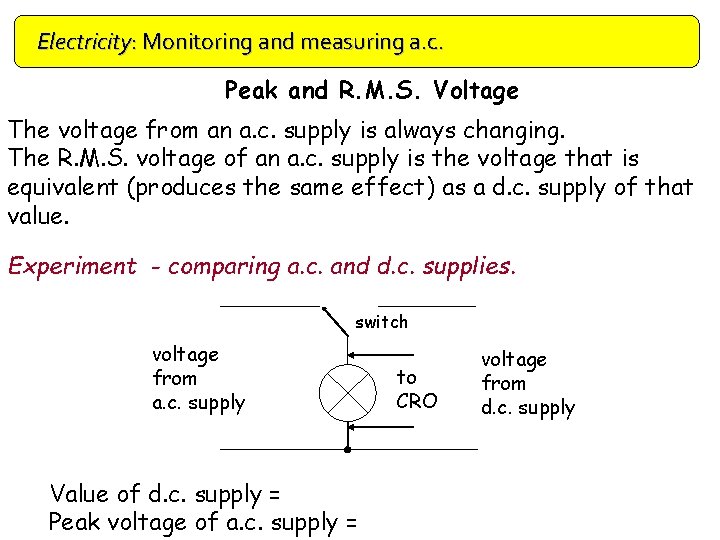
Electricity: Monitoring and measuring a. c. Peak and R. M. S. Voltage The voltage from an a. c. supply is always changing. The R. M. S. voltage of an a. c. supply is the voltage that is equivalent (produces the same effect) as a d. c. supply of that value. Experiment - comparing a. c. and d. c. supplies. switch voltage from a. c. supply Value of d. c. supply = Peak voltage of a. c. supply = to CRO voltage from d. c. supply

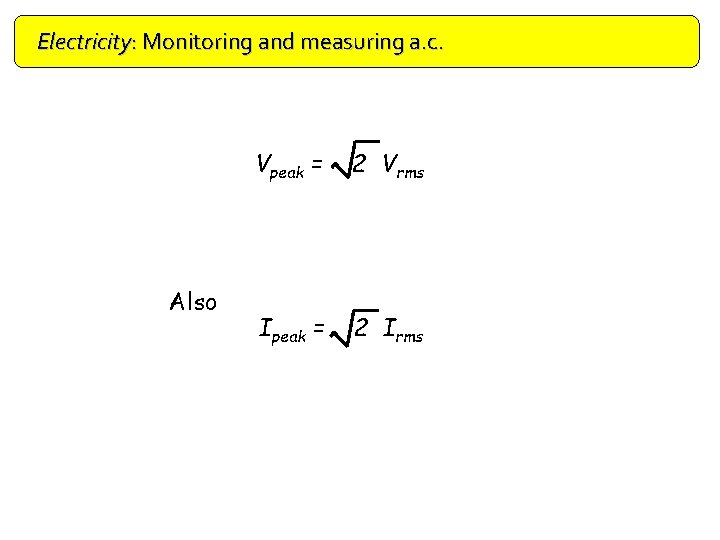
Electricity: Monitoring and measuring a. c. Also Vpeak = 2 Vrms Ipeak = 2 Irms

Electricity: Monitoring and measuring a. c. Example The r. m. s. voltage from an a. c. supply is 6 V. Calculate the peak voltage. Vpeak = 2 Vrms = 2 x 6 = 8· 5 V

Electricity: Current, p. d. , power and resistance. Charge, Current and Time An electrical current is a flow of (negative) charge around a circuit. The amount of charge that flows around a circuit depends on the size of the current and the time the charge flows. current in amperes (A) Q=It time in seconds (s) charge in coulombs (C)

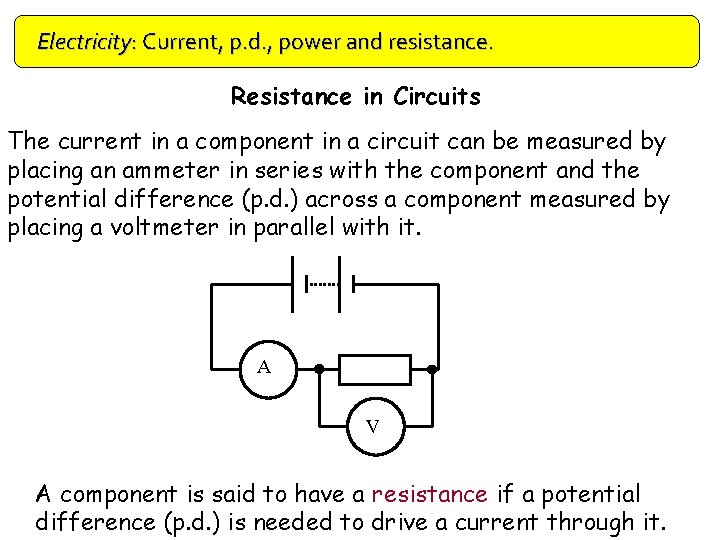
Electricity: Current, p. d. , power and resistance. Resistance in Circuits The current in a component in a circuit can be measured by placing an ammeter in series with the component and the potential difference (p. d. ) across a component measured by placing a voltmeter in parallel with it. A V A component is said to have a resistance if a potential difference (p. d. ) is needed to drive a current through it.

Electricity: Current, p. d. , power and resistance. Experiment – Ohm’s Law Aim : To find the relationship between the current in a resistor and the p. d. across it. p. d. (V) current (A)

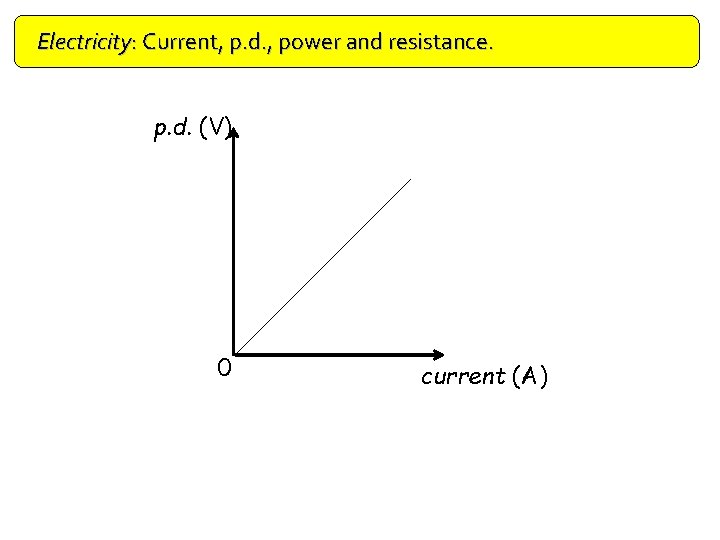
Electricity: Current, p. d. , power and resistance. p. d. (V) 0 current (A)

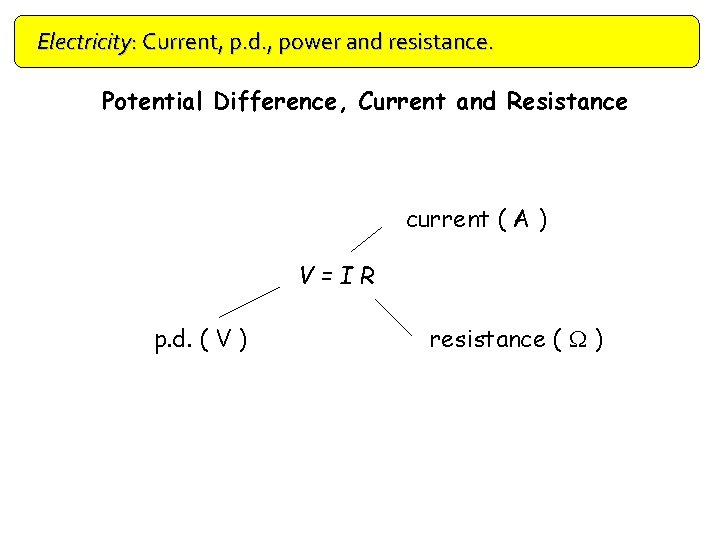
Electricity: Current, p. d. , power and resistance. Potential Difference, Current and Resistance current ( A ) V=IR p. d. ( V ) resistance ( W )

Electricity: Current, p. d. , power and resistance. Example What is the potential difference across a 2· 0 W resistor if the current through the resistor is 5· 0 A? V = IR =5 x 2 = 10 V

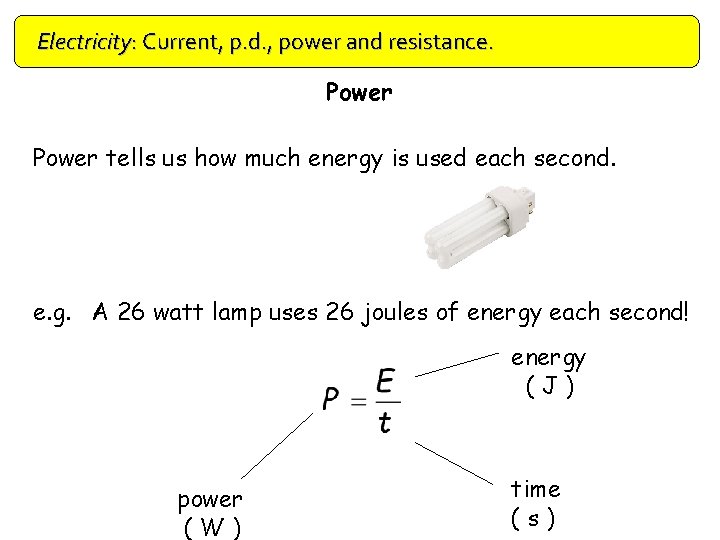
Electricity: Current, p. d. , power and resistance. Power tells us how much energy is used each second. e. g. A 26 watt lamp uses 26 joules of energy each second! energy (J) power (W) time (s)

Electricity: Current, p. d. , power and resistance. If the current through a component is I and the potential difference across a component is V, then the power is given by P = I V. Experiment Aim: To find the power rating of lamps Lamp rating (W) Voltage (V) Current (A) Current x Voltage

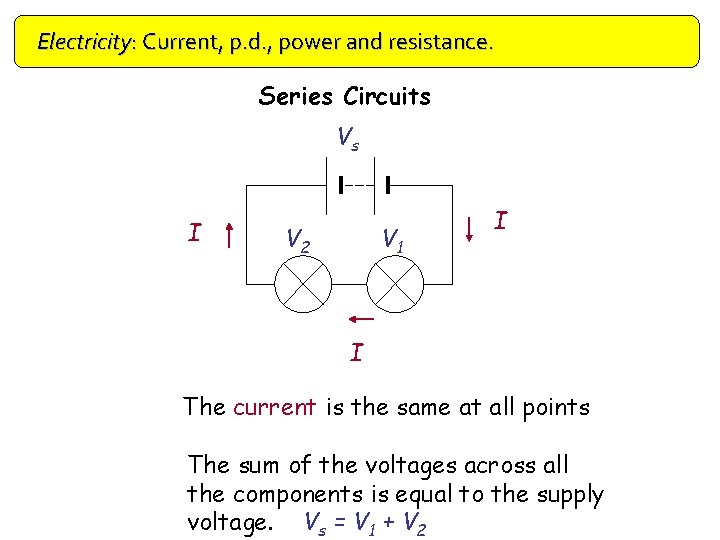
Electricity: Current, p. d. , power and resistance. Series Circuits Vs I V 2 V 1 I I The current is the same at all points The sum of the voltages across all the components is equal to the supply voltage. Vs = V 1 + V 2

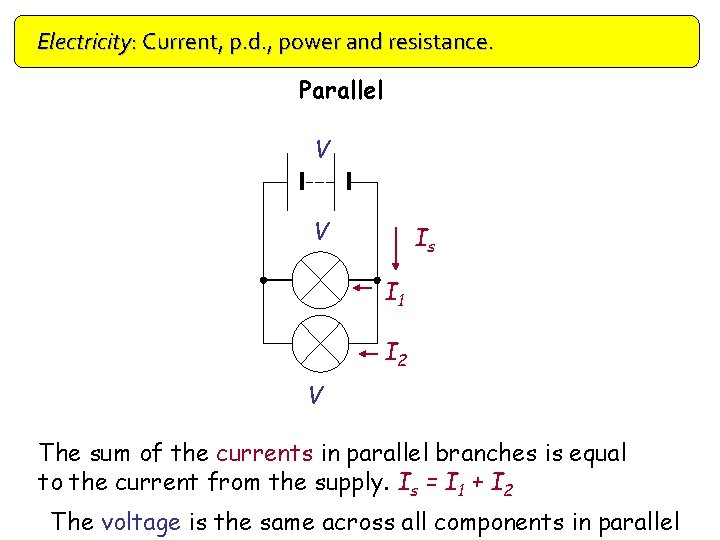
Electricity: Current, p. d. , power and resistance. Parallel V V Is I 1 I 2 V The sum of the currents in parallel branches is equal to the current from the supply. Is = I 1 + I 2 The voltage is the same across all components in parallel

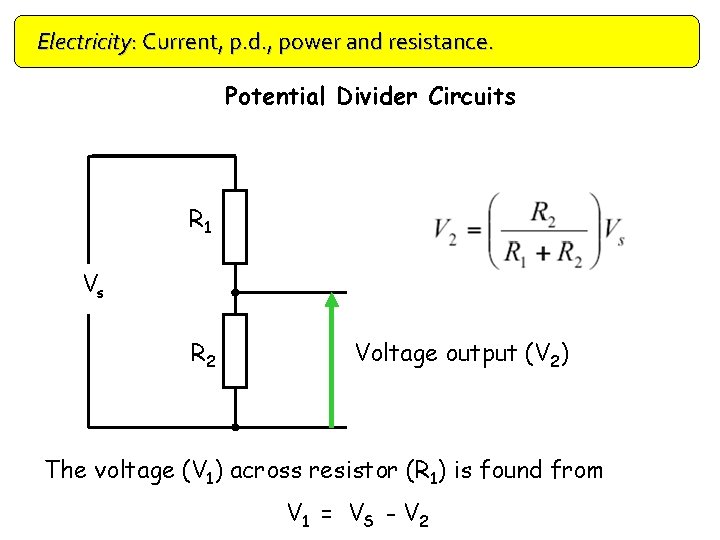
Electricity: Current, p. d. , power and resistance. Potential Divider Circuits R 1 Vs R 2 Voltage output (V 2) The voltage (V 1) across resistor (R 1) is found from V 1 = V S - V 2

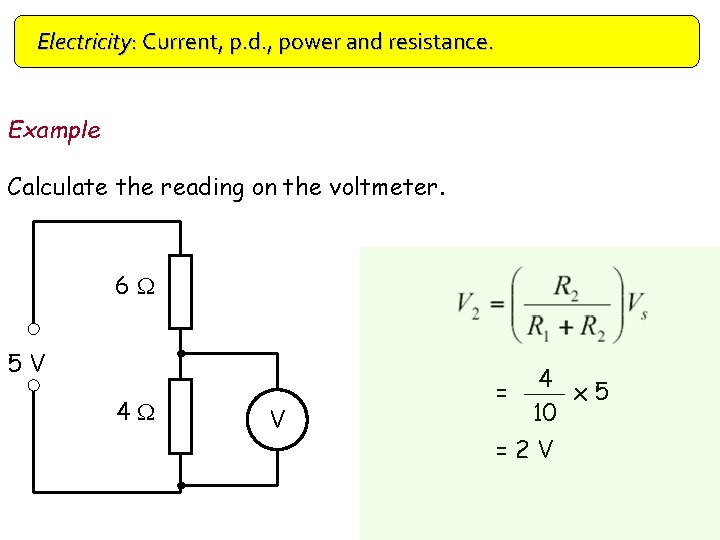
Electricity: Current, p. d. , power and resistance. Example Calculate the reading on the voltmeter. 6 W 5 V 4 W V 4 = x 5 10 =2 V

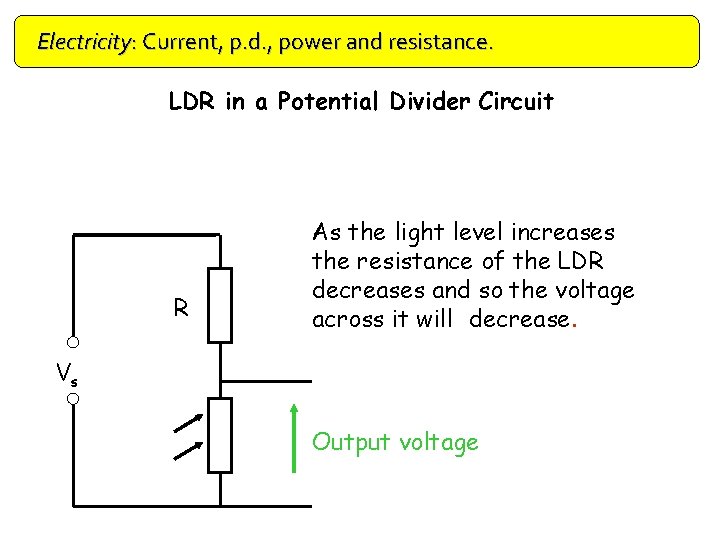
Electricity: Current, p. d. , power and resistance. LDR in a Potential Divider Circuit R As the light level increases the resistance of the LDR decreases and so the voltage across it will decrease. Vs Output voltage

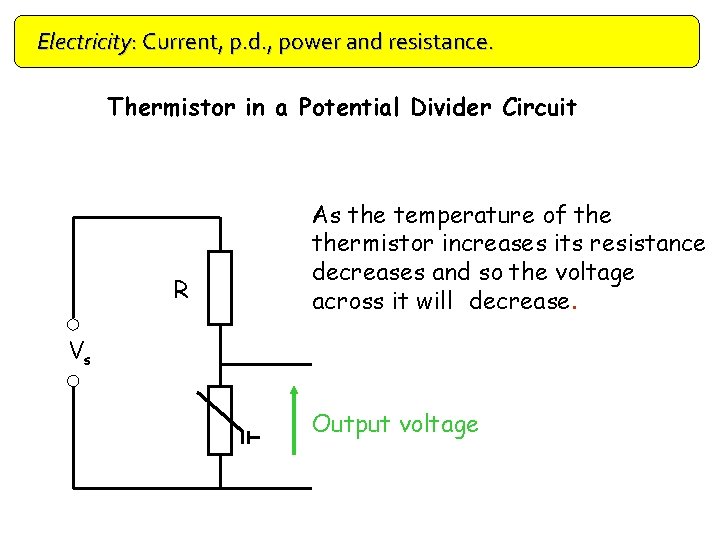
Electricity: Current, p. d. , power and resistance. Thermistor in a Potential Divider Circuit R As the temperature of thermistor increases its resistance decreases and so the voltage across it will decrease. Vs Output voltage

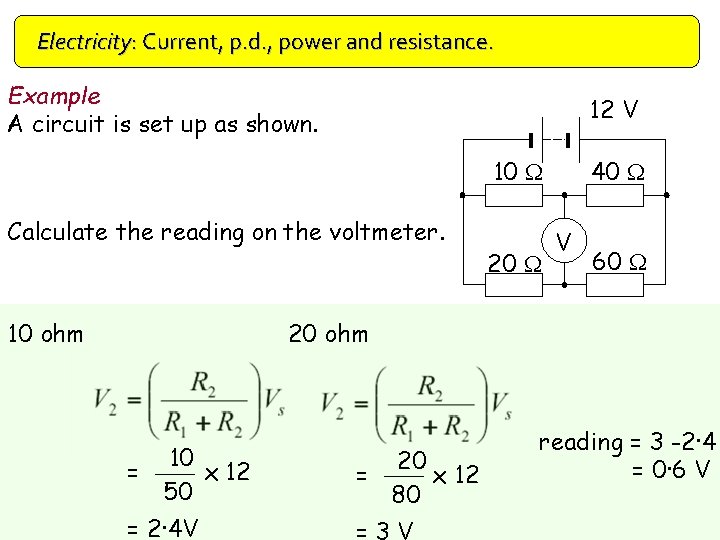
Electricity: Current, p. d. , power and resistance. Example A circuit is set up as shown. 12 V 10 W Calculate the reading on the voltmeter. 10 ohm 20 W 40 W V 60 W 20 ohm = 10 x 12 50 = 2· 4 V = 20 x 12 80 reading = 3 -2· 4 = 0· 6 V

Electricity: Electrical sources and internal resistance E. M. F. A battery provides an electromotive force (e. m. f. ) to drive current around a circuit. The e. m. f is defined as the electrical energy supplied to each coulomb of charge that passes through the battery. The units of e. m. f are the same as p. d. 1 JC-1 = 1 V The e. m. f. of a battery can be measured using a voltmeter to find the p. d. across the terminals of the battery when no current is flowing (open circuit).

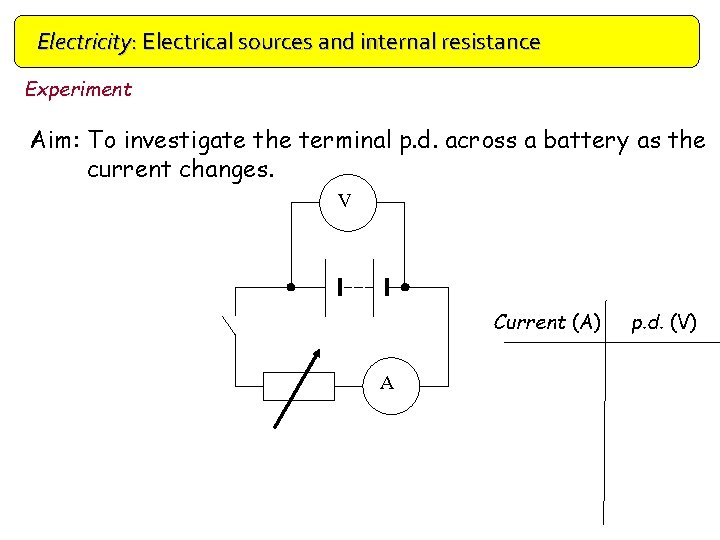
Electricity: Electrical sources and internal resistance Experiment Aim: To investigate the terminal p. d. across a battery as the current changes. V Current (A) A p. d. (V)

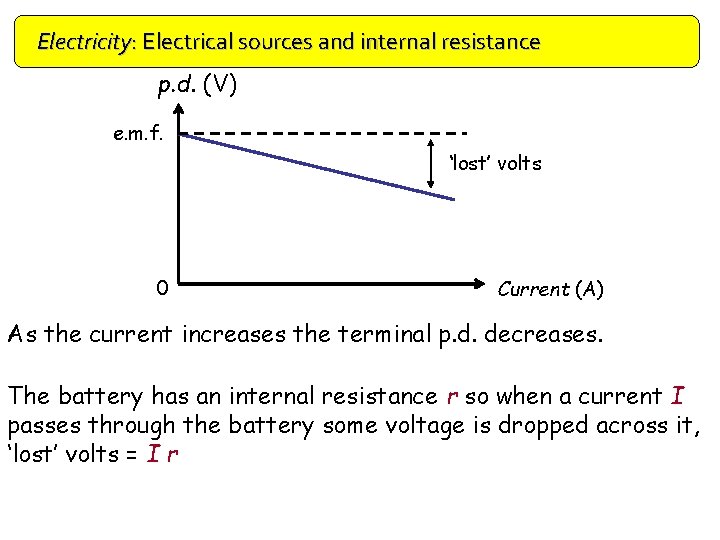
Electricity: Electrical sources and internal resistance p. d. (V) e. m. f. ‘lost’ volts 0 Current (A) As the current increases the terminal p. d. decreases. The battery has an internal resistance r so when a current I passes through the battery some voltage is dropped across it, ‘lost’ volts = I r

Electricity: Electrical sources and internal resistance The terminal p. d. will always be less than the e. m. f. when a current flows. E=V+Ir e. m. f. ( V ) terminal p. d. (V) internal resistance (W) current (A)

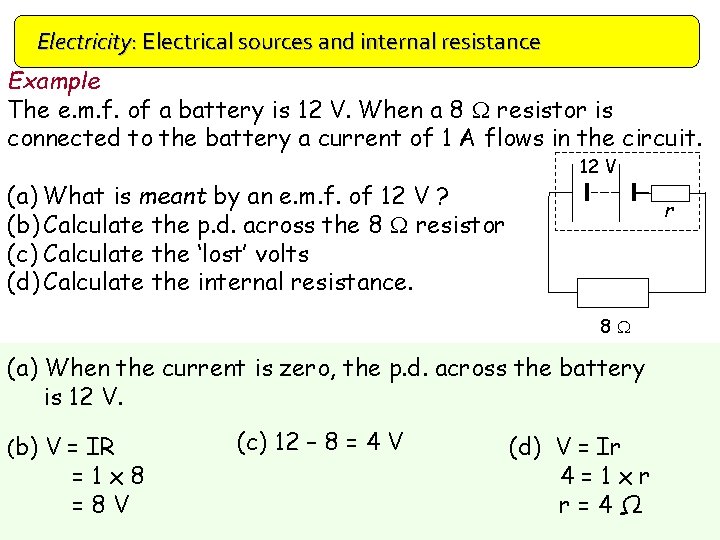
Electricity: Electrical sources and internal resistance Example The e. m. f. of a battery is 12 V. When a 8 W resistor is connected to the battery a current of 1 A flows in the circuit. (a) What is meant by an e. m. f. of 12 V ? (b) Calculate the p. d. across the 8 W resistor (c) Calculate the ‘lost’ volts (d) Calculate the internal resistance. 12 V r 8 W (a) When the current is zero, the p. d. across the battery is 12 V. (b) V = IR =1 x 8 =8 V (c) 12 – 8 = 4 V (d) V = Ir 4=1 xr r=4Ω

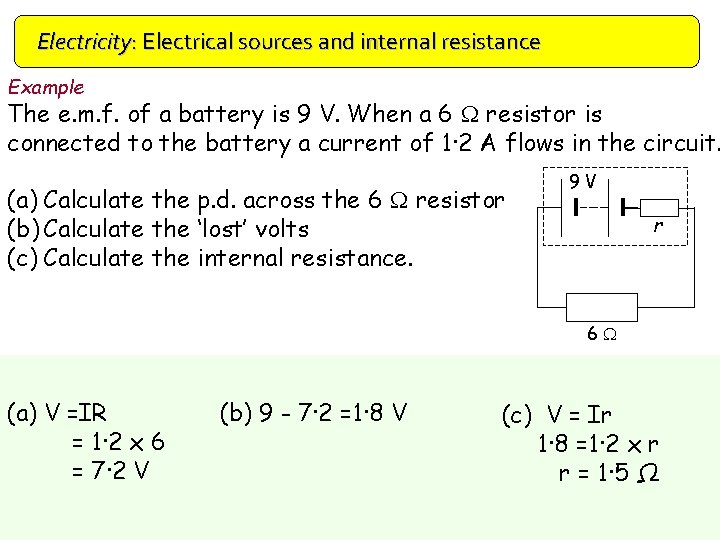
Electricity: Electrical sources and internal resistance Example The e. m. f. of a battery is 9 V. When a 6 W resistor is connected to the battery a current of 1· 2 A flows in the circuit. (a) Calculate the p. d. across the 6 W resistor (b) Calculate the ‘lost’ volts (c) Calculate the internal resistance. 9 V r 6 W (a) V =IR = 1· 2 x 6 = 7· 2 V (b) 9 - 7· 2 =1· 8 V (c) V = Ir 1· 8 =1· 2 x r r = 1· 5 Ω

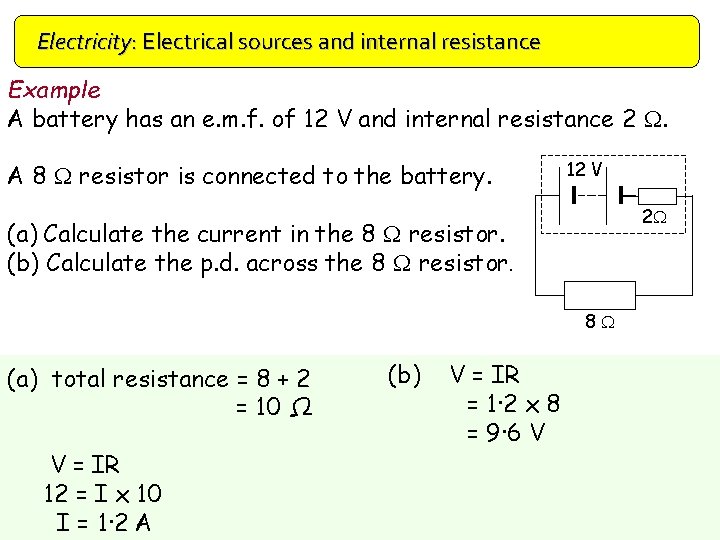
Electricity: Electrical sources and internal resistance Example A battery has an e. m. f. of 12 V and internal resistance 2 W. A 8 W resistor is connected to the battery. 12 V 2 W (a) Calculate the current in the 8 W resistor. (b) Calculate the p. d. across the 8 W resistor. 8 W (a) total resistance = 8 + 2 = 10 Ω V = IR 12 = I x 10 I = 1· 2 A (b) V = IR = 1· 2 x 8 = 9· 6 V

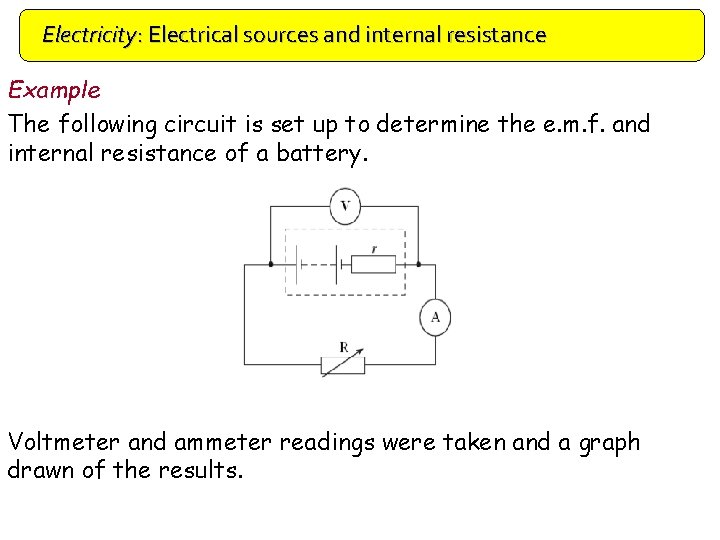
Electricity: Electrical sources and internal resistance Example The following circuit is set up to determine the e. m. f. and internal resistance of a battery. Voltmeter and ammeter readings were taken and a graph drawn of the results.

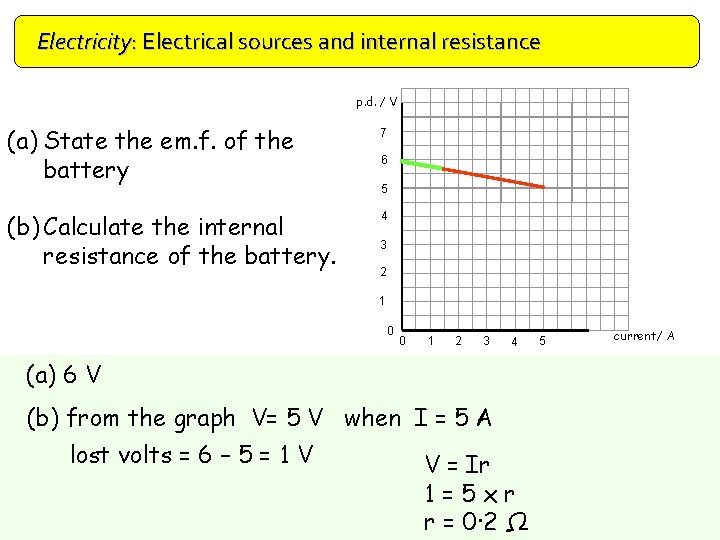
Electricity: Electrical sources and internal resistance p. d. / V (a) State the em. f. of the battery 7 (b) Calculate the internal resistance of the battery. 4 6 5 3 2 1 0 0 1 2 3 4 (a) 6 V (b) from the graph V= 5 V when I = 5 A lost volts = 6 – 5 = 1 V V = Ir 1=5 xr r = 0· 2 Ω 5 current/ A

E is the emf, the p. d. across the battery when no current flows in the circuit. E r R is the external resistance (load resistor) r is the internal resistance Terminal p. d. is the voltage across R Lost volts is the voltage across r I can be calculated several ways: I = lost volts ÷ r I = E ÷ (R + r) I = terminal p. d. ÷ R R

power matching

Electricity: Capacitors A capacitor is a device designed to store charge. Circuit symbol

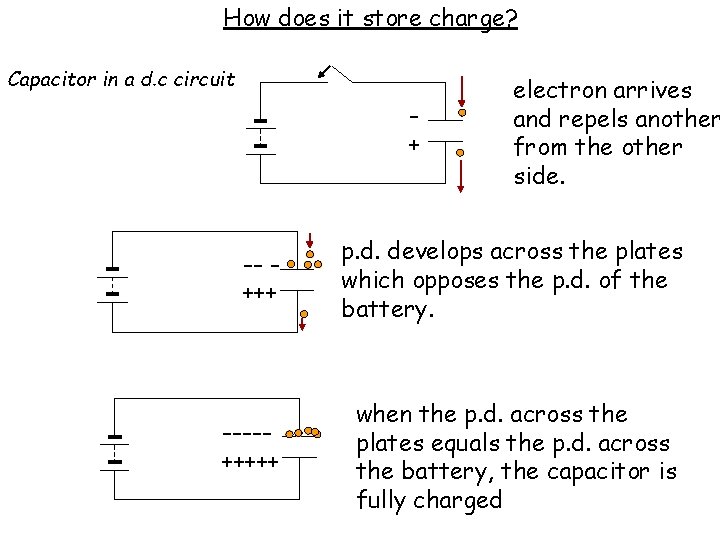
How does it store charge? Capacitor in a d. c circuit + electron arrives and repels another from the other side. -- +++ p. d. develops across the plates which opposes the p. d. of the battery. ----+++++ when the p. d. across the plates equals the p. d. across the battery, the capacitor is fully charged

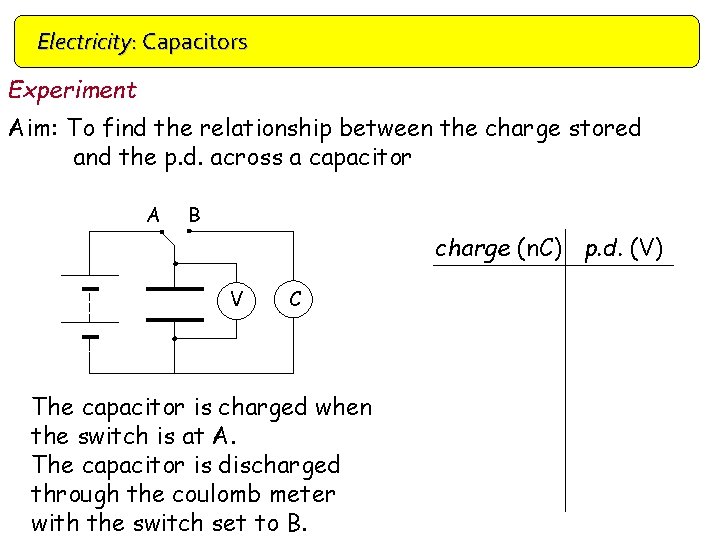
Electricity: Capacitors Experiment Aim: To find the relationship between the charge stored and the p. d. across a capacitor A B charge (n. C) p. d. (V) V C The capacitor is charged when the switch is at A. The capacitor is discharged through the coulomb meter with the switch set to B.

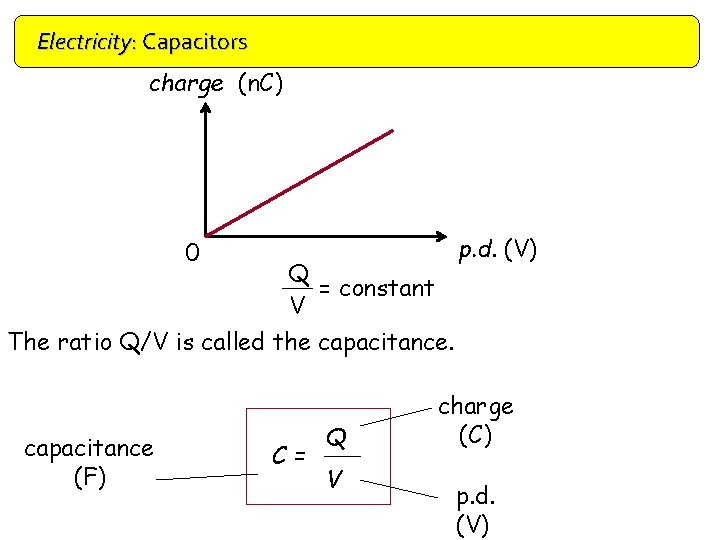
Electricity: Capacitors charge (n. C) 0 Q = constant V The ratio Q/V is called the capacitance (F) C= Q V p. d. (V) charge (C) p. d. (V)

Electricity: Capacitors Example Calculate the charge stored in a 2000 m. F capacitor when the p. d. across the capacitor is 12 V. C= 2000 x 10 -6 = Q V Q 12 Q = 0· 024 C

Electricity: Capacitors The Energy Stored in a Capacitor Charge (C) p. d. (V) 0 The energy stored in a capacitor is given by the area under the charge/voltage graph. Energy (J) E= 1 QV 2 Potential Difference (V) Charge (C)

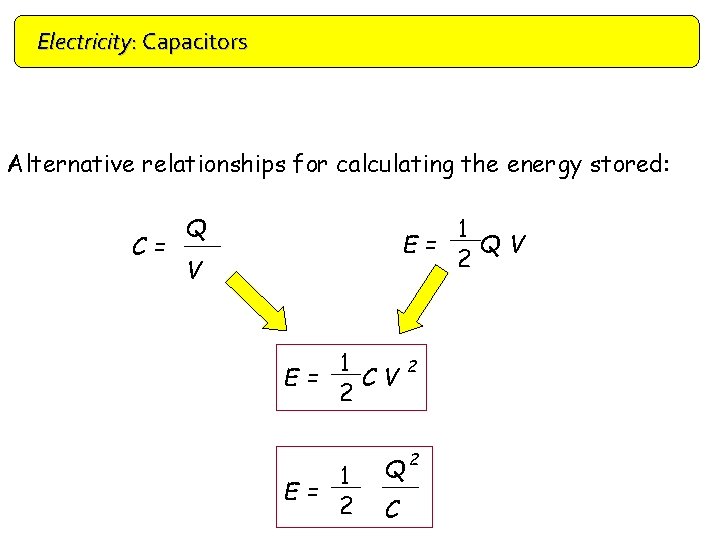
Electricity: Capacitors Alternative relationships for calculating the energy stored: C= Q 1 E= QV 2 V 1 E= CV 2 1 E= 2 Q C 2 2

Electricity: Capacitors Example The p. d. across a 2000 μF capacitor is 12 V. Calculate the energy stored in the capacitor. E= 1 CV 2 2 E = 1 2000 x 10 -6 x 122 2 E = 0· 144 J

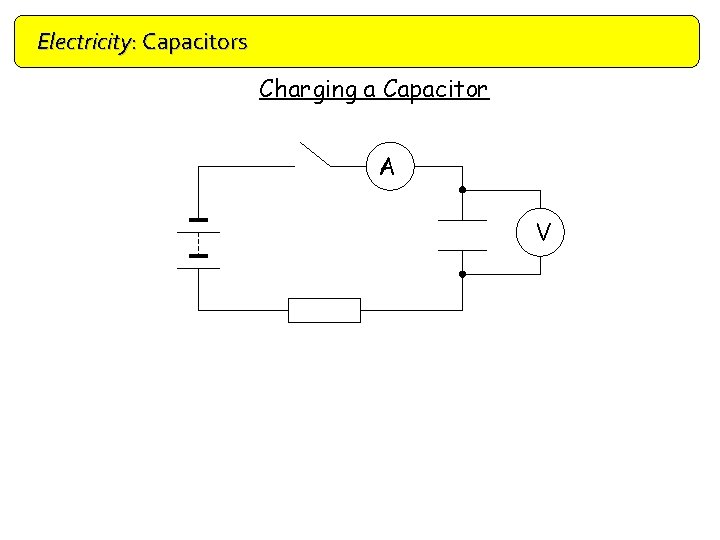
Electricity: Capacitors Charging a Capacitor A V Current/ m. A Time /s P. d. / V Time / s

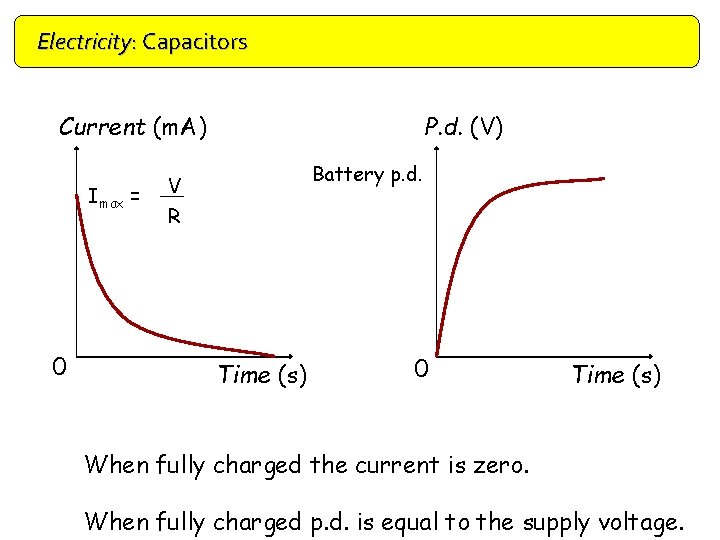
Electricity: Capacitors Current (m. A) Imax = 0 P. d. (V) Battery p. d. V R Time (s) 0 Time (s) When fully charged the current is zero. When fully charged p. d. is equal to the supply voltage.

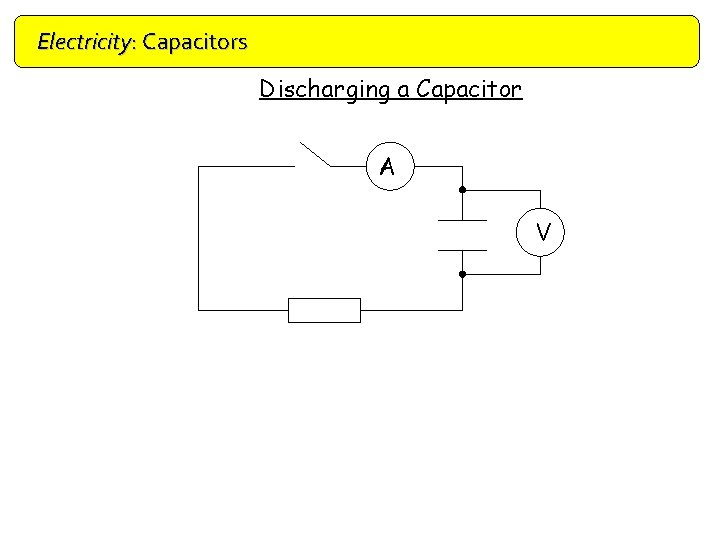
Electricity: Capacitors Discharging a Capacitor A V Current/ m. A Time /s P. d. / V Time / s

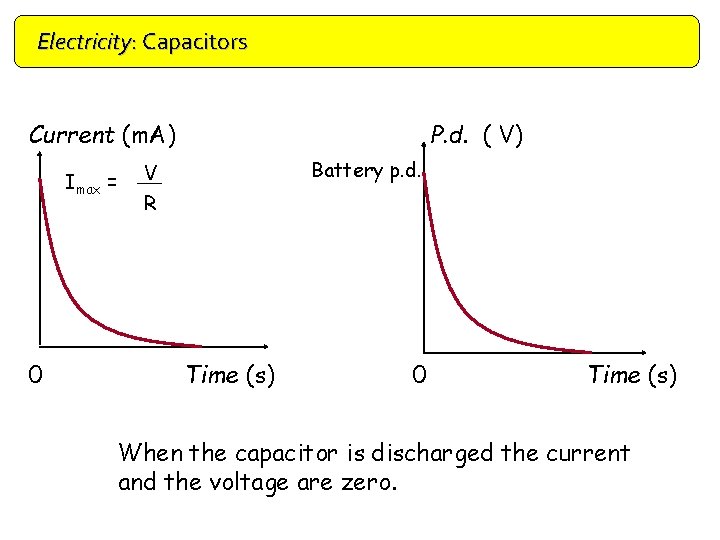
Electricity: Capacitors Current (m. A) Imax = 0 P. d. ( V) Battery p. d. V R Time (s) 0 Time (s) When the capacitor is discharged the current and the voltage are zero.

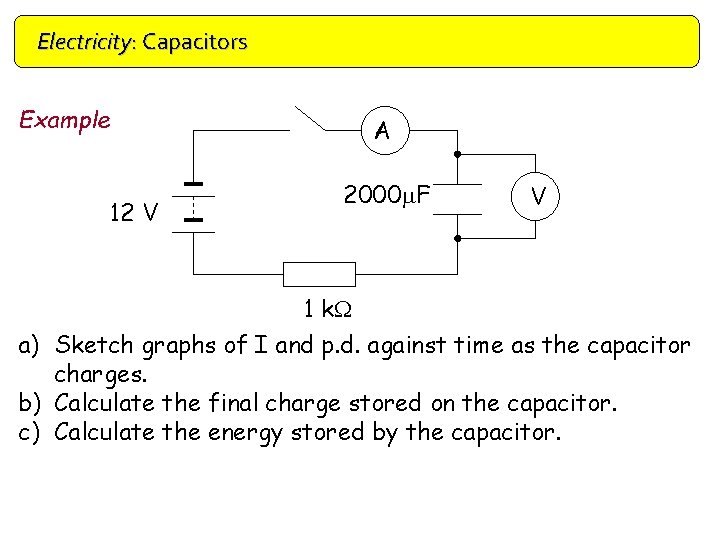
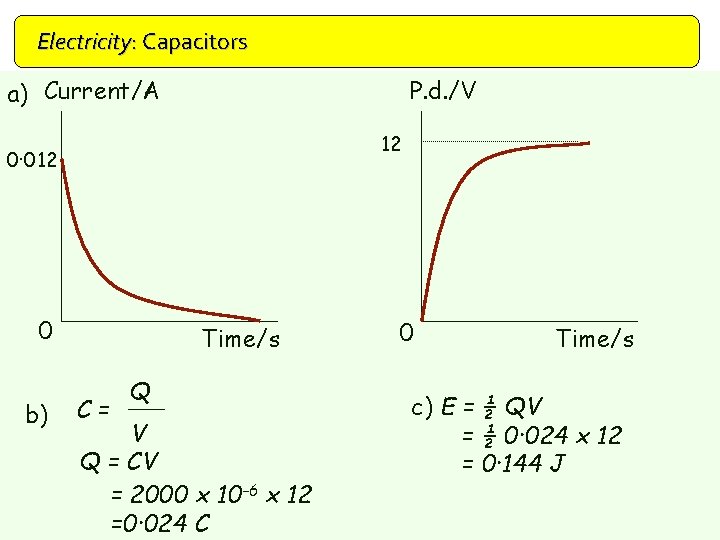
Electricity: Capacitors Example 12 V A 2000 m. F V 1 k. W a) Sketch graphs of I and p. d. against time as the capacitor charges. b) Calculate the final charge stored on the capacitor. c) Calculate the energy stored by the capacitor.

Electricity: Capacitors a) Current/A P. d. /V 12 0· 012 0 b) Time/s C= Q V Q = CV = 2000 x 10 -6 x 12 =0· 024 C 0 Time/s c) E = ½ QV = ½ 0· 024 x 12 = 0· 144 J

Electricity: Electrons at work Doping Conductors, semiconductors and insulators Solids can be categorised into conductors, semiconductors or insulators by their ability to conduct electricity. Examples Conductors: copper, iron, aluminium Insulators : plastic, rubber, glass Semiconductors: silicon, germanium, selenium

Electricity: Electrons at work Doping Band Theory Band theory explains the different electrical properties of conductors, insulators and semiconductors. In an atom, electrons occupy discrete energy levels. When atoms combine to form a solid, the electrons become contained in energy bands separated by gaps. The two highest energy bands are called the valence band the conduction band.

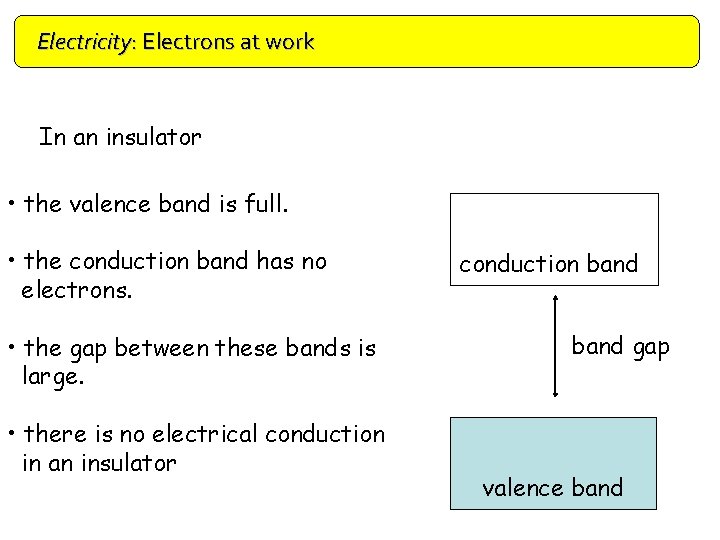
Electricity: Electrons at work Doping In an insulator • the valence band is full. • the conduction band has no electrons. • the gap between these bands is large. • there is no electrical conduction in an insulator conduction band gap valence band

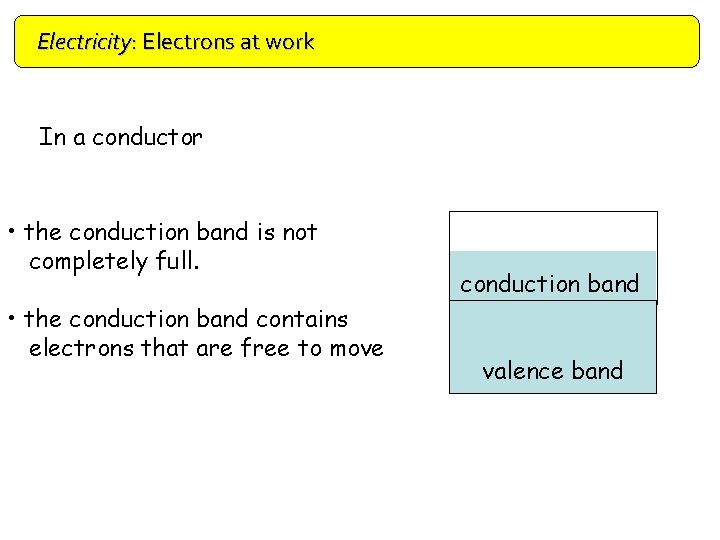
Electricity: Electrons at work Doping In a conductor • the conduction band is not completely full. • the conduction band contains electrons that are free to move conduction band valence band

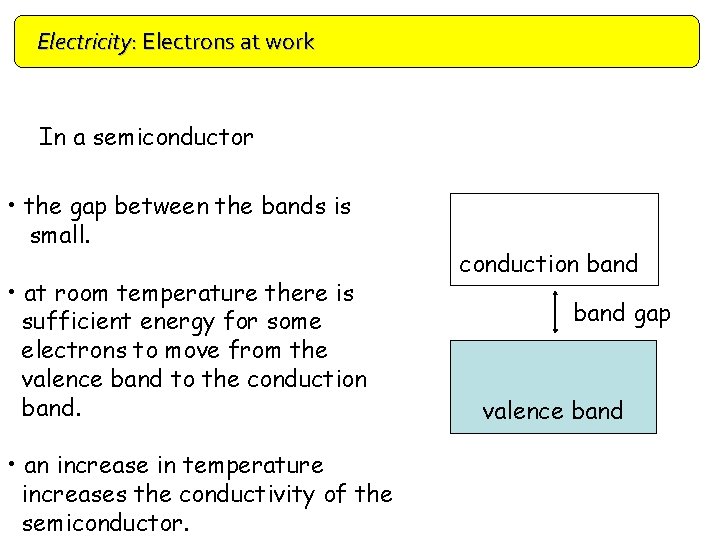
Electricity: Electrons at work Doping In a semiconductor • the gap between the bands is small. • at room temperature there is sufficient energy for some electrons to move from the valence band to the conduction band. • an increase in temperature increases the conductivity of the semiconductor. conduction band gap valence band

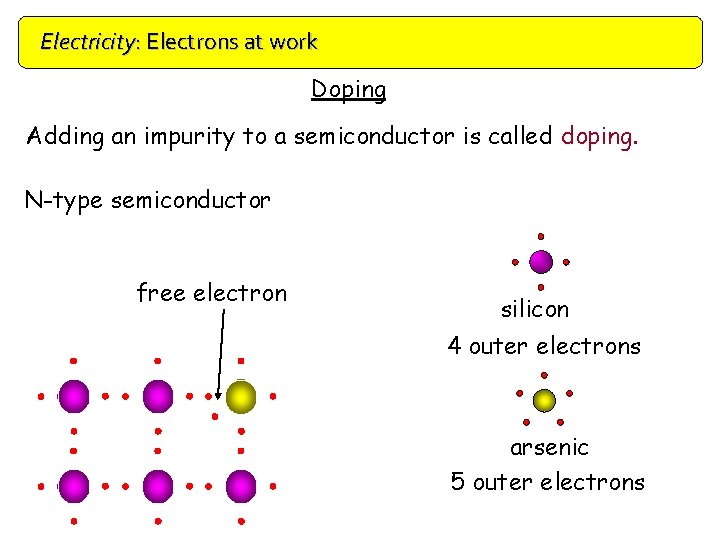
Electricity: Electrons at work Doping Adding an impurity to a semiconductor is called doping. N-type semiconductor free electron silicon 4 outer electrons arsenic 5 outer electrons

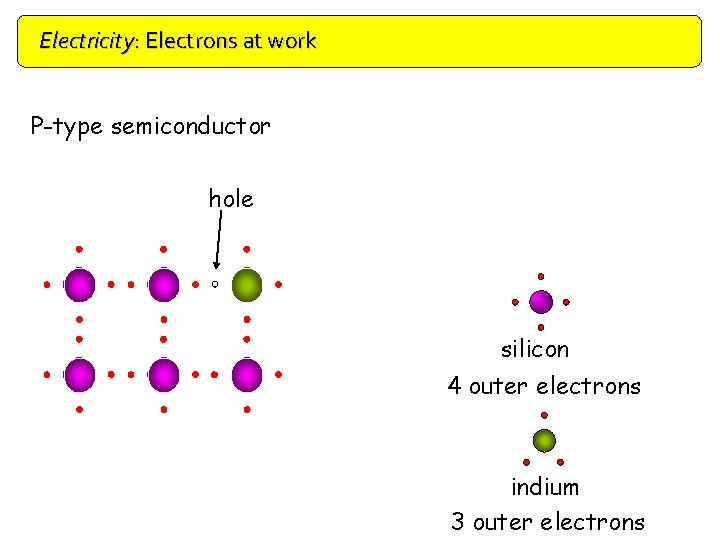
Electricity: Electrons at work Doping P-type semiconductor hole silicon 4 outer electrons indium 3 outer electrons

Electricity: Electrons at work Doping reduces the resistance of a semiconductor. In n-type semiconductors conduction takes place by the movement of free electrons. In p-type semiconductors conduction takes place because electrons can move into the holes where an electron is missing, we say that conduction takes place due to the movement of positive holes.

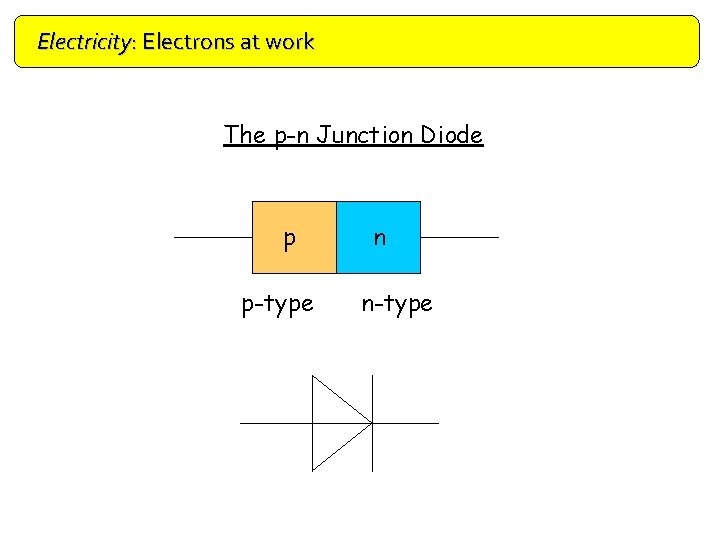
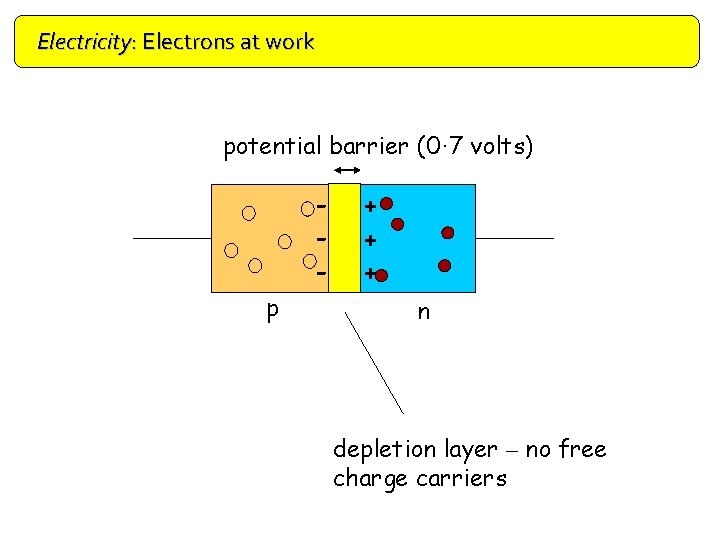
Electricity: Electrons at work Doping The p-n Junction Diode p p-type n n-type

Electricity: Electrons at work Doping potential barrier (0· 7 volts) p + + + n depletion layer – no free charge carriers

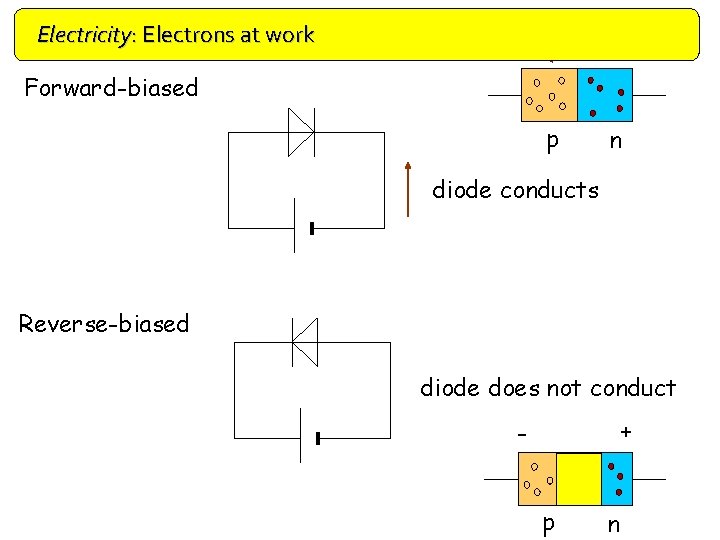
Electricity: Electrons at work Doping + - Forward-biased p n diode conducts Reverse-biased diode does not conduct + p n

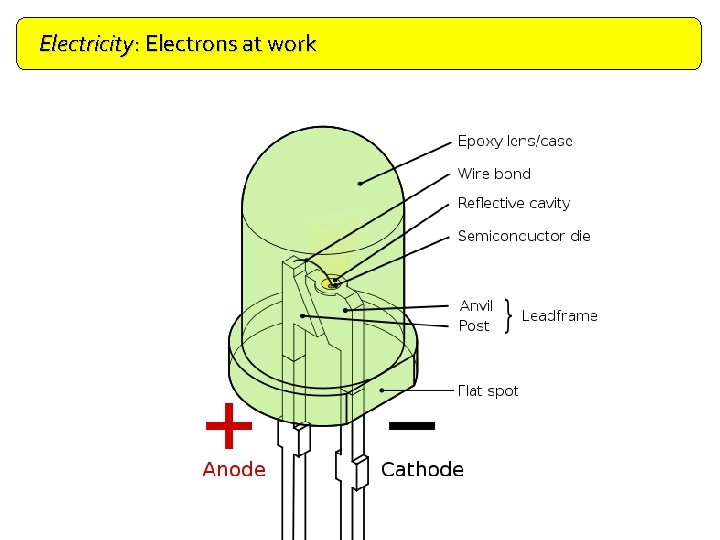
Electricity: Electrons at work Doping The Light Emitting Diode The LED has a p-n junction very close to the surface. When it is forward biased, electrons and holes cross the junction. Some of the electrons and holes meet and recombine giving out energy. The energy can be given out as a photon of light.

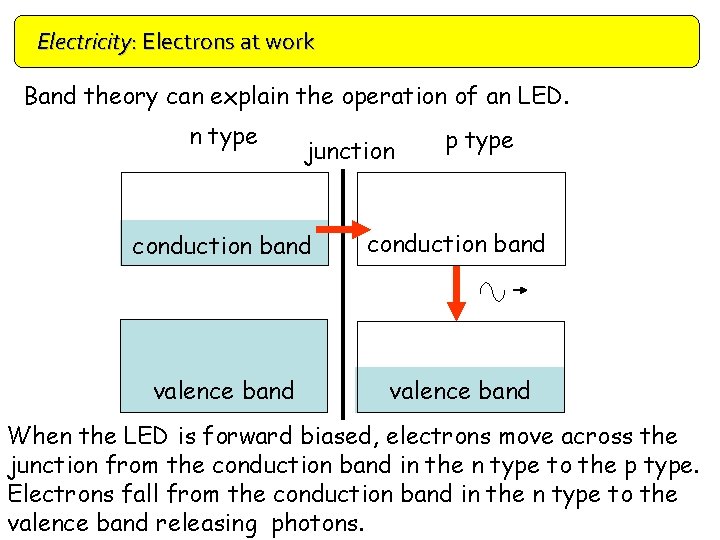
Electricity: Electrons at work Doping Band theory can explain the operation of an LED. n type junction p type conduction band valence band When the LED is forward biased, electrons move across the junction from the conduction band in the n type to the p type. Electrons fall from the conduction band in the n type to the valence band releasing photons.

Electricity: Electrons at work Doping

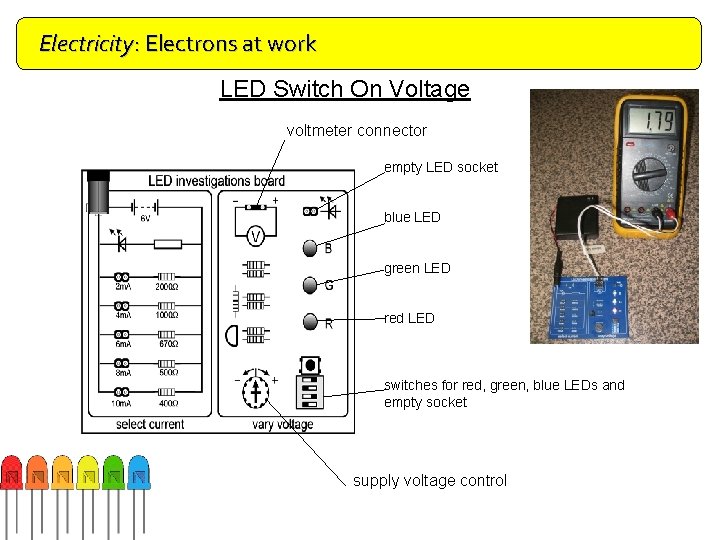
Electricity: Electrons at work Doping LED Switch On Voltage voltmeter connector empty LED socket blue LED green LED red LED switches for red, green, blue LEDs and empty socket supply voltage control

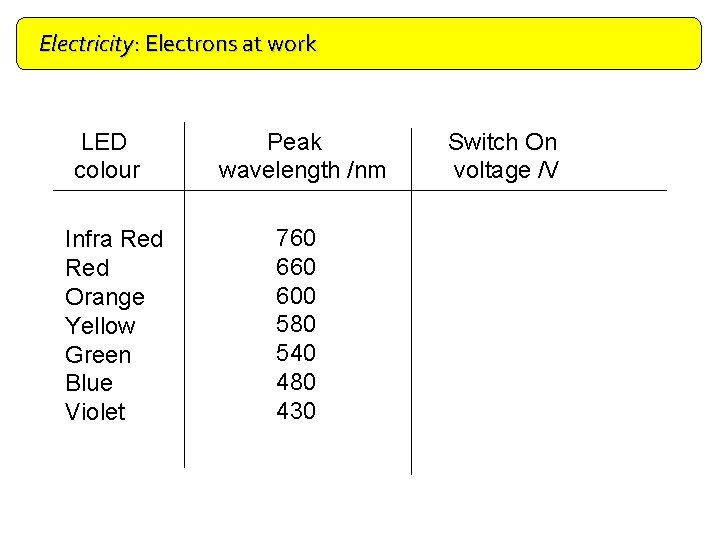
Electricity: Electrons at work Doping LED colour Infra Red Orange Yellow Green Blue Violet Peak wavelength /nm 760 600 580 540 480 430 Switch On voltage /V

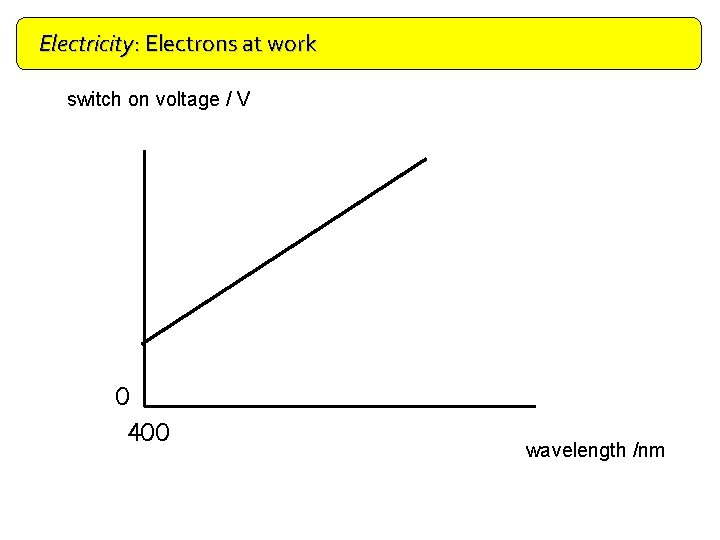
Electricity: Electrons at work Doping switch on voltage / V 0 400 wavelength /nm

Electricity: Electrons at work Doping

Electricity: Electrons at work Doping Solar Cells Photons reaching the p-n junction have their energy absorbed, freeing electrons. A voltage is created by the separation of the electrons and holes. This is called the photovoltaic effect.