Higher Order Circuits How To Obtain State Equations

Higher Order Circuits – How To Obtain State Equations? Consider a circuit with capacitor, inductors, n-terminal resistors and independent sources. Aim is to obtain state equations in the following form: state variables output variables input variables Method: - some capacitor voltages and some inductor currents (mostly all) - currents and voltages under consideration - values for independent sources Step 1: Draw the circuit graph and choose an appropriate tree: a-) Choose voltage sources as twigs, if tree is not completed continue with (b). b-) Choose capacitors as twigs (you may have to exclude some capacitors), if tree is not completed continue with (c). c-) Choose current-controlled edges of resistors as twigs, if tree is not completed continue with (d).

d-) choose inductors as twigs. Step 2: Determine the state variables: capacitor voltages in twigs and inductor currents in chords. Write element equations for state variables: Step 3: Calculate state equations: Write linearly independent current equations: KCL’s for fundamental cut-sets Write linearly independent voltage equations: KVL’s for fundamental loops Using these equations obtain currents of capacitors in twigs and voltages of inductors in chords in terms of state variables and inputs. Which elements are these?

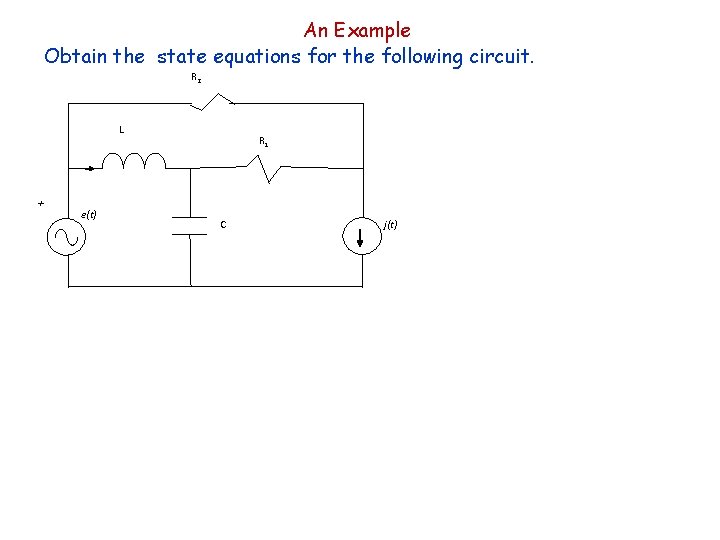
An Example Obtain the state equations for the following circuit. R 2 L + e(t) R 1 C j(t)

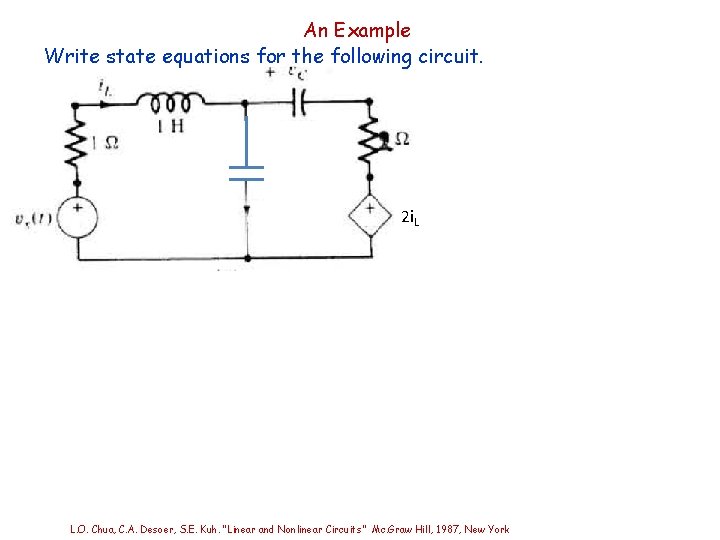
An Example Write state equations for the following circuit. 2 i. L L. O. Chua, C. A. Desoer, S. E. Kuh. “Linear and Nonlinear Circuits” Mc. Graw Hill, 1987, New York

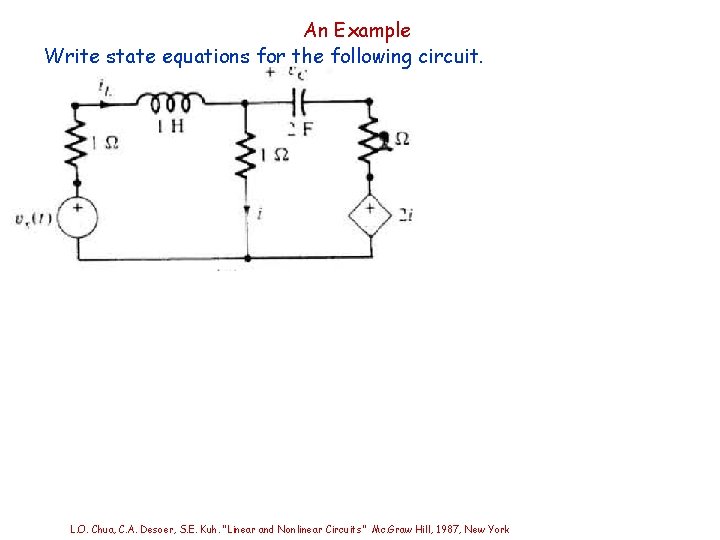
An Example Write state equations for the following circuit. L. O. Chua, C. A. Desoer, S. E. Kuh. “Linear and Nonlinear Circuits” Mc. Graw Hill, 1987, New York

Solutions of 2. Order Differential Equations Solution can be obtained as the sum of the solution of the homogeneous equation and the particular solution: Homogeneous equation: exponential solution as a guess What should we find now? S=0 is of course a solution, but can we find a nonzero solution too? Characteristic Equation

Roots of the characteristic polynomial: Also need to find : eigenvectors eigenvalues An element of Solve this to find the eigenvector for Particular Solution: (should be found by quess method) Total solution:

State Transition Matrix zero-input solution zero-state solution

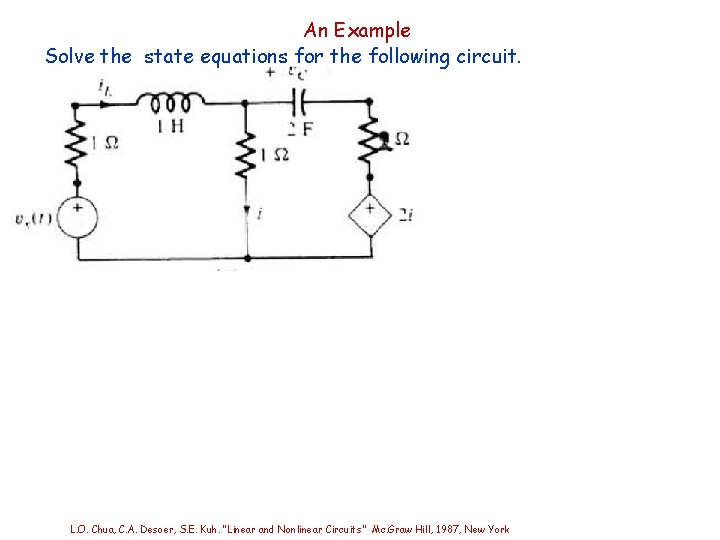
An Example Solve the state equations for the following circuit. L. O. Chua, C. A. Desoer, S. E. Kuh. “Linear and Nonlinear Circuits” Mc. Graw Hill, 1987, New York

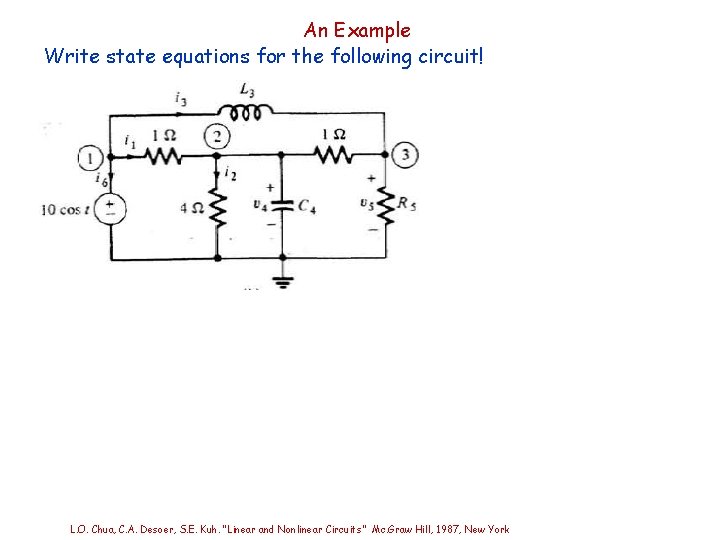
An Example Write state equations for the following circuit! L. O. Chua, C. A. Desoer, S. E. Kuh. “Linear and Nonlinear Circuits” Mc. Graw Hill, 1987, New York

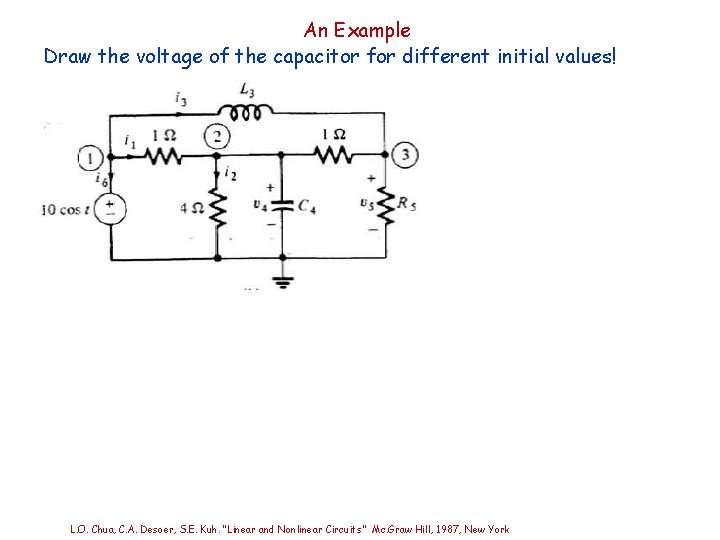
An Example Draw the voltage of the capacitor for different initial values! L. O. Chua, C. A. Desoer, S. E. Kuh. “Linear and Nonlinear Circuits” Mc. Graw Hill, 1987, New York

A constant solution of a dynamical system: Equilibrium How many equilibria are there? What happens near the equlibrium? Definition: Lyapunov stability Let be an equilibrium of the system given by The equilibrium is Lyapunov stable if for every such that A Lyapunov stable equilibrium exists a such that . there exists a is asymptotically stable if there.

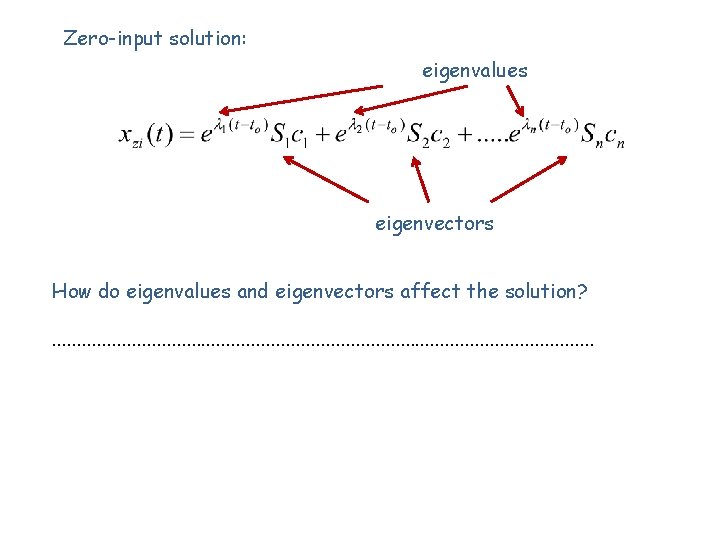
Zero-input solution: eigenvalues eigenvectors How do eigenvalues and eigenvectors affect the solution? . . . . . . .

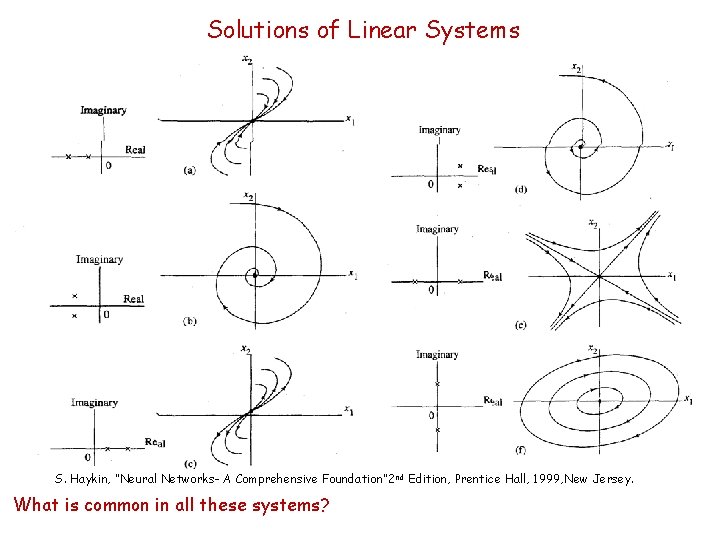
Solutions of Linear Systems S. Haykin, “Neural Networks- A Comprehensive Foundation” 2 nd Edition, Prentice Hall, 1999, New Jersey. What is common in all these systems?