Highaccuracy calculations in H 2 JeanPhilippe Karr Laurent

High-accuracy calculations in H 2+ Jean-Philippe Karr, Laurent Hilico Laboratoire Kastler Brossel (UPMC/ENS) Université d’Evry Val d’Essonne Vladimir Korobov Joint Institute for Nuclear Research Dubna, Russia

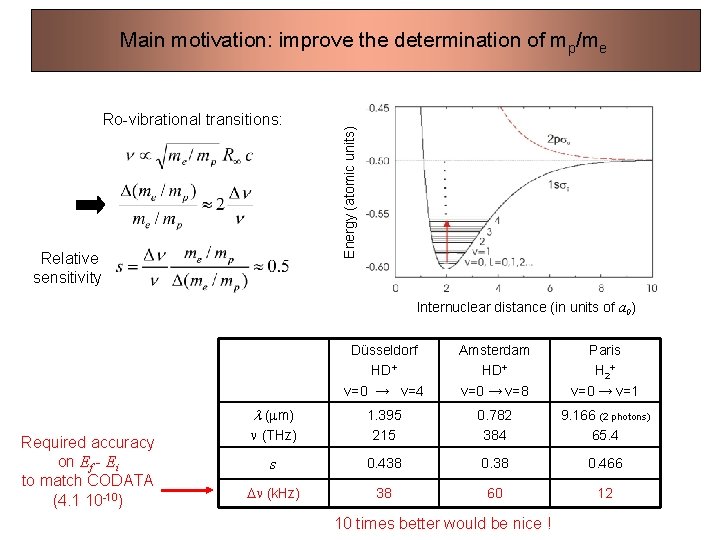
Ro-vibrational transitions: Relative sensitivity Energy (atomic units) Main motivation: improve the determination of mp/me Internuclear distance (in units of a 0) Düsseldorf HD+ v=0 → v=4 Amsterdam HD+ v=0 → v=8 Paris H 2+ v=0 → v=1 n (THz) 1. 395 215 0. 782 384 9. 166 (2 photons) 65. 4 s 0. 438 0. 466 Dn (k. Hz) 38 60 12 l (mm) Required accuracy on Ef - Ei to match CODATA (4. 1 10 -10) 10 times better would be nice !

Theory : present status H 2 + Two-photon transition frequency (v=0, L=2, J=5/2) (v=1, L=2, J=5/2) DEnr DE (a 4) DE (a 5) QED corrections DE (a 6) nonrecoil DE (a 7) with recoil Proton structure DEp (leading) Hyperfine sructure DE (5/2→ 5/2) Total DEtot n 2 ph 65 412 414. 3359 } 1 077. 303(03) -274. 146(02) -1. 980 0. 119(23) V. I. Korobov PRA 77, 022509 (2008) and ref. therein in progress -0. 041(0. 3) V. I. Korobov, L. Hilico, J. -Ph. Karr -2. 591(02) PRA 74, 040502(R) (2006) PRA 79, 012501 (2009) 65 413 213. 001(24) 32 706 606. 500(12) MHz 8 10 -10 Improvement by 2 orders of magnitude

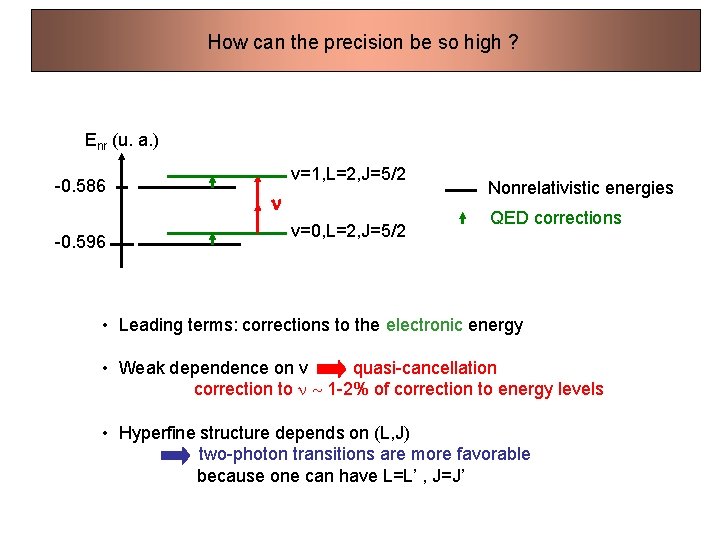
How can the precision be so high ? Enr (u. a. ) -0. 586 -0. 596 v=1, L=2, J=5/2 n v=0, L=2, J=5/2 Nonrelativistic energies QED corrections • Leading terms: corrections to the electronic energy • Weak dependence on v quasi-cancellation correction to n 1 -2% of correction to energy levels • Hyperfine structure depends on (L, J) two-photon transitions are more favorable because one can have L=L’ , J=J’

Theoretical approach • At high orders (ma 6 and above) it is sufficient to consider the correction to the electron in the field of the nuclei (nonrecoil limit) e r 1 r 2 Similar to H atom with instead of • Effective Hamiltonian approach: p R p QED corrections are expressed as effective operator mean values • For a grid of values of R, we obtain very precise 1 ssg electronic wave functions (DE 10 -20 a. u. ) Variational expansion: Exponents ai, bi are chosen in a quasi-random way. Ts. Tsogbayar and V. I. Korobov J. Chem. Phys. 125, 024308 (2006) Energy corrections are obtained in a form DEQED(R) Average over ro-vibrational wave functions to get DEQED(v, L)

The one-loop electron self-energy at order (ma)7 Ø A long-standing problem in hydrogen atom calculations - First high-precision calculation of A 60 for 1 S and 2 S states K. Pachucki, Ann. Phys. 226, 1 (1993) - Derivation of effective operators following NRQED approach; 1 S-n. S difference U. D. Jentschura, A. Czarnecki, K. Pachucki, PRA 72, 062102 (2005) Ø These methods must be adapted to the H 2+ case the wave functions are not known analytically numerical calculations NB. The required precision is not too high ( 10 -3)

General one-loop result System: electron in an external potential V Valid for l ≠ 0 states and S-state difference: the high-energy part in d(r) drops out Rel. Bethe log. U. D. Jentschura, A. Czarnecki, K. Pachucki, PRA 72, 062102 (2005)

Low energy part: relativistic Bethe logarithm Ø Leading order a(Za)4 Bethe logarithm • Term in ln(l) cancelled by the high energy part • Term in l cancelled by mass counter-term Ø Order a(Za)6 : relativistic corrections to the Bethe logarithm HR HR _ HR Relativistic dipole Nonrelativistic quadrupole Relativistic correction to the current

Numerical approach Ø Calculate numerically the integrands using a variational wave function Ø Numerical integration: Ø Find the asymptotic behavior of P(k) at k → ∞ - first order perturbation wave function y 1 : - approximate form of y 1 for k → : Example: Following terms are evaluated by a fitting procedure. Ø Analytical integration of the asymptotic form for k > L

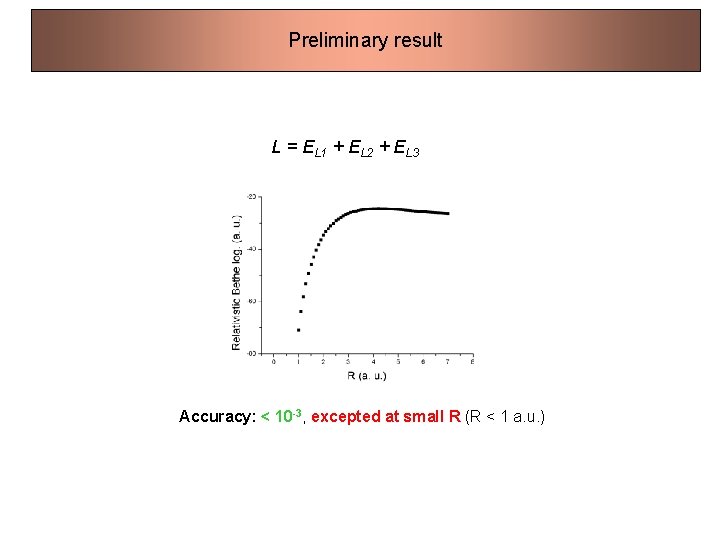
Preliminary result L = EL 1 + EL 2 + EL 3 Accuracy: < 10 -3, excepted at small R (R < 1 a. u. )

Other contributions Ø Some of these operator mean values are divergent for S states (in H) or for the 1 Ssg electronic state (in H 2+) Ø Analytical work to extract the divergent part Ø The obtained finite expression differs from the exact H(1 S) result of K. Pachucki, Ann. Phys. 226, 1 (1993) by the high-energy part i. e. some constant C times (or in H 2+). The coefficient C is easily deduced from comparison between the expressions.

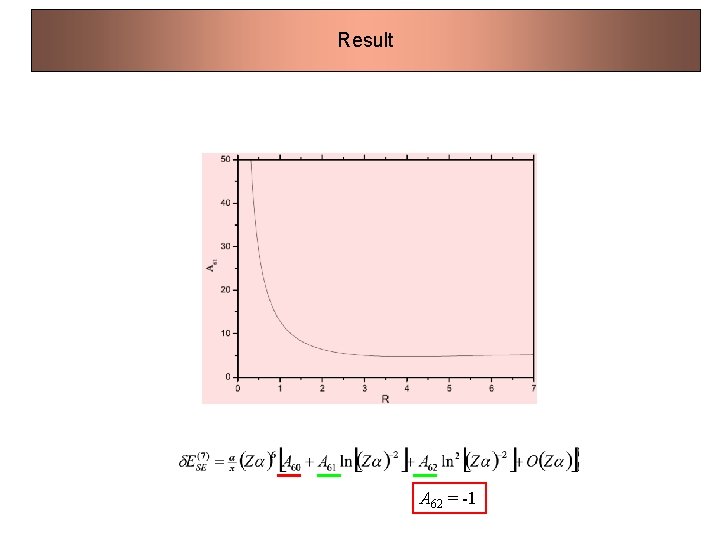
Result A 62 = -1

Conclusion Last steps: Ø Refine the numerical method for low-energy part accurate values of A 60(R) for all R. Ø Average over ro-vibrational wave functions correction to ro-vibrational levels. Theoretical accuracy ~ 1 k. Hz on n OK for significantly improved determination of mp/me What’s next ? ØTwo-loop self-energy at order ma 2(Za)6 Ø Vacuum polarization terms Ø …

And now, for something completely different The muonic hydrogen experiment revisited by U. Jentschura: Ann. Phys. 326, 500 -515 and 516 -533 (2011). The observed discrepancy : nexp = ntheor + 0. 31 me. V might be due to the pm atom forming a 3 -body quasibound state (resonance) with an electron in the H 2 gas target. ? Order-of magnitude estimate: “In order to assess the validity of the pm-e- atom hypothesis, one would have to calculate its spectrum, its ionization cross sections in collisions with other molecules in the gas target. Furthermore, it would be necessary to study the inner Auger rates of pm-e- as a function of the state of the outer electron, and its production cross sections in the collisions that take place in the molecular hydrogen target used in the experiment. ” pm (2 S) e-

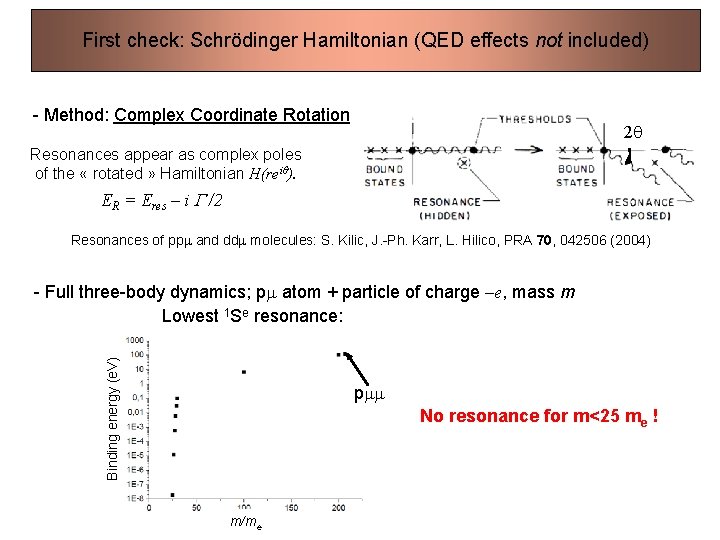
First check: Schrödinger Hamiltonian (QED effects not included) - Method: Complex Coordinate Rotation 2 q Resonances appear as complex poles of the « rotated » Hamiltonian H(reiq). ER = Eres – i G /2 Resonances of ppm and ddm molecules: S. Kilic, J. -Ph. Karr, L. Hilico, PRA 70, 042506 (2004) Binding energy (e. V) - Full three-body dynamics; pm atom + particle of charge –e, mass m Lowest 1 Se resonance: pmm No resonance for m<25 me ! m/me

…but QED shifts must be included Long-range atom-electron interaction potential: A: dipole moment a: dipole polarizability Charge-dipole Charge-induced dipole Schrödinger Hamiltonian: A ≠ 0 (2 S-2 P degeneracy) With QED shifts: A = 0 V(R) ~ 1/R 2 V(R) ~ 1/R 4 How to add QED level shifts to the Schrödinger Hamiltonian ? Ø 1 Po resonances of H- below n=2: E. Lindroth, PRA 57, R 685 (1998) discrete numerical basis set, obtained by discretization of the one-particle Hamiltonian on a radial mesh. Ø Add the Uehling potential 2 S-2 P Lambshift (without FS and HFS): 207. 6358 me. V One-loop vacuum polarization: 205. 1584 me. V

The Uëhling potential where r = a mr r x = me/a mr ≈ 0. 737… Vvp(r) ~ ln(r)/r at r → 0 Exponential decrease at r → E. A. Uehling, Phys. Rev. 48, 55 (1935) ü Matrix elements of the Uehling potential can be obtained analytically See also: A. M. Frolov and D. M. Wardlaw, for exponential basis functions ar. Xiv: 1110. 3433 v 1 (15/10/2011) ü Nonperturbative treatment: Schrödinger equation with Coulomb + Uehling potential ü Check: Consistent with published results for muonic systems Energy shift (me. V) pm 2 S-2 P -205. 1584 ppm ground state -285 ddm ground state -413 U. D. Jentschura, Ann. Phys. 326, 500 -515 (2011). } G. A. Aissing and H. J. Monkhorst, PRA. 42, 7389 (1990) (1 st order pert. ).

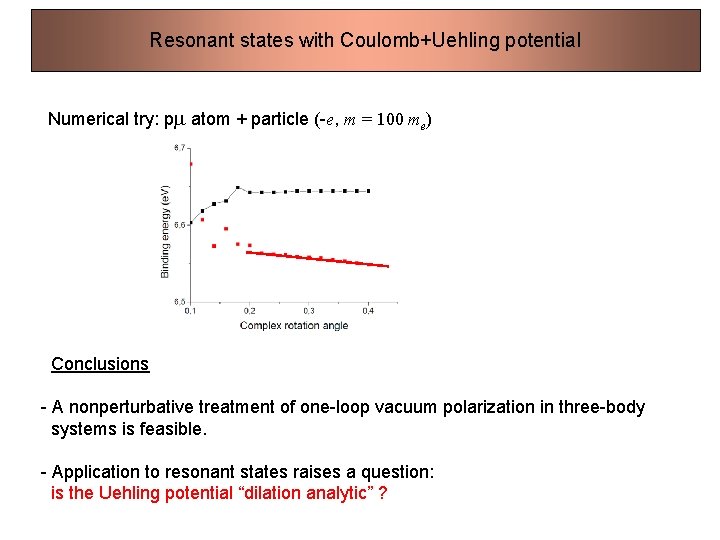
Resonant states with Coulomb+Uehling potential Numerical try: pm atom + particle (-e, m = 100 me) Conclusions - A nonperturbative treatment of one-loop vacuum polarization in three-body systems is feasible. - Application to resonant states raises a question: is the Uehling potential “dilation analytic” ?