High Sensitivity Magnetic Gradiometer for Earthquake Research Applications

High Sensitivity Magnetic Gradiometer for Earthquake Research Applications ISRAEL 2005 Ivan Hrvoic H. Ginzburg, H. Zafrir, G. Steinitz, B. Shirman, G. Hollyer

Overview • Magnetic Earthquake Research Methods – Introduction to Past and Current Methods – Detectability of Earthquakes by Gradiometers – Short Base (Gradient) Measurements • Potassium Super. Gradiometer – Installation and Data Records • Summary

Introduction to Magnetics • Several decades of investigation • Based on theory of piezomagnetism and / or electrokinetics • Possibility of detection is related to gradual pressure build-up prior to earthquakes or “events”

Monitoring Systems (1) • Traditional Methods – Magnetic sensors (0. 1 n. T sensitivity) – Long base measurements • Some startling results • No duplication of results • Recent Work – Induction coils • Improved sensitivity to 25 p. T • But, limited bandwidth (0. 01 Hz)

Monitoring Systems (2) • Induction Coils – Detect first derivative of magnetic field – Detect all 3 components – Skin Effect Problems • 50 km @ 0. 01 Hz • 1. 6 km @ 10 Hz

Detectability of Earthquakes by Gradiometers • Assuming earthquakes create dipolar anomalies, can calculate detectability of earthquakes of given magnitude: • Where o is magnetic permeability, M is magnetic moment, and α is the angle between radius vector, r, and dipole direction. • r is distance from hypocenter to the observation point

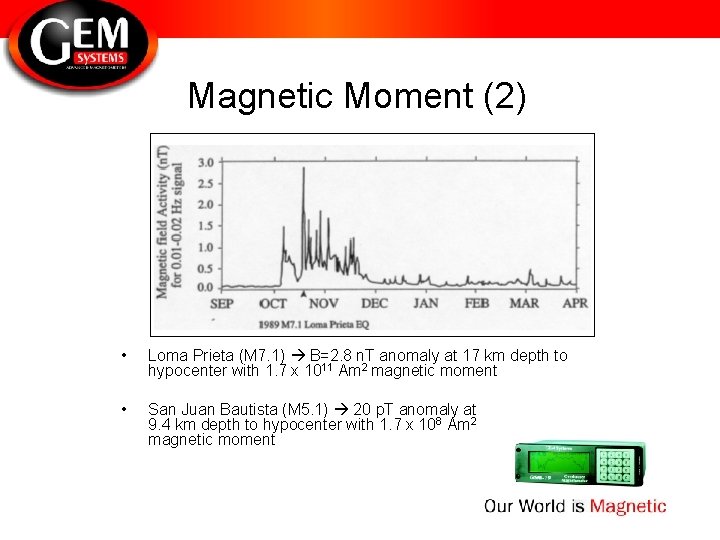
Magnetic Moment (1) • Assuming cos 2 = 0 for simplicity, the previous equation can be solved for M, Magnetic Moment, as follows: • Results are extended to look at data from the Loma Prieta earthquake of 1989 which clearly shows magnetic precursors.

Magnetic Moment (2) • Loma Prieta (M 7. 1) B=2. 8 n. T anomaly at 17 km depth to hypocenter with 1. 7 x 1011 Am 2 magnetic moment • San Juan Bautista (M 5. 1) 20 p. T anomaly at 9. 4 km depth to hypocenter with 1. 7 x 108 Am 2 magnetic moment

Radius Calculation (1) • Note the 3 rd potential drop off of the magnetic field and the 4 th potential of the magnetic gradient with radius: • Extreme sensitivity needed to measure (d. B / dr) • Prospects for elimination of man-made noise are better

Radius Calculation (2) • Maximum distance at which an event can be detected by different sensors • Skin effect not taken into account

Potassium Super. Gradiometer

Super. Grad Array • 3 sensors arranged according to terrain (horizontal or vertical) S 2 140 m 100 m S 3 100 m Computer • Sensor spacing up to 140 m • Long term integration is promising S 1

Data (1)

Data (2)

Data (3)

Installations • Currently in use near Dead Sea, Israel • Measures fields at 3 sensors, 20 times per second with 50 msec and 1 sec integration • 6 channels of data to 1 f. T resolution • GPS receiver provides Universal Time • Noise background is about 0. 1 p. T for 1 sec integration; giving 2 f. T/m sensitivity at 50 m spacing • Since July 2002, has acquired more than 10 billion readings; likely the most ever recorded for this type of application

Initial Installation - Israel

Data - Israel p. T 8 hours

Additional Installations • System deployed in Magnetic observatory of the Geological Survey of Canada near Ottawa • Test of basic system configuration for 6 months – Remote operation – Downloading of data via internet or telephone • Installation in Mexico (Oaxaca State) – Photos and records from Mexico • Also seeking other jurisdictions for siting system; potentially in regions of more active tectonism

Site Location- Mexico

Site Selection - Mexico

Site Survey Data - Mexico

Gradient Survey Data - Mexico

Sensor Installation - Mexico

Data Acquisition & Communication - Mexico

Data - Mexico p. T sec

Integrated Grad / Radon • Complementary radon emanation measurements. • Correlation with weak earthquakes in Dead Sea rift region • The combined Supergradiometer / Radon system is now available for application by various groups pursuing earthquake research studies.

Summary • Based on earlier assumptions (and not considering geometrical effects), we can conclude: – Magnetometers of 1 n. T sensitivity can detect only the strongest earthquakes (M >7) – Induction coils are good for M>6 – Super. Gradiometer in Fast mode is effective for M>6 – Super. Gradiometer in Slow mode is effective for M>5