High Resolution Microwave Spectroscopy of CH Molecule Search

High Resolution Microwave Spectroscopy of CH Molecule Search for Variation of Fundamental Constants Stefan Truppe

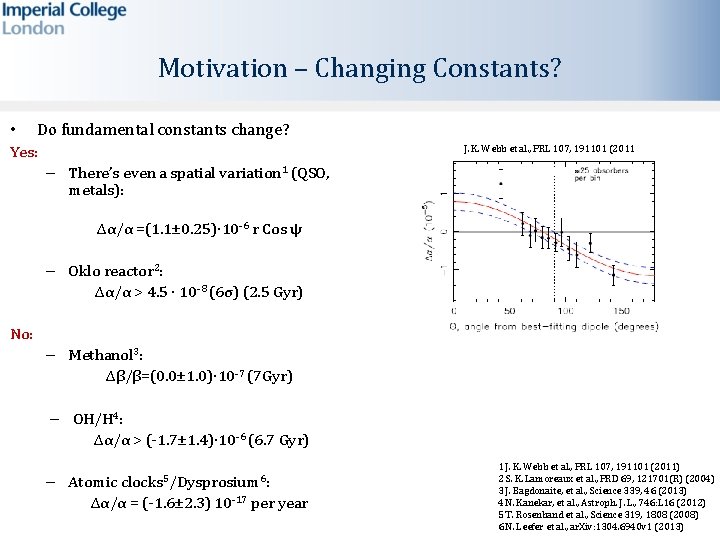
Motivation – Changing Constants? • Do fundamental constants change? Yes: J. K. Webb et al. , PRL 107, 191101 (2011 – There’s even a spatial variation 1 (QSO, metals): Δα/α =(1. 1± 0. 25)⋅10 -6 r Cos ψ – Oklo reactor 2: Δα/α > 4. 5 ⋅ 10 -8 (6σ) (2. 5 Gyr) No: – Methanol 3: Δβ/β=(0. 0± 1. 0)⋅10 -7 (7 Gyr) – OH/H 4: Δα/α > (-1. 7± 1. 4)⋅10 -6 (6. 7 Gyr) clocks 5/Dysprosium 6: – Atomic Δα/α = (-1. 6± 2. 3) 10 -17 per year 1 J. K. Webb et al. , PRL 107, 191101 (2011) 2 S. K. Lamoreaux et al. , PRD 69, 121701(R) (2004) 3 J. Bagdonaite, et al. , Science 339, 46 (2013) 4 N. Kanekar, et al. , Astroph. J. L. , 746: L 16 (2012) 5 T. Rosenband et al. , Science 319, 1808 (2008) 6 N. Leefer et al. , ar. Xiv: 1304. 6940 v 1 (2013)

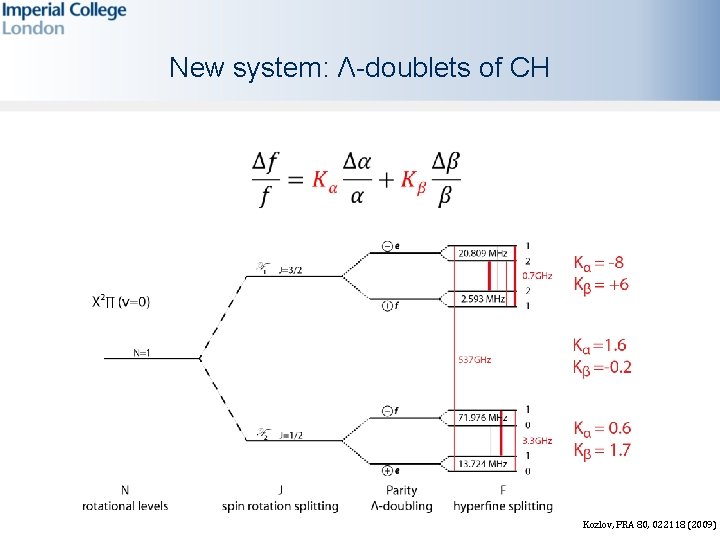
New system: Λ-doublets of CH

New system: Λ-doublets of CH Kozlov, PRA 80, 022118 (2009)

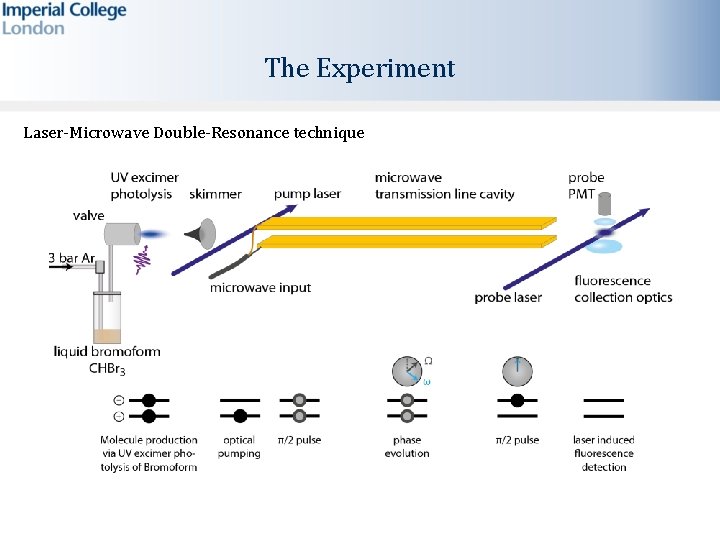
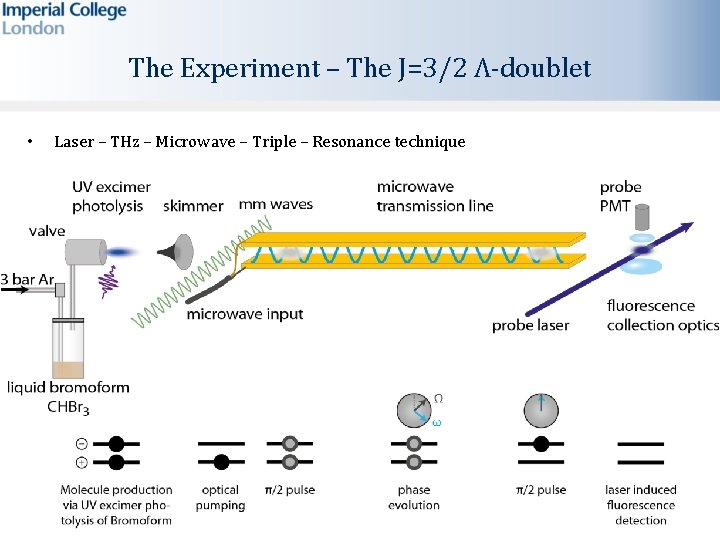
The Experiment Laser-Microwave Double-Resonance technique

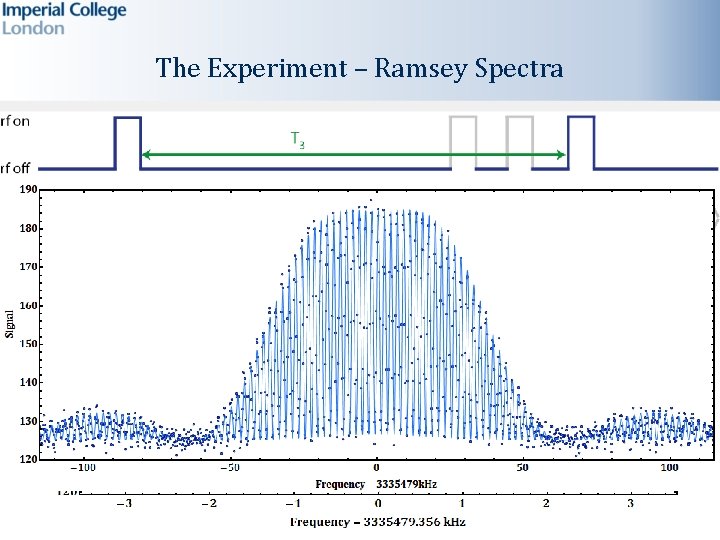
The Experiment – Ramsey Spectra

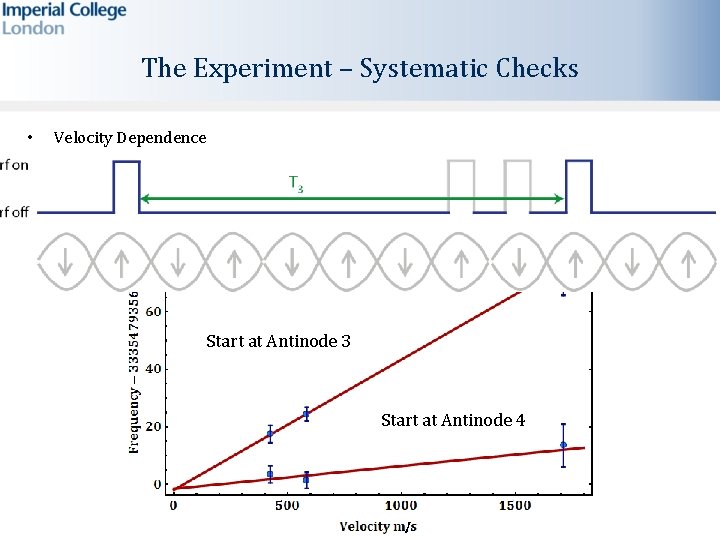
The Experiment – Systematic Checks • Velocity Dependence He Start at Antinode 3 Ar Kr Start at Antinode 4

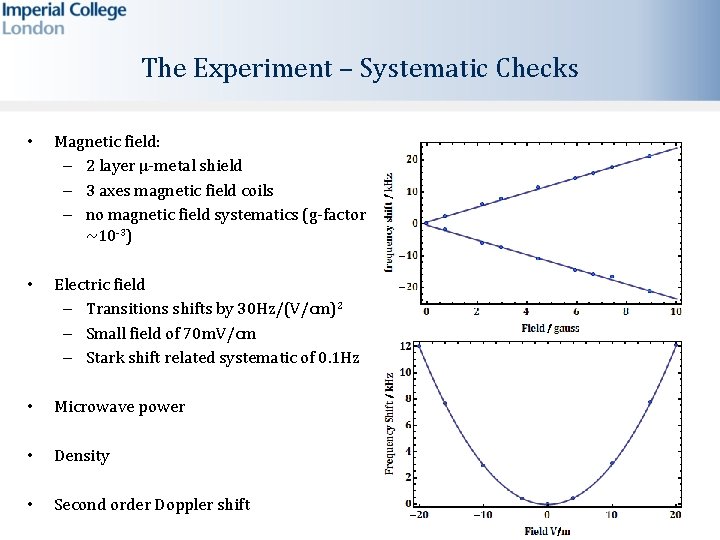
The Experiment – Systematic Checks • Magnetic field: – 2 layer μ-metal shield – 3 axes magnetic field coils – no magnetic field systematics (g-factor ~10 -3) • Electric field – Transitions shifts by 30 Hz/(V/cm)2 – Small field of 70 m. V/cm – Stark shift related systematic of 0. 1 Hz • Microwave power • Density • Second order Doppler shift

The Experiment – J=1/2 Results Transition Resonance Frequency [Hz] (1/2+, 1) – (1/2 -, 1) (1/2+, 0) – (1/2 -, 1) (1/2+, 1) – (1/2 -, 0) (3/2+, 2) – o r to (3/2 -, 2) (3/2+, 1) – (3/2 -, 1) e v o (3/2+, 1) – (3/2 -, 2) pr Im y b d (3/2+, 2) – (3/2 -, 1) c a f a 0 0 3 f

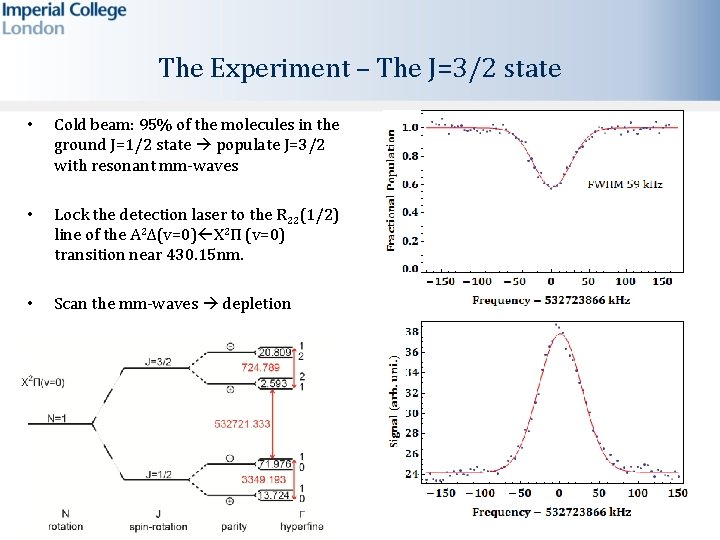
The Experiment – The J=3/2 state • Cold beam: 95% of the molecules in the ground J=1/2 state populate J=3/2 with resonant mm-waves • Lock the detection laser to the R 22(1/2) line of the A 2Δ(v=0) X 2Π (v=0) transition near 430. 15 nm. • Scan the mm-waves depletion

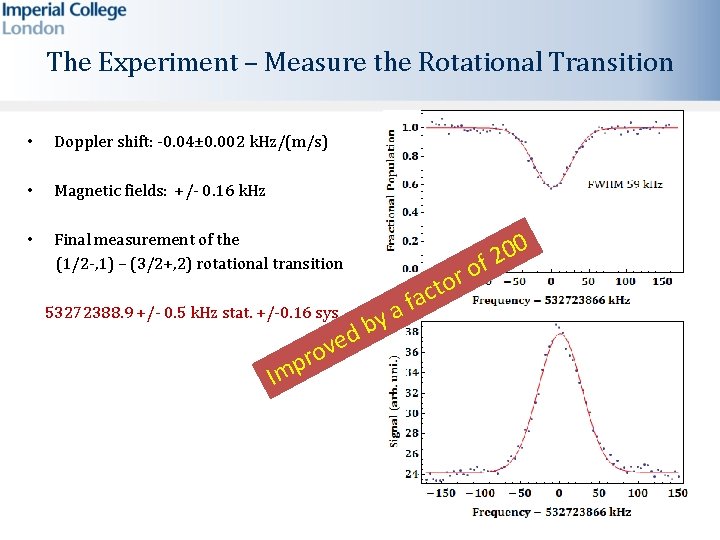
The Experiment – Measure the Rotational Transition • Doppler shift: -0. 04± 0. 002 k. Hz/(m/s) • Magnetic fields: +/- 0. 16 k. Hz • Final measurement of the (1/2 -, 1) – (3/2+, 2) rotational transition 53272388. 9 +/- 0. 5 k. Hz stat. +/-0. 16 sys ro p Im b d ve fa a y r o t c o 0 0 2 f

The Experiment – The J=3/2 Λ-doublet • Laser – THz – Microwave – Triple – Resonance technique • Statistical uncertainty(1 -σ) 5 Hz after 20 min of averaging • Systematic shift with magnetic field!

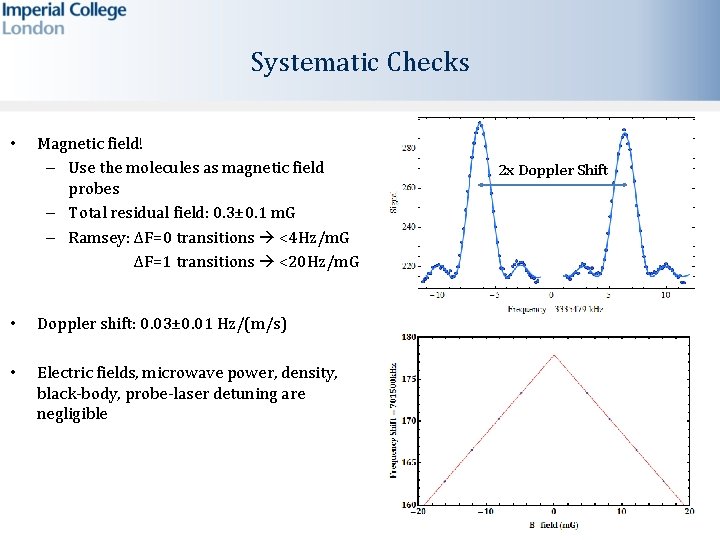
Systematic Checks • Magnetic field! – Use the molecules as magnetic field probes – Total residual field: 0. 3± 0. 1 m. G – Ramsey: ΔF=0 transitions <4 Hz/m. G ΔF=1 transitions <20 Hz/m. G • Doppler shift: 0. 03± 0. 01 Hz/(m/s) • Electric fields, microwave power, density, black-body, probe-laser detuning are negligible 2 x Doppler Shift

Summary 2 Transition Resonance Frequency [Hz] (1/2+, 1) – (1/2 -, 1) t e l ub (1/2+, 0) – (1/2 -, 1) (1/2+, 1) – (1/2 -, 0) (3/2+, 2) – (3/2 -, 2) s t n e 2 / 3 = J e o d Λ th f o (3/2+, 1) – (3/2 -, 1) m e r u as -, 2) (3/2+, 1) – (3/2 e m b la+, 2) – (3/2 -, 1) t (3/2 s Fir (1/2 -, 1) – (3/2+, 2) 532723889000 +/- 600

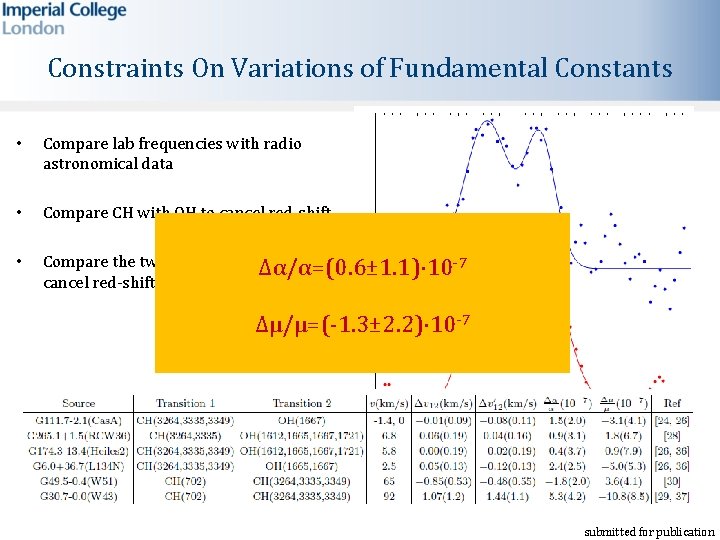
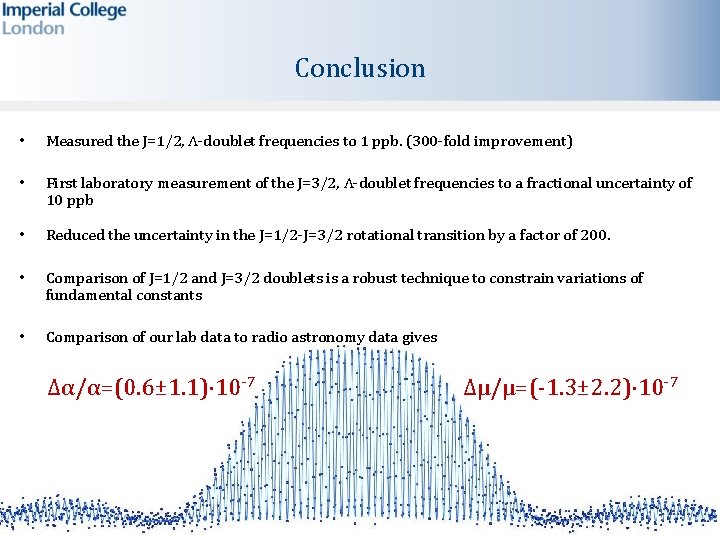
Constraints On Variations of Fundamental Constants • Compare lab frequencies with radio astronomical data • Compare CH with OH to cancel red-shift • Compare the two Λ-doublets of CH to -7 Δα/α=(0. 6± 1. 1)⋅10 cancel red-shift Δμ/μ=(-1. 3± 2. 2)⋅10 -7 submitted for publication

Outlook • Dedicated astronomical measurements even higher precision and sources at high redshift • Telescopes: – 100 m dish at Effelsberg (MPG) – 100 m Green Bank Telescope (NRAO) – VLA (NRAO) – 300 m Telescope at Arecibo – New 500 m Telescope in Guizhou China – Square Kilometer Array in South Africa and Australia – Measurement of the rotational transitions using ALMA Δα/α or Δμ/μ ~ 10 -8 is possible

Conclusion • Measured the J=1/2, Λ-doublet frequencies to 1 ppb. (300 -fold improvement) • First laboratory measurement of the J=3/2, Λ-doublet frequencies to a fractional uncertainty of 10 ppb • Reduced the uncertainty in the J=1/2 -J=3/2 rotational transition by a factor of 200. • Comparison of J=1/2 and J=3/2 doublets is a robust technique to constrain variations of fundamental constants • Comparison of our lab data to radio astronomy data gives Δα/α=(0. 6± 1. 1)⋅10 -7 Δμ/μ=(-1. 3± 2. 2)⋅10 -7

Thanks Mike Tarbutt Misha Kozlov Rich Hendricks & Sean Tokunaga Heather Lewandowski Ed Hinds