HIGH PERFORMANCE COMPUTING Parallelism and Performance Metrics Master

HIGH PERFORMANCE COMPUTING Parallelism and Performance Metrics Master Degree Program in Computer Science and Networking Academic Year 2020 -2021 Dr. Gabriele Mencagli, Ph. D Department of Computer Science University of Pisa, Italy 27/02/2021 High Performance Computing, G. Mencagli 1

Contents § We introduce a small example to present the course methodology and approach • We start from the sequential definition of a system • We study how to detect bottlenecks • We study how to remove bottlenecks by introducing feasible parallelizations § Definition of performance metrics • • • § § § Ideal service time and caching impact Parallelism degree Completion time Inter-process communication latency Bandwidth and relative efficiency Strong and weak scalability concepts Communication overlapping Utilization of prerequisites Parts of the book covered by these slides • Sections 1. 4. 1, 2, 3. 3, 4. 1. 1, 4. 2. 1, 4. 4 and 4. 5 • Appendices of the book (Parts 4, 7 and 8) 27/02/2021 High Performance Computing, G. Mencagli 2

Introductory Statement These slides contain a reminder on prerequisites It must be used to test your background knowledge (Book Appendix) 27/02/2021 High Performance Computing, G. Mencagli 3

Running Example 27/02/2021 High Performance Computing, G. Mencagli 4

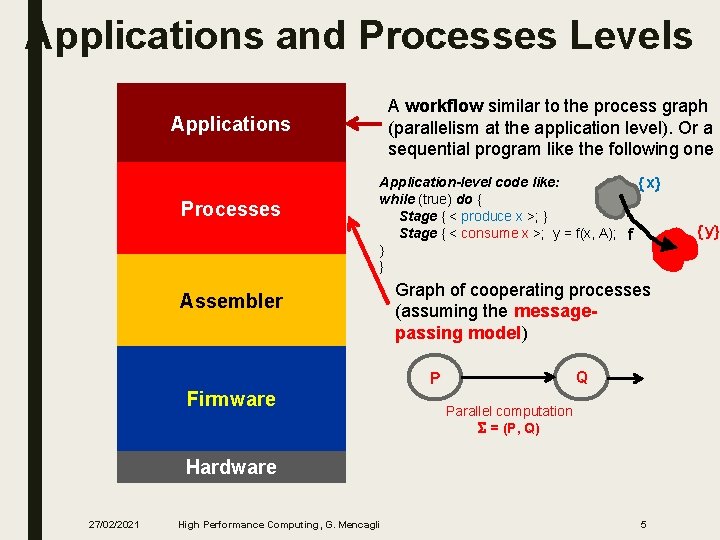
Applications and Processes Levels A workflow similar to the process graph (parallelism at the application level). Or a sequential program like the following one Applications Processes Application-level code like: x while (true) do { Stage { < produce x >; } Stage { < consume x >; y = f(x, A); f } Assembler Graph of cooperating processes (assuming the messagepassing model) Q P Firmware Parallel computation S = (P, Q) Hardware 27/02/2021 High Performance Computing, G. Mencagli 5 y

Problem Statement A simple graph of two processes operating on data streams (simple producer-consumer pattern) x P illimited-length stream of integers (x) x send x onto input_stream Note: x is not shared, P and Q have their own private variable x. N will be fixed during the analysis 27/02/2021 output_stream Parallel computation S = (P, Q) A[N] P: : int x; ouput input_stream; … while (true) do x = <generate new value> y Q input_stream generates the stream elements (x is the generic stream element) illimited-length stream of integers (y) transforms the stream elements y = f(x, A) encapsulates a statically initialized integer array A[N] Q: : int x, y; int A[N]; input_stream (…), output_stream; while (true) do receive x from input_stream; y = 0; for i = 0 to N – 1 if (x = A[i]) then y = y +1; send y onto output_stream High Performance Computing, G. Mencagli 6

Analysis of Process Q § § § Assumption: we initially neglect the impact of communications Analysis of process Q’s service time Utilization of background concepts and techniques • • • § First definition of performance metrics • • • § Addressing spaces Assembler code CPU firmware interpretation Cache architecture, management and evaluation … Service time, processing bandwidth (throughput) Utilization factor Optimal parallelism degree Latency Completion time … Introduction of the concepts of bottleneck and parallelization 27/02/2021 High Performance Computing, G. Mencagli 7

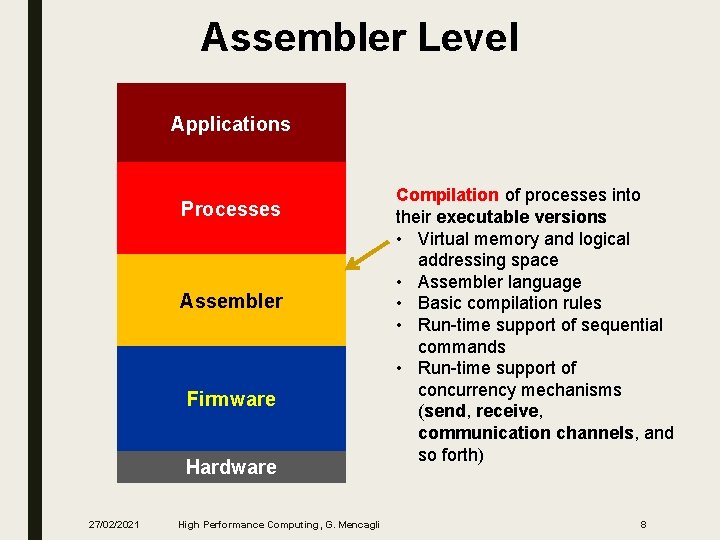
Assembler Level Applications Processes Assembler Firmware Hardware 27/02/2021 High Performance Computing, G. Mencagli Compilation of processes into their executable versions • Virtual memory and logical addressing space • Assembler language • Basic compilation rules • Run-time support of sequential commands • Run-time support of concurrency mechanisms (send, receive, communication channels, and so forth) 8

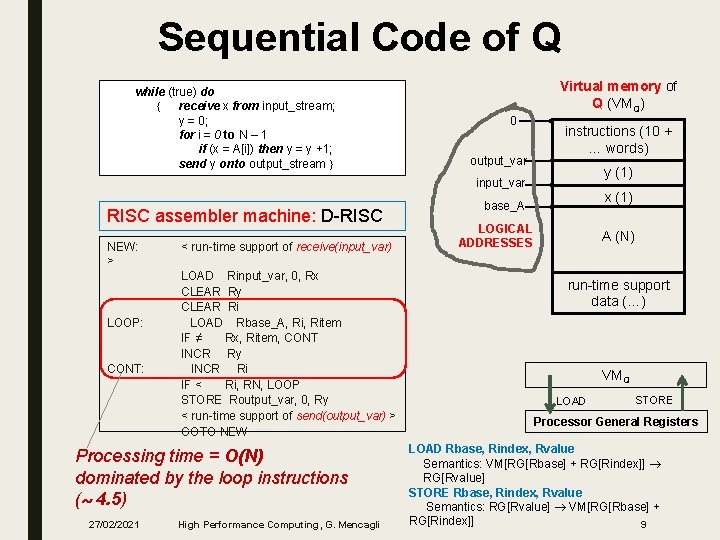
Sequential Code of Q while (true) do receive x from input_stream; y = 0; for i = 0 to N – 1 if (x = A[i]) then y = y +1; send y onto output_stream Virtual memory of Q (VMQ) 0 output_var instructions (10 + … words) y (1) input_var RISC assembler machine: D-RISC NEW: > < run-time support of receive(input_var) LOAD Rinput_var, 0, Rx CLEAR Ry CLEAR Ri LOOP: LOAD Rbase_A, Ritem IF ≠ Rx, Ritem, CONT INCR Ry CONT: INCR Ri IF < Ri, RN, LOOP STORE Routput_var, 0, Ry < run-time support of send(output_var) > GOTO NEW Processing time = O(N) dominated by the loop instructions ( 4. 5) 27/02/2021 High Performance Computing, G. Mencagli x (1) base_A LOGICAL ADDRESSES A (N) run-time support data (…) VMQ LOAD STORE Processor General Registers LOAD Rbase, Rindex, Rvalue Semantics: VM[RG[Rbase] + RG[Rindex]] RG[Rvalue] STORE Rbase, Rindex, Rvalue Semantics: RG[Rvalue] VM[RG[Rbase] + RG[Rindex]] 9

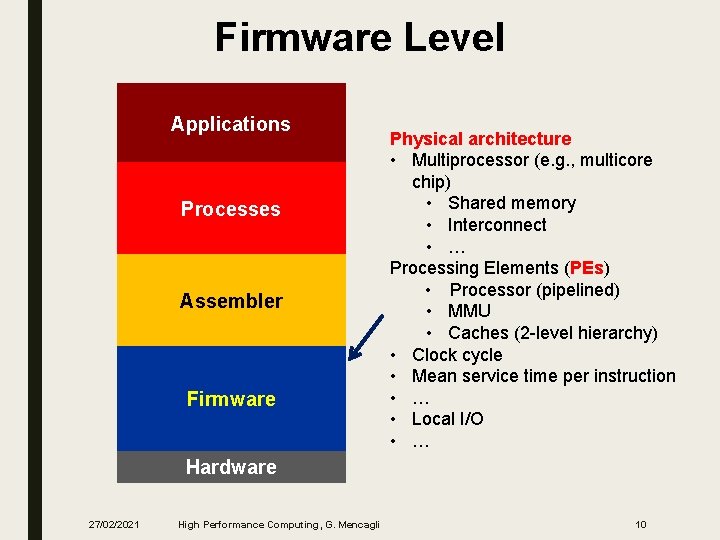
Firmware Level Applications Processes Assembler Firmware Physical architecture • Multiprocessor (e. g. , multicore chip) • Shared memory • Interconnect • … Processing Elements (PEs) • Processor (pipelined) • MMU • Caches (2 -level hierarchy) • Clock cycle • Mean service time per instruction • … • Local I/O • … Hardware 27/02/2021 High Performance Computing, G. Mencagli 10

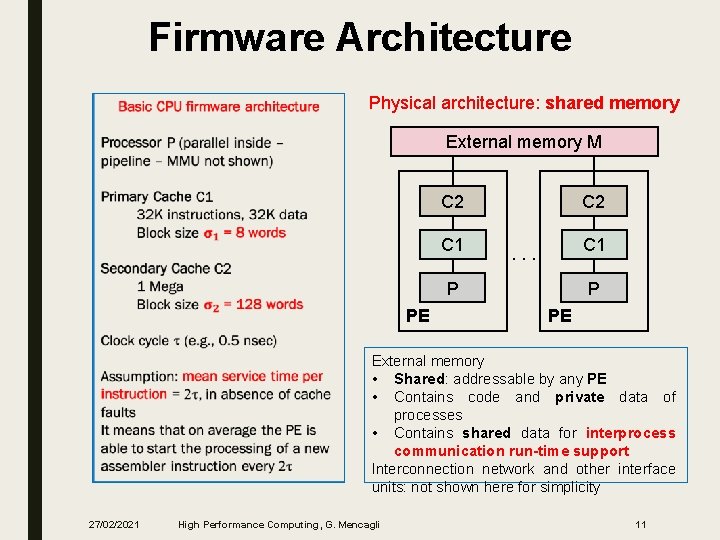
Firmware Architecture Physical architecture: shared memory External memory M C 2 C 1 . . . P PE External memory • Shared: addressable by any PE • Contains code and private data of processes • Contains shared data for interprocess communication run-time support Interconnection network and other interface units: not shown here for simplicity 27/02/2021 High Performance Computing, G. Mencagli 11

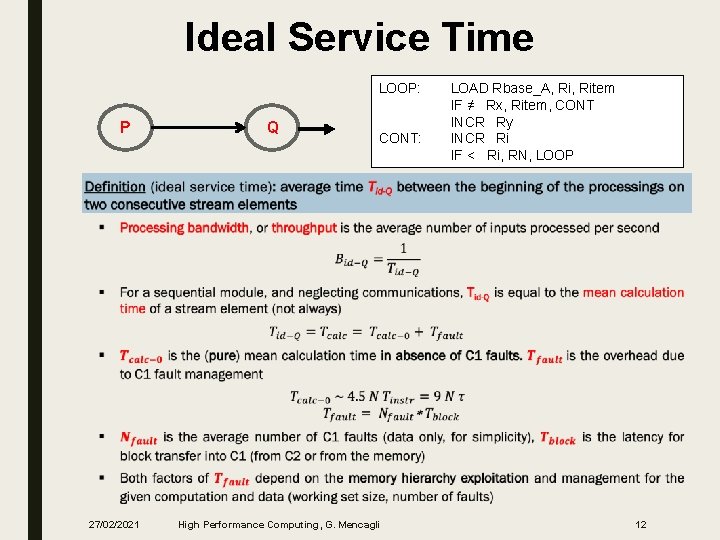
Ideal Service Time LOOP: P Q CONT: LOAD Rbase_A, Ritem IF ≠ Rx, Ritem, CONT INCR Ry INCR Ri IF < Ri, RN, LOOP 27/02/2021 High Performance Computing, G. Mencagli 12

Service Time and Caching (1) ■ 27/02/2021 High Performance Computing, G. Mencagli 13

Service Time and Caching (2) ■ 27/02/2021 High Performance Computing, G. Mencagli 14

Ideal and Effective Service Time § The service time evaluated till now is called ideal service time Tid-Q. It is the service time of process Q in isolation, independently of the whole computation S to which Q belongs P Q ■ 27/02/2021 High Performance Computing, G. Mencagli 15

Utilization Factor ■ 27/02/2021 High Performance Computing, G. Mencagli 16

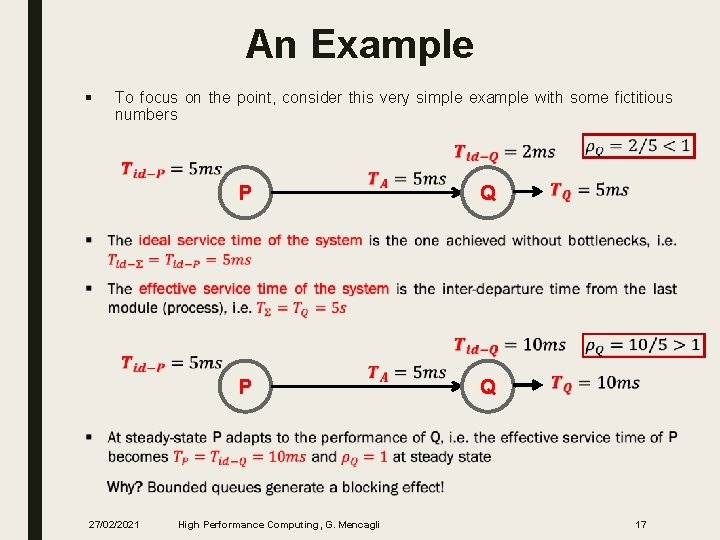
An Example § To focus on the point, consider this very simple example with some fictitious numbers P Q P Q 27/02/2021 High Performance Computing, G. Mencagli 17

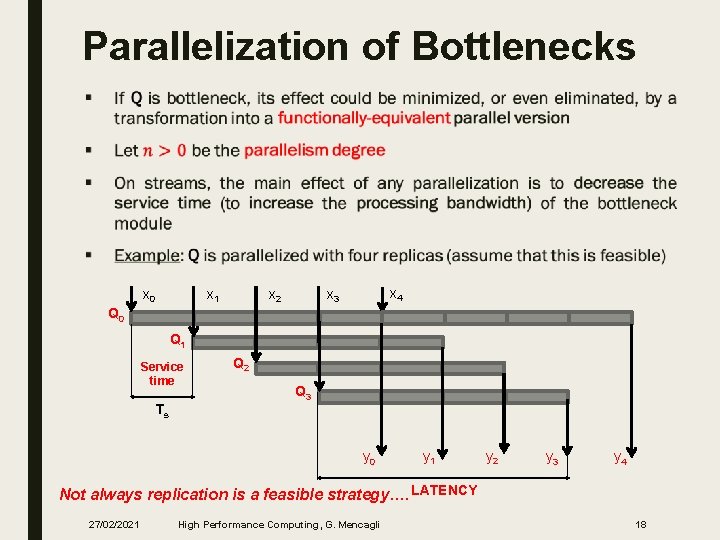
Parallelization of Bottlenecks ■ x 0 x 1 x 2 x 4 x 3 Q 0 Q 1 Service time Ts Q 2 Q 3 y 0 y 1 y 2 y 3 y 4 Not always replication is a feasible strategy…. LATENCY 27/02/2021 High Performance Computing, G. Mencagli 18

Functional Replication ■ 27/02/2021 High Performance Computing, G. Mencagli 19

Optimal Parallelism Degree ■ 27/02/2021 High Performance Computing, G. Mencagli 20

Parallelism Metrics 27/02/2021 High Performance Computing, G. Mencagli 21

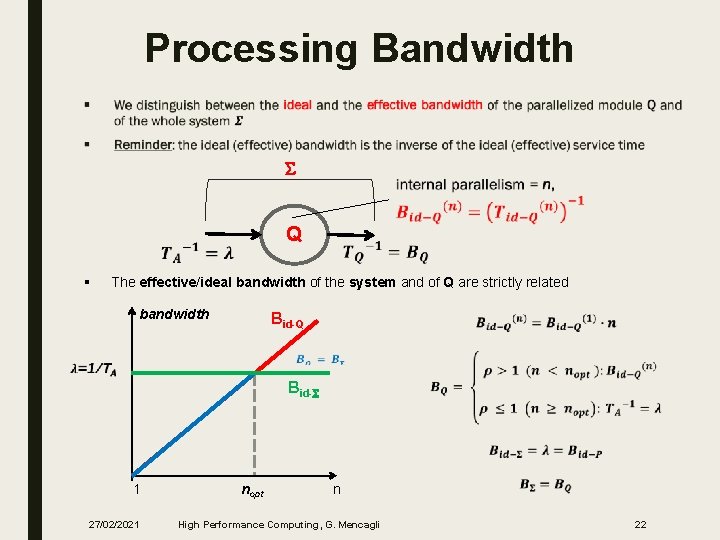
Processing Bandwidth ■ S Q § The effective/ideal bandwidth of the system and of Q are strictly related bandwidth Bid-Q Bid-S 1 27/02/2021 nopt n High Performance Computing, G. Mencagli 22

Completion Time ■ 27/02/2021 High Performance Computing, G. Mencagli 23

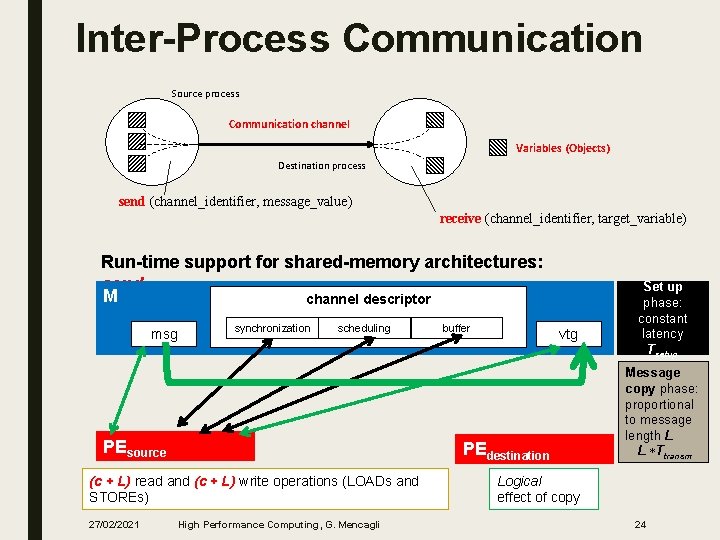
Inter-Process Communication Source process Communication channel Variables (Objects) Destination process send (channel_identifier, message_value) receive (channel_identifier, target_variable) Run-time support for shared-memory architectures: send M channel descriptor msg synchronization scheduling PEsource vtg PEdestination (c + L) read and (c + L) write operations (LOADs and STOREs) 27/02/2021 buffer High Performance Computing, G. Mencagli Set up phase: constant latency Tsetup Message copy phase: proportional to message length L L Ttransm Logical effect of copy 24

Communication Latency § In general, the inter-process communication latency can be expressed as 27/02/2021 High Performance Computing, G. Mencagli 25

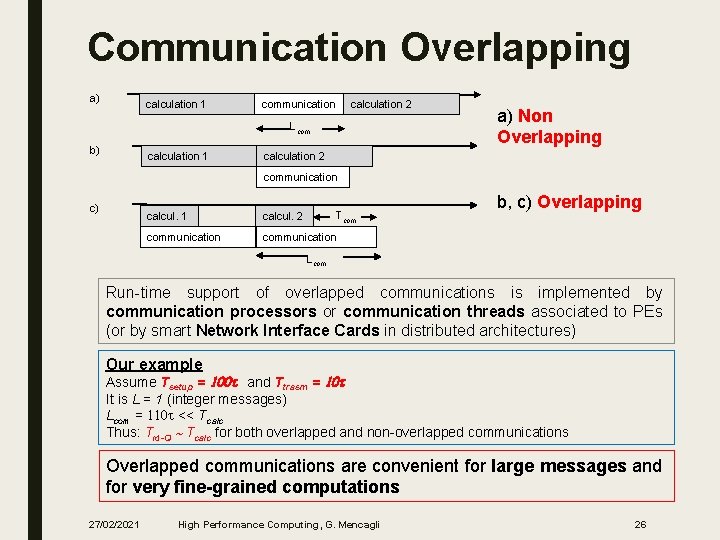
Communication Overlapping a) calculation 1 communication calculation 2 Lcom b) calculation 1 a) Non Overlapping calculation 2 communication c) Tcom calcul. 1 calcul. 2 communication b, c) Overlapping Lcom Run-time support of overlapped communications is implemented by communication processors or communication threads associated to PEs (or by smart Network Interface Cards in distributed architectures) Our example Assume Tsetup = 100 t and Ttrasm = 10 t It is L = 1 (integer messages) Lcom = 110 t << Tcalc Thus: Tid-Q Tcalc for both overlapped and non-overlapped communications Overlapped communications are convenient for large messages and for very fine-grained computations 27/02/2021 High Performance Computing, G. Mencagli 26

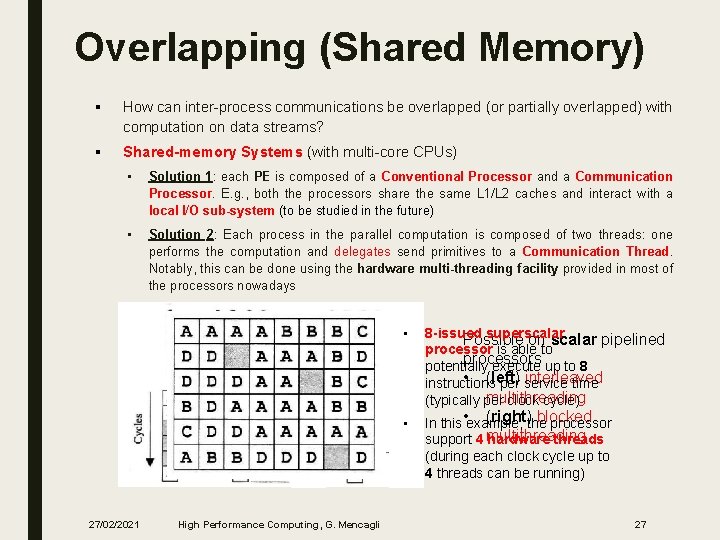
Overlapping (Shared Memory) § How can inter-process communications be overlapped (or partially overlapped) with computation on data streams? § Shared-memory Systems (with multi-core CPUs) • Solution 1: each PE is composed of a Conventional Processor and a Communication Processor. E. g. , both the processors share the same L 1/L 2 caches and interact with a local I/O sub-system (to be studied in the future) • Solution 2: Each process in the parallel computation is composed of two threads: one performs the computation and delegates send primitives to a Communication Thread. Notably, this can be done using the hardware multi-threading facility provided in most of the processors nowadays • • 27/02/2021 High Performance Computing, G. Mencagli 8 -issued superscalar Possible on scalar pipelined processor is able to processors potentially execute up to 8 • (left) interleaved instructions per service time multithreading (typically per clock cycle) • (right) blocked In this example, the processor support 4 multithreading hardware threads (during each clock cycle up to 4 threads can be running) 27

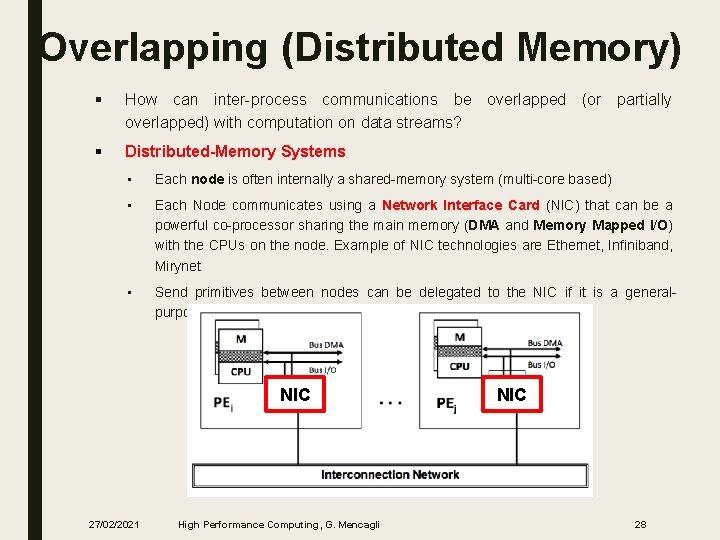
Overlapping (Distributed Memory) § How can inter-process communications be overlapped (or partially overlapped) with computation on data streams? § Distributed-Memory Systems • Each node is often internally a shared-memory system (multi-core based) • Each Node communicates using a Network Interface Card (NIC) that can be a powerful co-processor sharing the main memory (DMA and Memory Mapped I/O) with the CPUs on the node. Example of NIC technologies are Ethernet, Infiniband, Mirynet • Send primitives between nodes can be delegated to the NIC if it is a generalpurpose processor (“smart” NIC) NIC 27/02/2021 High Performance Computing, G. Mencagli NIC 28

Efficiency and Scalability P Q ■ Efficiency of a module (e. g. , Q) Efficiency of the system Theoretically, it grows until we reach the optimal bandwidth (i. e. the arrival rate) 27/02/2021 High Performance Computing, G. Mencagli 29

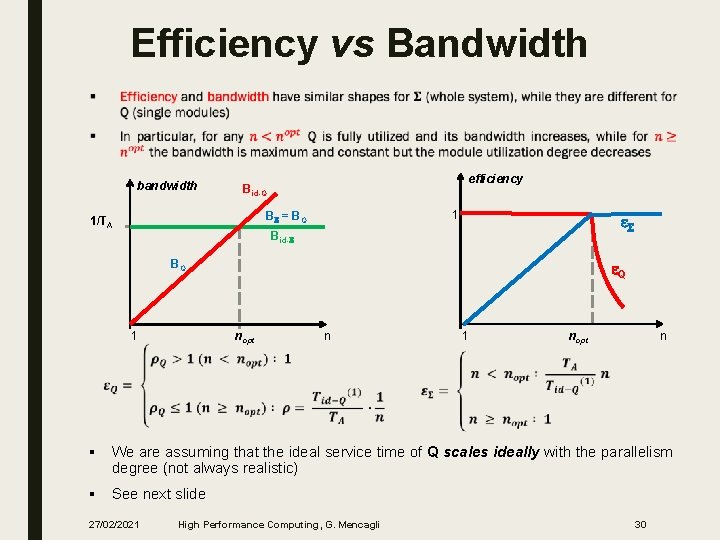
Efficiency vs Bandwidth ■ bandwidth efficiency Bid-Q 1 BS = BQ 1/TA e. S Bid-S BQ 1 e. Q nopt 1 n nopt n § We are assuming that the ideal service time of Q scales ideally with the parallelism degree (not always realistic) § See next slide 27/02/2021 High Performance Computing, G. Mencagli 30

Amdahl's Law ■ Note that here the problem size is fixed, and we vary the parallelism degree to reduce the execution time to solve the same problem size § If P is close to zero, theoretical limit of the scalability is roughly 1 (no benefit from parallelization) What about the previous example with a farm? Can you try to understand theoretical scalability limit in that case? 27/02/2021 High Performance Computing, G. Mencagli 31

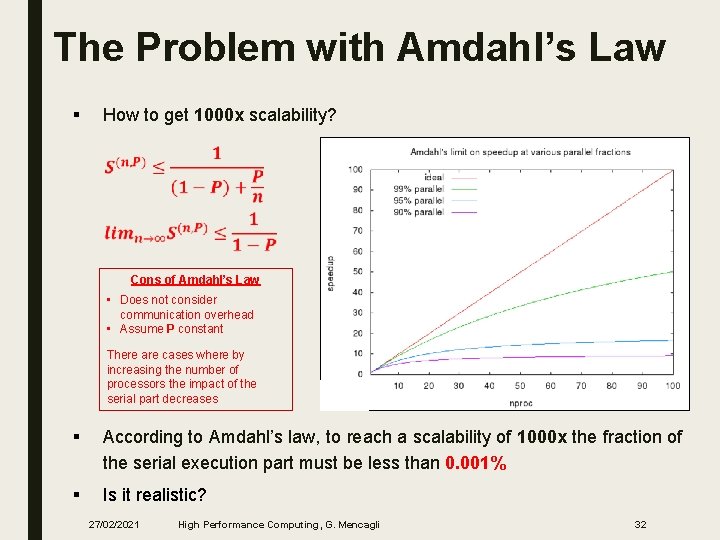
The Problem with Amdahl’s Law § How to get 1000 x scalability? Cons of Amdahl’s Law • Does not consider communication overhead • Assume P constant There are cases where by increasing the number of processors the impact of the serial part decreases § According to Amdahl’s law, to reach a scalability of 1000 x the fraction of the serial execution part must be less than 0. 001% § Is it realistic? 27/02/2021 High Performance Computing, G. Mencagli 32

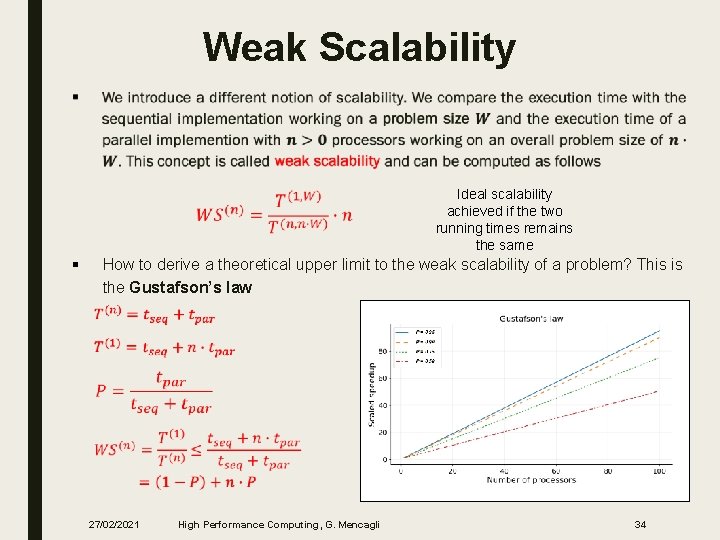
Gustafson's Law § Amdahl’s law gives the upper limit of scalability. In that case, we speak about strong scalability when we compare the execution time/service time of the sequential and the parallel version for the same problem size (input size) § However, if a problem is small (e. g. , it is its input) it might not be beneficial to use a large amount of resources to carry out the computation. It is natural to use more resources for bigger problems § Gustafson’s law (1988) is based on the approximation that the parallel part scales linearly with the amount of resources, and that the serial part does not increase with respect to the size of the problem 27/02/2021 High Performance Computing, G. Mencagli 33

Weak Scalability ■ § Ideal scalability achieved if the two running times remains the same How to derive a theoretical upper limit to the weak scalability of a problem? This is the Gustafson’s law 27/02/2021 High Performance Computing, G. Mencagli 34

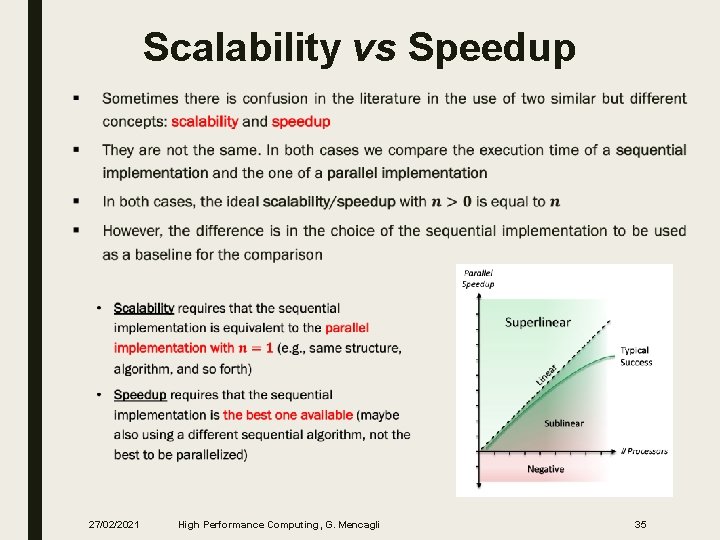
Scalability vs Speedup ■ 27/02/2021 High Performance Computing, G. Mencagli 35

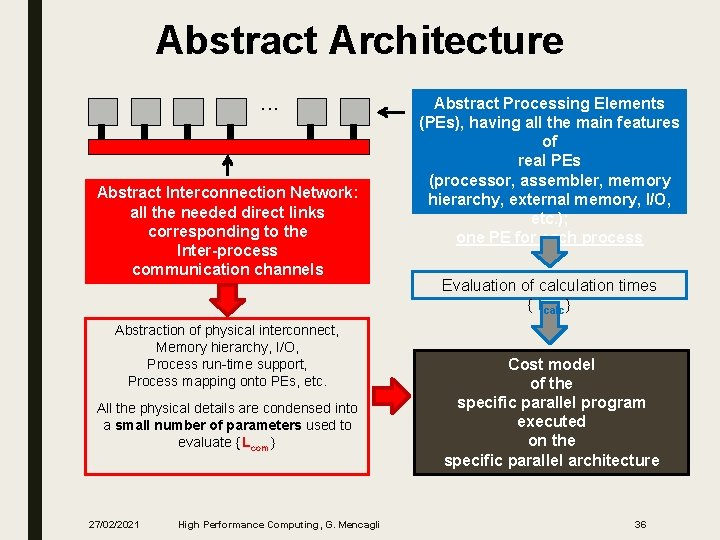
Abstract Architecture. . . Abstract Interconnection Network: all the needed direct links corresponding to the Inter-process communication channels Abstraction of physical interconnect, Memory hierarchy, I/O, Process run-time support, Process mapping onto PEs, etc. All the physical details are condensed into a small number of parameters used to evaluate Lcom 27/02/2021 High Performance Computing, G. Mencagli Abstract Processing Elements (PEs), having all the main features of real PEs (processor, assembler, memory hierarchy, external memory, I/O, etc. ); one PE for each process Evaluation of calculation times Tcalc Cost model of the specific parallel program executed on the specific parallel architecture 36