High leverage teaching learning practices for mathematics classrooms

High leverage teaching & learning practices for mathematics classrooms October 23, 2015 DANIELLE SEABOLD RESOURCES DANIELLE. SEABOLD@KRESA. ORG HTTP: //PADLET. COM/KALAMAZOORESA/TEACH

GOALS This morning, we will Begin to develop a common understanding of the high-level demands on learning our current standards dictate. Begin to develop a common understanding of which teaching and learning practices are critical in meeting these demands. Begin to develop comfort and skill in: a. Implementing the practices if you're a teach or coach. b. Looking for and supporting the practices if you're an administrator. My overall goal for the morning is for you to leave here interested and excited about deeply exploring 1 -2 high leverage teaching and learning practices with your colleagues back at your school or district.

LIKE ME Stand if you § Spend any part of your day teaching math § Are an administrator (building, district, or county) § Are a math coordinator or consultant § Are a general education educator § Are a special education educator § Are an instructional coach

GROUP NORMS FOR COLLABORATION Start and End on Time Pause, Paraphrase, and Probe Put Ideas on the Table Presume Positive Intentions Pay Attention to Self and Others Balance Advocacy and Inquiry DWELL IN POSSIBILITY

GROUNDING “The greatest impact on learning is the daily lived experiences of students in classrooms, and that is determined much more by how teachers teach than by what they teach. ” ~ Dylan William (2011)

HIGH LEVERAGE PRACTICES A “high-leverage practice” is an action or task central to teaching. Carried out skillfully, these practices increase the likelihood that teaching will be effective for students’ learning. They are useful across a broad range of subject areas, grade levels, and teaching contexts, and are helpful in using and managing differences among [students]. ~ Teaching Works, University of Michigan

WHY ARE WE HERE? THE MAGIC IS IN THE INSTRUCTION 1. Begin a lesson with a short review of previous learning 2. Present new material in small steps with student practice after each step 3. Ask a large number of questions and check the responses of all students 4. Provide models 5. Guide student practice 6. Check for student understanding 7. Obtain a high success rate 8. Provide scaffolds for difficult tasks 9. Require and monitor independent practice 10. Engage students in weekly and monthly review

WHY ARE WE HERE? WE CAN ENSURE THAT ALL STUDENT ACHIEVE AT HIGH LEVELS IN MATH 1. Focus: Focus strongly where the Standards focus. a. Critical Areas for each grade level b. Sequenced learning progressions 2. Coherence: Think across grades and link to major topics within grades. a. Sequenced learning progressions (across grades) b. Connections across Domains (within grades) 3. Rigor: In major topics, pursue conceptual understanding, procedural skill and fluency, and application. a. Begin with Conceptual Understanding to develop Procedural Skill b. Develop understanding and skill through problem solving

WHY ARE WE HERE? WE CAN ENSURE THAT ALL STUDENT ACHIEVE AT HIGH LEVELS IN MATH 1. Focus: Focus strongly where the Standards focus. a. Critical Areas for each grade level b. Sequenced learning progressions 2. Coherence: Think across grades and link to major topics within grades. a. Sequenced learning progressions (across grades) b. Connections across Domains (within grades) 3. Rigor: In major topics, pursue conceptual understanding, procedural skill and fluency, and application. a. Begin with Conceptual Understanding to develop Procedural Skill b. Develop understanding and skill through problem solving

WHY ARE WE HERE? WE CAN ENSURE THAT ALL STUDENT ACHIEVE AT HIGH LEVELS IN MATH 1. Focus: Focus strongly where the Standards focus. a. Critical Areas for each grade level b. Sequenced learning progressions 2. Coherence: Think across grades and link to major topics within grades. a. Sequenced learning progressions (across grades) b. Connections across Domains (within grades) 3. Rigor: In major topics, pursue conceptual understanding, procedural skill and fluency, and application. a. Begin with Conceptual Understanding to develop Procedural Skill b. Develop understanding and skill through problem solving

WHY ARE WE HERE? WE CAN ENSURE THAT ALL STUDENT ACHIEVE AT HIGH LEVELS IN MATH 1. Focus: Focus strongly where the Standards focus. a. Critical Areas for each grade level b. Sequenced learning progressions 2. Coherence: Think across grades and link to major topics within grades. a. Sequenced learning progressions (across grades) b. Connections across Domains (within grades) 3. Rigor: In major topics, pursue conceptual understanding, procedural skill and fluency, and application. a. Begin with Conceptual Understanding to develop Procedural Skill b. Develop understanding and skill through problem solving

EVIDENCE ALL STUDENTS ACHIEVING AT HIGH LEVELS IN MATH What does it look like when a 2 nd grader has developed procedural skill from conceptual understanding? In your head, sum 69 and 87. After you’ve found the sum, jot down key points of your solution strategy. Next, share your sum and solution strategy with your shoulder partner.

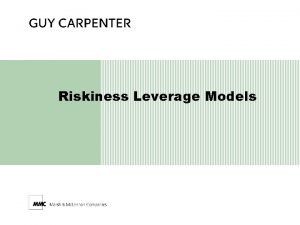
Rigor Activity: Analyzing Sample Problems http: //achievethecore. org/page/400/introduction-to-the-shifts-pd-module#three-activities-focus-coherence-andrigor RIGOR: CONCEPTUAL UNDERSTANDING

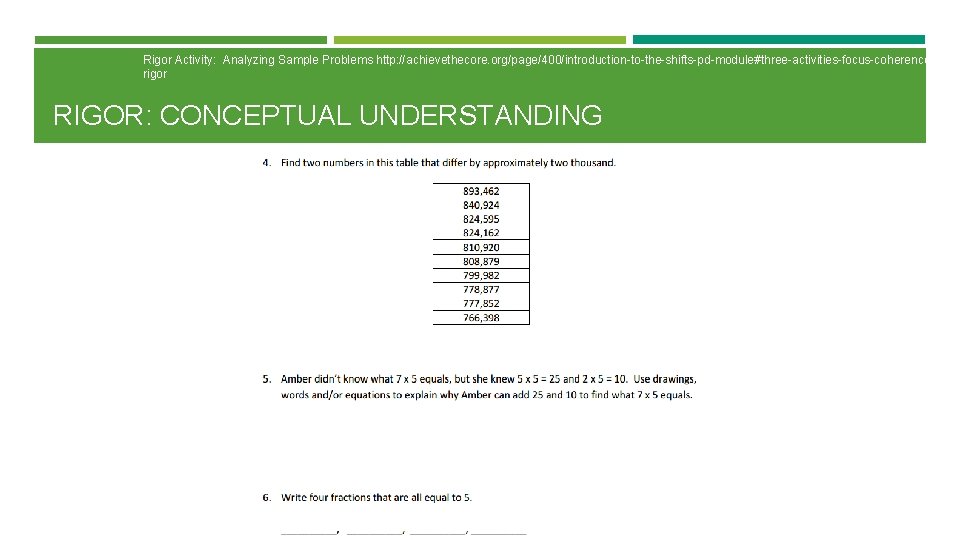
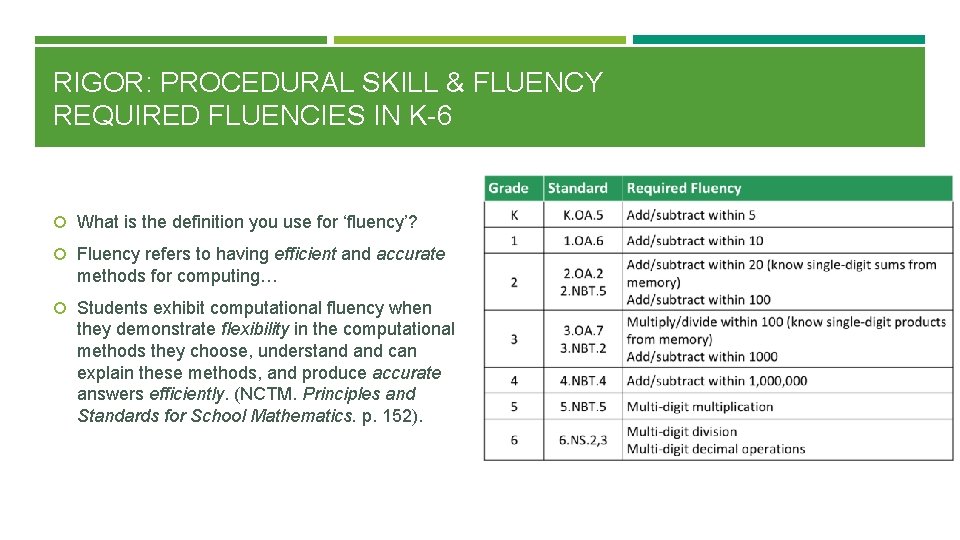
RIGOR: PROCEDURAL SKILL & FLUENCY REQUIRED FLUENCIES IN K-6 What is the definition you use for ‘fluency’? Fluency refers to having efficient and accurate methods for computing… Students exhibit computational fluency when they demonstrate flexibility in the computational methods they choose, understand can explain these methods, and produce accurate answers efficiently. (NCTM. Principles and Standards for School Mathematics. p. 152).

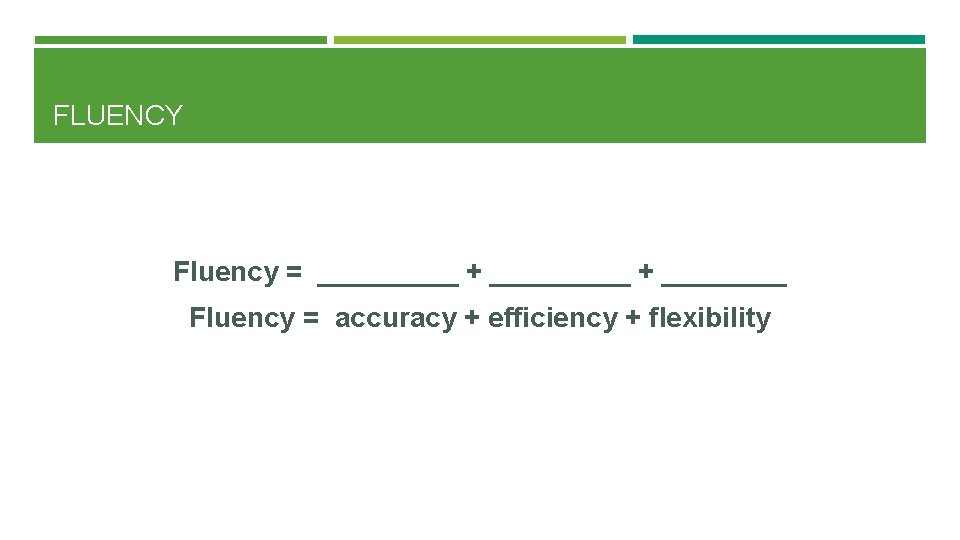
FLUENCY Fluency = _________ + ____ Fluency = accuracy + efficiency + flexibility

Rigor Activity: Analyzing Sample Problems http: //achievethecore. org/page/400/introduction-to-the-shifts-pd-module#three-activities-focus-coherence-andrigor RIGOR: PROCEDURAL SKILL & FLUENCY

Rigor Activity: Analyzing Sample Problems http: //achievethecore. org/page/400/introduction-to-the-shifts-pd-module#three-activities-focus-coherence-andrigor RIGOR: APPLICATION

STANDARDS FOR MATHEMATICAL PRACTICE ALL STUDENTS ACHIEVING AT HIGH LEVELS IN MATH The Common Core Standards for Mathematics come in two parts—the Content Standards which describe what is taught in each grade or course, and the Standards for Mathematical Practice which describe eight areas of expertise that students should develop over the course of their school math careers: 1. Make sense of problems and persevere in solving them. 2. Reason abstractly and quantitatively. 3. Construct viable arguments and critique the reasoning of others. 4. Model with mathematics. 5. Use appropriate tools strategically. 6. Attend to precision. 7. Look for and make use of structure. 8. Look for and express regularity in repeated reasoning.

HIGH-QUALITY STANDARDS ARE NECESSARY FOR EFFECTIVE TEACHING AND LEARNING, BUT INSUFFICIENT The Common Core does not describe or prescribe the essential conditions required to make sure mathematics works for all students.

PRINCIPLES TO ACTIONS: ENSURING MATHEMATICAL SUCCESS FOR ALL The primary purpose of Principles to Actions is to fill the gap between the adoption of rigorous standards and the enactment of practices, policies, programs, and actions required for successful implementation of those standards. The overarching message is that effective teaching is the non-negotiable core necessary to ensure that all students learn mathematics.

GUIDING PRINCIPLES FOR SCHOOL MATHEMATICS 1. Teaching and Learning 2. Access and Equity 3. Curriculum 4. Tools and Technology 5. Assessment 6. Professionalism Essential Elements of Effective Mathematics Programs

TEACHING AND LEARNING PRINCIPLE An excellent mathematics program requires effective teaching that engages students in meaningful learning through individual and collaborative experiences that promote their ability to make sense of mathematical ideas and reason mathematically. Effective teaching is the non-negotiable core that ensures that all students learn mathematics at high levels.

WE MUST FOCUS ON HIGH-LEVERAGE INSTRUCTIONAL PRACTICES Student learning of mathematics “depends fundamentally on what happens inside the classroom as teachers and learners interact over the curriculum. ” (Ball & Forzani, 2011, p. 17) “Teaching has 6 to 10 times as much impact on achievement as all other factors combined. . . Just three years of effective teaching accounts on average for an improvement of 35 to 50 percentile points. ” (Schmoker, 2006, p. 9)

GETTING STARTED: OBSTACLES TO IMPLEMENTING HIGH LEVERAGE INSTRUCTIONAL PRACTICES Dominant cultural beliefs about the teaching and learning of mathematics continue to be obstacles to consistent implementation of effective teaching and learning in mathematics classrooms. With your shoulder partner, examine the belief statements about teaching and learning math. Select the most productive and the least productive belief you can find.

HIGH LEVERAGE TEACHING & LEARNING PRACTICES Principles to Actions: Teaching & Learning Practices 1. Establish mathematics goals to focus learning 2. Implement tasks that promote reasoning and problem solving 3. Use and connect mathematical representations 4. Facilitate meaningful mathematical discourse 5. Pose purposeful questions 6. Build procedural fluency from conceptual understanding 7. Support productive struggle in learning mathematics 8. Elicit and use evidence of student thinking

HIGH LEVERAGE TEACHING & LEARNING PRACTICES Principles of Instruction Principles to Actions: Teaching & Learning Practices 1. Begin a lesson with a short review of previous learning 1. Establish mathematics goals to focus learning 2. Present new material in small steps with student practice after each step 2. 3. Ask a large number of questions and check the responses of all students Implement tasks that promote reasoning and problem solving 3. Use and connect mathematical representations 4. Provide models Guide student practice 4. Facilitate meaningful mathematical discourse 5. 6. Check for student understanding 5. Pose purposeful questions 7. Obtain a high success rate 6. Build procedural fluency from conceptual understanding 8. Provide scaffolds for difficult tasks 7. Support productive struggle in learning mathematics 9. Require and monitor independent practice 8. Elicit and use evidence of student thinking 10. Engage students in weekly and monthly review

1. ESTABLISH MATHEMATICS GOALS TO FOCUS LEARNING Effective teaching of mathematics establishes clear goals for the mathematics that students are learning, situates goals within learning progressions, and uses goals to guide instructional decisions. Learning Goals should Clearly state what it is students are to learn and understand about mathematics as the result of instruction; Be situated within learning progressions; and Frame the decisions that teachers make during a lesson. Formulating clear, explicit learning goals sets the stage for everything else. (Hiebert, Morris, Berk, & Janssen, 2007, p. 57)

ESTABLISHING A PRODUCTIVE CLASSROOM CULTURE & CLIMATE FOR LEARNING: PREPARING TO INTERACT WITH LEARNING GOALS Anyone can do well in math

ESTABLISHING A PRODUCTIVE CLASSROOM CULTURE & CLIMATE FOR LEARNING: PREPARING TO INTERACT WITH LEARNING GOALS Classroom norms Norms are agreements between teachers and students that help set the classroom climate and culture. Make classroom norms explicit. Set the norms together; with teacher guidance. ~ Classroom Norms provided by Jo Boaler

1. ESTABLISH MATHEMATICS GOALS TO FOCUS LEARNING: LOOK FORS As you examine the look fors, identify one thing you’re already doing (daily) you want to start doing (or do more consistently) Next, discuss what you have in place and what you will put in place for this Practice.

2. IMPLEMENT TASKS THAT PROMOTE REASONING AND PROBLEM SOLVING Effective teaching of mathematics engages students in solving and discussing tasks that promote mathematical reasoning and problem solving and that allow for multiple entry points and varied solution strategies. Mathematical tasks should: Provide opportunities for students to engage in exploration or encourage students to use procedures in ways that are connected to concepts and understanding; Build on students’ current understanding; and Have multiple entry points. There is no decision that teachers make that has a greater impact on students’ opportunities to learn and on their perceptions about what mathematics is than the selection or creation of the tasks with which the teacher engages students in studying mathematics. (Lappan & Briars, 1995)

2. IMPLEMENT TASKS THAT PROMOTE REASONING AND PROBLEM SOLVING: TASK SELECTION Lower-level cognitive demand Higher-level cognitive demand Memorization What is the rule for multiplying fractions? Procedures with Connections Find 1/6 of 1/2. Use pattern blocks. Draw your answer and explain your solution. Stein, Mary kay, and Margaret S. Smith. “Mathematical Tasks as a Framework for Reflections: From Research to Practice. ” Mathematics Teaching in the Middle School 3, no. 4 (1998): 268 -75

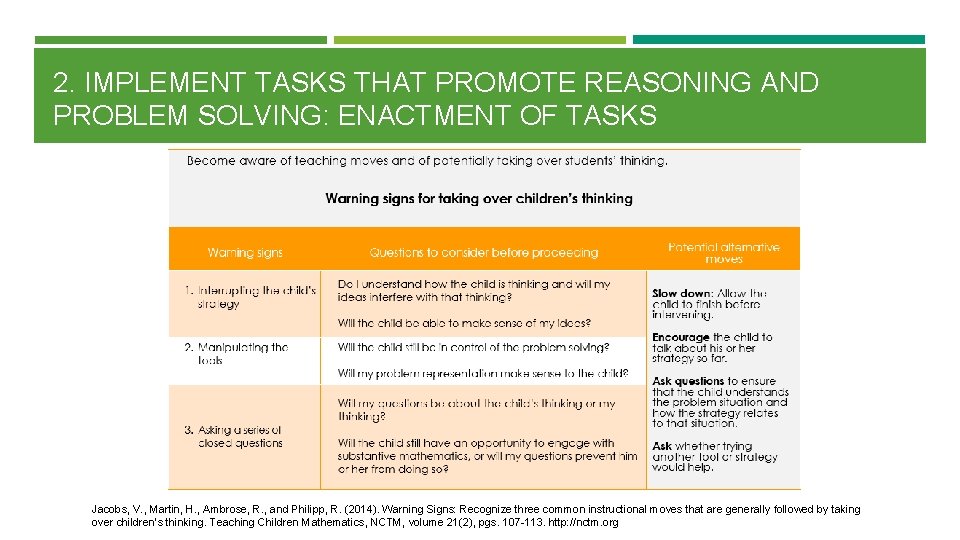
2. IMPLEMENT TASKS THAT PROMOTE REASONING AND PROBLEM SOLVING: ENACTMENT OF TASKS Jacobs, V. , Martin, H. , Ambrose, R. , and Philipp, R. (2014). Warning Signs: Recognize three common instructional moves that are generally followed by taking over children’s thinking. Teaching Children Mathematics, NCTM, volume 21(2), pgs. 107 -113. http: //nctm. org

2. IMPLEMENT TASKS THAT PROMOTE REASONING AND PROBLEM SOLVING: LOOK FORS As you examine the look fors, identify one thing you’re already doing (daily) you want to start doing (or do more consistently) Next, discuss what you have in place and what you will put in place for this Practice.

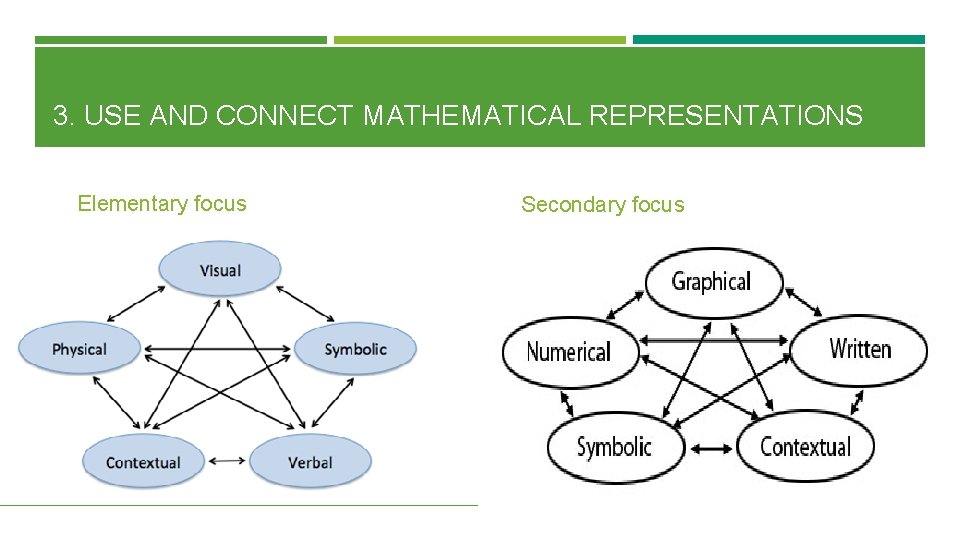
3. USE AND CONNECT MATHEMATICAL REPRESENTATIONS Effective teaching of mathematics engages students in making connections among mathematical representations to deepen understanding of mathematics concepts and procedures and as tools for problem solving. Different Representations should: Be introduced, discussed, and connected; Focus students’ attention on the structure or essential features of mathematical ideas; and Support students’ ability to justify and explain their reasoning. Strengthening the ability to move between and among these representations improves the growth of children’s concepts. (Lesh, Post, Behr, 1987)

3. USE AND CONNECT MATHEMATICAL REPRESENTATIONS Elementary focus Secondary focus

CONCRETE-REPRESENTATION-ABSTRACT (CRA) LEARNING SEQUENCE Concrete (Objects) • Manipulatives including • Two-color counters • Base ten blocks or cubes (connecting) • Physical number line Representation al (drawings) • Pictures or drawings including • Area/Array Models • Drawing cubes or base ten blocks • Number line, 100 s chart, place value mat, ten frames Abstract (equations) • Equations derived from objects and pictures including • a x b = c AND c = a x b • a x b = c AND a = c ÷ b OR b = c ÷ a • a = b + c + d

3. USE AND CONNECT MATHEMATICAL REPRESENTATIONS: LOOK FORS As you examine the look fors, identify one thing you’re already doing (daily) you want to start doing (or do more consistently) Next, discuss what you have in place and what you will put in place for this Practice.

4. FACILITATE MEANINGFUL MATHEMATICAL DISCOURSE Effective teaching of mathematics facilitates discourse among students in order to build shared understanding of mathematical ideas by analyzing and comparing student approaches and arguments. Mathematical Discourse should: Build on and honor students’ thinking; Provide students with the opportunity to share ideas, clarify understandings, and develop convincing arguments; and Advance the mathematical learning of the whole class. Discussions that focus on cognitively challenging mathematical tasks, namely those that promote thinking, reasoning, and problem solving, are a primary mechanism for promoting conceptual understanding of mathematics (Hatano & Inagaki, 1991; Michaels, O’Connor, & Resnick, 2008)

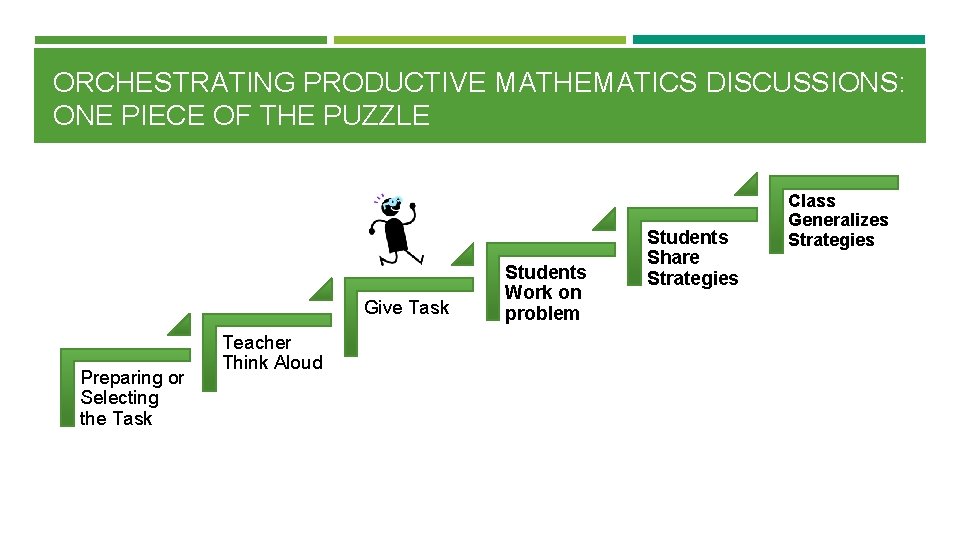
ORCHESTRATING PRODUCTIVE MATHEMATICS DISCUSSIONS 1. Anticipating student response prior to the lesson 2. Monitoring students’ work on and engagement with the tasks 3. Selecting particular students to present their mathematical work 4. Sequencing student responses in a specific order for discussion 5. Connecting different student‘s’ responses and connecting the responses to key mathematical ideas

ORCHESTRATING PRODUCTIVE MATHEMATICS DISCUSSIONS: ONE PIECE OF THE PUZZLE Give Task Preparing or Selecting the Task Teacher Think Aloud Students Work on problem Students Share Strategies Class Generalizes Strategies

4. FACILITATE MEANINGFUL MATHEMATICAL DISCOURSE: LOOK FORS As you examine the look fors, identify one thing you’re already doing (daily) you want to start doing (or do more consistently) Next, discuss what you have in place and what you will put in place for this Practice.

5. POSE PURPOSEFUL QUESTIONS Effective teaching of mathematics uses purposeful questions to assess and advance student reasoning and sense making about important mathematical ideas and relationships. Effective Questions should: Reveal students’ current understandings; Encourage students to explain, elaborate, or clarify their thinking; and Make the mathematics more visible and accessible for student examination and discussion. Teachers’ questions are crucial in helping students make connections and learn important mathematics and science concepts. Teachers need to know how students typically think about particular concepts, how to determine what a particular student or group of students thinks about those ideas, and how to help students deepen their understanding. (Weiss & Pasley, 2004)

WHY FOCUS ON POSING PURPOSEFUL QUESTIONS? “About 60% of teachers' questions require students to recall facts; about 20% require students to think; and the remaining 20% are procedural. ” -Meredith D. Gall; Source: http: //files. eric. ed. gov/fulltext/ED 067650. pdf

WHY FOCUS ON POSING PURPOSEFUL QUESTIONS? The impact of instruction on student learning is determined, in part, by the quality of questions that we ask students. Our questions should explore mathematical meanings and relationships probe to get students to explain their thinking generate discussion They should not be limited to those questions that gather information and lead students through a procedure.

QUESTIONING CHALLENGES Teacher challenges: It is difficult to spontaneously come up with questions that will challenge students to make connections without simply telling them what to do. Student challenges: Students have been trained to believe that teachers only care about the answer to the problem, not how they thought about it. It takes time for students to adjust to explaining themselves and the idea of discussing the problem will seem foreign to them at first. Robert Kaplinsky, Robert. Kaplinsky. com

WHY FOCUS ON POSING PURPOSEFUL QUESTIONS? “About 60% of teachers' questions require students to recall facts; about 20% require students to think; and the remaining 20% are procedural. ” -Meredith D. Gall; Source: http: //files. eric. ed. gov/fulltext/ED 067650. pdf

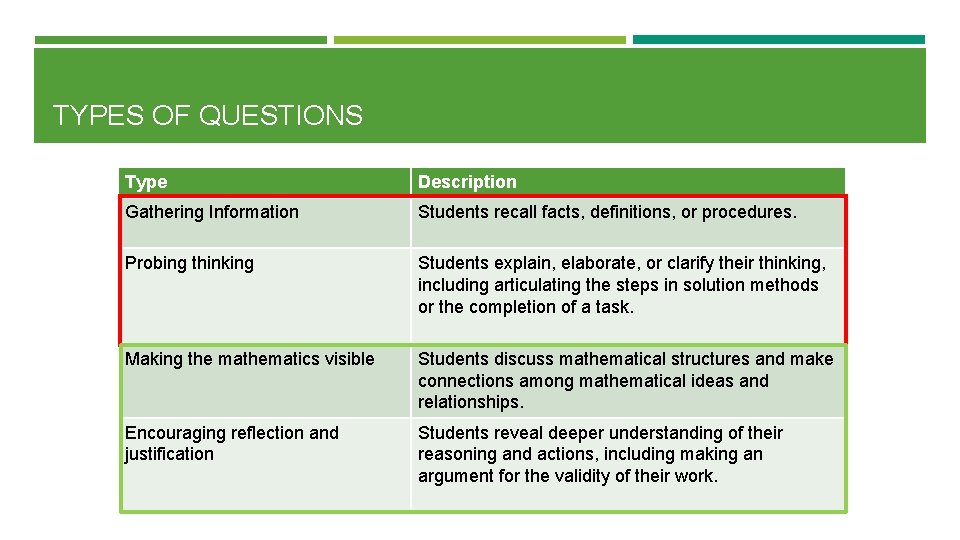
TYPES OF QUESTIONS Type Description Gathering Information Students recall facts, definitions, or procedures. Probing thinking Students explain, elaborate, or clarify their thinking, including articulating the steps in solution methods or the completion of a task. Making the mathematics visible Students discuss mathematical structures and make connections among mathematical ideas and relationships. Encouraging reflection and justification Students reveal deeper understanding of their reasoning and actions, including making an argument for the validity of their work.

SELECTING PURPOSEFUL QUESTIONS Ponder each and then give examples Which questions are those you routinely ask your students? Which questions will help make mathematics visible? Which questions will help to probe thinking? Which questions will help to encourage reflection and justification?

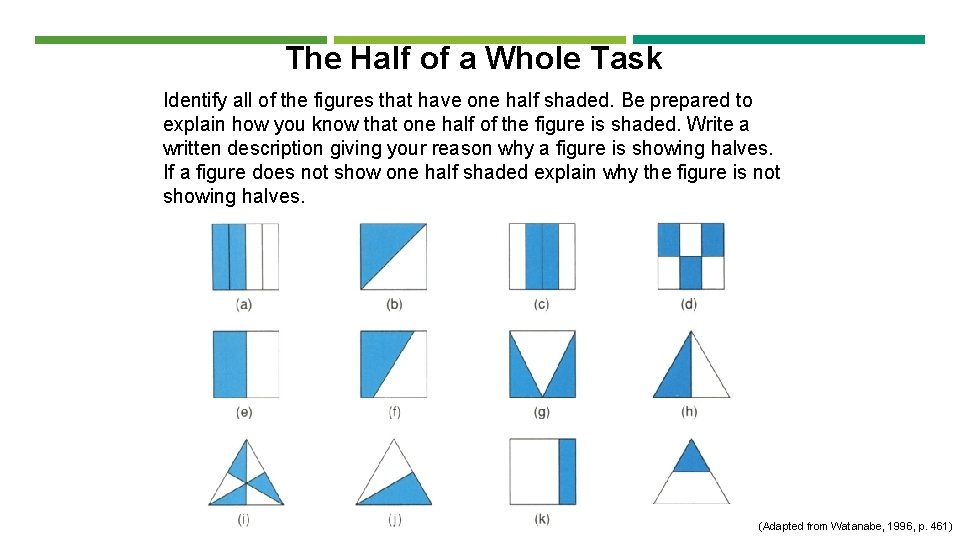
The Half of a Whole Task Identify all of the figures that have one half shaded. Be prepared to explain how you know that one half of the figure is shaded. Write a written description giving your reason why a figure is showing halves. If a figure does not show one half shaded explain why the figure is not showing halves. (Adapted from Watanabe, 1996, p. 461)

THE HALF OF A WHOLE TASK What do students need to know and be able to do in order to engage with the task? What mathematical ideas does the task provide an opportunity for students to learn?

MS. BROOKS’ MATHEMATICS LEARNING GOALS Students will understand that: A fraction describes the division of a whole region or area into equal parts. A fraction is relative to the size of the whole unit. If the numerator is half the quantity in the denominator then the fraction is equal to a half. Fractions have an infinite number of equivalent forms, regardless of whether or not the pieces of the whole unit are adjacent.

CONNECTIONS TO THE CCSSM GRADE 3 STANDARDS FOR MATHEMATICAL CONTENT Number and Operations – Fractions (NF) Develop understanding of fractions as numbers. 3. NF. A. Understand a fraction 1/b as the quantity formed by 1 part when a whole is 1 partitioned into b equal parts; understand a fraction a/b as the quantity formed by a parts of size 1/b. 3. NF. A. Explain equivalence of fractions in special cases, and compare fractions by 3 reasoning about their size. (a) Understand two fractions as equivalent (equal) if they are the same size, or the same point on a number line. (b) Recognize and generate simple equivalent fractions (e. g. , 1/2=2/4, 4/6=2/3). Explain why the fractions are equivalent, e. g. , by using a visual fraction model. National Governors Association Center for Best Practices (NGA Center) and Council of Chief State School Officers (CCSSO). (2014). Common core state standards for mathematics. http: //www. corestandards. org/Math/Content/3/NF

CONNECTIONS TO THE CCSSM STANDARDS FOR MATHEMATICAL PRACTICE Make sense of problems and persevere in solving them. Reason abstractly and quantitatively. Construct viable arguments and critique the reasoning of others. Model with mathematics. Use appropriate tools strategically. Attend to precision. Look for and make use of structure. Look for and express regularity in repeated reasoning.

CONTEXT OF THE VIDEO CLIP Teacher: Millie Brooks Grade: 3 School: #26 District: Paterson Public Schools This lesson takes place in February. Students have just begun their study of fractions. After reading the instructions aloud, Ms. Brooks asked students to work on the task in small groups. The clip shows the interactions that Ms. Brooks had with one of the small groups, in which there was a disagreement about Figure (d).

LENS FOR WATCHING THE VIDEO As you watch the video clip, make note of: The ways in which Ms. Brooks facilitated meaningful mathematical discourse, and The questions asked by Ms. Brooks. Be prepared to give examples and to cite line numbers from the transcript to support your observations.

5. POSE PURPOSEFUL QUESTIONS: LOOK FORS As you examine the look fors, identify one thing you’re already doing (daily) you want to start doing (or do more consistently) Next, discuss what you have in place and what you will put in place for this Practice.

6. BUILD PROCEDURAL FLUENCY FROM CONCEPTUAL UNDERSTANDING Effective teaching of mathematics builds fluency with procedures on a foundation of conceptual understanding so that students, over time, become skillful in using procedures flexibly as they solve contextual and mathematical problems. Procedural Fluency should: Build on a foundation of conceptual understanding; Result in generalized methods for solving problems; and Enable students to flexibly choose among methods to solve contextual and mathematical problems. Students must be able to do much more than carry out mathematical procedures. They must know which procedure is appropriate and most productive in a given situation, what a procedure accomplishes, and what kind of results to expect. Mechanical execution of procedures without understanding their mathematical basis often leads to bizarre results. (Martin, 2009, p. 165)

Fluency = Accuracy + Efficiency + Flexibility

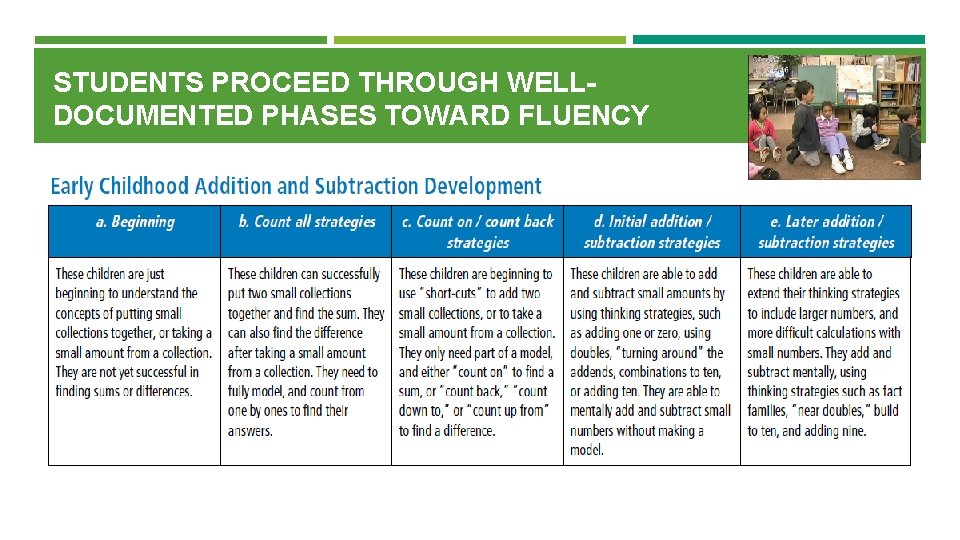
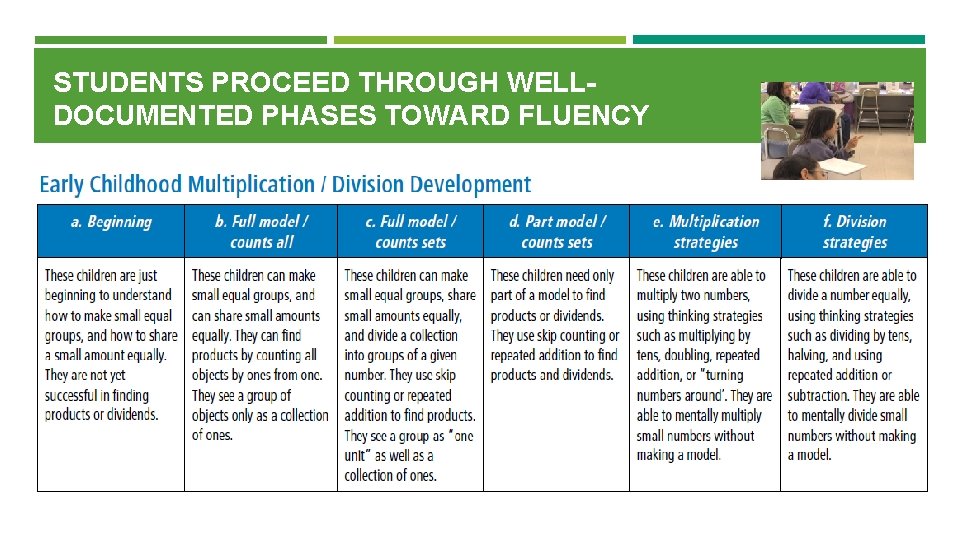
Guiding Principles: Build procedural fluency from conceptual understanding Effective teaching of mathematics builds fluency with procedures on a foundation of conceptual solve understanding so that students, over time, become skillful in using procedures flexibly as they contextual and mathematical problems. Being fluent means that students are able to choose flexibly among methods and strategies to solve contextual and mathematical problems, they understand are able to explain their approaches, and they are able to produce accurate answers efficiently. 1 When procedures are connected with the underlying concepts, students have better retention of the procedures and are more able to apply them in new situations. A rush to fluency undermines students’ confidence and interest in mathematics and is considered a cause of mathematics anxiety. 2 Students proceed through well-documented phases toward fluency. Students begin by using objects, visual representations, and verbal counting, and then they progress to reasoning strategies using number relationships and properties. 3 Standard algorithms are to be understood and explained and related to visual models before there is any focus on fluency. 4 When teachers provide students with practice on a small number of problems, “spacing” or distributing these over time, and include feedback on student performance, students become fluent. Practice should be brief, engaging, purposeful, and distributed.

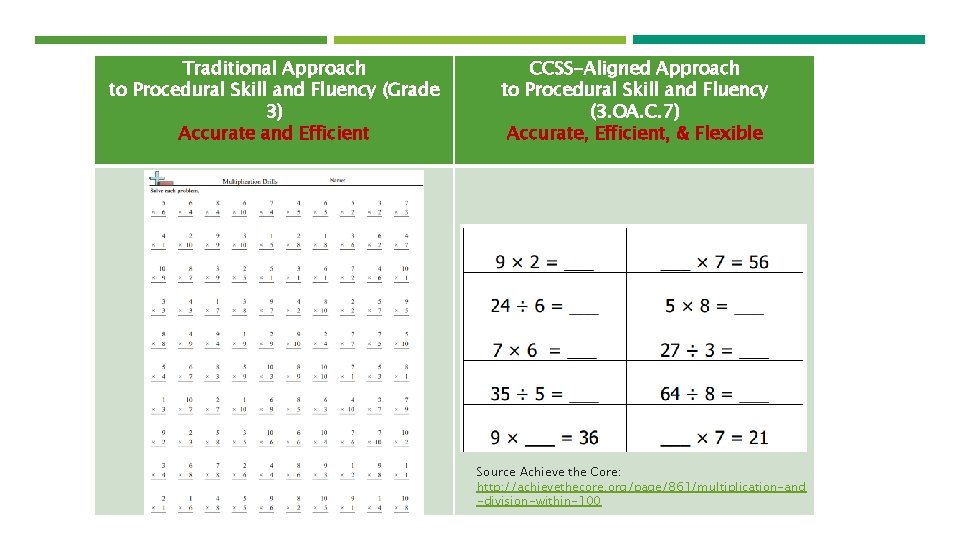
Traditional Approach to Procedural Skill and Fluency (Grade 3) Accurate and Efficient CCSS-Aligned Approach to Procedural Skill and Fluency (3. OA. C. 7) Accurate, Efficient, & Flexible Source Achieve the Core: http: //achievethecore. org/page/861/multiplication-and -division-within-100

STUDENTS PROCEED THROUGH WELLDOCUMENTED PHASES TOWARD FLUENCY

STUDENTS PROCEED THROUGH WELLDOCUMENTED PHASES TOWARD FLUENCY

6. BUILD PROCEDURAL FLUENCY FROM CONCEPTUAL UNDERSTANDING: LOOK FORS As you examine the look fors, identify one thing you’re already doing (daily) you want to start doing (or do more consistently) Next, discuss what you have in place and what you will put in place for this Practice.

7. SUPPORT PRODUCTIVE STRUGGLE IN LEARNING MATHEMATICS Effective teaching of mathematics consistently provides students, individually and collectively, with opportunities and supports to engage in productive struggle as they grapple with mathematical ideas and relationships. Productive Struggle should: Be considered essential to learning mathematics with understanding; Develop students’ capacity to persevere in the face of challenge; and Help students realize that they are capable of doing well in mathematics with effort. The struggle we have in mind comes from solving problems that are within reach and grappling with key mathematical ideas that are comprehendible but not yet well formed (Hiebert et al. , 1996). By struggling with important mathematics we mean the opposite of simply being presented information to be memorized or being asked only to practice what has been demonstrated. (Hiebert & Grouws, 2007, pp. 387 -388)

SUPPORT PRODUCTIVE STRUGGLE: ANALYZING STUDENT WORK Expectations for students Teacher actions to support students Classroom-based indicators of success Most tasks that promote reasoning and problem solving take time to solve, and frustration may occur, but perseverance in the face of initial difficulty is important. Using tasks that promote reasoning and problem solving; explicitly encourage students to persevere; find ways to support students without removing all the challenges in a task. Students are engaged in the tasks and do not give up. The teacher supports students when they are “stuck” but does so in a way that keeps the thinking and reasoning at a high level. Correct solutions are important, but so is being able to explain and discuss how one thought about and solved particular tasks. Ask students to explain and justify how they solved a task. Value the quality of the explanation as much as the final solution. Students explain how they solved a task and provide mathematical justifications for their reasoning. Everyone has a responsibility and an obligation to make sense of mathematics by asking questions of peers and the teacher when he or she does not understand. Give students the opportunity to discuss and determine the validity and appropriateness of strategies and solutions. Students question and critique the reasoning of their peers and reflect on their own understanding.

If your students are going home at the end of the day less tired than you are, the division of labor in your classroom requires some attention. Wiliam, D. (2011)

7. SUPPORT PRODUCTIVE STRUGGLE IN LEARNING MATHEMATICS: LOOK FORS As you examine the look fors, identify one thing you’re already doing (daily) you want to start doing (or do more consistently) Next, discuss what you have in place and what you will put in place for this Practice.

8. ELICIT AND USE EVIDENCE OF STUDENT THINKING Effective teaching of mathematics uses evidence of student thinking to assess progress toward mathematical understanding and to adjust instruction continually in ways that support and extend learning. Evidence should: Provide a window into students’ thinking; Help the teacher determine the extent to which students are reaching the math learning goals; and Be used to make instructional decisions during the lesson and to prepare for subsequent lessons. Formative assessment is an essentially interactive process, in which the teacher can find out whether what has been taught has been learned, and if not, to do something about it. Day-to-day formative assessment is one of the most powerful ways of improving learning in the mathematics classroom. (Wiliam, 2007, pp. 1054; 1091)

8. ELICIT AND USE EVIDENCE OF STUDENT THINKING “direct modeling” “counting on/back” “derived facts”

8. ELICIT AND USE EVIDENCE OF STUDENT THINKING: LOOK FORS As you examine the look fors, identify one thing you’re already doing (daily) you want to start doing (or do more consistently) Next, discuss what you have in place and what you will put in place for this Practice.

HIGH LEVERAGE TEACHING & LEARNING PRACTICES Principles to Actions: Teaching & Learning Practices 1. Establish mathematics goals to focus learning 2. Implement tasks that promote reasoning and problem solving 3. Use and connect mathematical representations 4. Facilitate meaningful mathematical discourse 5. Pose purposeful questions 6. Build procedural fluency from conceptual understanding 7. Support productive struggle in learning mathematics 8. Elicit and use evidence of student thinking

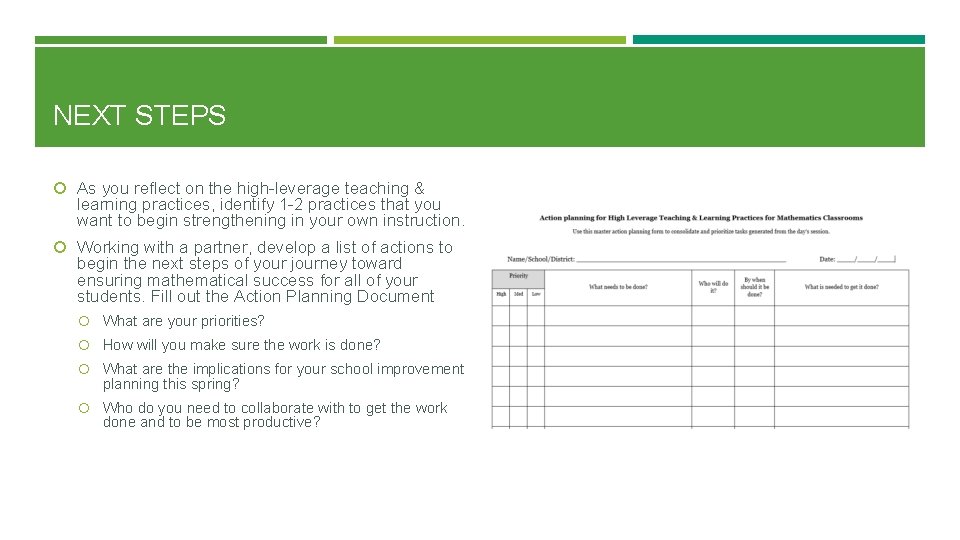
NEXT STEPS As you reflect on the high-leverage teaching & learning practices, identify 1 -2 practices that you want to begin strengthening in your own instruction. Working with a partner, develop a list of actions to begin the next steps of your journey toward ensuring mathematical success for all of your students. Fill out the Action Planning Document What are your priorities? How will you make sure the work is done? What are the implications for your school improvement planning this spring? Who do you need to collaborate with to get the work done and to be most productive?

REFLECTION & FEEDBACK 3: Three things you can ‘get onboard with’ or are excited about the high-leverage teaching & learning practices 2: Two questions you have about the high-leverage teaching & learning practices 1: One critical ‘next-step’ you plan to take moving forward in implementing the high-leverage teaching and learning practices, and when Please complete the conference survey at: http: //bit. ly/innovations 3 H

SUPPORTS AND REFERENCES Achieve the Core, Introduction to the Math Shifts. http: //achievethecore. org/page/399/introduction-to-the- shifts-pd-module and corresponding sample problems http: //achievethecore. org/content/upload/Deep%20 Dive%20 Math%20 PD%20%20 Rigor%20 Activity%20 Sample%20 Problems. pdf NCTM. (2000). Principles and standards for school mathematics. Reston, VA NCTM. (2014). Principles to Actions: Ensuring Mathematical Success for All. Reston, VA Instructional Toolkit for Mathematics, Oakland Unified School District; Leadership, Curriculum and Instruction https: //www. dropbox. com/s/cf 7 w 2 o 9 imvkls 93/OUSDMath. Instructional. Toolkit 201314. pdf? dl=0 Teaching Works, University of Michigan http: //www. teachingworks. org/work-of-teaching/high-leverage- practices

“If we use talk to establish a supportive learning environment, but we do not succeed in creating productive talk about the actual content of mathematics, our students are not likely to succeed in learning the mathematics we want them to know. On the other hand, if we fail to build a supportive learning environment—one in which students can talk about their mathematical thinking without fear of ridicule— then many students will not participate at all. ” —Chapin, O’Connor, and Anderson (2009)