High Dynamic Range from Multiple Images Which Exposures

High Dynamic Range from Multiple Images: Which Exposures to Combine? Michael Grossberg and Shree Nayar CAVE Lab, Columbia University ICCV Workshop on CPMCV October, 2003, Nice, France Partially funded by NSF ITR Award, DARPA/ONR MURI

Low Dynamic Range Exposures Combining Different Exposures + Combination Yields High Dynamic Range [Ginosar and Zeevi, 88, Madden, 93, Mann and Picard, 95, Debevec and Malik, 97, Mitsunaga and Nayar, 99]

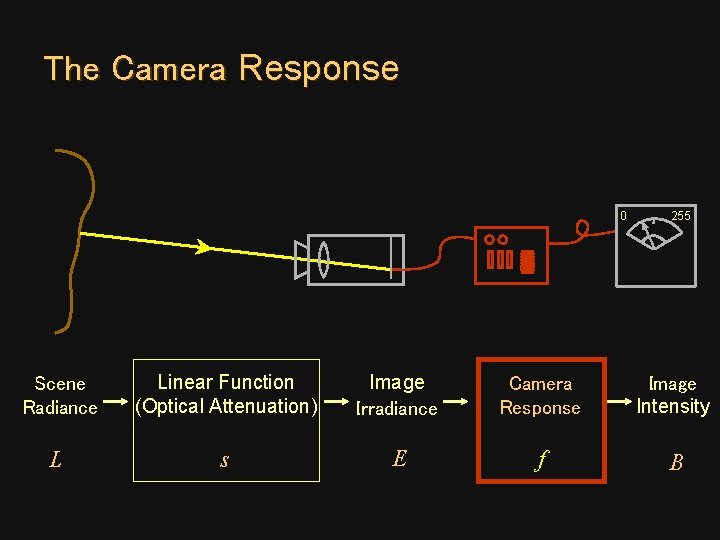
The Camera Response 0 255 Scene Radiance Linear Function (Optical Attenuation) Image Irradiance Camera Response Image Intensity L s E f B

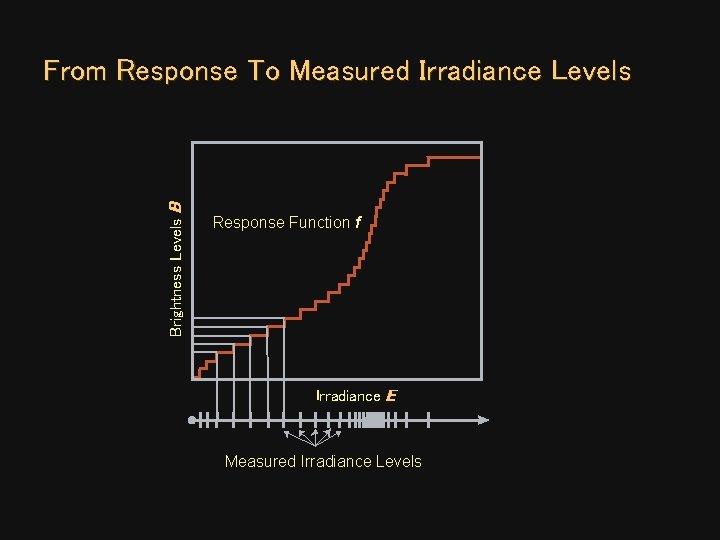
Brightness Levels B From Response To Measured Irradiance Levels Response Function f Irradiance E Measured Irradiance Levels

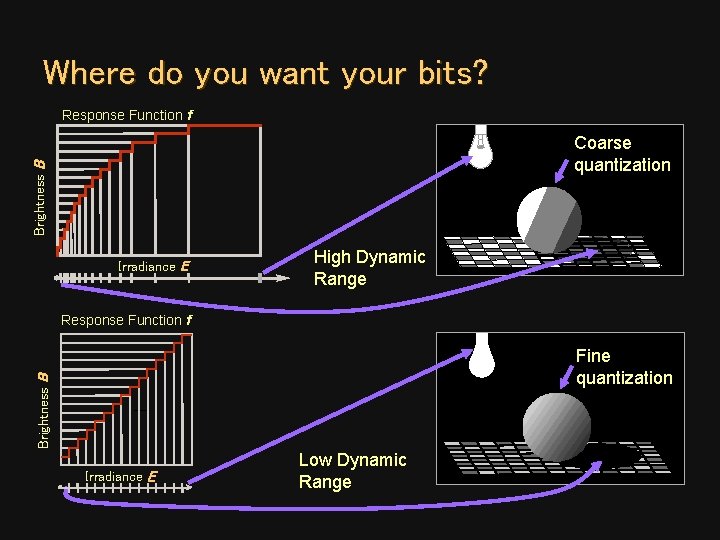
Where do you want your bits? Response Function f Brightness B Coarse quantization Irradiance E High Dynamic Range Response Function f Brightness B Fine quantization Irradiance E Low Dynamic Range

Effective Camera from Multiple Exposures Goal Acquired Images Image from Effective Camera Capture High Dynamic Range + Capture Irradiance Uniformly +

Flexible Dynamic Range Imaging: • Can we create an effective camera with a desired response? – How many exposures are needed? – Which exposures to acquire? – How to combine the acquired images?

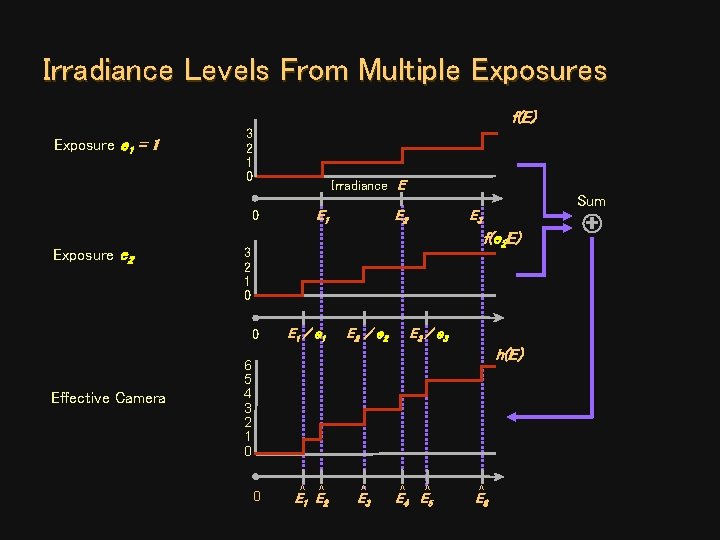
Irradiance Levels From Multiple Exposures f(E) Exposure e 1 = 1 3 2 1 0 Irradiance E E 1 0 Exposure e 2 Sum E 3 f(e 2 E) 3 2 1 0 0 Effective Camera E 2 E 1 / e 1 E 2 / e 2 E 3 / e 3 h(E) 6 5 4 3 2 1 0 0 ^ ^ E 1 E 2 ^ E 3 ^ ^ E 4 E 5 ^ E 6

Response of the Effective Camera Effective Response Number of exposures Exposures Camera Response Irradiance Theorem: The sum of a set of images of a scene taken at different exposures includes all the information in the individual exposures.

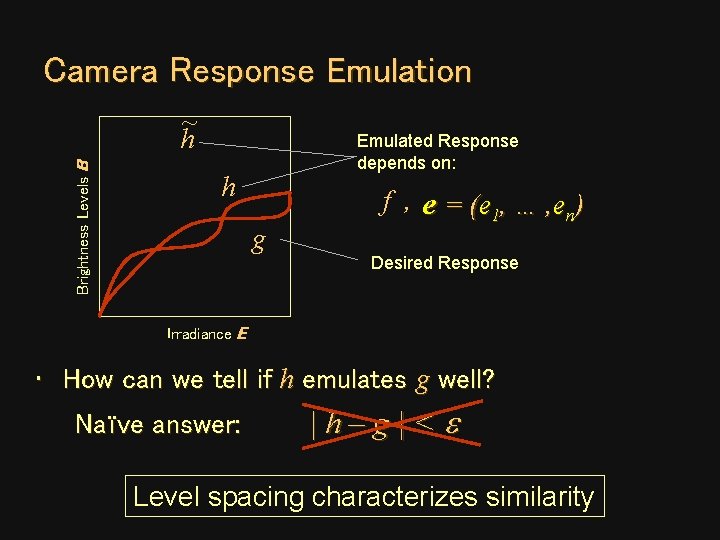
Camera Response Emulation Brightness Levels B ~ h Emulated Response depends on: h g f , e = (e 1, … , en) Desired Response Irradiance E • How can we tell if h emulates g well? Naïve answer: |h–g|<e Level spacing characterizes similarity

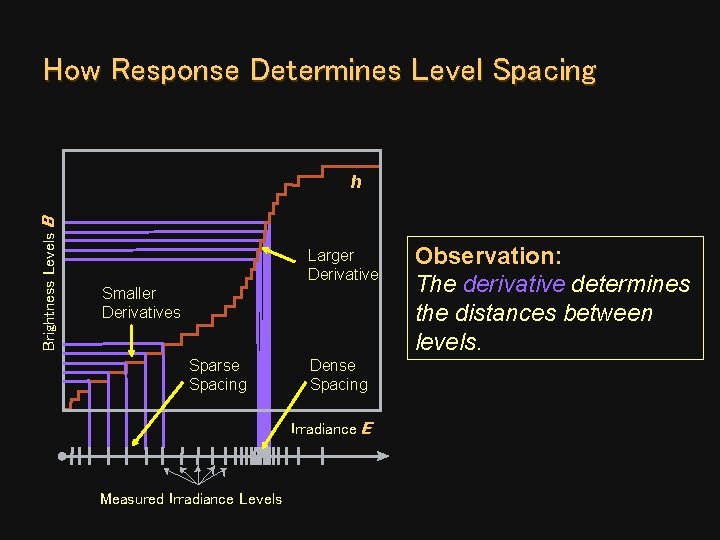
How Response Determines Level Spacing Brightness Levels B h Larger Derivative Smaller Derivatives Sparse Spacing Dense Spacing Irradiance E Measured Irradiance Levels Observation: The derivative determines the distances between levels.

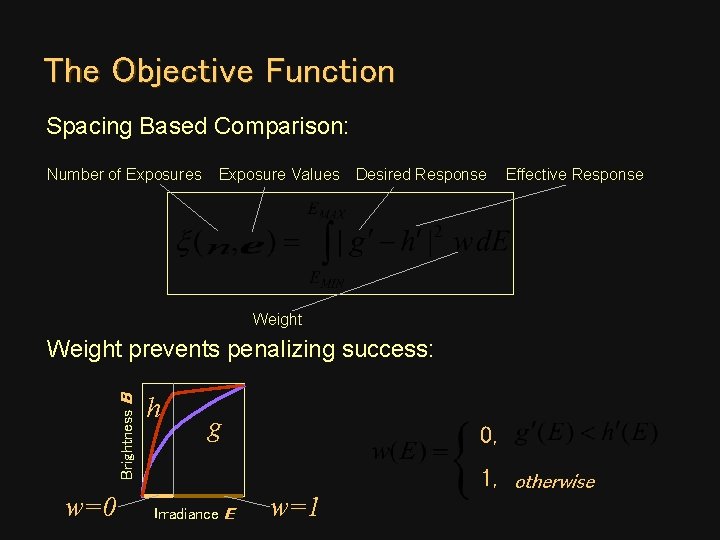
The Objective Function Spacing Based Comparison: Number of Exposures Exposure Values Desired Response Effective Response Weight Brightness B Weight prevents penalizing success: w=0 h g Irradiance E 0, w=1 1, otherwise

Which Exposures and How Many? • For fixed n, find minimizing exposure values e • Choose min n such that error within tolerance • Method: Exhaustive search – Objective function not continuous – Only need to search actual settings – Offline build table of exposures

Flexible Dynamic Range Imaging Effective Camera Linear Gamma = 1/2 Constant contrast (log) Number of Exposures 2 3 4 5 6 1 1 1 1 2 1. 003 1. 015 1. 003 3. 094 1. 003 20. 24 9. 91 4. 689 4. 831 3. 979 Exposure Values 3 4 5 6 2. 985 1. 019 3. 672 1. 007 1. 166 4. 975 1. 007 1. 031 1. 078 5. 636 5. 146 3. 019 11. 23 1. 006 5. 049 18. 56 1. 006 2. 866 8. 564 33. 7 88. 38 37. 23 280 29. 18 144. 9 763. 5 16. 01 64. 22 305. 4 1130

Flexible Dynamic Range Imaging Effective Camera Linear Gamma = 1/2 Constant contrast (log) Number of Exposures 2 3 4 5 6 1 1 1 1 2 1. 003 1. 015 1. 003 3. 094 1. 003 20. 24 9. 91 4. 689 4. 831 3. 979 Exposure Values 3 4 5 6 2. 985 1. 019 1. 007 3. 672 1. 166 1. 031 4. 975 1. 078 5. 636 5. 146 3. 019 1. 006 11. 23 5. 049 2. 866 18. 564 33. 7 88. 38 37. 23 29. 18 16. 01 280 144. 9 64. 22 763. 5 305. 4 1130 Desired Response Constant Contrast Linear Gamma 1/2 Dynamic Range High 1: 16, 000 Medium 1: 1, 000 Low 1: 256

Baseline Exposure Values • Typically exposures are doubled [Ginosar and Zeevi, 88, Madden, 93, Mann and Picard, 95, Debevec and Malik, 97, Mitsunaga and Nayar, 99] • Baseline: Combine the exposures e =(1, 2, 4)

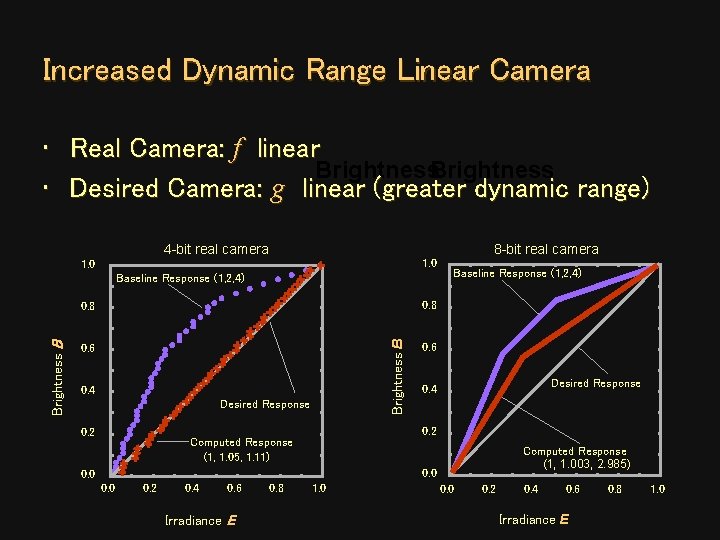
Increased Dynamic Range Linear Camera • Real Camera: f linear Brightness • Desired Camera: g linear (greater dynamic range) 4 -bit real camera 1. 0 Baseline Response (1, 2, 4) 0. 8 Brightness B 8 -bit real camera 0. 6 0. 4 Desired Response 0. 2 0. 6 Desired Response 0. 4 0. 2 Computed Response (1, 1. 05, 1. 11) Computed Response (1, 1. 003, 2. 985) 0. 0 0. 2 0. 4 0. 6 Irradiance E 0. 8 1. 0

Linear Camera: Synthetic Ramp Image High Dynamic Range Linear Camera From baseline exposures (1, 2, 4) From computed exposures (1, 1. 05, 1. 11)

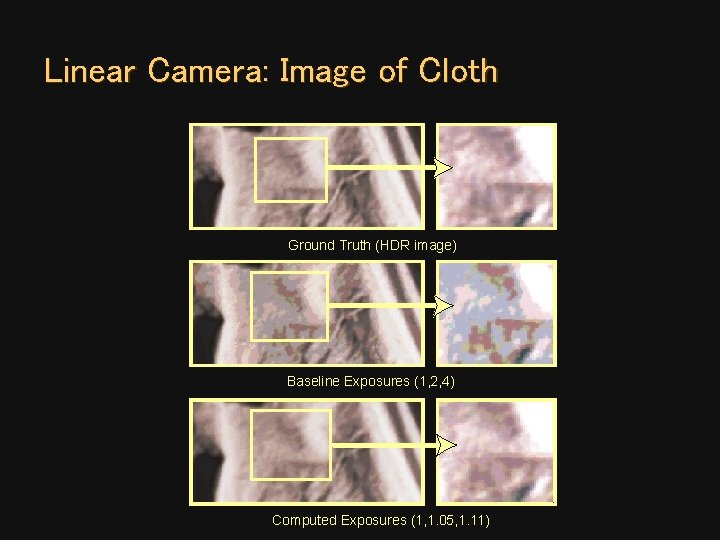
Linear Camera: Image of Cloth Ground Truth (HDR image) Baseline Exposures (1, 2, 4) Computed Exposures (1, 1. 05, 1. 11)

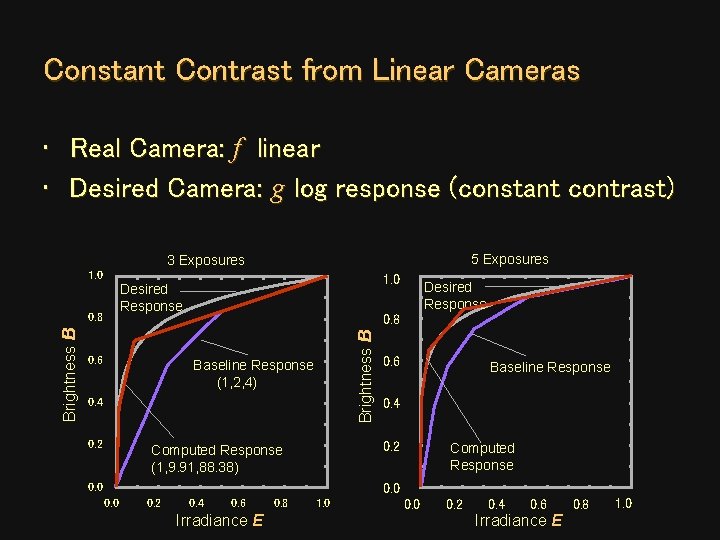
Constant Contrast from Linear Cameras • Real Camera: f linear • Desired Camera: g log response (constant contrast) 5 Exposures 3 Exposures 1. 0 0. 6 Baseline Response (1, 2, 4) 0. 4 0. 2 Desired Response 0. 8 Brightness B 1. 0 Desired Response 0. 6 Baseline Response 0. 4 0. 2 Computed Response (1, 9. 91, 88. 38) 0. 0 Computed Response 0. 0 0. 2 0. 4 0. 6 Irradiance E 0. 8 1. 0

Constant Contrast : Image of Tiles Baseline Exposures Computed Exposures

Linear Camera from Non-linear Camera • Real Camera: f non-linear (Nikon 990) • Desired Camera: g linear Baseline Input Exposures Brightness Combined Iso-brightness Computed Input Exposures Brightness Combined Iso-brightness

Summary • Combine images using summation • Method finds number of exposures and exposure values to use • Emulation of a variety of cameras: Flexible Dynamic Range Imaging