High Dimensional Frequencybin Photonic Entanglement Andrew M Weiner

High Dimensional Frequency-bin Photonic Entanglement Andrew M. Weiner Purdue University June 25, 2020 PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY

Outline • Introduction to frequency bin entanglement • Frequency bin entangled states: how to measure them? • Discrete frequency quantum walks Correlated quantum walk • Picosecond-scale delay metrology PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY

Quantum Light: Why Encoding & Entanglement in Optical Frequency? • Frequencies are robust and compatible with transmission over fibers, but only recently becoming popular for quantum* • Potential for high dimensionality – i. e, qudits – more information per photon • Ability to perform routing based on optical frequency • Manipulation in parallel in frequency domain • Chip-scale microresonator sources • Naturally generate high dimensional photon entanglement in a single-spatial mode • Compatible with photonic integration • Prospects for hyper-entanglement (e. g. , frequency and time, frequency and polarization) Recent reviews: Kues, Reimer, Lukens, Munro, Weiner, Moss, and Morandotti, Nature Photonics 13, 170 (2019); PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY Lu, Weiner, Lougovski, and Lukens, IEEE PTL 31, 1858 (2019)

Acknowledgements Graduated students Poolad Imany Jose Jaramillo Ogaga Odele Poolad Current students Mohammed Al alshaykh Peach Navin Lingaraju Hsuan-Ho (Peach) Lu Alex Moore Suparna Seshadri Faculty and staff Prof. Sabre Kais Dr. Dan Leaird Prof. Minghao Qi Dr. Yi Xuan Ogaga Jose Oak Ridge National Lab Pavel Lougovski Joseph Lukens Nick Peters … Army Research Lab Misha Brodsky Suparna Navin Mohammed Nick Peters Minghao Qi Dan Leaird Sponsors Pavel Lougovski Joe Lukens PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY

Time-Frequency Entangled Photons (Biphotons) Spontaneous parametric down-conversion (SPDC) • Broadband, continuous spectrum (>5 THz) Spontaneous four-wave mixing (SFWM), in a microresonator Frequency correlations Time correlations • Biphoton frequency comb • May be broadband, but made of narrow (discrete) frequency modes • High dimensionality • Frequency bin entanglement: analogies to classical WDM? PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY

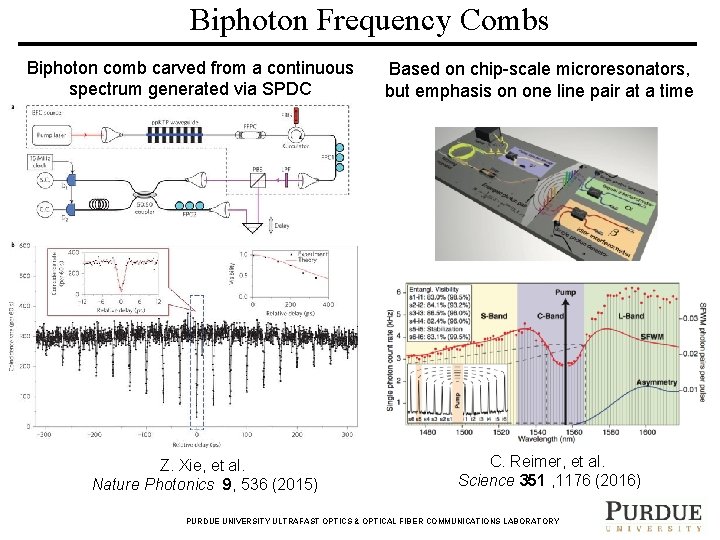
Biphoton Frequency Combs Biphoton comb carved from a continuous spectrum generated via SPDC Z. Xie, et al. Nature Photonics 9, 536 (2015) Based on chip-scale microresonators, but emphasis on one line pair at a time C. Reimer, et al. Science 351 , 1176 (2016) PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY

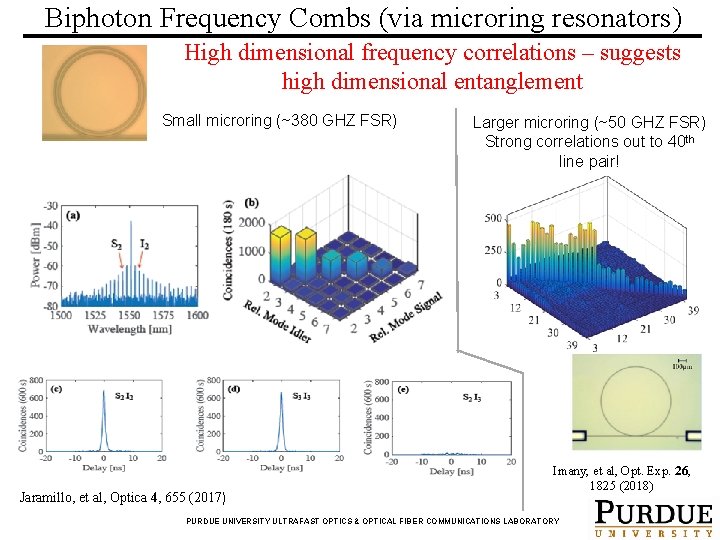
Biphoton Frequency Combs (via microring resonators) High dimensional frequency correlations – suggests high dimensional entanglement Small microring (~380 GHZ FSR) Jaramillo, et al, Optica 4, 655 (2017) Larger microring (~50 GHZ FSR) Strong correlations out to 40 th line pair! Imany, et al, Opt. Exp. 26, 1825 (2018) PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY

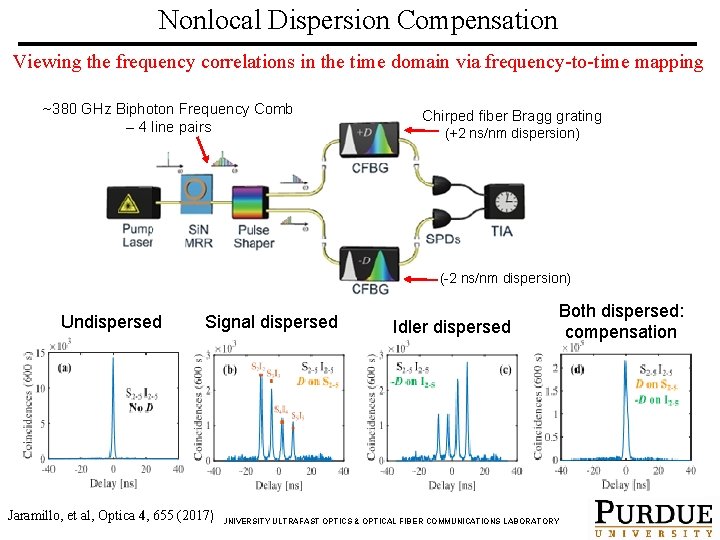
Nonlocal Dispersion Compensation Viewing the frequency correlations in the time domain via frequency-to-time mapping ~380 GHz Biphoton Frequency Comb – 4 line pairs Chirped fiber Bragg grating (+2 ns/nm dispersion) (-2 ns/nm dispersion) Undispersed Signal dispersed Idler dispersed Both dispersed: compensation Jaramillo, et al, Optica 4, 655 (2017) PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY

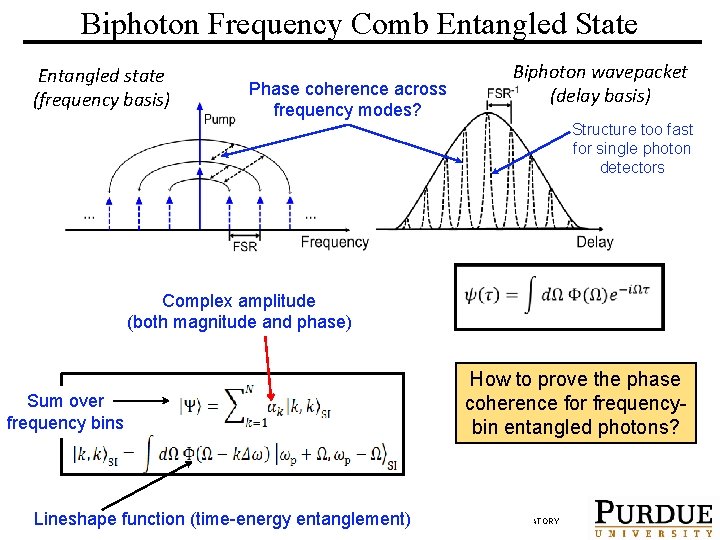
Biphoton Frequency Comb Entangled State Entangled state (frequency basis) Phase coherence across frequency modes? Biphoton wavepacket (delay basis) Structure too fast for single photon detectors Complex amplitude (both magnitude and phase) Sum over frequency bins How to prove the phase coherence for frequencybin entangled photons? UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY Lineshape function PURDUE (time-energy entanglement)

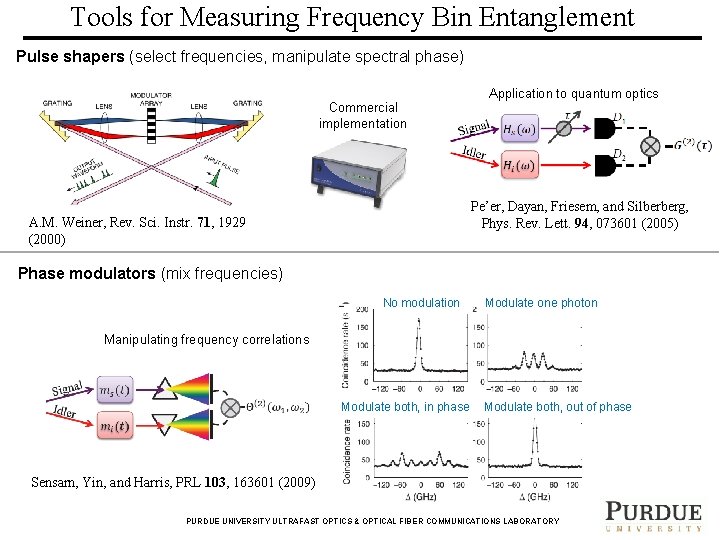
Tools for Measuring Frequency Bin Entanglement Pulse shapers (select frequencies, manipulate spectral phase) Commercial implementation Application to quantum optics Pe’er, Dayan, Friesem, and Silberberg, Phys. Rev. Lett. 94, 073601 (2005) A. M. Weiner, Rev. Sci. Instr. 71, 1929 (2000) Phase modulators (mix frequencies) No modulation Modulate one photon Manipulating frequency correlations Modulate both, in phase Modulate both, out of phase Sensarn, Yin, and Harris, PRL 103, 163601 (2009) PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY

[Classical] Pulse Shaping via Spectral Phase Control Linear phase A>0 Quadratic phase A=0 A<0 • Programmable delay chirp compensated chirped • Linear chirp Weiner et al, IEEE J. Quant. Electron. 28, 908 (1992) Cubic phase • Nonlinear chirp Efimov et al, J. Opt. Soc. Am. B 12, 1968 (1995) PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY

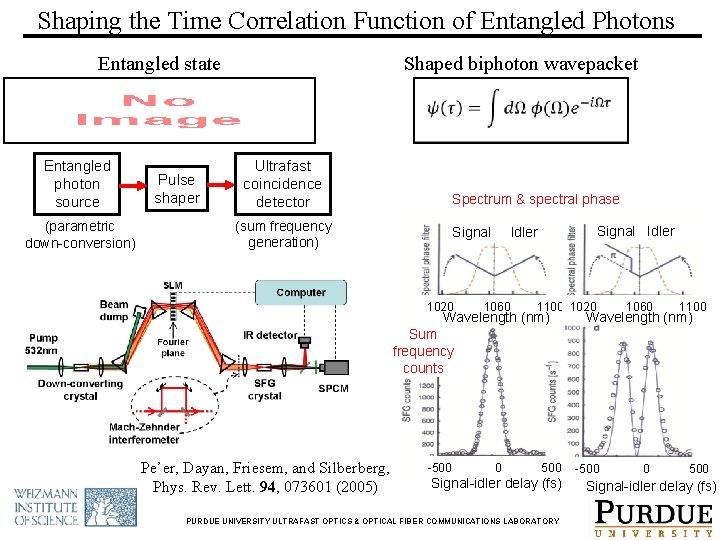
Shaping the Time Correlation Function of Entangled Photons Entangled state Entangled photon source (parametric down-conversion) Pulse shaper Shaped biphoton wavepacket Ultrafast coincidence detector Spectrum & spectral phase (sum frequency generation) Signal 1020 Signal Idler 1060 1100 1020 Wavelength (nm) 1060 1100 Wavelength (nm) Sum frequency counts Pe’er, Dayan, Friesem, and Silberberg, Phys. Rev. Lett. 94, 073601 (2005) -500 0 500 Signal-idler delay (fs) PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY -500 0 500 Signal-idler delay (fs)

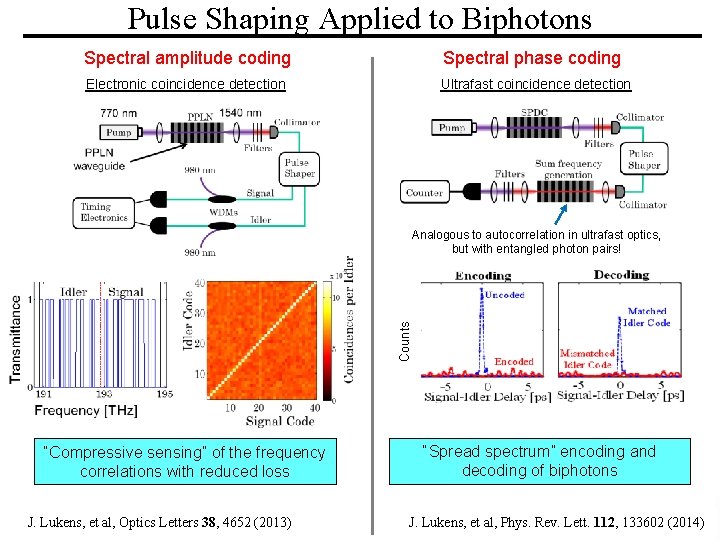
Pulse Shaping Applied to Biphotons Spectral amplitude coding Spectral phase coding Electronic coincidence detection Ultrafast coincidence detection Counts Analogous to autocorrelation in ultrafast optics, but with entangled photon pairs! “Compressive sensing” of the frequency correlations with reduced loss “Spread spectrum” encoding and decoding of biphotons PURDUE ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY J. Lukens, et al, Phys. Rev. Lett. 112, 133602 (2014) J. Lukens, et al, Optics Letters 38, UNIVERSITY 4652 (2013)

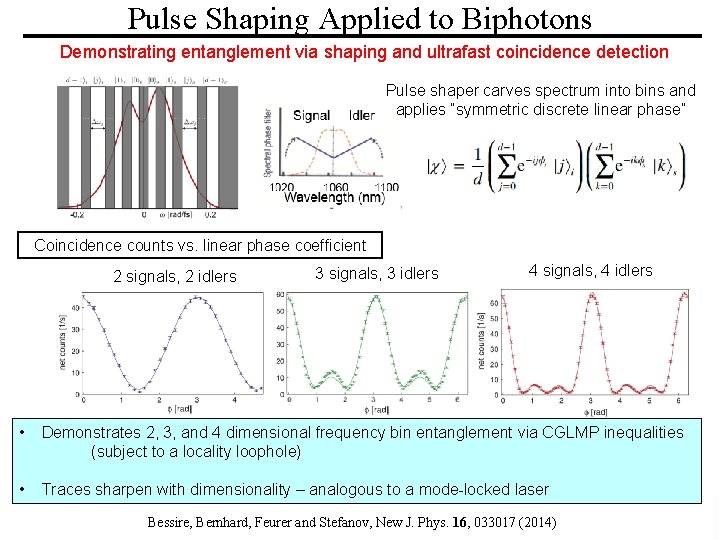
Pulse Shaping Applied to Biphotons Demonstrating entanglement via shaping and ultrafast coincidence detection Pulse shaper carves spectrum into bins and applies “symmetric discrete linear phase” Coincidence counts vs. linear phase coefficient 2 signals, 2 idlers 3 signals, 3 idlers 4 signals, 4 idlers • Demonstrates 2, 3, and 4 dimensional frequency bin entanglement via CGLMP inequalities (subject to a locality loophole) • Traces sharpen with dimensionality – analogous to a mode-locked laser UNIVERSITY ULTRAFAST OPTICS & OPTICAL COMMUNICATIONS LABORATORY Bessire, PURDUE Bernhard, Feurer and Stefanov, New. FIBER J. Phys. 16, 033017 (2014)

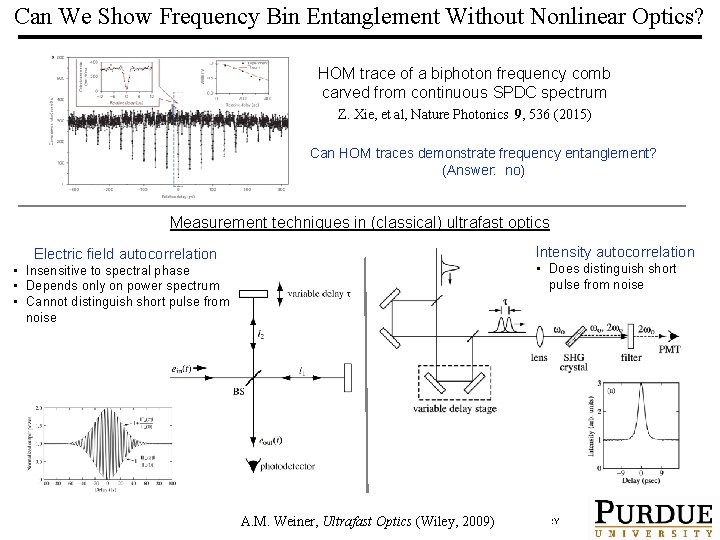
Can We Show Frequency Bin Entanglement Without Nonlinear Optics? HOM trace of a biphoton frequency comb carved from continuous SPDC spectrum Z. Xie, et al, Nature Photonics 9, 536 (2015) Can HOM traces demonstrate frequency entanglement? (Answer: no) Measurement techniques in (classical) ultrafast optics Intensity autocorrelation Electric field autocorrelation • Does distinguish short pulse from noise • Insensitive to spectral phase • Depends only on power spectrum • Cannot distinguish short pulse from noise A. M. Weiner, Ultrafast Optics (Wiley, 2009) PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY

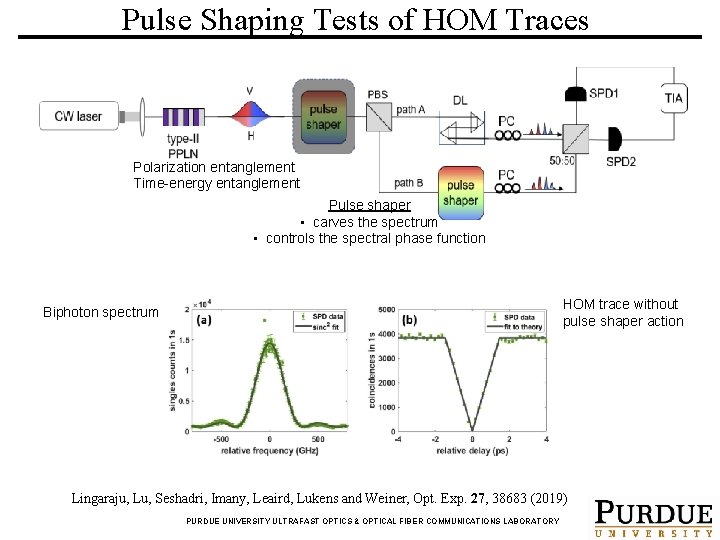
Pulse Shaping Tests of HOM Traces Polarization entanglement Time-energy entanglement Pulse shaper • carves the spectrum • controls the spectral phase function HOM trace without pulse shaper action Biphoton spectrum Lingaraju, Lu, Seshadri, Imany, Leaird, Lukens and Weiner, Opt. Exp. 27, 38683 (2019) PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY

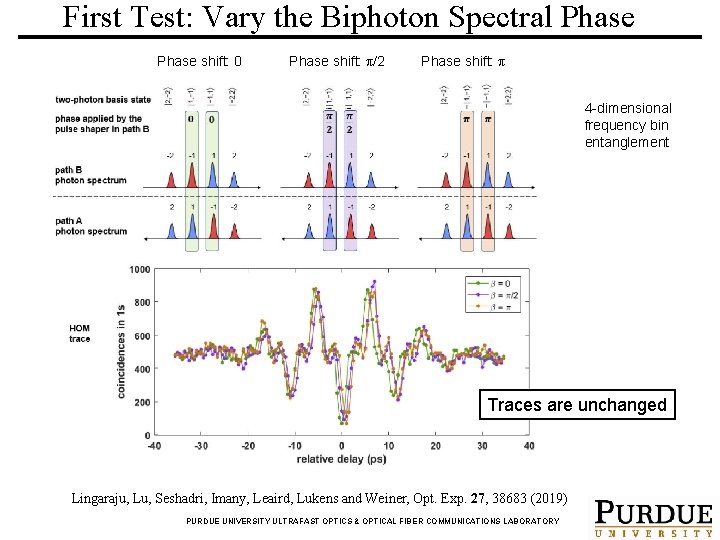
First Test: Vary the Biphoton Spectral Phase shift: 0 Phase shift: π/2 Phase shift: π 4 -dimensional frequency bin entanglement Traces are unchanged Lingaraju, Lu, Seshadri, Imany, Leaird, Lukens and Weiner, Opt. Exp. 27, 38683 (2019) PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY

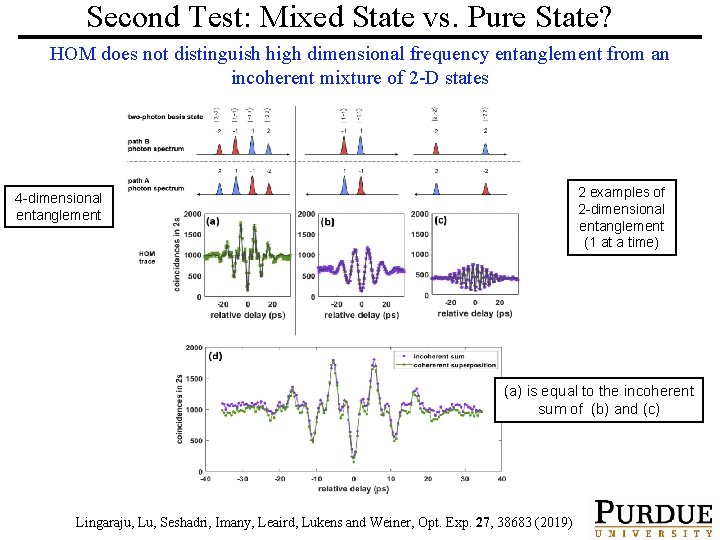
Second Test: Mixed State vs. Pure State? HOM does not distinguish high dimensional frequency entanglement from an incoherent mixture of 2 -D states 2 examples of 2 -dimensional entanglement (1 at a time) 4 -dimensional entanglement (a) is equal to the incoherent sum of (b) and (c) PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY Lingaraju, Lu, Seshadri, Imany, Leaird, Lukens and Weiner, Opt. Exp. 27, 38683 (2019)

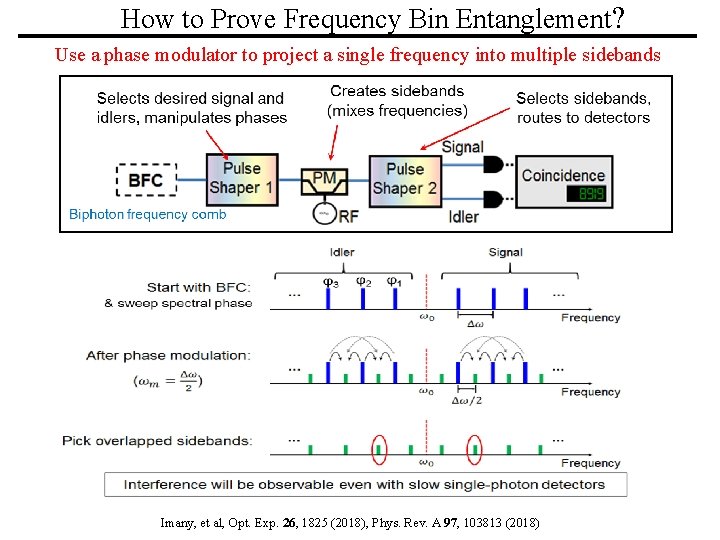
How to Prove Frequency Bin Entanglement? Use a phase modulator to project a single frequency into multiple sidebands PURDUE ULTRAFAST & OPTICAL Imany, et al, UNIVERSITY Opt. Exp. 26, 1825 OPTICS (2018), Phys. FIBER Rev. COMMUNICATIONS A 97, 103813 LABORATORY (2018)

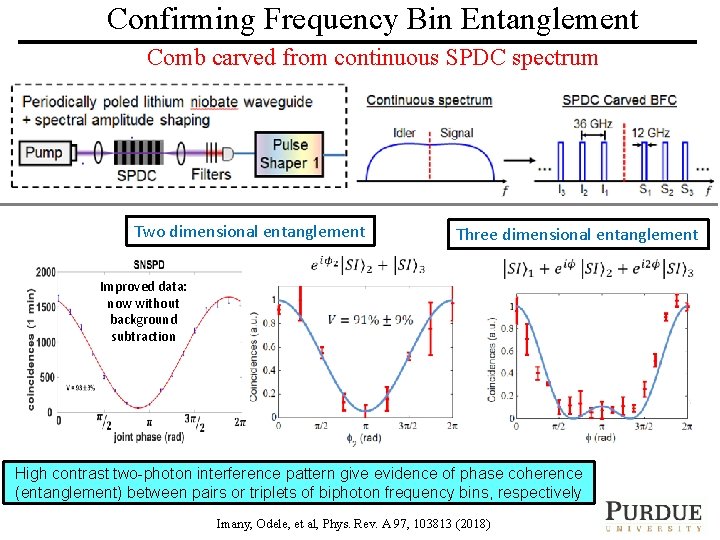
Confirming Frequency Bin Entanglement Comb carved from continuous SPDC spectrum Two dimensional entanglement Three dimensional entanglement Improved data: now without background subtraction High contrast two-photon interference pattern give evidence of phase coherence (entanglement) between pairs or triplets of biphoton frequency bins, respectively Imany, Odele, et al, Phys. Rev. A 97, 103813 (2018) PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY

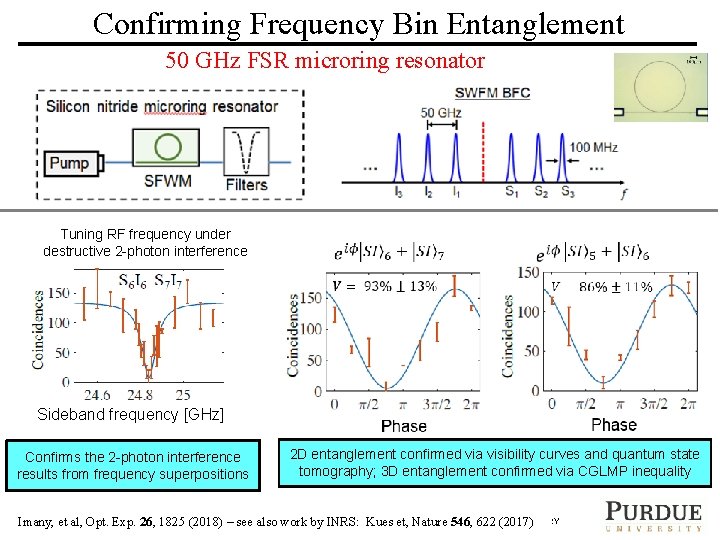
Confirming Frequency Bin Entanglement 50 GHz FSR microring resonator Tuning RF frequency under destructive 2 -photon interference Sideband frequency [GHz] Confirms the 2 -photon interference results from frequency superpositions Phase 2 D entanglement confirmed via visibility curves and quantum state tomography; 3 D entanglement confirmed via CGLMP inequality FIBER COMMUNICATIONS LABORATORY Imany, et al, Opt. Exp. 26, 1825 PURDUE (2018)UNIVERSITY – see also. ULTRAFAST work by. OPTICS INRS: & OPTICAL Kues et, Nature 546, 622 (2017)

Frequency Quantum Walk PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY

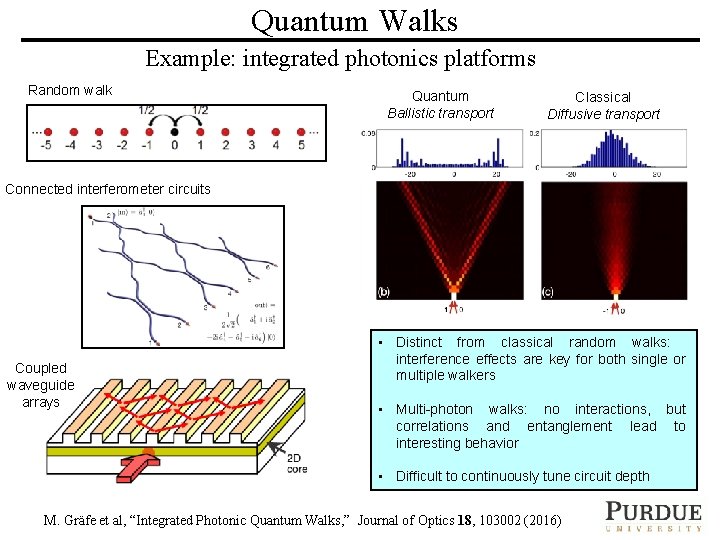
Quantum Walks Example: integrated photonics platforms Random walk Quantum Ballistic transport Classical Diffusive transport Connected interferometer circuits Coupled waveguide arrays • Distinct from classical random walks: interference effects are key for both single or multiple walkers • Multi-photon walks: no interactions, but correlations and entanglement lead to interesting behavior • Difficult to continuously tune circuit depth UNIVERSITY ULTRAFAST OPTICS &Journal OPTICAL FIBER COMMUNICATIONS LABORATORY M. Gräfe et al, “Integrated. PURDUE Photonic Quantum Walks, ” of Optics 18, 103002 (2016)

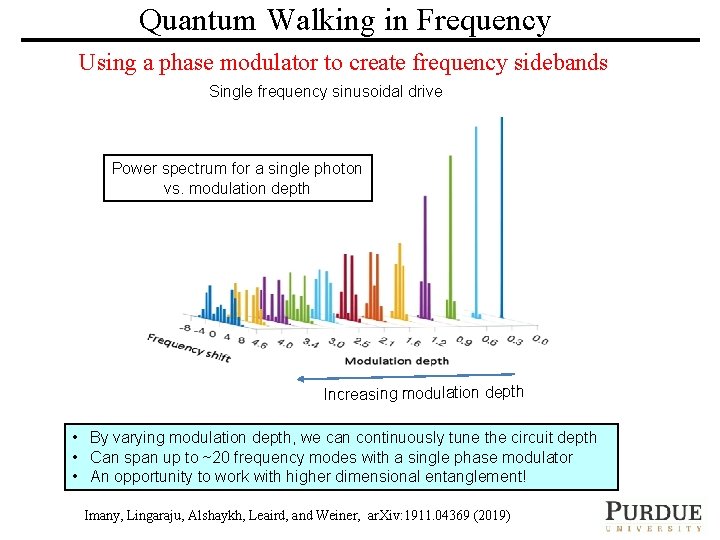
Quantum Walking in Frequency Using a phase modulator to create frequency sidebands Single frequency sinusoidal drive Power spectrum for a single photon vs. modulation depth Increasing modulation depth • By varying modulation depth, we can continuously tune the circuit depth • Can span up to ~20 frequency modes with a single phase modulator • An opportunity to work with higher dimensional entanglement! Imany, Lingaraju, PURDUE Alshaykh, Leaird, and Weiner, ar. Xiv: 1911. 04369 (2019) UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY

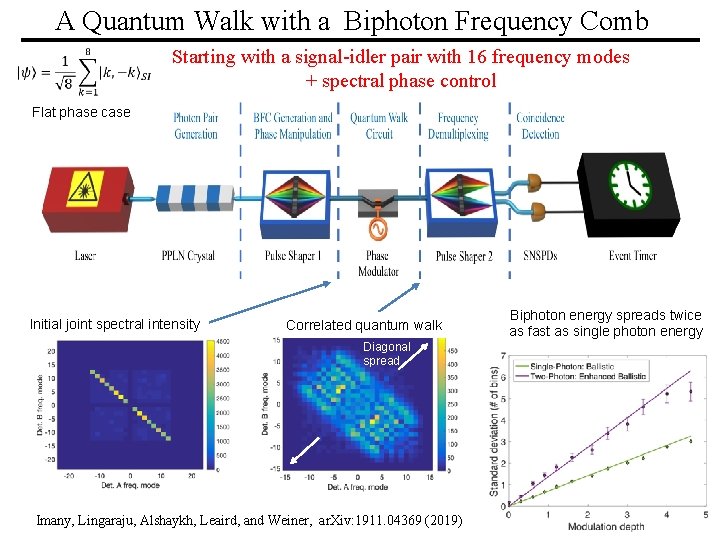
A Quantum Walk with a Biphoton Frequency Comb Starting with a signal-idler pair with 16 frequency modes + spectral phase control Flat phase case Initial joint spectral intensity Correlated quantum walk Biphoton energy spreads twice as fast as single photon energy Diagonal spread PURDUE UNIVERSITY ULTRAFASTar. Xiv: 1911. 04369 OPTICS & OPTICAL FIBER (2019) COMMUNICATIONS LABORATORY Imany, Lingaraju, Alshaykh, Leaird, and Weiner,

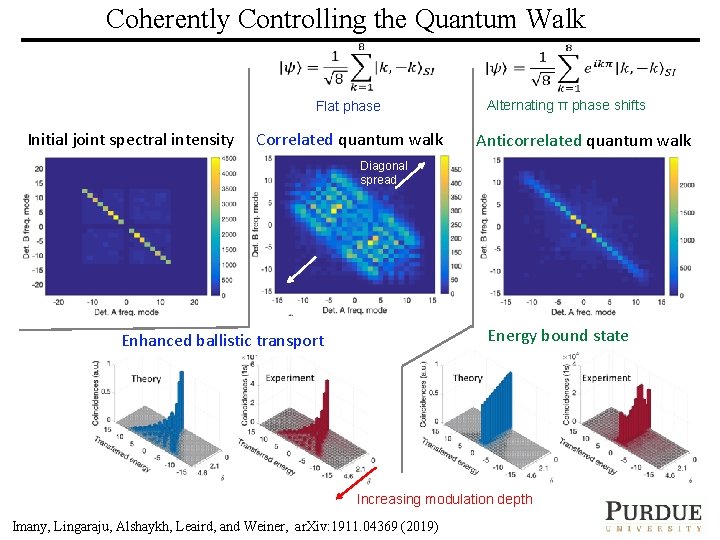
Coherently Controlling the Quantum Walk Flat phase Initial joint spectral intensity Correlated quantum walk Alternating π phase shifts Anticorrelated quantum walk Diagonal spread Enhanced ballistic transport Energy bound state Increasing modulation depth PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY Imany, Lingaraju, Alshaykh, Leaird, and Weiner, ar. Xiv: 1911. 04369 (2019)

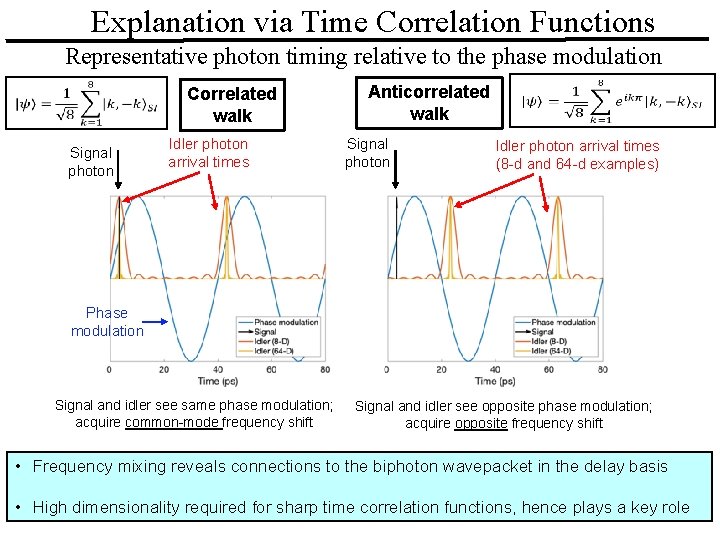
Explanation via Time Correlation Functions Representative photon timing relative to the phase modulation Correlated walk Signal photon Idler photon arrival times Anticorrelated walk Signal photon Idler photon arrival times (8 -d and 64 -d examples) Phase modulation Signal and idler see same phase modulation; acquire common-mode frequency shift Signal and idler see opposite phase modulation; acquire opposite frequency shift • Frequency mixing reveals connections to the biphoton wavepacket in the delay basis • High dimensionality required for sharp time correlation functions, hence plays a key role PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY

Delay Metrology PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY

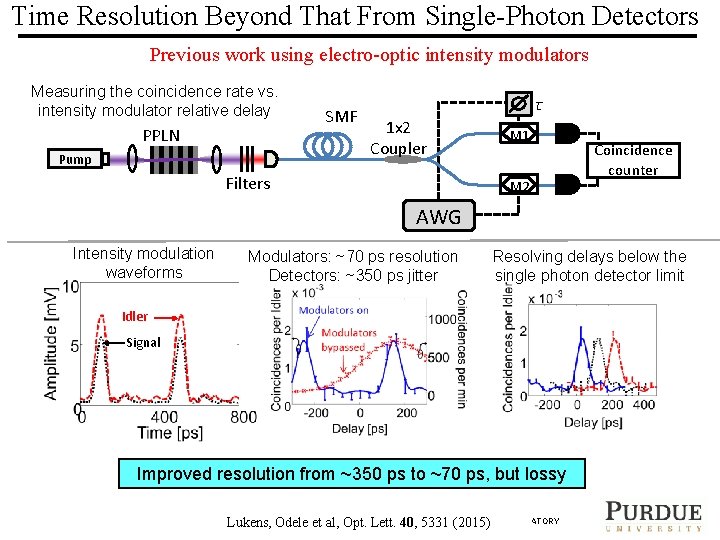
Time Resolution Beyond That From Single-Photon Detectors Previous work using electro-optic intensity modulators Measuring the coincidence rate vs. intensity modulator relative delay PPLN Pump SMF τ 1 x 2 Coupler Filters M 1 M 2 Coincidence counter AWG Intensity modulation waveforms Modulators: ~70 ps resolution Detectors: ~350 ps jitter Resolving delays below the single photon detector limit Idler Signal Improved resolution from ~350 ps to ~70 ps, but lossy Lukens, Odele et al, Opt. Lett. 40, 5331 (2015) PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY

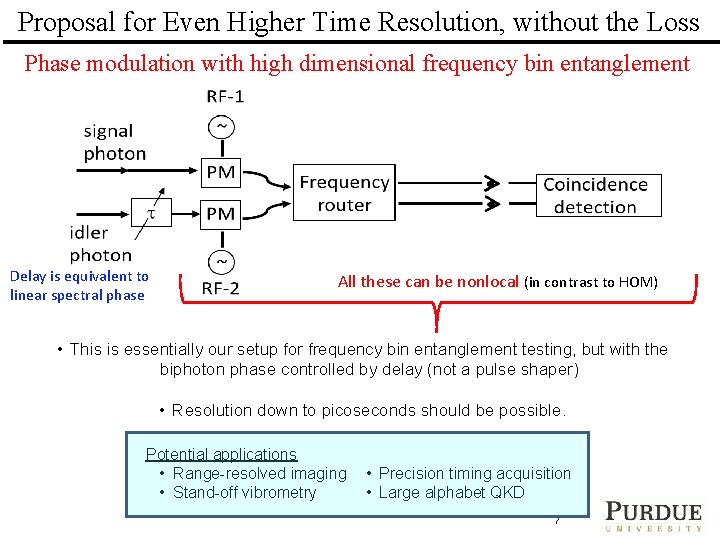
Proposal for Even Higher Time Resolution, without the Loss Phase modulation with high dimensional frequency bin entanglement Delay is equivalent to linear spectral phase All these can be nonlocal (in contrast to HOM) • This is essentially our setup for frequency bin entanglement testing, but with the biphoton phase controlled by delay (not a pulse shaper) • Resolution down to picoseconds should be possible. Potential applications • Range-resolved imaging • Stand-off vibrometry • Precision timing acquisition • Large alphabet QKD PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY

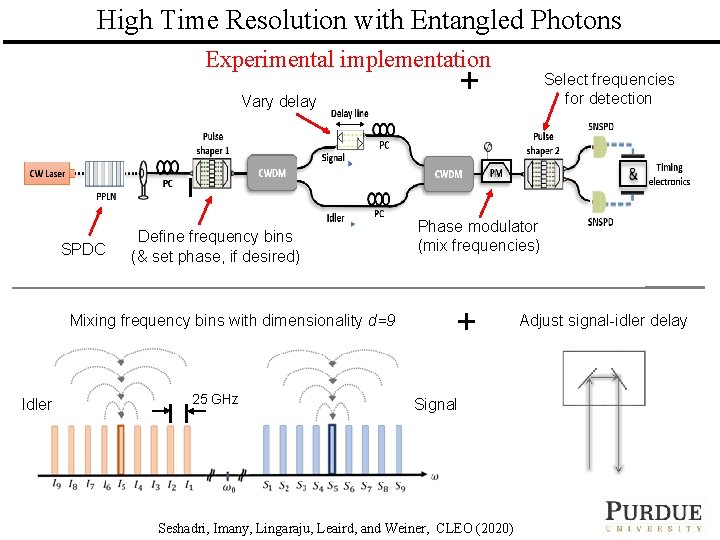
High Time Resolution with Entangled Photons Experimental implementation Vary delay SPDC Define frequency bins (& set phase, if desired) Mixing frequency bins with dimensionality d=9 Idler 25 GHz + Select frequencies for detection Phase modulator (mix frequencies) + Adjust signal-idler delay Signal PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY Seshadri, Imany, Lingaraju, Leaird, and Weiner, CLEO (2020)

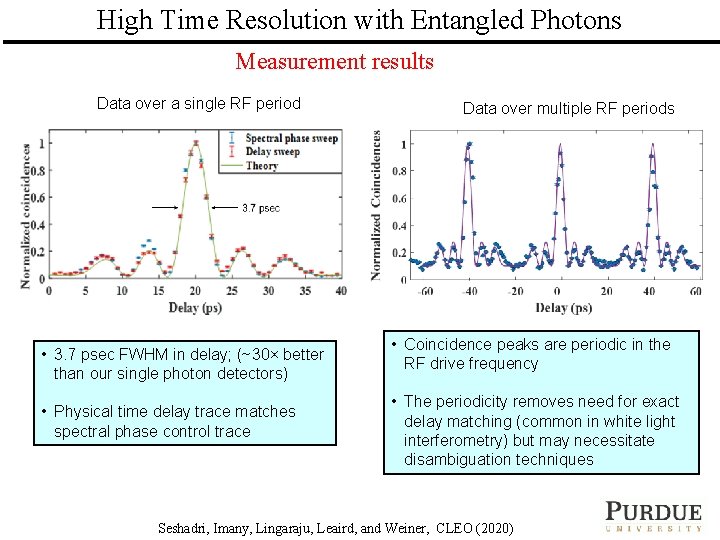
High Time Resolution with Entangled Photons Measurement results Data over a single RF period • 3. 7 psec FWHM in delay; (~30× better than our single photon detectors) • Physical time delay trace matches spectral phase control trace Data over multiple RF periods • Coincidence peaks are periodic in the RF drive frequency • The periodicity removes need for exact delay matching (common in white light interferometry) but may necessitate disambiguation techniques PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY Seshadri, Imany, Lingaraju, Leaird, and Weiner, CLEO (2020)

Thanks to many students, collaborators, & sponsors! • Proving the phase coherence / entanglement for frequency bin photons, including those from on-chip microring resonator sources • Exploring the use of high dimensionality • Coherently controlled discrete frequency quantum walks • Ultrafast delay resolution PURDUE UNIVERSITY ULTRAFAST OPTICS & OPTICAL FIBER COMMUNICATIONS LABORATORY