HIFI NMR part 1 automated backbone assignments using

HIFI NMR : part 1 automated backbone assignments using 3 D->2 D Marco Tonelli National Magnetic Resonance Facility At Madison NMRFAM

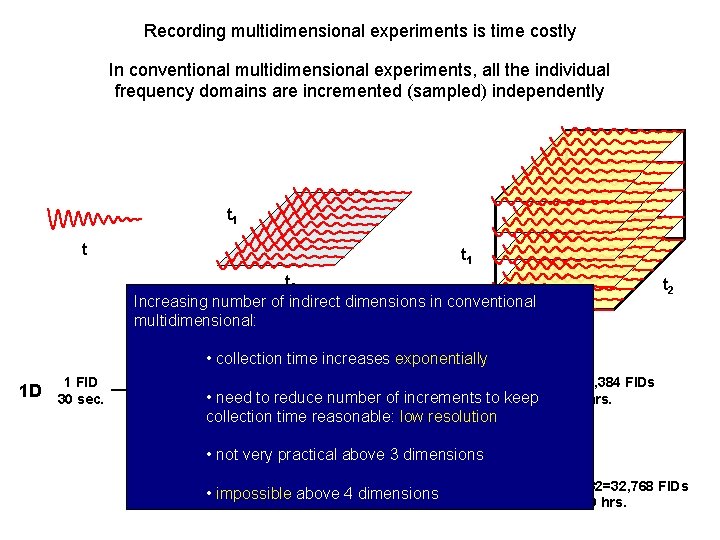
Recording multidimensional experiments is time costly In conventional multidimensional experiments, all the individual frequency domains are incremented (sampled) independently t 1 t 2 Increasing number of indirect dimensions in conventional multidimensional: t 2 t 3 • collection time increases exponentially 1 D 1 FID 30 sec. t : 128 FIDs t x t : 128 x 128=16, 384 FIDs 1 2 1 3 D 2 D to • need reduce number of increments to keep 5 days 16 hrs. 64 min. collection time reasonable: low resolution • not very practical above 3 dimensions • impossible above 4 dimensions 4 D t 1 x t 2 x t 3 : 32 x 32=32, 768 FIDs 11 days 9 hrs.

Fast methods Reduced Sampling Reduced Dimensionality Hadamard spectroscopy single-scan NMR so-fast NMR

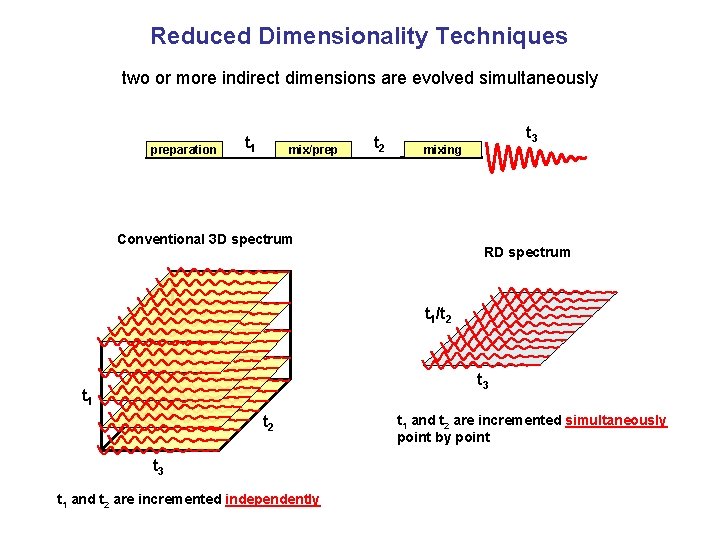
Reduced Dimensionality Techniques two or more indirect dimensions are evolved simultaneously preparation t 1 mix/prep t 2 t 3 mixing Conventional 3 D spectrum RD spectrum t 1/t 2 t 3 t 1 and t 2 are incremented independently t 1 and t 2 are incremented simultaneously point by point

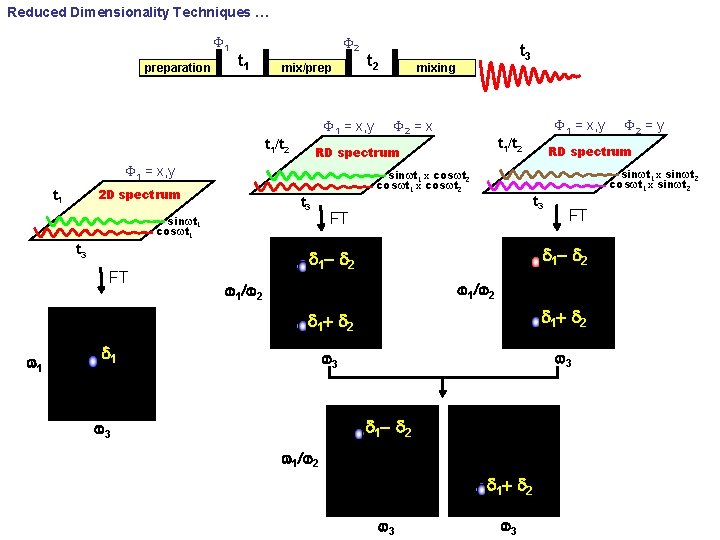
Reduced Dimensionality Techniques … F 1 preparation t 1 F 2 mix/prep t 2 F 1 = x, y t 1/t 2 t 3 sinwt 1 coswt 1 t 3 w 1 F 1 = x, y F 2 = x t 1/t 2 RD spectrum t 3 FT FT d 1 - d 2 w 1/w 2 d 1 + d 2 w 3 d 1 - d 2 w 3 w 1/w 2 d 1 + d 2 w 3 F 2 = y sinwt 1 x sinwt 2 coswt 1 x sinwt 2 sinwt 1 x coswt 2 coswt 1 x coswt 2 2 D spectrum FT mixing RD spectrum F 1 = x, y t 1 t 3 w 3

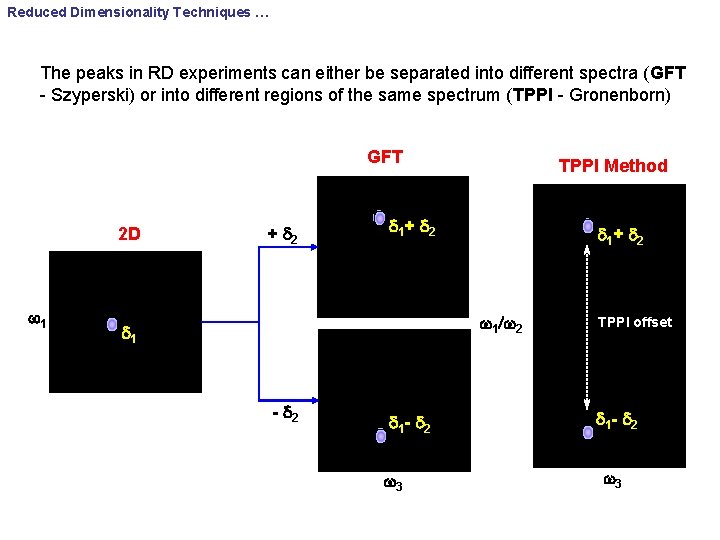
Reduced Dimensionality Techniques … The peaks in RD experiments can either be separated into different spectra (GFT - Szyperski) or into different regions of the same spectrum (TPPI - Gronenborn) GFT 2 D w 1 + d 2 TPPI Method d 1 + d 2 w 1/w 2 d 1 - d 2 w 3 TPPI offset d 1 - d 2 w 3

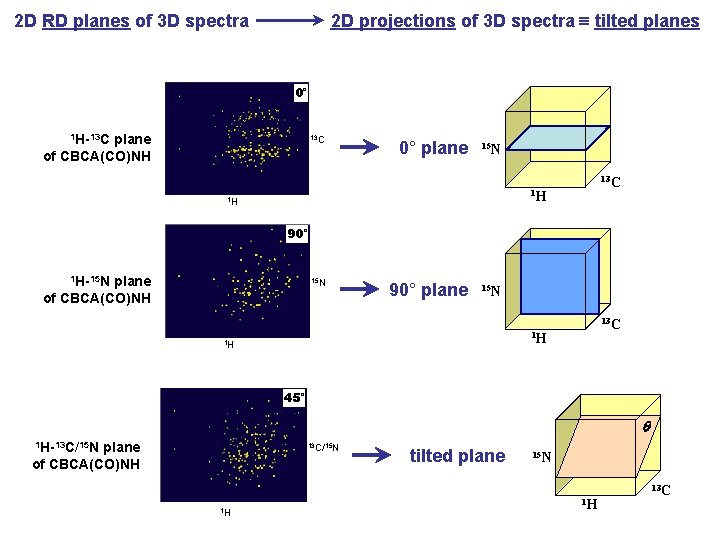
2 D projections of 3 D spectra tilted planes 2 D RD planes of 3 D spectra 0° 1 H-13 C plane of CBCA(CO)NH 13 C 0° plane 15 N 13 C 1 H 1 H 90° 1 H-15 N plane of CBCA(CO)NH 15 N 90° plane 15 N 13 C 1 H 1 H 45° q 1 H-13 C/15 N plane of CBCA(CO)NH 13 C/15 N 1 H tilted plane 15 N 1 H 13 C

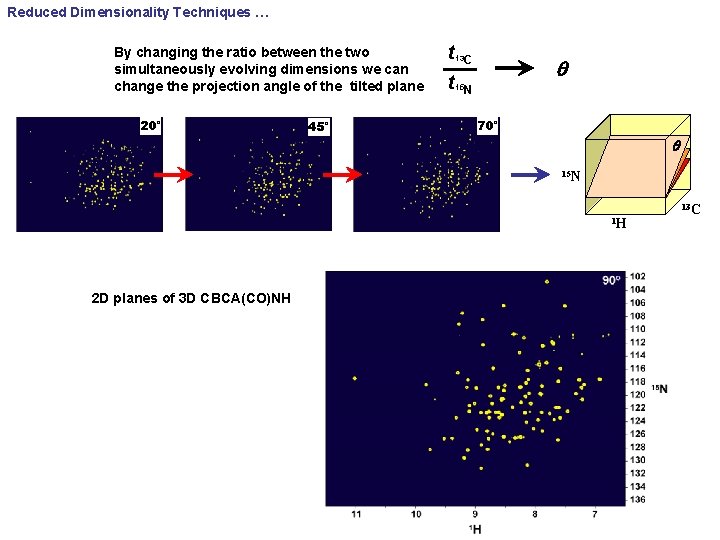
Reduced Dimensionality Techniques … By changing the ratio between the two simultaneously evolving dimensions we can change the projection angle of the tilted plane 20° 45° t t 13 C q 15 N 70° q 15 N 1 H 2 D planes of 3 D CBCA(CO)NH 13 C

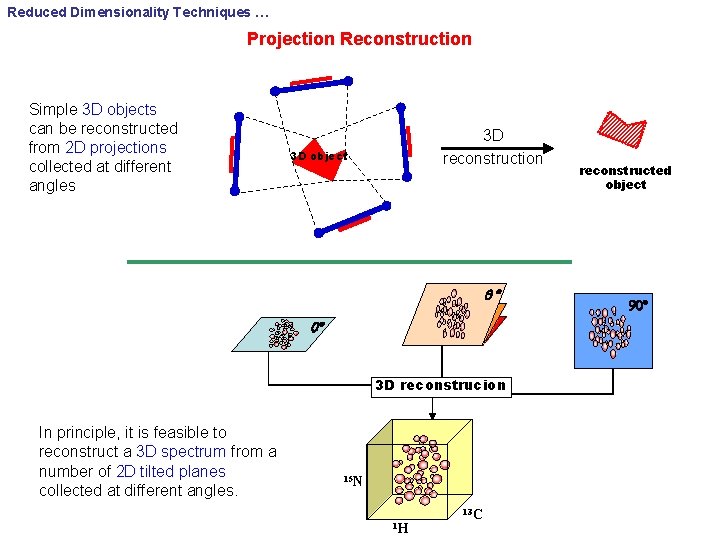
Reduced Dimensionality Techniques … Projection Reconstruction Simple 3 D objects can be reconstructed from 2 D projections collected at different angles 3 D reconstruction 3 D object q 0 3 D reconstrucion In principle, it is feasible to reconstruct a 3 D spectrum from a number of 2 D tilted planes collected at different angles. 15 N 1 H 13 C reconstructed object 90

Reduced Dimensionality Techniques … GFT / TPPI method Projection-Reconstruction n-dimensional experiments are run as two-dimensional RD spectra multiple tilted planes are collected at different angles split peaks can be separated into different spectra (GFT) or different regions of the same spectrum (TPPI) n-dimensional spectra are reconstructed from several tilted planes indirect frequencies are extracted from analysis of split patterns High-resolution Iterative Frequency Identification HIFI simultaneously evolving indirect frequencies are extracted from twodimensional RD spectra multiple tilted planes are used angle of tilted planes is chosen adaptively in real time

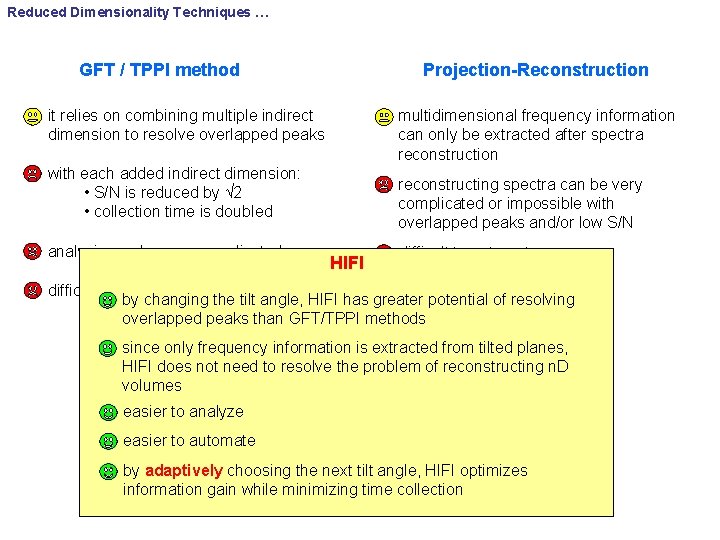
Reduced Dimensionality Techniques … GFT / TPPI method Projection-Reconstruction it relies on combining multiple indirect dimension to resolve overlapped peaks multidimensional frequency information can only be extracted after spectra reconstruction with each added indirect dimension: • S/N is reduced by √ 2 • collection time is doubled analysis can be very complicated reconstructing spectra can be very complicated or impossible with overlapped peaks and/or low S/N HIFI difficult to automate by changing the tilt angle, HIFI has greater potential of resolving overlapped peaks than GFT/TPPI methods since only frequency information is extracted from tilted planes, HIFI does not need to resolve the problem of reconstructing n. D volumes easier to analyze easier to automate by adaptively choosing the next tilt angle, HIFI optimizes information gain while minimizing time collection

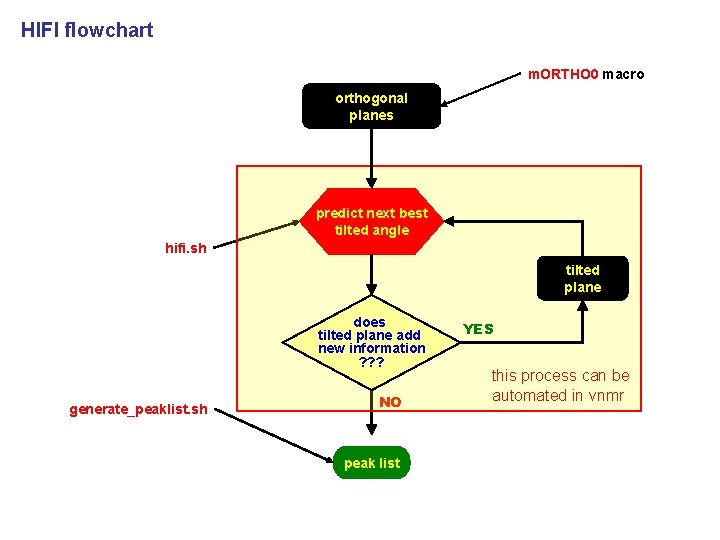
HIFI flowchart m. ORTHO 0 macro orthogonal planes predict next best tilted angle hifi. sh tilted plane does tilted plane add new information ? ? ? generate_peaklist. sh NO peak list YES this process can be automated in vnmr

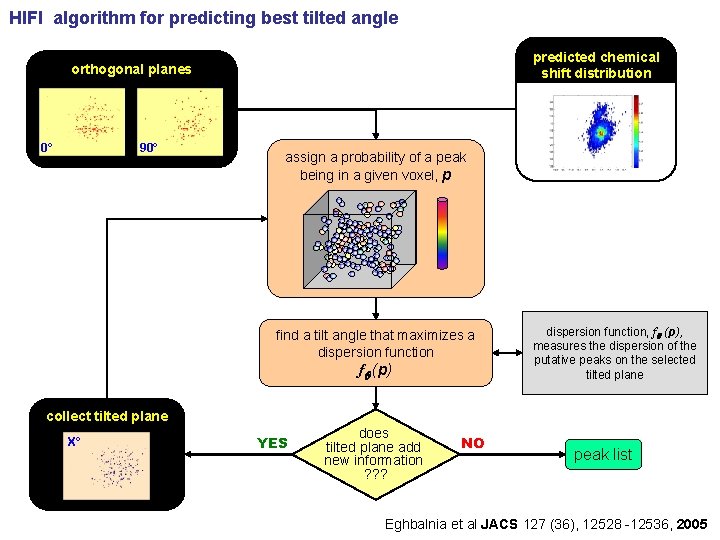
HIFI algorithm for predicting best tilted angle predicted chemical shift distribution orthogonal planes 0° 90° assign a probability of a peak being in a given voxel, p find a tilt angle that maximizes a dispersion function fq (p) dispersion function, fq (p), measures the dispersion of the putative peaks on the selected tilted plane collect tilted plane X° YES does tilted plane add new information ? ? ? NO peak list Eghbalnia et al JACS 127 (36), 12528 -12536, 2005

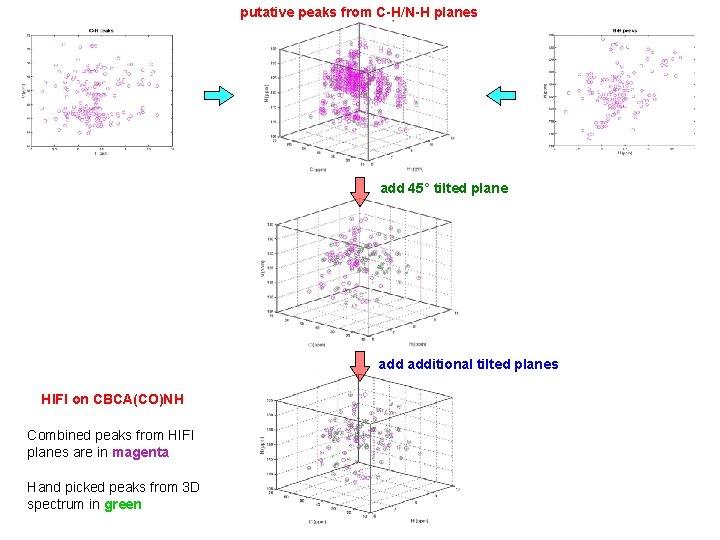
putative peaks from C-H/N-H planes add 45° tilted plane additional tilted planes HIFI on CBCA(CO)NH Combined peaks from HIFI planes are in magenta Hand picked peaks from 3 D spectrum in green

Using HIFI for backbone assignments Modified Bio. Pack experiments for backbone assignments HNCO HN(CO)CA HNCA CBCA(CO)NH HN(CA)CB HNCACB NH sensitivity enhanced TROSY option standard sequences are robust and offer the best S/N for backbone assignments we rely on HIFI ability to adaptively select tilted planes to resolve overlapped peaks added HIFI option for collecting tilted planes 13 C and 15 N indirect dimensions are evolved simultaneously added semi-constant time 15 N evolution to allow collecting tilted planes with more indirect points for higher resolution optimized for cryogenic probes Needs AUTOMATION !!!

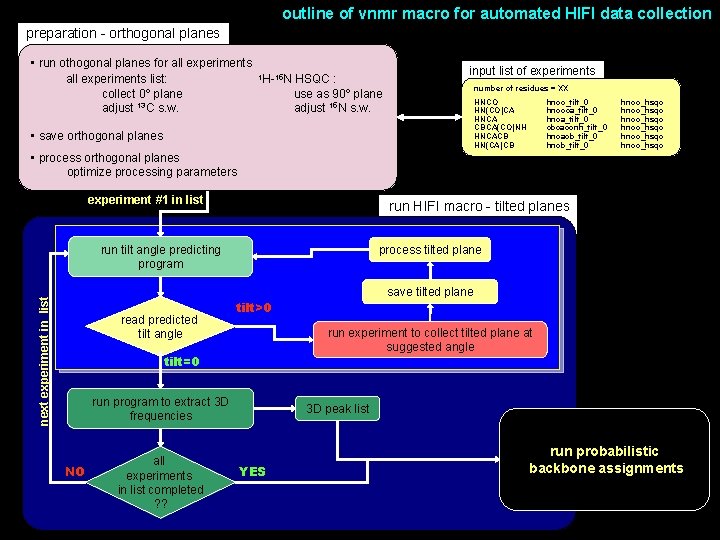
outline of vnmr macro for automated HIFI data collection preparation - orthogonal planes • run othogonal planes for all experiments 1 H-15 N HSQC : all experiments list: collect 0º plane use as 90º plane 13 adjust C s. w. adjust 15 N s. w. input list of experiments number of residues = XX HNCO HN(CO)CA HNCA CBCA(CO)NH HNCACB HN(CA)CB • save orthogonal planes hnco_tilt_0 hncoca_tilt_0 hnca_tilt_0 cbcaconh_tilt_0 hncacb_tilt_0 hnco_hsqc hnco_hsqc • process orthogonal planes optimize processing parameters experiment #1 in list run HIFI macro - tilted planes next experiment in list run tilt angle predicting program read predicted tilt angle process tilted plane run experiment to collect tilted plane at suggested angle tilt=0 run program to extract 3 D frequencies NO all experiments in list completed ? ? save tilted plane tilt>0 3 D peak list YES run probabilistic backbone assignments

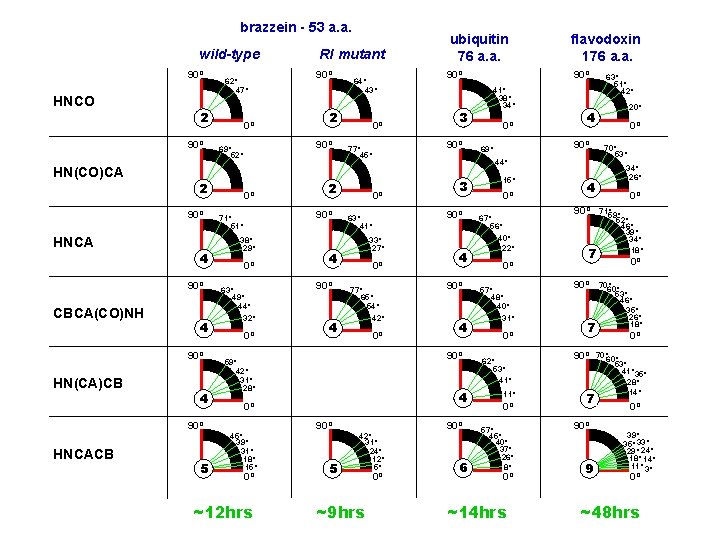
brazzein - 53 a. a. wild-type 90º HNCO 2 90º HN(CO)CA 4 90º CBCA(CO)NH 4 90º HN(CA)CB 0º 4 0º 38º 29º 0º 63º 49º 44º 32º 0º 5 64º 43º 2 0º 90º 33º 27º 0º 77º 65º 54º 42º 0º 90º ~12 hrs 5 4 90º 42º 31º 24º 12º 5º ~9 hrs 0º 0º 15º 6 0º 4 90º 67º 56º 40º 22º 0º 57º 48º 40º 31º 0º 62º 53º 41º 11º 0º 57º 45º 40º 37º 26º 8º 0º ~14 hrs 63º 51º 42º 20º 4 90º 69º 3 4 0º 0º 41º 38º 34º 3 90º 59º 42º 31º 28º 45º 39º 31º 18º 15º 90º 90º 63º 41º 4 flavodoxin 176 a. a. 44º 0º 4 ubiquitin 76 a. a. 90º 77º 45º 2 90º 71º 51º 90º HNCACB 90º 69º 52º 2 90º HNCA 62º 47º RI mutant 7 90º 9 0º 70º 53º 34º 26º 0º 71º 59º 52º 46º 39º 34º 18º 0º 70º 60º 53º 46º 35º 26º 18º 0º 70º 60º 53º 41º 35º 28º 14º 0º 39º 35º 33º 29º 24º 18º 14º 11º 3º 0º ~48 hrs

HIFI backbone assignments - recap we have developed HIFI for extracting 3 D peaks using 2 D tilted planes by adaptively predicting the best tilt angles, we guarantee that all available 3 D data is extracted using the minimum number of tilted planes we have adapted the most robust 3 D experiments for backbone assignments to be recorded using HIFI-NMR we have successfully automated HIFI backbone data collection for proteins of small/medium size automated HIFI is robust and allows to extract 3 D peaks lists with: • least amount of spectrometer time • minimum human intervention

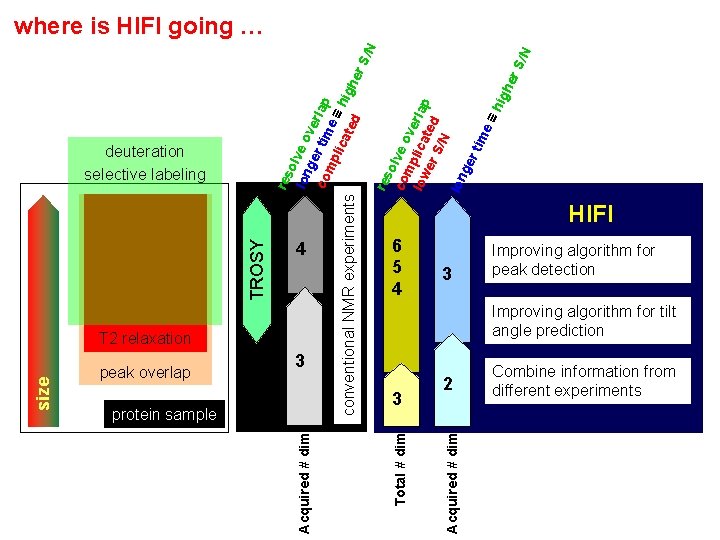
protein sample /N er S res o co lve o m v low plica erlap te er S/N d lon ge r ti me ≡h igh 6 5 4 3 Improving algorithm for peak detection Improving algorithm for tilt angle prediction 3 3 2 Acquired # dim peak overlap HIFI Total # dim size T 2 relaxation 4 Acquired # dim TROSY deuteration selective labeling res o lon lve o ve g co er tim rlap mp lic e ≡ h ate i conventional NMR experiments d gher S/N where is HIFI going … Combine information from different experiments

The BIG picture NMR data collection chemical shift assignments structure calculation

HIFI NMR : part 2 conclusions and other applications Marco Tonelli National Magnetic Resonance Facility At Madison NMRFAM

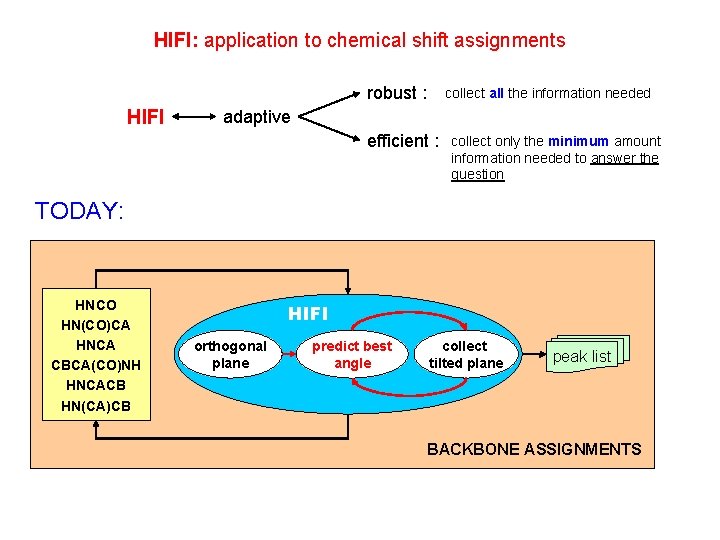
HIFI: application to chemical shift assignments robust : HIFI collect all the information needed adaptive efficient : collect only the minimum amount information needed to answer the question TODAY: HNCO HN(CO)CA HNCA CBCA(CO)NH HNCACB HN(CA)CB HIFI orthogonal plane predict best angle collect tilted plane peak list BACKBONE ASSIGNMENTS

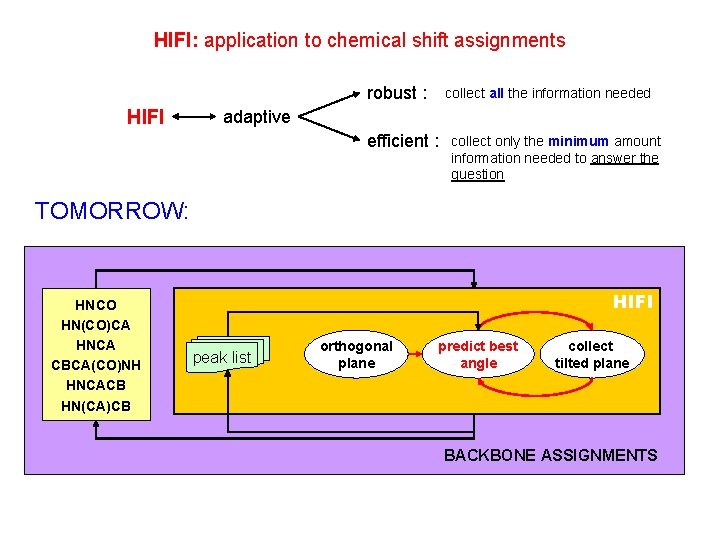
HIFI: application to chemical shift assignments robust : HIFI collect all the information needed adaptive efficient : collect only the minimum amount information needed to answer the question TOMORROW: HNCO HN(CO)CA HNCA CBCA(CO)NH HNCACB HN(CA)CB HIFI peak list orthogonal plane predict best angle collect tilted plane BACKBONE ASSIGNMENTS

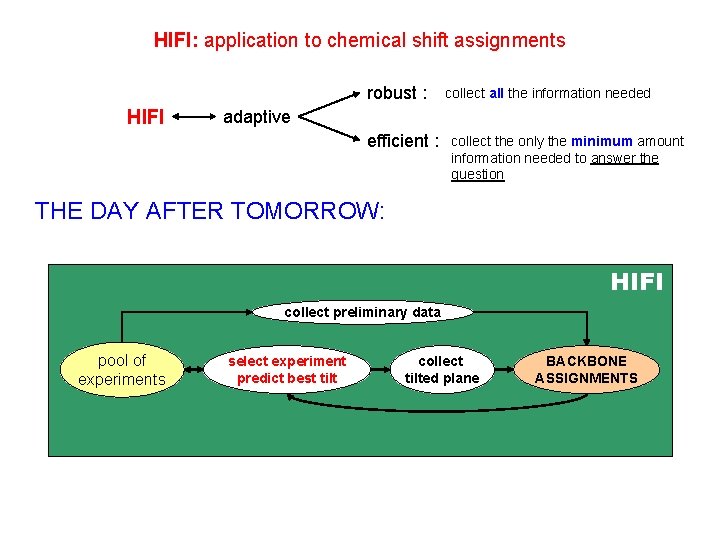
HIFI: application to chemical shift assignments robust : HIFI collect all the information needed adaptive efficient : collect the only the minimum amount information needed to answer the question THE DAY AFTER TOMORROW: HIFI collect preliminary data pool of experiments select experiment predict best tilt collect tilted plane BACKBONE ASSIGNMENTS

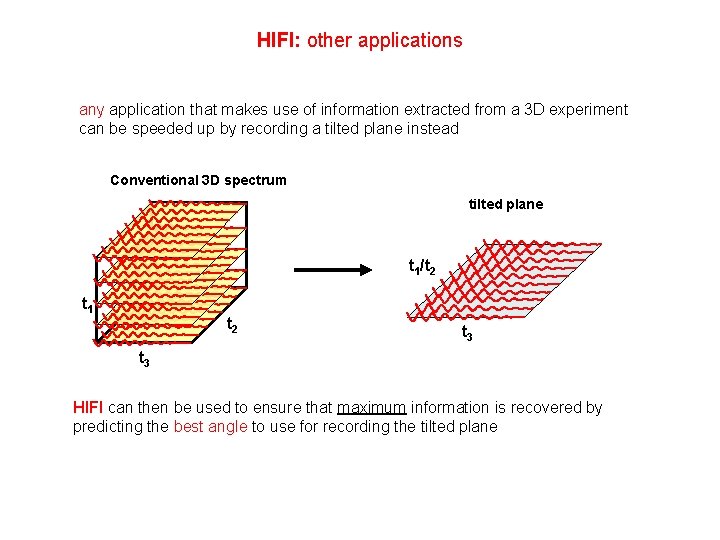
HIFI: other applications any application that makes use of information extracted from a 3 D experiment can be speeded up by recording a tilted plane instead Conventional 3 D spectrum tilted plane t 1/t 2 t 1 t 2 t 3 HIFI can then be used to ensure that maximum information is recovered by predicting the best angle to use for recording the tilted plane

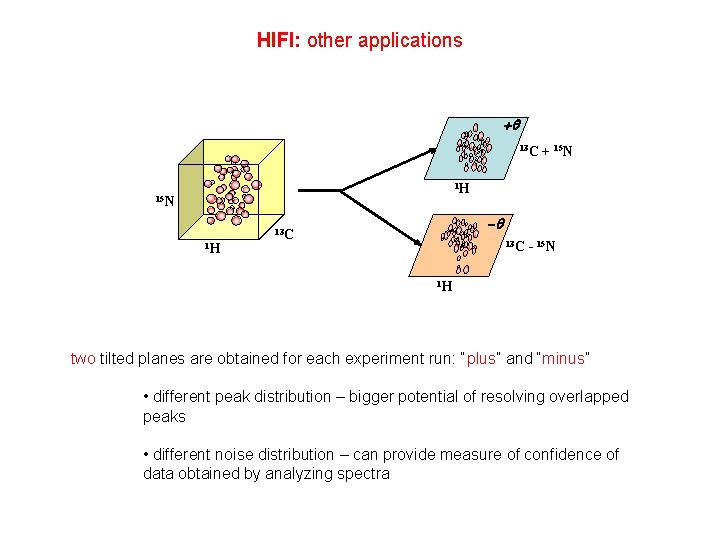
HIFI: other applications +q 13 C + 15 N 1 H -q 13 C - 15 N 1 H two tilted planes are obtained for each experiment run: “plus” and “minus” • different peak distribution – bigger potential of resolving overlapped peaks • different noise distribution – can provide measure of confidence of data obtained by analyzing spectra

HIFI: extraction of RDC Example: extraction of RDCC’N using a modified HNCO pulse sequence (Bax) Conventional method: Ø record two 3 D C’-N-H experiments: 1. reference spectrum 2. attenuated spectrum - intensity of peaks is modulated by coupling: JC’N + DC’N attenuated reference 15 N 1 H 13 C Ø extract JC’N + DC’N coupling from the ratio between intensity of corresponding peaks in the reference and attenuated spectra Ø repeat for isotropic and aligned samples

HIFI: extraction of RDC HIFI method: Ø record two tilted C’-N-H planes at the optimal tilt angle: 1. reference spectrum 2. attenuated spectrum - intensity of peaks is modulated by coupling: JC’N + DC’N reference attenuated +q +q 13 C 1 H reference attenuated -q + 15 N -q 13 C 1 H - 15 N 1 H Ø extract JC’N + DC’N coupling from the ratio between intensity of corresponding peaks in the reference and attenuated spectra Ø analyze “plus” and “minus” planes independently § compare the results from the two plenes to get measure of data confidence § combine the results from the two planes Ø repeat for isotropic and aligned samples 1 H

Who did the work ? tilt prediction and peak extraction algorithms pulse sequences vnmr automation RDC extraction Arash Barhami Hamid Eghbalnia Marco Tonelli Klaas Hallenga Gabriel Cornilescu sample preparation Fariba Assadi-Porter Shanteri Shingh Rob Tyler Anna Fuzery Nick Reiter Claudia Cornilescu John Markley Milo Westler

600 MHz 750 MHz 800 MHz 900 MHz NMRFAM Thank you !