Hierarchical WellSeparated Trees HST Edges distances are uniform

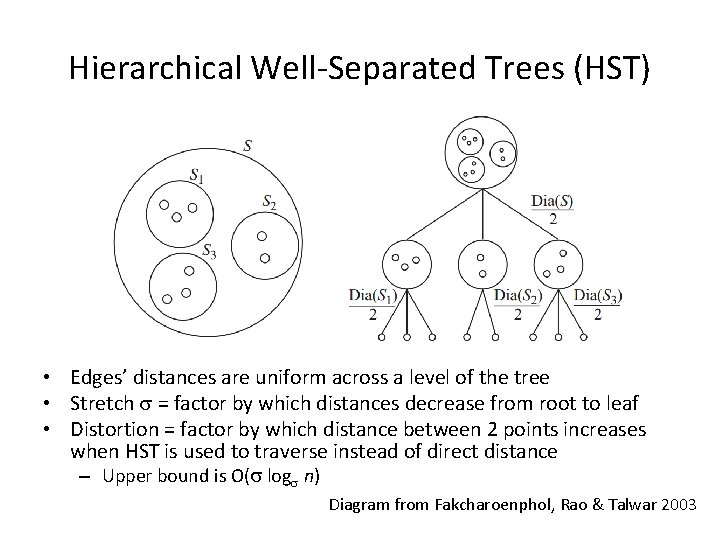
Hierarchical Well-Separated Trees (HST) • Edges’ distances are uniform across a level of the tree • Stretch s = factor by which distances decrease from root to leaf • Distortion = factor by which distance between 2 points increases when HST is used to traverse instead of direct distance – Upper bound is O(s logs n) Diagram from Fakcharoenphol, Rao & Talwar 2003

Pure Randomized vs. Fractional Algorithms • “Fractional view” = keep track only of marginal distributions of some quantities • Lossy compared to pure randomized • Which marginals to track? • Claim: for some algorithms, fractional view can be converted back to randomized algorithm with little loss

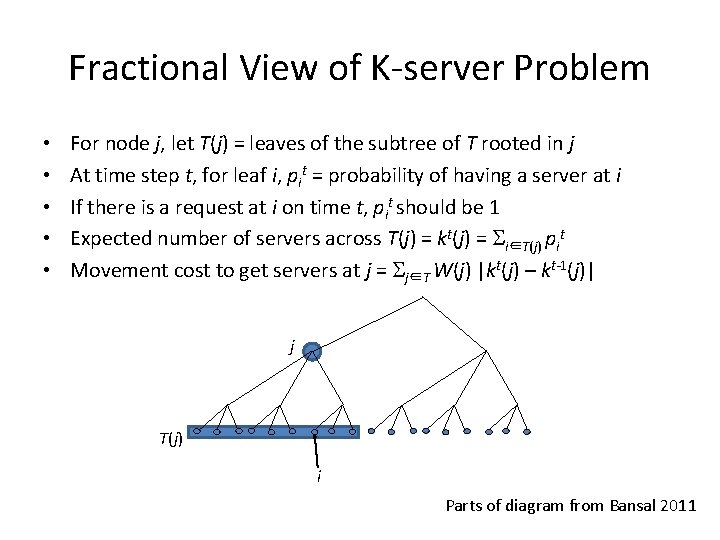
Fractional View of K-server Problem • • • For node j, let T(j) = leaves of the subtree of T rooted in j At time step t, for leaf i, pit = probability of having a server at i If there is a request at i on time t, pit should be 1 Expected number of servers across T(j) = kt(j) = Si∈T(j) pit Movement cost to get servers at j = Sj∈T W(j) |kt(j) – kt-1(j)| j T(j) i Parts of diagram from Bansal 2011

The Allocation Problem • Decide how to (re-)distribute k servers among d locations (each location of uniform distance from a center and may request arbitrary no. of servers) I can work with 1, but I’d like 3! • • Each location i has a request denoted as {ht(0), ht(1), … ht(k)} ht(j) = cost of serving request using j servers Ex. : request at i=0 is {∞, 2, 1, 0, 0} (monotonic decrease) Total cost = hit cost + movement cost Parts of diagram from Bansal 2011

Fractional View of Allocation Problem • Let xi, jt = (non-negative) probability of having j servers at location i at time t • Sum of probabilities Sj xi, jt = 1 • No. of servers used must not exceed no. available Si Sj j ∙ xi, jt ≤ k • Hit cost incurred = Sj ht(j) ∙ xi, jt • Movement cost incurred = Si Sj (|Sj’<j xi, jt – Sj’<j xi, jt-1|) • Note: fractional A. P. too weak to obtain randomized A. P. algorithm – But we don’t really care about A. P. , we care about K-server problem!

From Allocation to K-Server • Theorem 2: It suffices to have a (1+ , ( ))competitive fractional AP algorithm on uniform metric to get a k-server algorithm that is O(βl)-competitive algorithm (Coté et al. 2008) • Theorem 1: Bansal et al. ’s k-server algorithm has a competitive ratio of Õ(log 2 k log 3 n)

The Main Algorithm 1. Embed the n points into a distribution m over s. HSTs with stretch s = Q(log n log(k log n)) – (No time to discuss, this step is essentially from the paper of Fakcharoenphol, Rao & Talwar 2003) 2. According to distribution m, pick a random HST T – Extra step: Transform the HST to a weighted HST (We’ll briefly touch on this) Diagram from Bansal 2011

The Main Algorithm 3. Solve the (fractional) allocation problem on T’s root node + immediate children, then recursively solve the same problem on each child – – Intuitive application of Theorem 2 d = immediate children of a given node At root node: k = all k servers At internal node i: k = resulting (re)allocation of servers from i’s parent Allocation instances Diagram from Bansal 2011

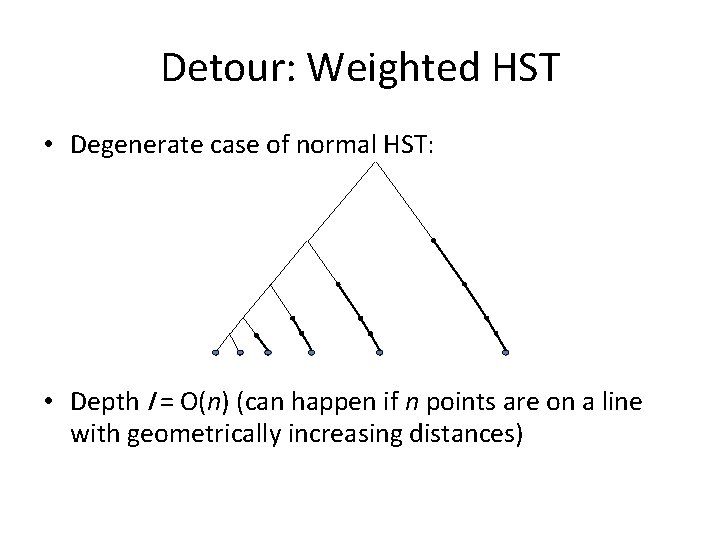
Detour: Weighted HST • Degenerate case of normal HST: • Depth l = O(n) (can happen if n points are on a line with geometrically increasing distances)

Detour: Weighted HST • Solution: allow lengths of edges to be non-uniform • Allow distortion from leaf-to-leaf to be at most 2 s/(s– 1) • Depth l = O(log n) • Consequence: Uniform A. P. becomes weighted-star A. P.

Proving the Main Algorithm • Theorem 1: Bansal et al. ’s k-server algorithm has a competitive ratio of Õ(log 2 k log 3 n) • Idea of proof: How does competitive ratio and distortion evolve as we transform: Fractional allocation algorithm ↓ Fractional k-server algorithm on HST ↓ Randomized k-server algorithm on HST

Supplemental Theorems • Theorem 3: For > 0, there exists a fractional A. P. algorithm on a weighted-star metric that is (1+ , O(log(k/ )))competitive (Refinement of theorem 2, to be discussed by Tanvirul) • Theorem 4: If T is a weighted s-HST with depth l, if Theorem 3 holds, then there is a fractional k-server algorithm that is O(l log(kl))-competitive as long as s = W(l log(kl)) • Theorem 5: If T is a s-HST with s>5, then any fractional kserver algorithm on T converts to a randomized k-server algorithm on T that is about as competitive (only O(1) loss) • Theorem 6: If T is a s-HST with n leaves and any depth, it can transform to a weighted s-HST with identical leaves but with depth O(log n) and leaf-to-leaf distance distorted only by at most 2 s/(s– 1)

Proof of Theorem 1 1. Embed the n points into a distribution m over s. HSTs with stretch s = Q(log n log(k log n)) – – Distortion at O(s logs n) Resulting HSTs may have depth l up to O(n) 2. According to distribution m, pick a random HST T and transform to a weighted HST – – From Theorem 6, depth l reduced to O(log n) Stretch s is now Q(l log (kl)))

Proof of Theorem 1 3. Solve the (fractional) allocation problem on T’s root node + immediate children, then recursively solve the allocation problem on children – – – This is explicitly Theorem 2 refined by Theorem 3 Stretch s = Q(l log (kl))), so Theorem 4 is applicable! – Applying Theorem 5, we get similar competitiveness for the randomized k-server algorithm Transform to a fractional k-server algorithm with competitiveness = O(l log (kl))) = O(log n log (k log n))

Proof of Theorem 1 • Expected distortion to optimal solution Opt*M, given the cost of the solution on T, c. T: Em[c. T ] = O(s logs n) ∙ Opt*M Alg. M ≤ Alg. T ≤ O(log n log (k log n)) ∙ c. T Em[Alg. M ] = O(log n log (k log n)) ∙ Em[c. T ] = O(log n log (k log n)) ∙ O(s logs n) ∙ Opt*M

Proof of Theorem 1 Em[Alg. M ] = O(log n log (k log n)) ∙ O(s logs n) ∙ Opt*M • This implies a competitive ratio of: O(log n log (k log n)) ∙ O(s logs n) = O(log n log (k log n)) ∙ O(s (log n / log s)) = O{[log 3 n (log (k log n))2] / log n} = O(log 2 k log 3 n log n) = Õ(log 2 k log 3 n)