Hierarchical Stability Based Model Selection for Data Clustering

Hierarchical Stability Based Model Selection for Data Clustering Bing Yin Advisor: Greg Hamerly 9/29/2020 1

Roadmap What is clustering? What is model selection for clustering algorithms? Stability Based Model Selection: Proposals and Problems Hierarchical Stability Based Model Selection ● Algorithm ● Unimodality Test ● Experiments Future work Main Contribution ● Extended the concept of stability to hierarchical stability. ● Solved the symmetric data sets problem. ● Make stability a competing tool for model selection. 9/29/2020 2

What is clustering? Given: ● data set of “objects” ● some relations between those objects: similarities, distances, neighborhoods, connections, … Goal: Find meaningful groups of objects s. t. ● objects in the same group are “similar” ● objects in different groups are “dissimilar” Clustering is: ● a form of unsupervised learning ● a method of data exploration 9/29/2020 3

What is clustering? An Example Image Segmentation: Micro array Analysis: Serum Stimulation of Human Fibroblasts (Eisen, Spellman, PNAS, 1998) ● 9800 spots representing 8600 genes ● 12 samples taken over 24 hour period Document Clustering Post-search Grouping Data Mining Social Network Analysis Gene Family Grouping … 9/29/2020 ● Clusters can be roughly categorized as gene involved in A: cholesterol biosynthesis B: the cell cycle C: the immediate-early response D: signaling and angiogenesis E: wound healing and tissue remodeling 4

What is clustering? An Algorithm K-Means algorithm (Lloyd, 1957) Given: data points X 1, …, Xn d, number K clusters to find. 1. Randomly initialize the centers m 10, …, m. K 0. 2. Iterate until convergence: 2. 1 Assign each point to the closest center according to Euclidean distance, i. e. , define clusters C 1 i+1, …, CKi+1 by Xs Cki+1 where ||Xs-mki||2 < ||Xs-mli||2, l=1 to K 2. 2 Compute the new cluster centers by mki+1 = Xs / |Cki+1| What is optimized? Minimizing within-cluster distances: 9/29/2020 5

What is model selection? Clustering algorithms need to know the K before running. The correct answer of K for a given data is unknown So we need a better way to find this K and also the positions of the K centers This can be intuitively called model selection for clustering algorithms. Existing model selection method: ● Bayesian Information Criterion ● Gap statistics ● Projection Test … ● Stability based approach 9/29/2020 6

Stability Based Model Selection The basic idea: ● scientific truth should be reproducible in experiments. Repeatedly run a clustering algorithm on the same data with parameter K and get a collection of clustering: ● If K is the correct model, clustering should be similar to each other ● If K is a wrong model, clustering may be quite different from each other This fact is referred as the stability of K (Ulrike von Luxburg, 2007) 9/29/2020 7

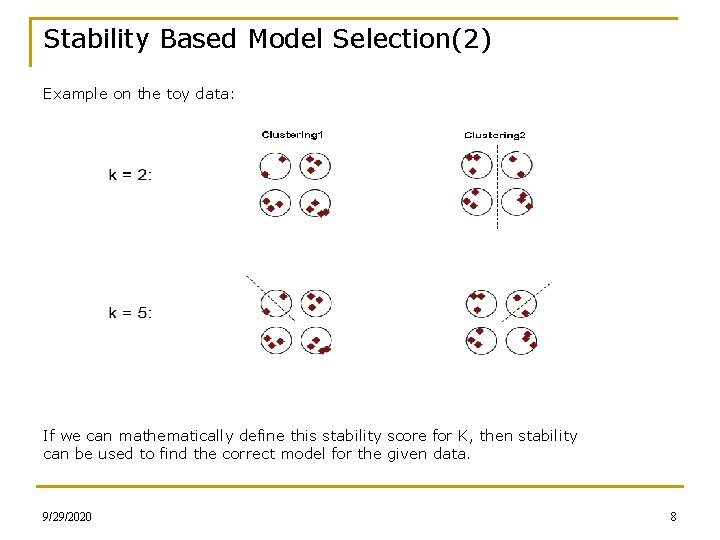
Stability Based Model Selection(2) Example on the toy data: If we can mathematically define this stability score for K, then stability can be used to find the correct model for the given data. 9/29/2020 8

Define the Stability Variation of Information (VI) ● Clustering C 1: X 1, …, Xk and Clustering C 2: X’ 1, …, X’k on date X ● The prob. point p belongs in Xi is : ● The entropy of C 1: ● The joint prob. p in Xi and X’j is P(i, j) with entropy: ● The VI is defined as: VI indicates a distance between two clustering. 9/29/2020 9

Define the stability (2) Calculate the VI score for a single K ● Clustering the data using K-Means for K clusters, run M times ● Calculate pair wise VI of these M clustering. ● Average the VI and use it as the VI score for K The calculated VI score for K indicates instability of K Try this over different K The K with lowest VI score/instability is chosen as the correct model 9/29/2020 10

Define the Stability(3) An good example of Stability An bad example of Stability: symmetric data Why? Because Clustering data into 9 clusters apparently has more grouping choices than clustering them into 3. 9/29/2020 11

Hierarchical Stability Problems with the concept of stability introduced above: ● Symmetric Data Set ● Only local optimization – the smaller K Proposed solution ● Analyze the stability in an hierarchical manner ● Do Unimodality Test to detect the termination of the recursion 9/29/2020 12

Hierarchical Stability Given: Data set X HS-means: ● 1. Test if X is not a unimodal cluster ● 2. If yes, find the optimal K for X by analyzing stability; otherwise, X is a single cluster, return. ● 3. Partition X into K subsets ● 4. For each subset, recursively perform this algorithm from step 1 ● 5. Merge answers from each subset as answer for current data 9/29/2020 13

Unimodality Test - 2 Unimodality test Fact: sum of squared Gaussians follows 2 distribution. ● If x 1, …, xd are d independent Gaussian variables, then S = x 12+…+xd 2 follows 2 distribution of degree d. For given data set X, calculate Si=Xi 12+…+Xid 2 ● If X is a single Gaussian, then S follows 2 of degree d ● Otherwise, S is not a 2 distribution. 9/29/2020 14

Unimodality Test - Gap Test Fact: the within cluster dispersion drops most apparently with the correct K (Tibshirani, 2000) Given: Data set X, candidate k ● cluster X to k clusters and get within cluster dispersion Wk ● generate uniform data sets, cluster to k clusters, calculate W*k (averaged) ● gap(k) = W*k – Wk ● select smallest k s. t. gap(k)>gap(k+1) ● we use it in another way: just ask k=1? 9/29/2020 15

Experiments Synthetic data ● Both Gaussian Distribution and Uniform Distribution ● In dimensions from 2 up to 20 ● c-separation between each cluster center and its nearest neighbor is 4 ● 200 points in each cluster, 10 clusters in total Handwritten Digits ● U. S. Postal Service handwritten digits ● 9298 instances in 256 dimensions ● 10 true clusters (maybe!) KDDD Control Curves ● 600 instances in 60 dimensions ● 6 true clusters, each has 100 instances Synthetic Gaussian (10 true clusters) Synthetic Uniform (10 true clusters) Handwritten Digits (10 true clusters) KDDD Control Curves (6 true clusters) HS-means 10 1 6 0 6. 5 0. 5 Lange Stability 6. 5 1. 5 7 1 2 0 3 0 PG-means 10 1 19. 5 1. 5 20 1 17 1 9/29/2020 16

Experiments – symmetric data HS-means 9/29/2020 Lange Stability 17

Future Work ● Better Unimodality Testing approach. ● More detailed comparison on the performance with existing method like within cluster distance, VI metric and so on. ● Improve the speed of the algorithm. 9/29/2020 18

n Questions and Comments Thank you! 9/29/2020 19