Hierarchical Reinforcement Learning HRL Jacob Dineen Matthew Bielskas

Hierarchical Reinforcement Learning (HRL) Jacob Dineen, Matthew Bielskas, Ahsan Tarique CS @ UVA November 5 th, 2020

Outline • Hierarchical Reinforcement Learning with the MAXQ Value Function Decomposition • Learning Multi-Level Hierarchies with Hindsight CS@UVA RL 2020 -Fall 2

HRL with the MAXQ Value Function Decomposition [1] Thomas G. Dietterich. 1999 CS@UVA RL 2020 -Fall 3

Introduction • Most tasks are defined by a set of subtasks needed to be achieved to accomplish them. • E. g. , brushing your teeth involves navigation, picking up and dropping off objects, and brushing itself • CS@UVA Solving the main task solves all necessary subtasks. • Hierarchical Reinforcement Learning is attractive for problems with a natural decomposition RL 2020 -Fall 4

Motivation • (1998) Reinforcement Learning/Dynamic Programming algorithms were not scalable. • Hierarchical methods were shown to provide exponential reductions in compute for reasoning, control and planning tasks in recent years (: 1998). • Hierarchical decomposition mirrors some aspects of human cognition (temporal abstraction). • Identify a task -> break into subtasks -> complete root task • Constrains the set of policies that need to be considered • Allows for faster learning & structured exploration. CS@UVA RL 2020 -Fall 5

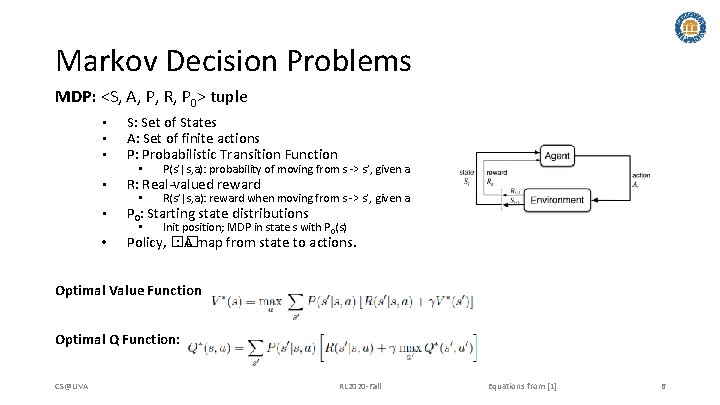
Markov Decision Problems MDP: <S, A, P, R, P 0> tuple • • • S: Set of States A: Set of finite actions P: Probabilistic Transition Function • P(s’|s, a): probability of moving from s -> s’, given a • R(s’|s, a): reward when moving from s -> s’, given a • Init position; MDP in state s with P 0(s) R: Real-valued reward P 0: Starting state distributions Policy, �� : A map from state to actions. Optimal Value Function: Optimal Q Function: CS@UVA RL 2020 -Fall Equations from [1] 6

Markov Decision Problems Semi Markov Decision Process (SMDP) • Generalizes MDPs to account for time to take an action • N: Number of steps that action a takes when executed in s • Transition function: P(s’|s, a) -> P(s’, N|s, a) • Reward function: R(s’|s, a) -> R(s’, N|s, a) Modified Value Function: CS@UVA RL 2020 -Fall Equations from [1] 7

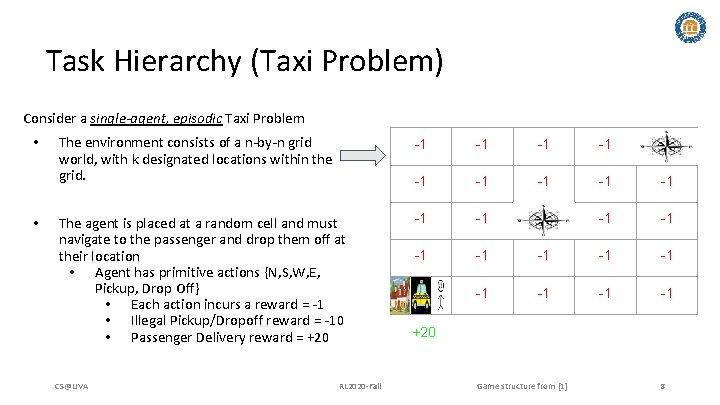
Task Hierarchy (Taxi Problem) Consider a single-agent, episodic Taxi Problem • • The environment consists of a n-by-n grid world, with k designated locations within the grid. -1 -1 -1 The agent is placed at a random cell and must navigate to the passenger and drop them off at their location • Agent has primitive actions {N, S, W, E, Pickup, Drop Off} • Each action incurs a reward = -1 • Illegal Pickup/Dropoff reward = -10 • Passenger Delivery reward = +20 -1 -1 -1 -1 CS@UVA RL 2020 -Fall +20 Game structure from [1] 8

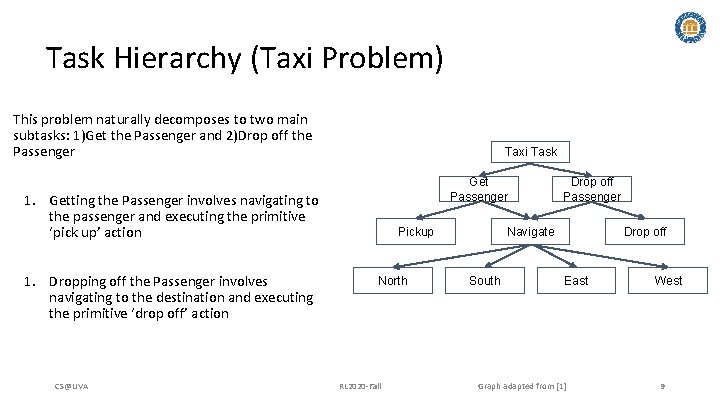
Task Hierarchy (Taxi Problem) This problem naturally decomposes to two main subtasks: 1)Get the Passenger and 2)Drop off the Passenger Taxi Task Get Passenger 1. Getting the Passenger involves navigating to the passenger and executing the primitive ‘pick up’ action 1. Dropping off the Passenger involves navigating to the destination and executing the primitive ‘drop off’ action CS@UVA Pickup North RL 2020 -Fall Drop off Passenger Navigate South Drop off East Graph adapted from [1] West 9

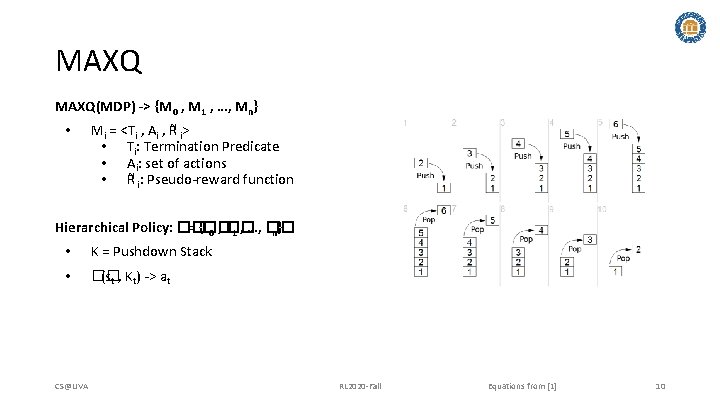
MAXQ(MDP) -> {M 0 , M 1 , …, Mn} • Mi = <Ti , Ai , R i> • Ti: Termination Predicate • Ai: set of actions • R i: Pseudo-reward function Hierarchical Policy: �� = {�� 0 , �� 1 , …, �� n} • K = Pushdown Stack • �� (st , Kt) -> at CS@UVA RL 2020 -Fall Equations from [1] 10

Decomposing the Hierarchical Value Function Projected Value Function: Decomposition Equations Completion Function: Q Function: Projected Value Function: CS@UVA RL 2020 -Fall Equations from [1] 11

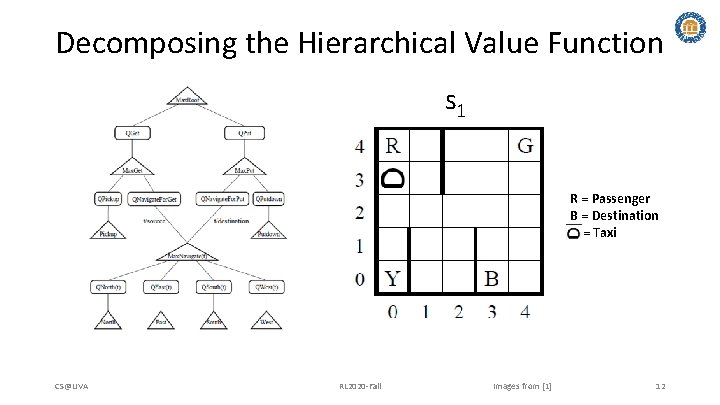
Decomposing the Hierarchical Value Function s 1 R = Passenger B = Destination = Taxi CS@UVA RL 2020 -Fall Images from [1] 12

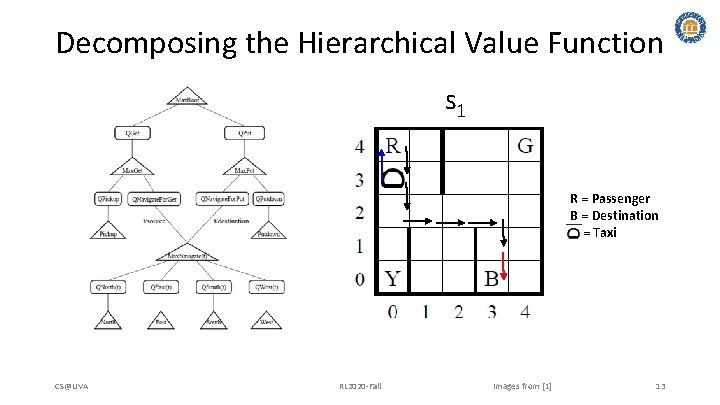
Decomposing the Hierarchical Value Function s 1 R = Passenger B = Destination = Taxi CS@UVA RL 2020 -Fall Images from [1] 13

Decomposing the Hierarchical Value Function V�� (Root, s 1) = CS@UVA RL 2020 -Fall Images from [1] 14

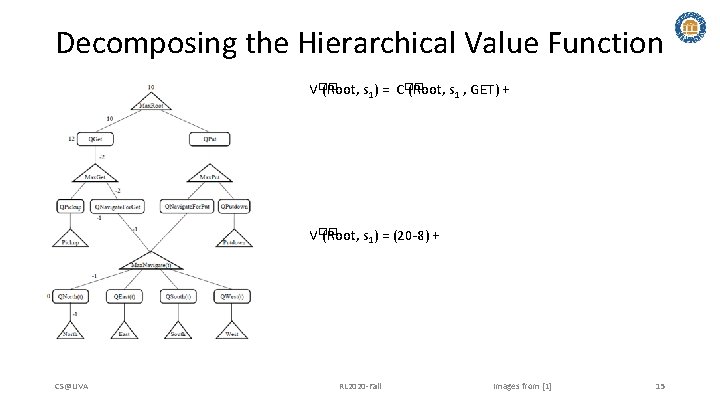
Decomposing the Hierarchical Value Function V�� (Root, s 1) = C�� (Root, s 1 , GET) + V�� (Root, s 1) = (20 -8) + CS@UVA RL 2020 -Fall Images from [1] 15

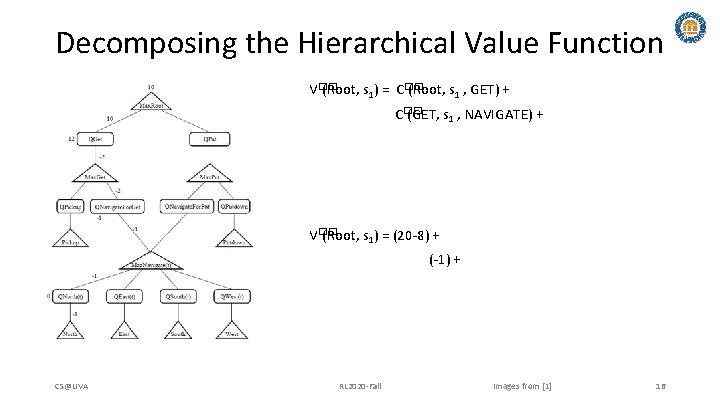
Decomposing the Hierarchical Value Function V�� (Root, s 1) = C�� (Root, s 1 , GET) + C�� (GET, s 1 , NAVIGATE) + V�� (Root, s 1) = (20 -8) + (-1) + CS@UVA RL 2020 -Fall Images from [1] 16

Decomposing the Hierarchical Value Function V�� (Root, s 1) = C�� (Root, s 1 , GET) + C�� (GET, s 1 , NAVIGATE) + C�� (NAVIGATE(R), s 1 , NORTH) + V�� (Root, s 1) = (20 -8) + (-1) + (0) + CS@UVA RL 2020 -Fall Images from [1] 17

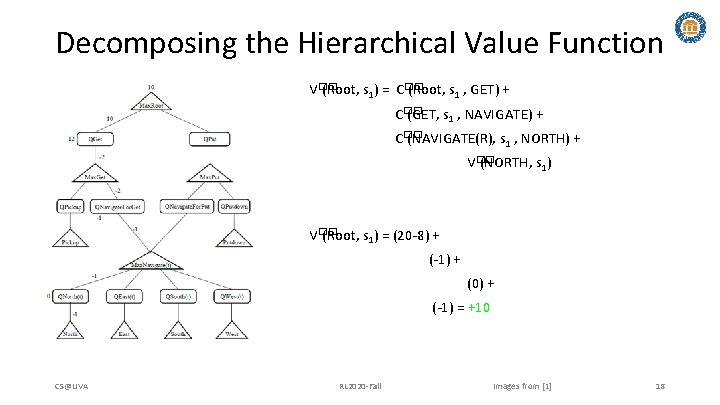
Decomposing the Hierarchical Value Function V�� (Root, s 1) = C�� (Root, s 1 , GET) + C�� (GET, s 1 , NAVIGATE) + C�� (NAVIGATE(R), s 1 , NORTH) + V�� (NORTH, s 1) V�� (Root, s 1) = (20 -8) + (-1) + (0) + (-1) = +10 CS@UVA RL 2020 -Fall Images from [1] 18

Optimality • Constraints may lead to non-optimal policy • Hierarchically optimal: highest cumulative reward among all policies consistent with the given hierarchy. • Recursively optimal: for each subtask Mi , the corresponding policy πi is optimal for the SMDP defined by the states Si , actions Ai , transition probability function P π (s ′ , N|s, a), the reward function R(s ′ |s, a) and the pseudo-reward function R i(s ′ ) CS@UVA RL 2020 -Fall 19

MAXQ-0 Terminal state

MAXQ-Q

State Abstraction • Within each subtask, we can ignore certain aspects of the state space • At each Max node i, suppose the state variables are partitioned into two sets Xi and Yi , and let χi be a function that projects a state s onto only the values of the variables in Xi • Max. Q graph H combined with χi is called a state-abstracted MAXQ graph

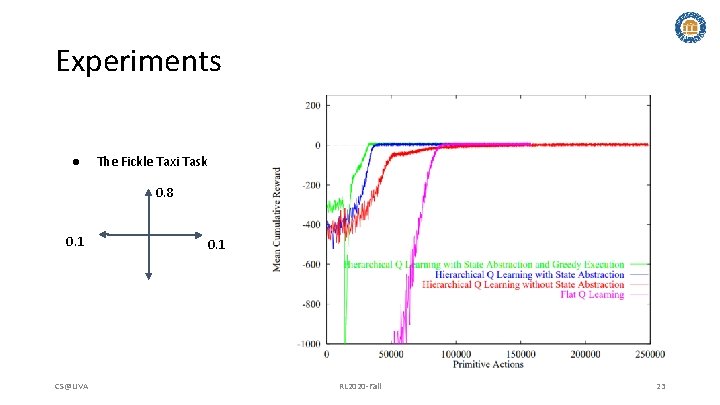
Experiments ● The Fickle Taxi Task 0. 8 0. 1 CS@UVA 0. 1 RL 2020 -Fall 23

Challenges • Learned Policy may be suboptimal. • Approaches guarantee that policy learned will be best possible of constrained policies. • MAXQ does not learn the structure of the hierarchy. • Influenced by Belief Networks; The structure is provided by knowledge engineers/domain experts CS@UVA RL 2020 -Fall 24

Conclusion • Introduced new representation for value function in HRL • • Offers state abstraction Introduced learning algorithm MAXQ-Q, converges to optimal recursive policy • Each subtask learns locally optimal policy ignoring ancestors in task graph • Exploits state abstraction and enables speed ups and subtask sharing CS@UVA RL 2020 -Fall 25

Learning Multi-Level Hierarchies with Hindsight [3] Andrew Levy, George Konidaris, Robert Platt, and Kate Saenko CS@UVA RL 2020 -Fall 26

Continuous HRL- Bottom-up vs. Parallel ● It would be efficient to learn hierarchy levels in parallel ● An issue is that levels are dependent on those below them ○ ○ ● Transition functions are nonstationary (above ground level) It is difficult to evaluate actions Previous work in the continuous setting mainly settled on learning lower levels first, e. g. Skill Chaining (Konidaris & Barto)

Hierarchical Actor-Critic (HAC) Overview ● ● HAC is designed to solve Universal MDPs U=(S, G, A, T, R, γ), where G is a set of goals, by learning levels in parallel. It achieves this with a nested hierarchical structure, so that the state space breaks tasks into subtasks (finite H attempts per level) ○ Result: k UMDPs Ui=(Si, Gi, Ai, Ti, Ri, γi) ● Hindsight transitions are introduced to facilitate learning in the presence of sparse rewards

Actor-Critic We train actor functions Πi and critic functions Qi for each level i ● Actor- Est. Policy, Critic- Est. Q-values ● HAC is built upon the DDPG algorithm ○ ○ ○ Deterministic target policy; off-policy learning Experience Replay: “Replay Buffer” HAC bounds Q-values: [-H, 0]

HAC Architecture- In Action CS@UVA RL 2020 -Fall 30

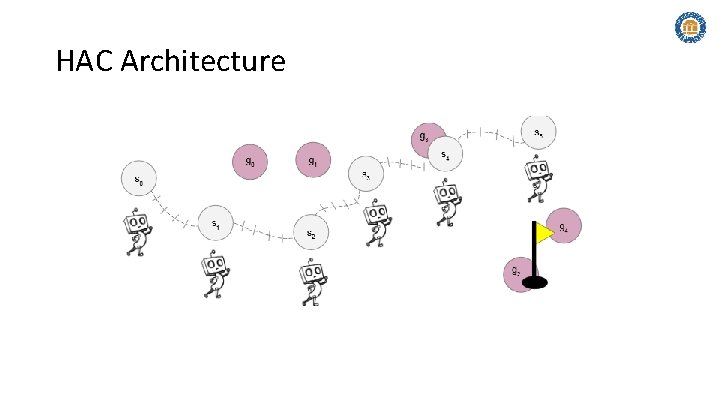
HAC Architecture

Hindsight Action Transitions To overcome nonstationarity, Hindsight Action Transitions allow us to simulate a transition function that uses the optimal lower-level policy 1. Action A is the subgoal state achieved in hindsight. 1. Reward function: Incentivize shorter paths (for faster learning) and ensure level independence. At level i, the agent can find subgoals feasible within some # of actions.

Hindsight Goal Transitions Accelerates learning sparse reward tasks: (Hindsight Experience Replay) 1. At the bottom level, transitions are primitive actions e. g (s_init= s 0 , action= a, r=-1, s_next= first tick, goal= g 0 , discount= γ) 1. Take at most H primitive actions. For the final transition, replace goal with hindsight goal and reward=0 e. g (s_init= s 0 , action= a, r=0, s_next= s 1, goal= s 1 , discount= 0) 1. Higher-level Hindsight Goal Transitions similarly build upon lower ones Common Reward -> Higher Q-values outside of subgoals -> Discovery

Subgoal Testing Transitions- Why? The agent is restricted to a fixed number of actions per level. ● ● Q-learning with a universal function approximator e. g Deep NN What if the agent sets subgoals unachievable by the lower hierarchy? Are Hindsight Action/Goal transitions enough?

Subgoal Testing Transitions- How Solution: Subgoal Testing Transitions. Let level i propose subgoal ai. Prob λ: follow current Πi− 1 (w/o noise) Prob 1 -λ: “Optimal” Πi− 1 (hindsight) ● Current policy and H lower-level actions don’t reach the subgoal: Reward = -H ● Current policy reaches the subgoal: Reward from other transitions ● Optimal policy reaches subgoal, not current policy: Weighted Average

HAC Algorithm

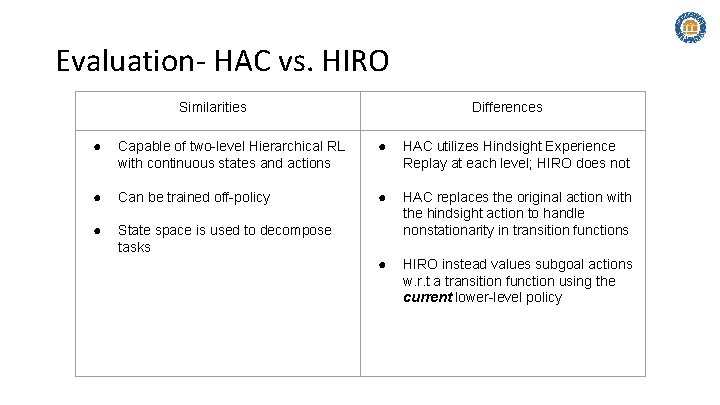
Evaluation- HAC vs. HIRO Similarities Differences ● Capable of two-level Hierarchical RL with continuous states and actions ● HAC utilizes Hindsight Experience Replay at each level; HIRO does not ● Can be trained off-policy ● ● State space is used to decompose tasks HAC replaces the original action with the hindsight action to handle nonstationarity in transition functions ● HIRO instead values subgoal actions w. r. t a transition function using the current lower-level policy

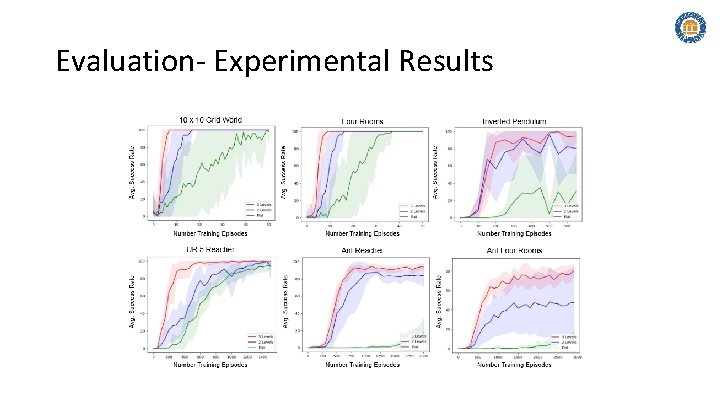
Evaluation- Experimental Results

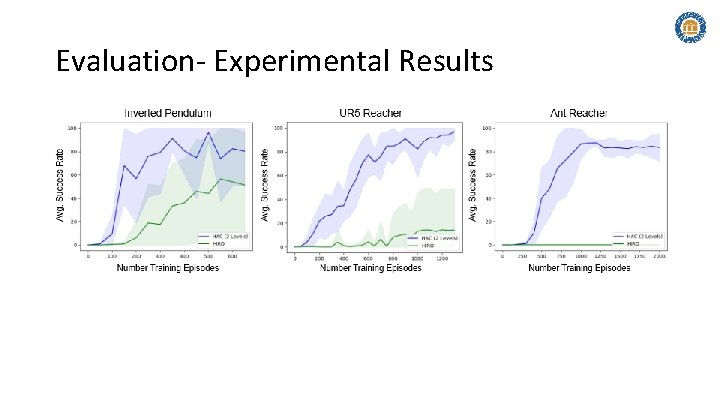
Evaluation- Experimental Results

References [1] Thomas G. Dietterich. 1999. Hierarchical Reinforcement Learning with the MAXQ Value Function Decomposition. ar. Xiv: cs/9905014(May 1999). http: //arxiv. org/abs/cs/9905014 ar. Xiv: cs/9905014. [2] Andrew G Barto and Sridhar Mahadevan. [n. d. ]. Recent Advances in Hierarchical Reinforcement Learning. Discrete Event Dynamic Systems([n. d. ]), 37. [3] Andrew Levy, George Konidaris, Robert Platt, and Kate Saenko. 2019. Learning Multi-Level Hierarchies with Hindsight. ar. Xiv: 1712. 00948 [cs](Sep 2019). http: //arxiv. org/abs/1712. 00948 ar. Xiv: 1712. 00948. CS@UVA RL 2020 -Fall 40

Suggested Readings [4]Marcin Andrychowicz, Filip Wolski, Alex Ray, Jonas Schneider, Rachel Fong, Peter Welinder, Bob Mc. Grew, Josh Tobin, Pieter Abbeel, and Wojciech. Zaremba. 2018. Hindsight Experience Replay. ar. Xiv: 1707. 01495 [cs](Feb 2018). http: //arxiv. org/abs/1707. 01495 ar. Xiv: 1707. 01495. [5]Pierre-Luc Bacon, Jean Harb, and Doina Precup. 2016. The Option-Critic Architecture. ar. Xiv: 1609. 05140 [cs](Dec 2016). http: //arxiv. org/abs/1609. 05140 ar. Xiv: 1609. 05140. [6]Andrew G Barto and Sridhar Mahadevan. [n. d. ]. Recent Advances in Hierarchical Reinforcement Learning. Discrete Event Dynamic Systems([n. d. ]), 37. [7]E. Bonabeau. 2002. Agent-based modeling: Methods and techniques for simulating human systems. Proceedings of the National Academy of Sciences 99, Supplement 3 (May 2002), 7280 7287. https: //doi. org/10. 1073/pnas. 082080899 [8] Craig Boutilier. [n. d. ]. Planning, Learning and Coordination in Multiagent Decision Processes. ([n. d. ]), 16. [9] Caroline Claus and Craig Boutilier. [n. d. ]. The Dynamics of Reinforcement Learning in Cooperative Multiagent Systems. ([n. d. ]), 7. [10] Mohammad Ghavamzadeh. [n. d. ]. Hierarchical Multi-Agent Reinforcement Learning. ([n. d. ]), 44. [11]Mohammad Ghavamzadeh and Sridhar Mahadevan. 2003. Hierarchical Average Reward Reinforcement Learning: . https: //doi. org/10. 21236/ADA 445728 [12]Dongge Han, Wendelin Boehmer, Michael Wooldridge, and Alex Rogers. 2019. Multi-agent Hierarchical Reinforcement Learning with Dynamic. Termination. ar. Xiv: 1910. 09508 [cs]11671 (2019), 80– 92. https: //doi. org/10. 1007/978 -3 -030 -29911 -8_7 ar. Xiv: 1910. 09508. [13] Bernhard Hengst. 2010. Hierarchical Reinforcement Learning. Springer US, Boston, MA, 495– 502. https: //doi. org/10. 1007/978 -0 -387 -30164 -8_363 [14]Andrew Levy, George Konidaris, Robert Platt, and Kate Saenko. 2019. Learning Multi-Level Hierarchies with Hindsight. ar. Xiv: 1712. 00948 [cs](Sep 2019). http: //arxiv. org/abs/1712. 00948 ar. Xiv: 1712. 00948. [15] Ofir Nachum. [n. d. ]. Data-Efficient Hierarchical Reinforcement Learning. ([n. d. ]), 11. [16]Frank Röder, Manfred Eppe, Phuong D. H. Nguyen, and Stefan Wermter. 2020. Curious Hierarchical Actor-Critic Reinforcement Learning. ar. Xiv: 2005. 03420 [cs, stat](Aug 2020). http: //arxiv. org/abs/2005. 03420 ar. Xiv: 2005. 03420. [17]Tom Schaul, John Quan, Ioannis Antonoglou, and David Silver. 2016. Prioritized Experience Replay. ar. Xiv: 1511. 05952 [cs](Feb 2016). http: //arxiv. org/abs/1511. 05952 ar. Xiv: 1511. 05952. [18]Hongyao Tang, Jianye Hao, Tangjie Lv, Yingfeng Chen, Zongzhang Zhang, Hangtian Jia, Chunxu Ren, Yan Zheng, Zhaopeng Meng, Changjie. Fan, and et al. 2019. Hierarchical Deep Multiagent Reinforcement Learning with Temporal Abstraction. ar. Xiv: 1809. 09332 [cs](Jul 2019). http: //arxiv. org/abs/1809. 09332 ar. Xiv: 1809. 09332 CS@UVA RL 2020 -Fall 41