Hierarchical Method ROCK RObust Clustering using Lin Ks

Hierarchical Method ROCK- RObust Clustering using Lin. Ks Ajith G. S: poposir. orgfree. com

Hierarchical Method ROCK- RObust Clustering using Lin. Ks • Distance functions do not lead to high quality clusters when clustering categorical data. • Most clustering techniques assess the similarity between points to create clusters. • At each step, points that are similar are merged into a single cluster This approach is prone to errors. • ROCK: uses links instead of distances and used in the clustering of categorical attributes. Ajith G. S: poposir. orgfree. com

Hierarchical Method ROCK- RObust Clustering using Lin. Ks • ROCK considers the neighbourhoods of individual pairs of points • If two similar points also have similar neighbourhoods, then the two points likely belong to the same cluster and so can be merged. • Two points, pi and pj, are neighbours • if sim(pi, pj) ≥ �, where sim is a similarity function and �is a user-specified threshold • sim can be a distance metric or even a nonmetric fall between 0 and 1, with larger values indicating that the points are more similar. Ajith G. S: poposir. orgfree. com

Hierarchical Method ROCK- RObust Clustering using Lin. Ks • The number of links between pi and pj is defined as the number of common neighbours between pi and pj. • If the number of links between two points is large, then it is more likely that they belong to the same cluster. Ajith G. S: poposir. orgfree. com

Hierarchical Method ROCK- RObust Clustering using Lin. Ks • Similarity between 2 points or transactions Ti and Tj is defined with the Jaccard Coefficient as Ajith G. S: poposir. orgfree. com

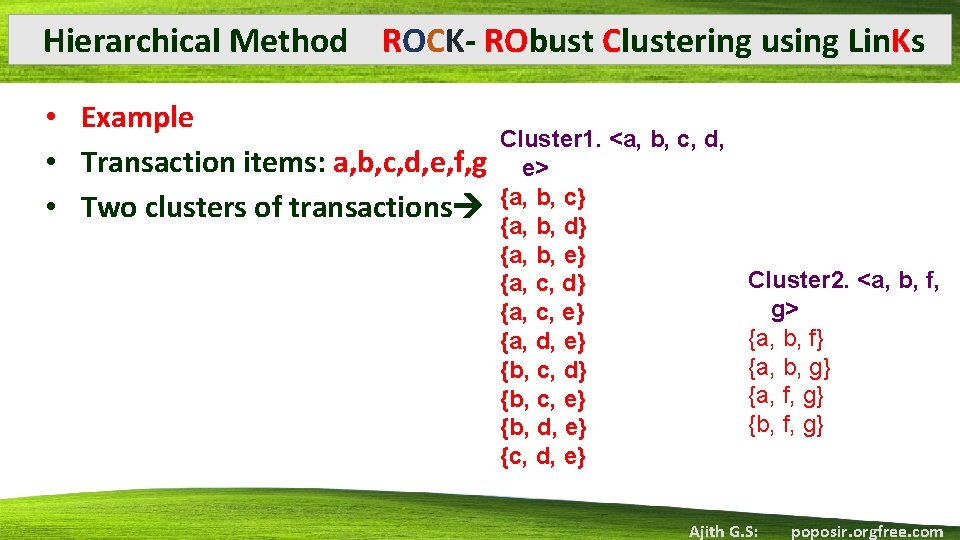
Hierarchical Method ROCK- RObust Clustering using Lin. Ks • Example • Transaction items: a, b, c, d, e, f, g • Two clusters of transactions Cluster 1. <a, b, c, d, e> {a, b, c} {a, b, d} {a, b, e} {a, c, d} {a, c, e} {a, d, e} {b, c, d} {b, c, e} {b, d, e} {c, d, e} Cluster 2. <a, b, f, g> {a, b, f} {a, b, g} {a, f, g} {b, f, g} Ajith G. S: poposir. orgfree. com

Hierarchical Method ROCK- RObust Clustering using Lin. Ks • Example using Jaccard Coefficient • • • Similarity of 2 transactions in cluster 1 Sim({a, b, c}, {a, b, d})=2/4=0. 5 Jaccard coefficient between transactions of Cluster 1 ranges from 0. 2 to 0. 5 Similarity of 2 transactions in cluster 1 and 2 Sim({a, b, c}, {a, b, f})=2/4=0. 5 Jaccard coefficient between transactions belonging to different clusters can also reach 0. 5 Cluster 1. <a, b, c, d, e> {a, b, c} {a, b, d} {a, b, e} {a, c, d} {a, c, e} {a, d, e} {b, c, d} Cluster 2. <a, b, f, {b, c, e} g> {b, d, e} {a, b, f} {c, d, e} {a, b, g} {a, f, g} {b, f, g} Ajith G. S: poposir. orgfree. com

Hierarchical Method ROCK- RObust Clustering using Lin. Ks • Example using Link • • • Cluster 1. <a, b, c, d, e> The number of links between Ti and Tj is the number of {a, b, c} common neighbors {a, b, d} Within the same cluster the transactions will have {a, b, e} most number of links {a, c, d} Ti and Tj are neighbors if Sim(Ti, Tj)> � {a, c, e} Consider Link({a, b, f}, {a, b, g}) = 5 {a, d, e} {b, c, d} Link({a, b, f}, {a, b, c})=3 {b, c, e} Cluster 2. <a, b, f, Link is a better measure than Jaccard coefficient {b, d, e} g> {c, d, e} {a, b, f} {a, b, g} {a, f, g} {b, f, g} Ajith G. S: poposir. orgfree. com

Chameleon: A Hierarchical Clustering Algorithm Using Dynamic Modeling • Uses dynamic modeling to determine the similarity between pairs of clusters. • To overcome the weaknesses of ROCK and CURE • ROCK cluster interconnectivity while ignoring cluster proximity. • CURE cluster proximity yet ignore cluster interconnectivity. • In Chameleon two clusters are merged if their interconnectivity is high and they are close together • Facilitates the discovery of natural and homogeneous clusters and applies to all types of data Ajith G. S: poposir. orgfree. com

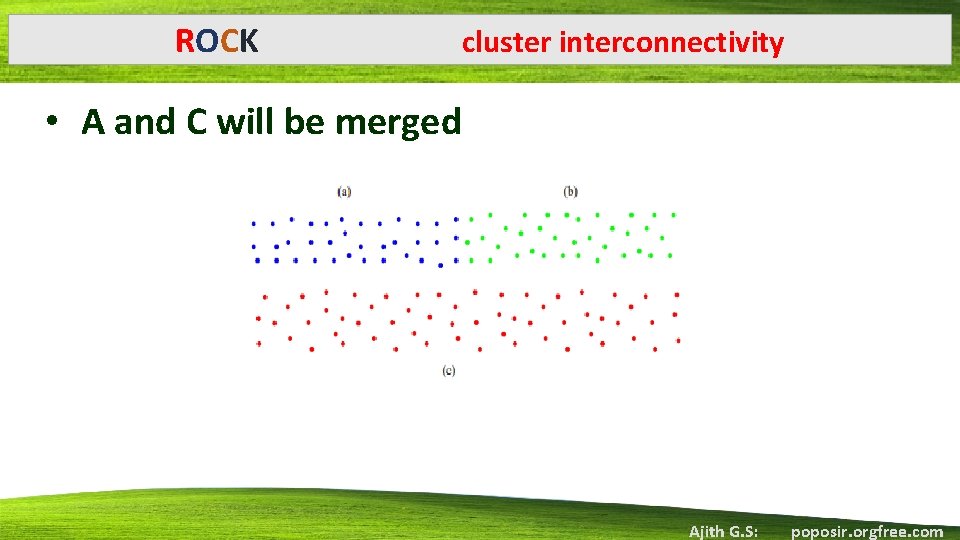
ROCK cluster interconnectivity • A and C will be merged Ajith G. S: poposir. orgfree. com

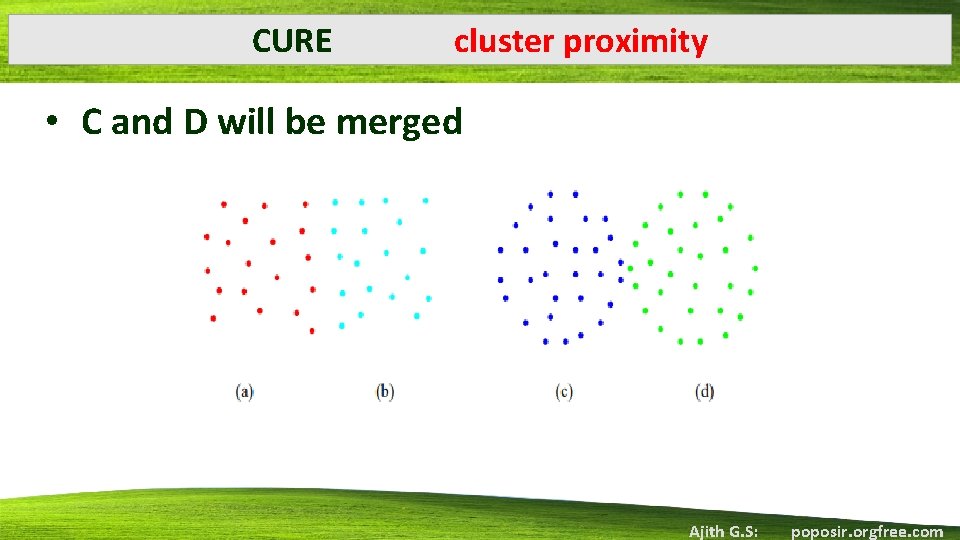
CURE cluster proximity • C and D will be merged Ajith G. S: poposir. orgfree. com

Hierarchical Method Chameleon Working • Constructs a sparse graph based on the k-nearest neighbour graph approach • Nodes represent data items • Weighted edges represent similarities among the data items. Ajith G. S: poposir. orgfree. com

Hierarchical Method Chameleon Working • CHAMELEON finds the clusters in the data set by using a two phase algorithm. • first phase CHAMELEON uses a graph partitioning algorithm to cluster the data items into a large number of relatively small sub-clusters. • second phase it uses an agglomerative hierarchical clustering algorithm to find the genuine clusters by repeatedly combining together these sub-clusters. Ajith G. S: poposir. orgfree. com

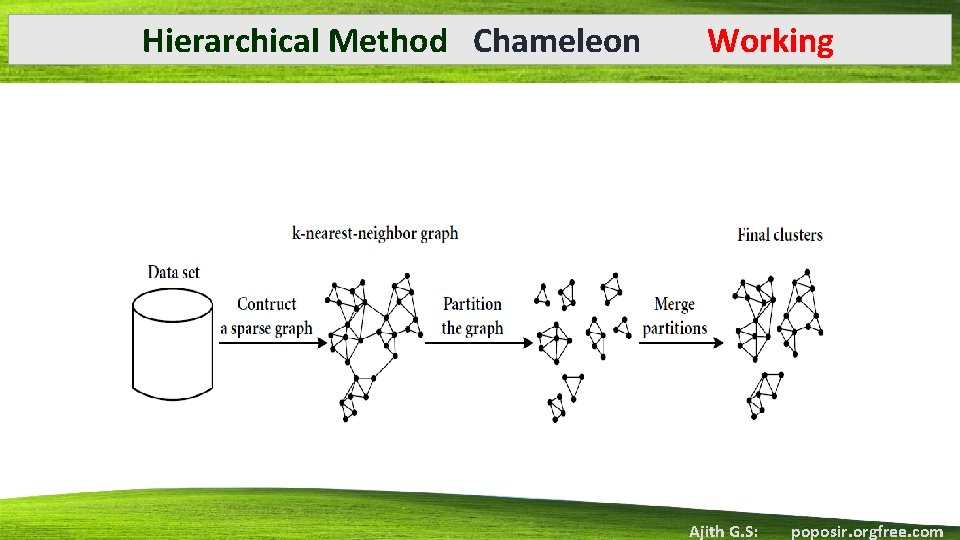
Hierarchical Method Chameleon Working Ajith G. S: poposir. orgfree. com

Hierarchical Method Chameleon PHASE 1 • Sparse graph representation of the data items is based on k-nearest neighbour graph approach. • Each vertex of the graph represents a data item • There exists an edge between two vertices, if data items corresponding to either of the nodes is among the k-most similar data points of the data point corresponding to the other node. Ajith G. S: poposir. orgfree. com

Hierarchical Method Chameleon PHASE 1 • The graph-partitioning algorithm partitions the knearest-neighbor graph such that it minimizes the edge cut cluster C is partitioned into sub clusters Ci and Cj so as to minimize the weight of the edges that would be cut • Edge cut is denoted EC(Ci, Cj) and assesses the absolute interconnectivity between clusters Ci and Cj. Ajith G. S: poposir. orgfree. com

Hierarchical Method Chameleon PHASE 2 • The key feature of CHAMELEON’s agglomerative hierarchical clustering algorithm is that it determines the pair of most similar sub-clusters • by taking into account both the inter-connectivity as well as the closeness of the clusters Ajith G. S: poposir. orgfree. com

Hierarchical Method Chameleon Relative Inter-Connectivity • The relative interconnectivity, between two clusters, Ci and Cj, is defined as the absolute interconnectivity between Ci and Cj, normalized with respect to the internal interconnectivity of the two clusters, Ci and Cj. • EC{Ci, Cj} is the edge cut, for a cluster containing both Ci and Cj. • Similarly, ECCi (or ECCj ) is the minimum sum of the cut edges that partition Ci (or Cj) into two roughly equal parts Ajith G. S: poposir. orgfree. com

Hierarchical Method Chameleon Relative Closeness • The relative closeness, between a pair of clusters, Ci and Cj, is the absolute closeness between Ci and Cj, normalized with respect to the internal closeness of the two clusters, Ci and Cj. • where S EC{ci, cj} is the average weight of the edges that connect vertices in Ci to vertices in Cj • SEcci (or SECcj) is the average weight of the edges that belong to the mincut bisector of cluster Ci (or Cj). Ajith G. S: poposir. orgfree. com