Hierarchical Fault Collapsing Functional Equivalences and Dominances Vishwani









- Slides: 23

Hierarchical Fault Collapsing; Functional Equivalences and Dominances Vishwani D. Agrawal Rutgers University, Dept. of ECE vishwani 02@yahoo. com http: //cm. bell-labs. com/cm/cs/who/va va@agere. com mvatre@agere. com April 3, 2003 Agrawal: Fault Collapsing

Test Vector Generation Flow DUT Fault Model Generate fault list Collapse fault list Required fault coverage April 3, 2003 Generate test vectors Agrawal: Fault Collapsing

Background • Single stuck-at fault model is the most popularly used model. • Two faults f 1 and f 2 are equivalent if the same tests detect f 1 and f 2 (f 1=f 2) • If all tests of fault f 1 also detect fault f 2, then f 2 is said to dominate f 1 (f 1 f 2). a 0 a 1 b 0 b 1 April 3, 2003 c 0 c 1 a 0 = b 0 = c 0 : Equivalence a 1 c 1 b 1 c 1 : Dominance Agrawal: Fault Collapsing

Background • Both equivalence and dominance relations are transitive in nature. [ (f 1 f 2) and (f 2 f 3) => (f 1 f 3) ] • If f 1 dominates f 2 and f 2 dominates f 1 then f 1 and f 2 are equivalent. [ (f 1 f 2) and (f 2 f 1) => (f 1 = f 2) ] • Number of faults in a 2 -input AND gate reduces from 6 to 4 (by equivalence) and to 3 (by dominance) collapsing. Example: c 6288, #faults =12576 #equ. = 7744 (0. 62), #dom. = 5824 (0. 46) April 3, 2003 Agrawal: Fault Collapsing

Problem Statement • To devise a new method for fault collapsing with following attributes: – A single procedure for equivalence and dominance – Global analysis (independence from direction, and other choices, in collapsing) – Use functional equivalences and dominances – Hierarchical fault collapsing (collapsing in large circuits using pre-collapsed sub networks) April 3, 2003 Agrawal: Fault Collapsing

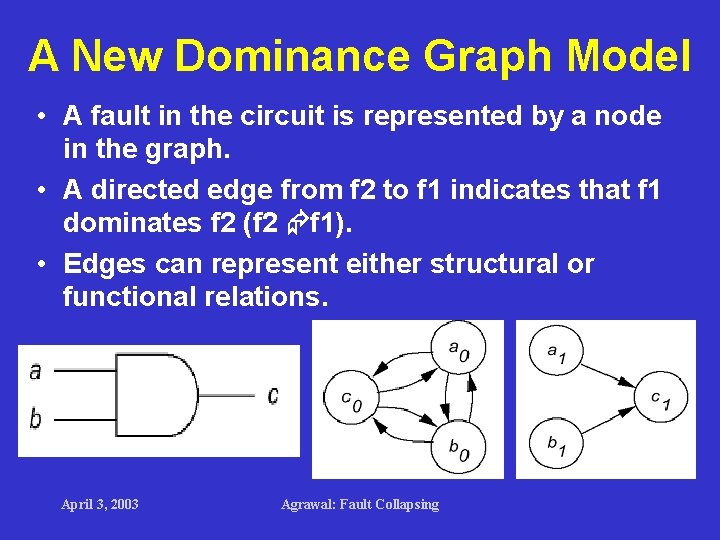
A New Dominance Graph Model • A fault in the circuit is represented by a node in the graph. • A directed edge from f 2 to f 1 indicates that f 1 dominates f 2 (f 2 f 1). • Edges can represent either structural or functional relations. April 3, 2003 Agrawal: Fault Collapsing

Computational Model • Graph is represented as a connectivity matrix • Each fault is assumed to be equivalent to itself • Treats functional and structural relations identically • (f 1 f 2) and (f 2 f 1) => f 2 = f 1. Appear as symmetrical components in the matrix (e. g. , a 0, b 0, c 0) • #faults = 6 (dimension of 2 -input AND gate dominance matrix) April 3, 2003 Agrawal: Fault Collapsing

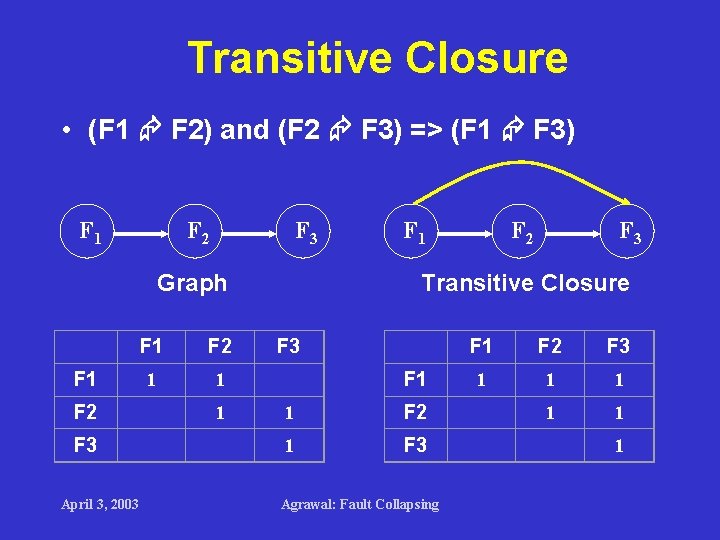
Transitive Closure • Transitive closure (TC) of the dominance matrix gives all dominance relations between faults. • TC is computed by the O(n 3) Floyd. Warshall algorithm, where n is the dimension of the dominance matrix. April 3, 2003 Agrawal: Fault Collapsing

Transitive Closure • (F 1 F 2) and (F 2 F 3) => (F 1 F 3) F 1 F 2 F 3 F 1 Graph F 2 F 3 Transitive Closure F 1 F 2 F 3 F 1 1 1 1 F 2 1 1 F 3 1 April 3, 2003 Agrawal: Fault Collapsing

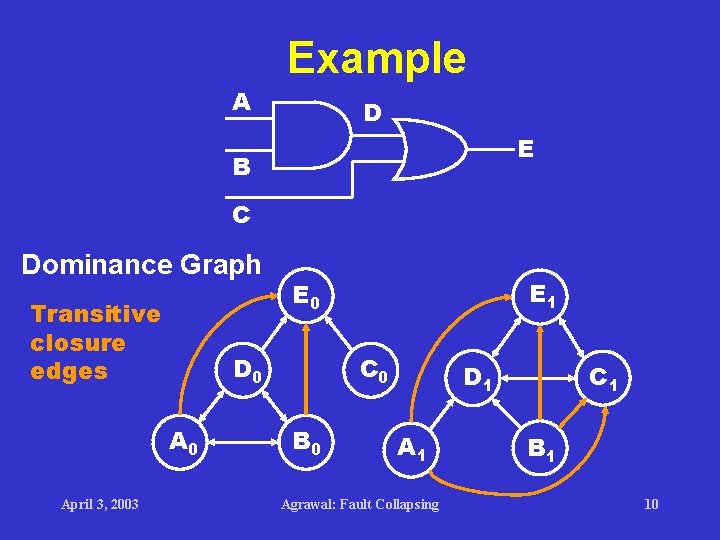
Example A D E B C Dominance Graph Transitive closure edges D 0 April 3, 2003 E 1 E 0 C 0 B 0 D 1 Agrawal: Fault Collapsing C 1 B 1 10

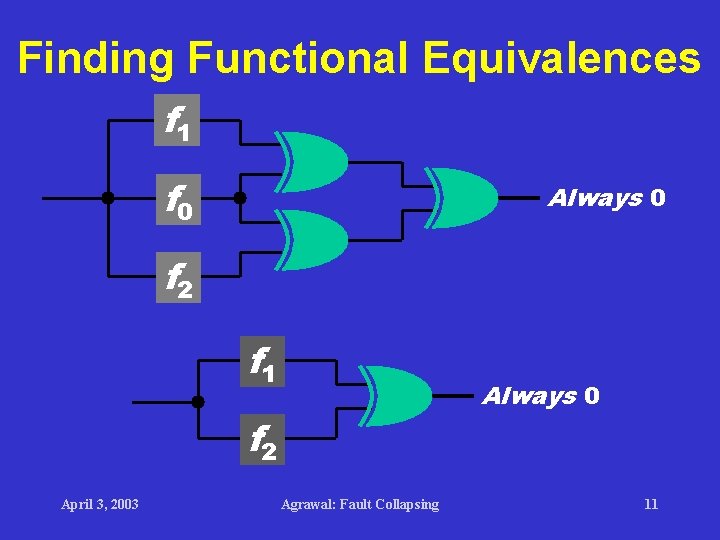
Finding Functional Equivalences f 1 f 0 Always 0 f 2 f 1 Always 0 f 2 April 3, 2003 Agrawal: Fault Collapsing 11

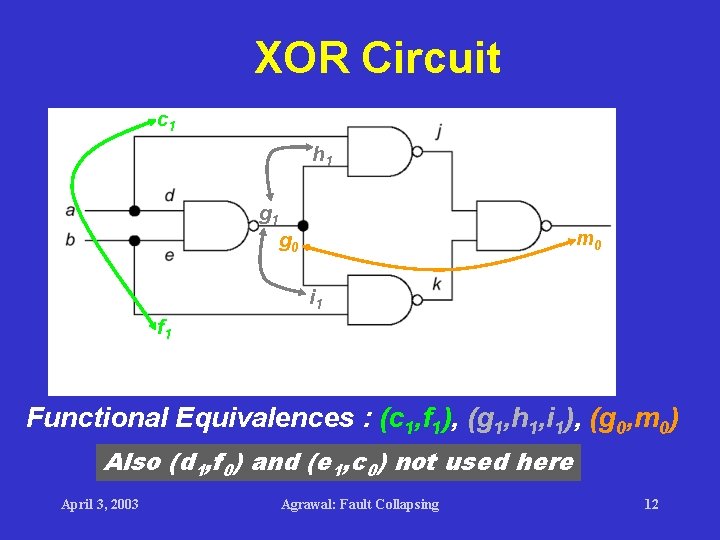
XOR Circuit c 1 h 1 g 1 m 0 g 0 i 1 f 1 Functional Equivalences : (c 1, f 1), (g 1, h 1, i 1), (g 0, m 0) Also (d 1, f 0) and (e 1, c 0) not used here April 3, 2003 Agrawal: Fault Collapsing 12

(24 x 24) Dominance matrix (XOR) Functional equivalences shown as boxed entries April 3, 2003 Agrawal: Fault Collapsing 13

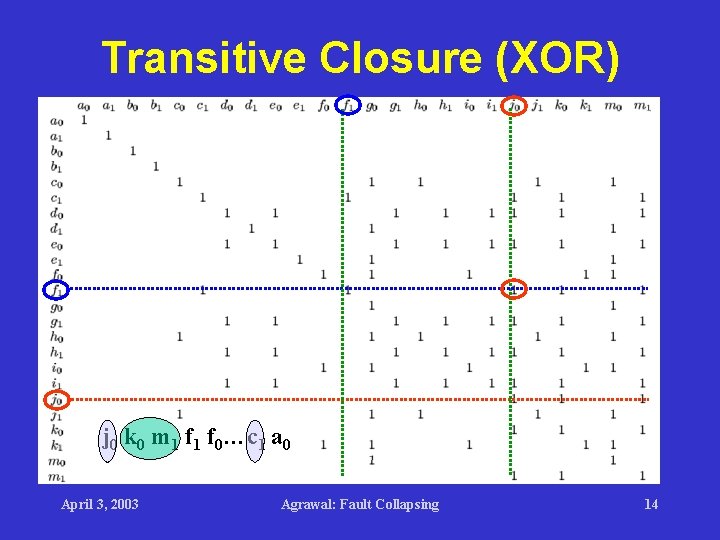
Transitive Closure (XOR) j 0 k 0 m 1 f 0…c 1 a 0 April 3, 2003 Agrawal: Fault Collapsing 14

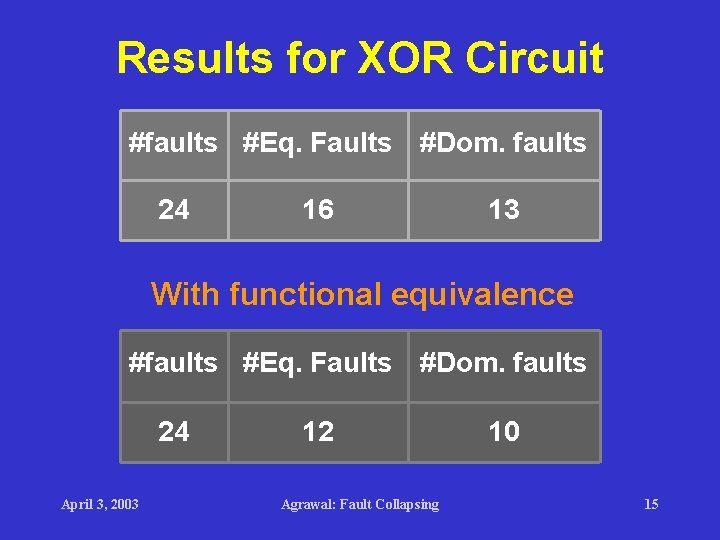
Results for XOR Circuit #faults #Eq. Faults #Dom. faults 24 16 13 With functional equivalence #faults #Eq. Faults #Dom. faults 24 April 3, 2003 12 Agrawal: Fault Collapsing 10 15

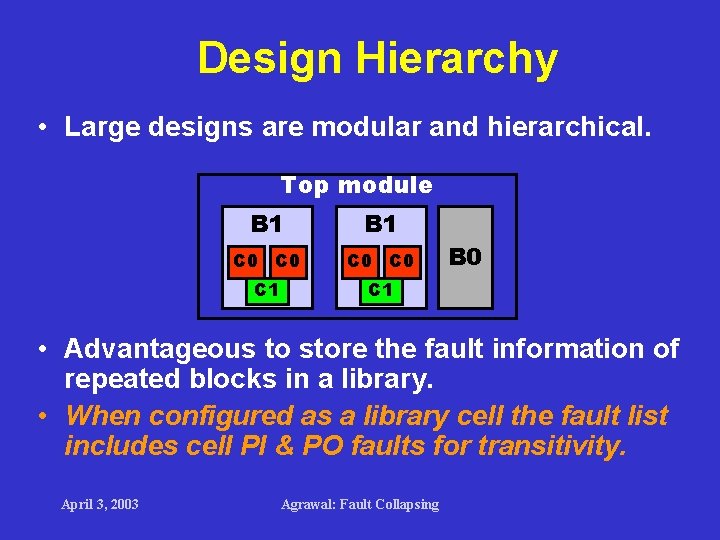
Design Hierarchy • Large designs are modular and hierarchical. Top module B 1 C 0 C 0 C 1 B 0 • Advantageous to store the fault information of repeated blocks in a library. • When configured as a library cell the fault list includes cell PI & PO faults for transitivity. April 3, 2003 Agrawal: Fault Collapsing

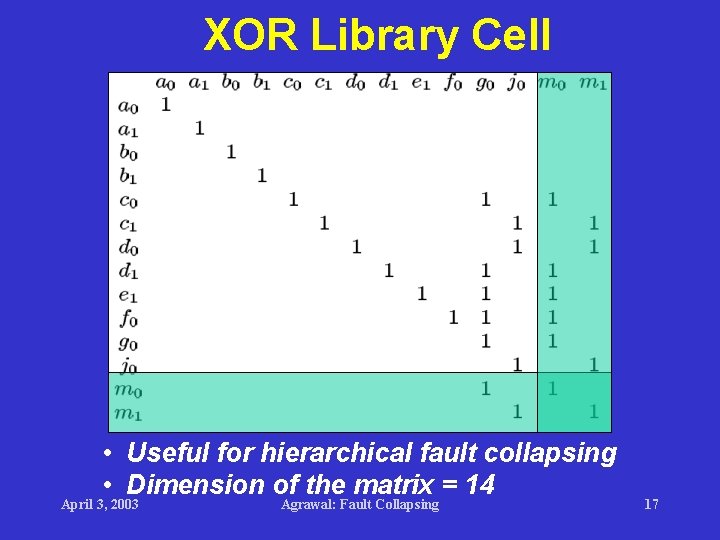
XOR Library Cell • Useful for hierarchical fault collapsing • Dimension of the matrix = 14 April 3, 2003 Agrawal: Fault Collapsing 17

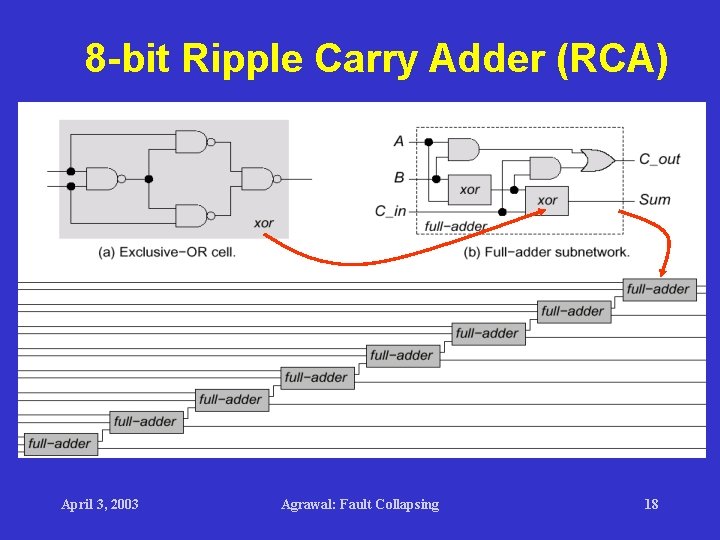
8 -bit Ripple Carry Adder (RCA) April 3, 2003 Agrawal: Fault Collapsing 18

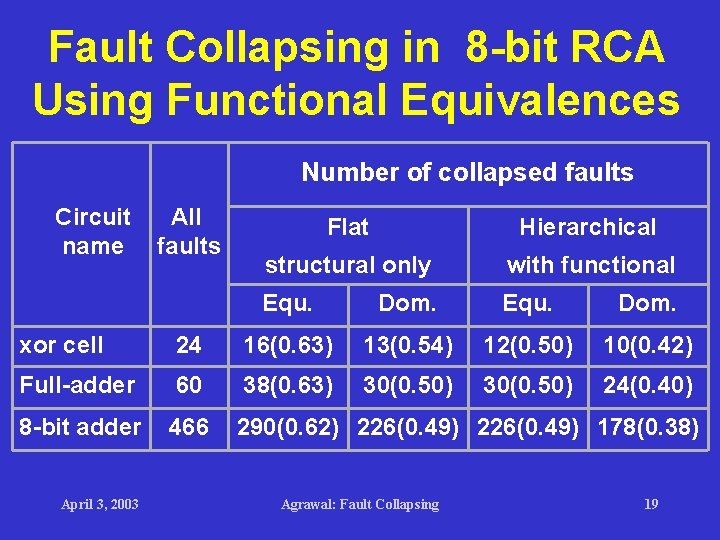
Fault Collapsing in 8 -bit RCA Using Functional Equivalences Number of collapsed faults Circuit name All faults Flat Hierarchical structural only with functional Equ. Dom. xor cell 24 16(0. 63) 13(0. 54) 12(0. 50) 10(0. 42) Full-adder 60 38(0. 63) 30(0. 50) 24(0. 40) 8 -bit adder 466 290(0. 62) 226(0. 49) 178(0. 38) April 3, 2003 Agrawal: Fault Collapsing 19

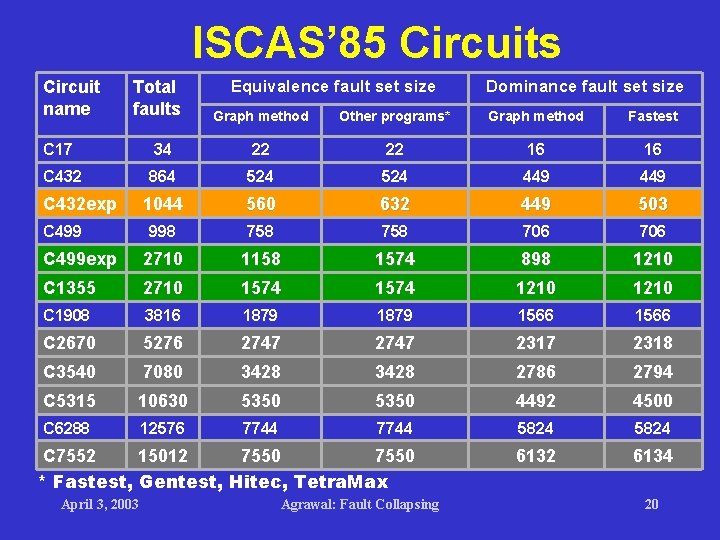
ISCAS’ 85 Circuits Circuit name Total faults Equivalence fault set size Dominance fault set size Graph method Other programs* Graph method Fastest C 17 34 22 22 16 16 C 432 864 524 449 1044 560 632 449 503 998 758 706 C 499 exp 2710 1158 1574 898 1210 C 1355 2710 1574 1210 C 1908 3816 1879 1566 C 2670 5276 2747 2317 2318 C 3540 7080 3428 2786 2794 C 5315 10630 5350 4492 4500 C 6288 12576 7744 5824 C 7552 15012 7550 * Fastest, Gentest, Hitec, Tetra. Max 6132 6134 C 432 exp C 499 April 3, 2003 Agrawal: Fault Collapsing 20

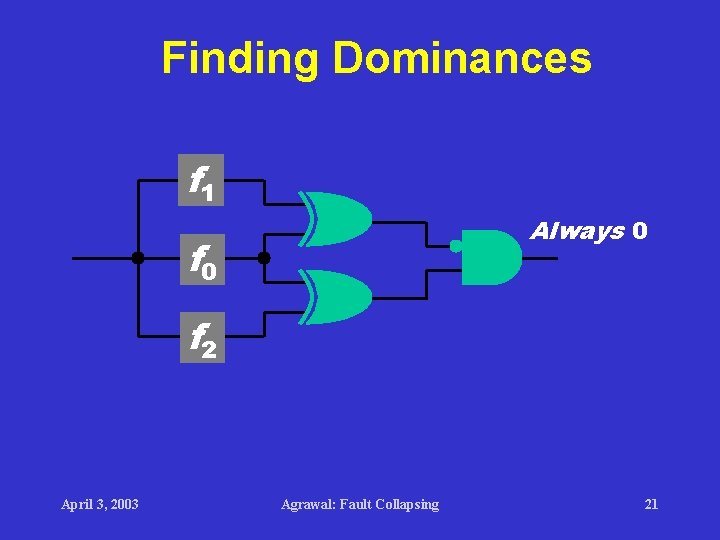
Finding Dominances f 1 Always 0 f 2 April 3, 2003 Agrawal: Fault Collapsing 21

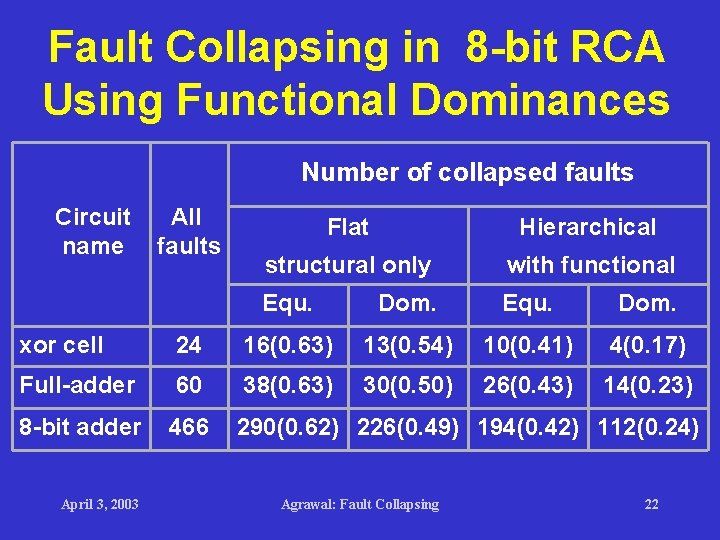
Fault Collapsing in 8 -bit RCA Using Functional Dominances Number of collapsed faults Circuit name All faults Flat Hierarchical structural only with functional Equ. Dom. xor cell 24 16(0. 63) 13(0. 54) 10(0. 41) 4(0. 17) Full-adder 60 38(0. 63) 30(0. 50) 26(0. 43) 14(0. 23) 8 -bit adder 466 290(0. 62) 226(0. 49) 194(0. 42) 112(0. 24) April 3, 2003 Agrawal: Fault Collapsing 22

Conclusion • A new algorithm for global fault collapsing • With functional equivalence number of faults for ATPG reduces considerably • Further reduction with functional dominances (Caution: fault coverage not correct when redundant faults are present) • Library based hierarchical fault collapsing is a new concept • Further studies are being carried out on independent fault sets • Reference: Prasad et al. , ITC-02, pp. 391 -397 April 3, 2003 Agrawal: Fault Collapsing