Hierarchical Fault Collapsing for Logic Circuits Masters Defense

Hierarchical Fault Collapsing for Logic Circuits Master’s Defense Raja K. K. R. Sandireddy Dept. of ECE, Auburn University Thesis Advisor: Vishwani D. Agrawal Committee Members: Victor P. Nelson, Charles E. Stroud Feb. 9, 2005 Raja Sandireddy: MS Defense Dept. of ECE, Auburn University

Outline • Introduction • Background – Fault Equivalence and Fault Dominance – Functional collapsing – Hierarchical fault collapsing • • • Fault Equivalence and Dominance definitions Algorithm to find dominance relations Results of functional collapsing Hierarchical fault collapsing Results of hierarchical fault collapsing Conclusions and Future work Feb. 9, 2005 Raja Sandireddy: MS Defense 2

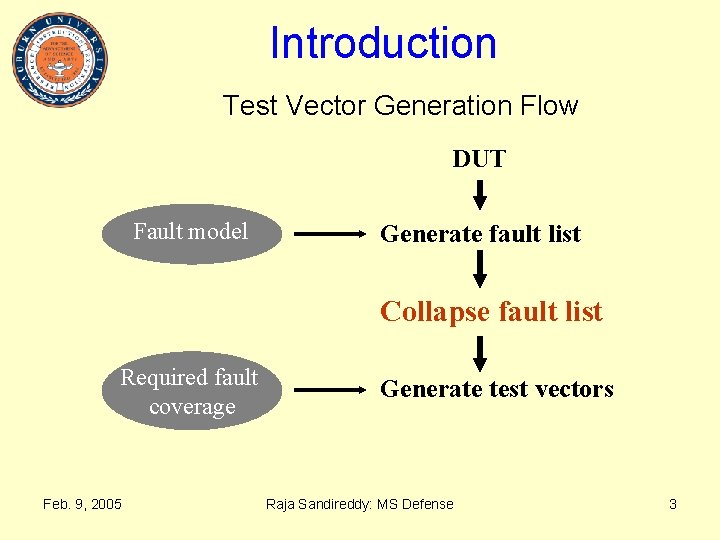
Introduction Test Vector Generation Flow DUT Fault model Generate fault list Collapse fault list Required fault coverage Feb. 9, 2005 Generate test vectors Raja Sandireddy: MS Defense 3

Stuck-at Fault • Single stuck-at fault model is the most popular model. a 0 a a 1 c 0 c c 1 b 0 b b 1 • Subscript fault notation: a 0 means stuck-at-0 on line a. Feb. 9, 2005 Raja Sandireddy: MS Defense 4

Equivalence Structural R-equivalence 1: Two faults f 1 and f 2 are said to be R-equivalent if they produce the same reduced circuit graph [netlist] when faulty values are implied and constant edges [signals] are removed. Functional F-equivalence 1: Two faults f 1 and f 2 are said to be F-equivalent if they modify the Boolean function of the circuit in the same way, i. e. , they yield the same output functions. E. J. Mc. Cluskey and F. W. Clegg, “Fault Equivalence in Combinational Logic Networks, ” IEEE Trans. Computers, vol. C-20, no. 11, Nov. 1971, pp. 1286 -1293. 1 Feb. 9, 2005 Raja Sandireddy: MS Defense 5

Structural Equivalence a 0 a 1 c 0 c 1 a 1 ≡ b 1 ≡ c 1 : Equivalence b 0 b 1 Equivalent faults are indistinguishable at all primary outputs of the circuit. Feb. 9, 2005 Raja Sandireddy: MS Defense 6

Structural Dominance A fault fi is said to dominate fault fj if the faults are equivalent with respect to test set of fault fj. a 0 a 1 c 0 c 1 b 0 b 1 Feb. 9, 2005 Dominance relations a 0 c 0 b 0 c 0 Equivalence Relations a 1 c 1 a 1 ≡ c 1 a 1 c 1 b 1 ≡ c 1 a 1 ≡ b 1 ≡ c 1 b 1 c 1 a 1 b 1 a 1 ≡ b 1 a 1 b 1 Raja Sandireddy: MS Defense } } 7

Fault Collapsing • Equivalence Collapsing: It is the process of selecting one fault from each equivalence fault set. • Dominance Collapsing: From the equivalence collapsed set, all the dominating faults are left out retaining their respective dominated faults. For the OR gate, Equivalence collapsed set = {a 0, b 0, c 1} Dominance collapsed set = {a 0, b 0, c 1} Feb. 9, 2005 Raja Sandireddy: MS Defense 8

Collapse Ratio Example: Full adder circuit. Total faults: 60 Structural equivalence collapsed set 2, 3 = 38 (0. 63) Structural dominance collapsed set 3 = 30 (0. 5) 2 Using Hitec: T. M. Niermann and J. H. Patel, “HITEC: A Test Generation Package for Sequential Circuits, ” Proc. European Design Automation Conference, Feb. 1991, pp. 214 -218. 3 Using Fastest: T. P. Kelsey, K. K. Saluja, and S. Y. Lee, “An Efficient Algorithm for Sequential Circuit Test Generation, ” IEEE Trans. Computers, vol. 42, no. 11, pp. 1361 -1371, Nov. 1993. Feb. 9, 2005 Raja Sandireddy: MS Defense 9

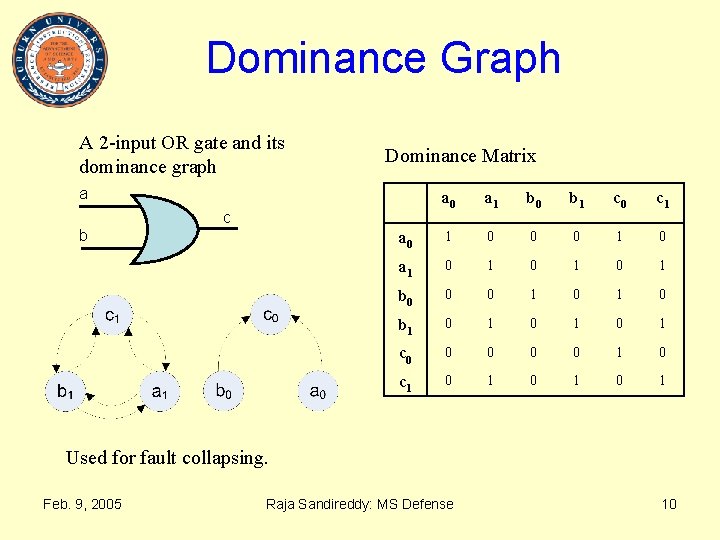
Dominance Graph A 2 -input OR gate and its dominance graph Dominance Matrix a a 0 a 1 b 0 b 1 c 0 c 1 a 0 1 0 0 0 1 0 a 1 0 1 0 1 b 0 0 0 1 0 b 1 0 1 0 1 c 0 0 0 1 0 c 1 0 1 0 1 c b Used for fault collapsing. Feb. 9, 2005 Raja Sandireddy: MS Defense 10

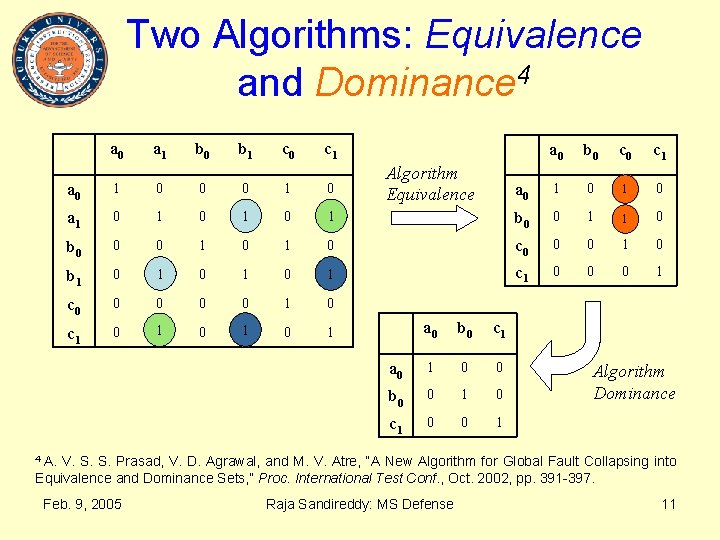
Two Algorithms: Equivalence and Dominance 4 a 0 a 1 b 0 b 1 c 0 c 1 Algorithm Equivalence a 0 b 0 c 1 a 0 1 0 0 0 1 0 a 1 0 1 0 1 b 0 0 1 11 0 b 0 0 0 1 0 c 0 0 0 1 0 b 1 0 1 0 1 c 1 0 0 0 1 c 0 0 0 1 0 c 1 0 1 0 1 a 0 b 0 c 1 a 0 1 0 0 b 0 0 1 0 c 1 0 0 1 Algorithm Dominance A. V. S. S. Prasad, V. D. Agrawal, and M. V. Atre, “A New Algorithm for Global Fault Collapsing into Equivalence and Dominance Sets, ” Proc. International Test Conf. , Oct. 2002, pp. 391 -397. 4 Feb. 9, 2005 Raja Sandireddy: MS Defense 11

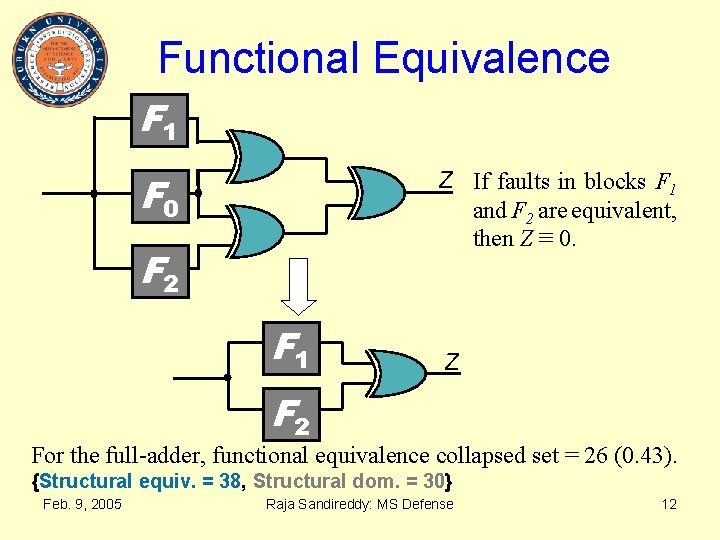
Functional Equivalence F 1 F 0 Z If faults in blocks F 1 and F 2 are equivalent, then Z ≡ 0. F 2 F 1 Z F 2 For the full-adder, functional equivalence collapsed set = 26 (0. 43). {Structural equiv. = 38, Structural dom. = 30} Feb. 9, 2005 Raja Sandireddy: MS Defense 12

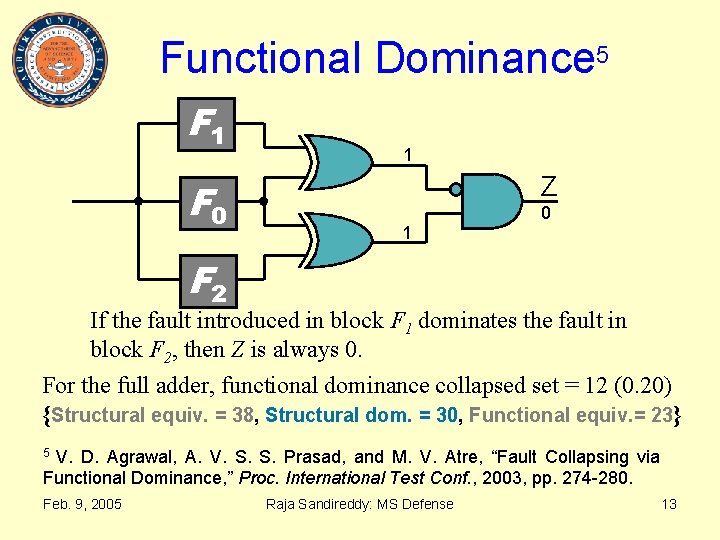
Functional Dominance 5 F 1 F 0 1 Z 1 0 F 2 If the fault introduced in block F 1 dominates the fault in block F 2, then Z is always 0. For the full adder, functional dominance collapsed set = 12 (0. 20) {Structural equiv. = 38, Structural dom. = 30, Functional equiv. = 23} V. D. Agrawal, A. V. S. S. Prasad, and M. V. Atre, “Fault Collapsing via Functional Dominance, ” Proc. International Test Conf. , 2003, pp. 274 -280. 5 Feb. 9, 2005 Raja Sandireddy: MS Defense 13

Hierarchical Circuits Increasing complexity of designs is efficiently handled by hierarchical design process. Hierarchical fault collapsing: • Create a library – For smaller sub-circuits, exhaustive collapsing is done using the methods discussed earlier. – For larger sub-circuits, use structural collapsing. • At the top level, do structural collapsing using the library information to collapse the faults at lower levels. Feb. 9, 2005 Raja Sandireddy: MS Defense 14

Hierarchical Fault Collapsing Advantages: • Fault set computed once is reused for all instances of the sub-circuit. • Exhaustive collapsing of faults in smaller circuits to achieve smaller collapsed sets. • Faster collapsing. Theorem 6: If two faults are functionally equivalent in a sub-circuit Ci that is embedded in a circuit Cj then they are also functionally equivalent in Cj. Note: Functional equivalence here means diagnostic equivalence as defined next. R. Hahn, R. Krieger, and B. Becker, “A Hierarchical Approach to Fault Collapsing, ” Proc. European Design & Test Conf. , 1994, pp. 171– 176. 6 Feb. 9, 2005 Raja Sandireddy: MS Defense 15

Equivalence Definitions • Fault Equivalence: Two faults are equivalent if and only if the corresponding faulty circuits have identical output functions. For multiple output circuits, this is extended for two possible interpretations. • Diagnostic Equivalence - Two faults of a Boolean circuit are called diagnostically equivalent if and only if the pair of the output functions is identical at each output of the circuit. • Detection Equivalence - Two faults are called detection equivalent if and only if all tests that detect one fault also detect the other fault, not necessarily at the same output. For single output circuits, diagnostic and detection equivalence mean the same. Diagnostic equivalence implies detection equivalence. Feb. 9, 2005 Raja Sandireddy: MS Defense 16

Examples to Demonstrate Detection Equivalence s-a-1 Q s-a-1 R The faults P 1, Q 1 and R 1 are detection equivalent faults, but not diagnostic equivalent. s-a-1 P A s-a-0 Y B c The faults c 0 and Y 0 are detection equivalent faults, but not diagnostic equivalent. Z s-a-0 For the full adder, diagnostic equivalence collapsed set = 26 (0. 43), detection equivalence collapsed set = 23 (0. 38) {Structural equiv. = 38, Structural dom. = 30, Functional equiv. = 26, Functional dom. = 12} Feb. 9, 2005 Raja Sandireddy: MS Defense 17

Dominance Definitions • Fault Dominance 7 - A fault fi is said to dominate fault fj if (a) the set of all vectors that detects fault fj is a subset of all vectors that detects fault fi and (b) each vector that detects fj implies identical values at the corresponding outputs of faulty versions of the circuit. Conventionally dominance is defined as: • A fault fi is said to dominate fault fj if the faults are equivalent with respect to test set of fault fj. • If all tests of fault fj detect another fault fi, then fi is said to dominate fj. J. F. Poage, “Derivation of Optimum Tests to Detect Faults in Combinational Circuits", Proc. Symposium on Mathematical Theory of Automata, 1962, pp. 483 -528. 7 Feb. 9, 2005 Raja Sandireddy: MS Defense 18

Dominance Definitions Contd. For multiple output circuits, the two possible interpretations of dominance: • Diagnostic dominance - If all tests of a fault f 1 detect another fault f 2 on the exact same outputs where f 1 was detected, then f 2 is said to diagnostically dominate f 1. • Detection dominance - If all tests of a fault f 1 detect another fault f 2, irrespective of the output where f 1 was detected, then f 2 is said to detection dominate f 1. Diagnostic dominance implies detection dominance. For the full adder, diagnostic dominance collapsed set = 12 (0. 2) detection dominance collapsed set = 6 (0. 1) {Structural equiv. = 38, Structural dom. = 30, Diagnostic equiv. = 26, Detection equiv. = 23} Feb. 9, 2005 Raja Sandireddy: MS Defense 19

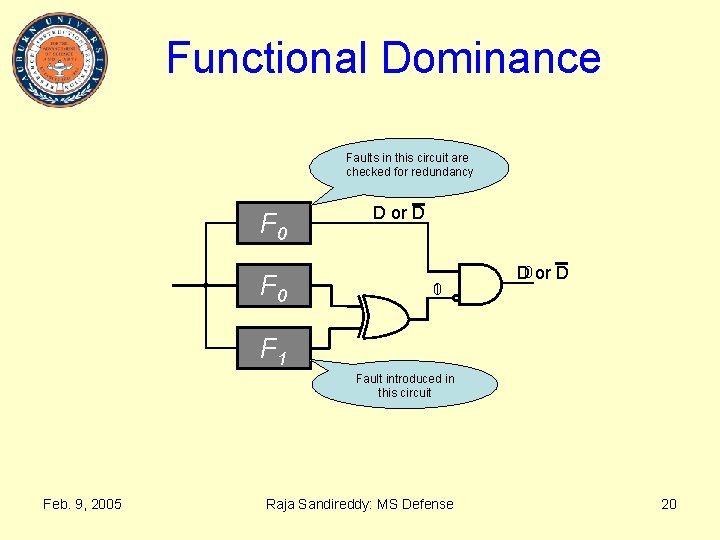
Functional Dominance Faults in this circuit are checked for redundancy F 0 D or D 10 D 0 or D F 1 Fault introduced in this circuit Feb. 9, 2005 Raja Sandireddy: MS Defense 20

Algorithm to Find All Dominance Relations 1. Select a fault from the given circuit and build the circuit as shown in previous slide with the fault introduced in the bottom block whose function is F 1. 2. Check for redundant faults in the top block, F 0. 3. For each redundant fault found in step 2, a 1 is placed in the dominance matrix at the intersection of the row corresponding to the redundant fault and the column corresponding to the fault in the bottom block. Thus, we obtain all values of a column of the dominance matrix in a single iteration. 4. Go to step 1 until there is no fault left. 5. Now we will have the dominance matrix with all the functional dominance relations included. Feb. 9, 2005 Raja Sandireddy: MS Defense 21

Algorithm Contd. 6. Transitive closure of the dominance matrix is computed, which is then reduced using algorithm equivalence 4. This reduced matrix still consists of dominance relations within an equivalence collapsed set of faults. 7. If dominance collapsing is required, then the reduced matrix of the previous step is further reduced according to algorithm dominance 4. For simplicity, the redundant faults of the given circuit (stand-alone F 0) are not considered in step 1. A. V. S. S. Prasad, V. D. Agrawal, and M. V. Atre, “A New Algorithm for Global Fault Collapsing into Equivalence and Dominance Sets, ” Proc. International Test Conf. , Oct. 2002, pp. 391 -397. 4 Feb. 9, 2005 Raja Sandireddy: MS Defense 22

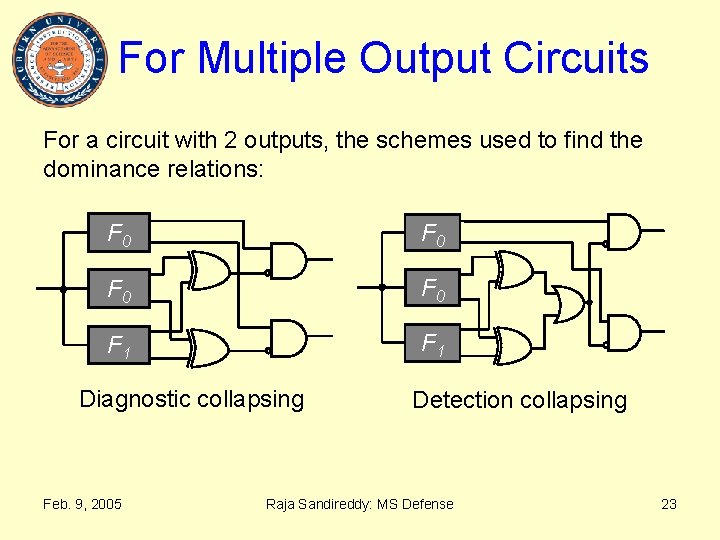
For Multiple Output Circuits For a circuit with 2 outputs, the schemes used to find the dominance relations: F 0 F 0 F 1 Diagnostic collapsing Feb. 9, 2005 Detection collapsing Raja Sandireddy: MS Defense 23

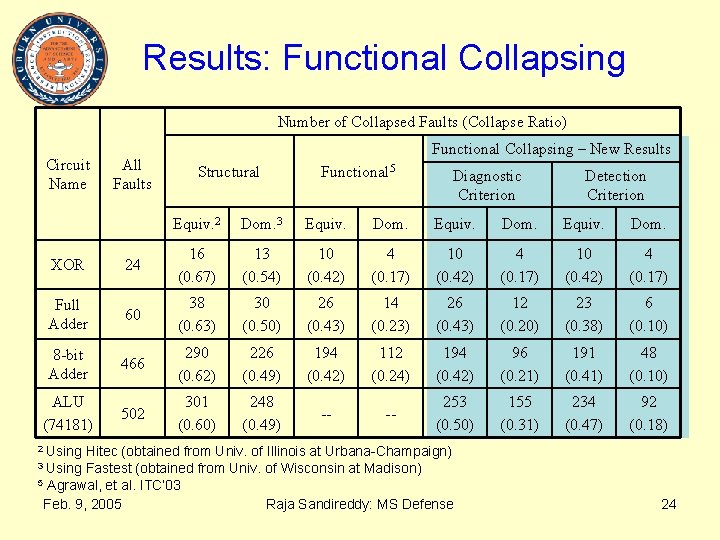
Results: Functional Collapsing Number of Collapsed Faults (Collapse Ratio) Circuit Name All Faults Functional Collapsing – New Results Structural Functional 5 Diagnostic Criterion Detection Criterion Equiv. 2 Dom. 3 Equiv. Dom. XOR 24 16 (0. 67) 13 (0. 54) 10 (0. 42) 4 (0. 17) Full Adder 60 38 (0. 63) 30 (0. 50) 26 (0. 43) 14 (0. 23) 26 (0. 43) 12 (0. 20) 23 (0. 38) 6 (0. 10) 8 -bit Adder 466 290 (0. 62) 226 (0. 49) 194 (0. 42) 112 (0. 24) 194 (0. 42) 96 (0. 21) 191 (0. 41) 48 (0. 10) ALU (74181) 502 301 (0. 60) 248 (0. 49) -- -- 253 (0. 50) 155 (0. 31) 234 (0. 47) 92 (0. 18) 2 Using Hitec (obtained from Univ. of Illinois at Urbana-Champaign) Fastest (obtained from Univ. of Wisconsin at Madison) 5 Agrawal, et al. ITC’ 03 Feb. 9, 2005 Raja Sandireddy: MS Defense 3 Using 24

Results: Test Vectors Test vectors obtained using Gentest ATPG 8. No. of test vectors (no. of target faults) Circuit Structural Functional – New Results Equivalence Dominance Diagnostic Dominance Detection Dominance Full Adder 6 (38) 6 (30) 7 (12) 6 (6) 8 -bit Adder 33 (290) 28 (226) 32 (96) 28 (48) ALU 44 (293) 44 (240) 39 (147) 38 (84) 8 W. T. Cheng and T. J. Chakraborty, “Gentest: An Automatic Test Generation System for Sequential Circuits, ” Computer, vol. 22, no. 4, pp. 43– 49, April 1989. Feb. 9, 2005 Raja Sandireddy: MS Defense 25

Hierarchical Fault Collapsing Line Oriented Structural Fault Collapsing 9: Type of gate the line feeds into Put this (these) fault (s) on the line INV, BUF None OR, NOR s-a-0 AND, NAND s-a-1 Sub-circuit, Fanout s-a-0, s-a-1 Primary Output s-a-0, s-a-1 M. Nadjarbashi, Z. Navabi, and M. R. Movahedin, “Line Oriented Structural Equivalence Fault Collapsing, “ IEEE Workshop on Model and Test, 2000. 9 Feb. 9, 2005 Raja Sandireddy: MS Defense 26

Hierarchical Fault Collapsing A G 1 01 0 1 B 0 0 M 1 G 2 G 3 G 4 0 1 1 0 C Algorithm to find the dominance matrix and its transitive closure: 1. Consider a fault (f 1) stuck-at-b at the input of a Boolean gate. 2. If the gate is of inverting type (NOT, NOR, NAND), then invert b. 3. If the equivalent set has s-a-b on this gate output, say f 2, then return this fault – place a 1 at the intersection of the row corresponding to f 1 and column corresponding to f 2 – use Update 10 for transitive closure. End. 4. Move one gate forward towards the primary output and go to step 2. K. K. Dave, V. D. Agrawal, and M. L. Bushnell, “Using Contrapositive Law in an Implication Graph to Identify Logic Redundancies, ” Proc. 18 th International Conf. VLSI Design, Jan. 2005, pp. 723 -729. 10 Feb. 9, 2005 Raja Sandireddy: MS Defense 27

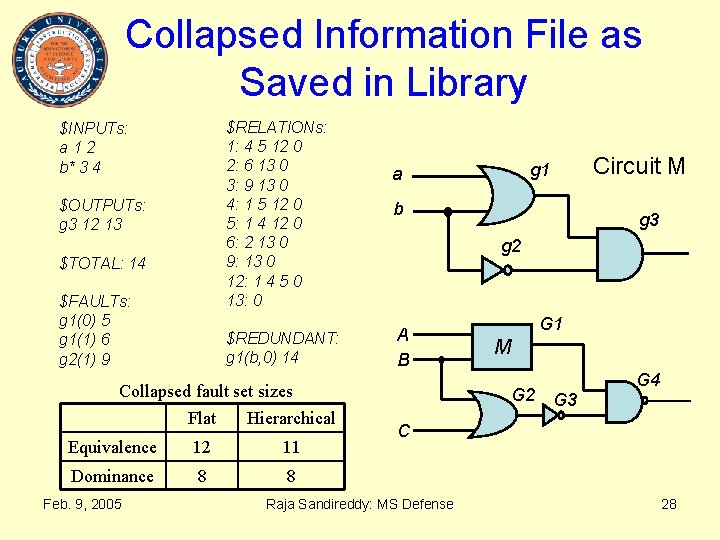
Collapsed Information File as Saved in Library $RELATIONs: 1: 4 5 12 0 2: 6 13 0 3: 9 13 0 4: 1 5 12 0 5: 1 4 12 0 6: 2 13 0 9: 13 0 12: 1 4 5 0 13: 0 $INPUTs: a 12 b* 3 4 $OUTPUTs: g 3 12 13 $TOTAL: 14 $FAULTs: g 1(0) 5 g 1(1) 6 g 2(1) 9 $REDUNDANT: g 1(b, 0) 14 Collapsed fault set sizes Flat Hierarchical Equivalence 12 11 Dominance 8 8 Feb. 9, 2005 g 1 a b Circuit M g 3 g 2 A B G 1 M G 2 G 3 G 4 C Raja Sandireddy: MS Defense 28

Results: Collapse Ratios Total Faults: Full adder: 60, 64 -bit Adder: 3714, 1024 -bit Adder: 59394, c 432: 1116, c 499: 2646 Detection collapsing can be used only for those sub-circuits whose outputs are POs at the top-level. Feb. 9, 2005 Raja Sandireddy: MS Defense 29

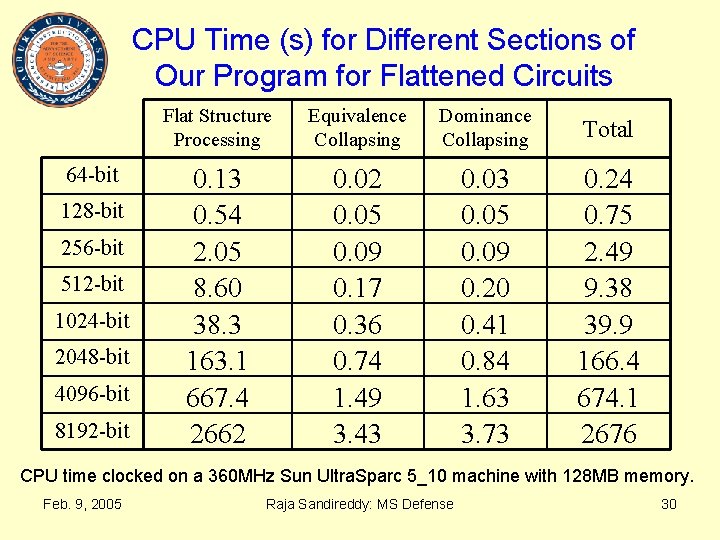
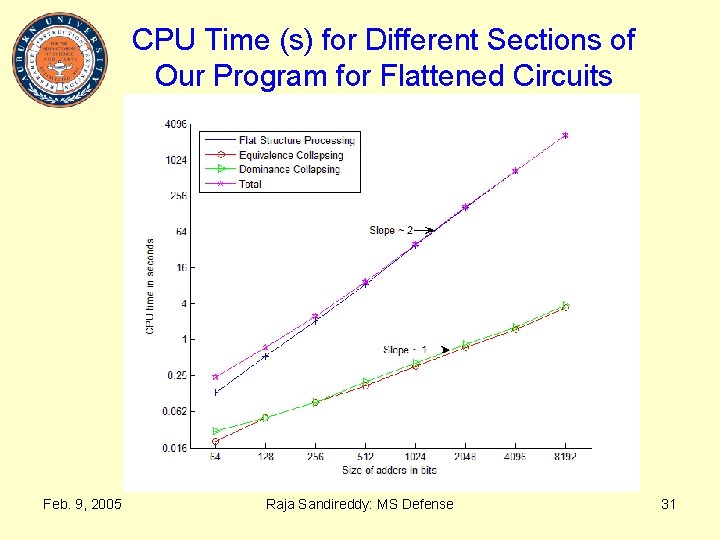
CPU Time (s) for Different Sections of Our Program for Flattened Circuits 64 -bit 128 -bit 256 -bit 512 -bit 1024 -bit 2048 -bit 4096 -bit 8192 -bit Flat Structure Processing Equivalence Collapsing Dominance Collapsing Total 0. 13 0. 54 2. 05 8. 60 38. 3 163. 1 667. 4 2662 0. 05 0. 09 0. 17 0. 36 0. 74 1. 49 3. 43 0. 05 0. 09 0. 20 0. 41 0. 84 1. 63 3. 73 0. 24 0. 75 2. 49 9. 38 39. 9 166. 4 674. 1 2676 CPU time clocked on a 360 MHz Sun Ultra. Sparc 5_10 machine with 128 MB memory. Feb. 9, 2005 Raja Sandireddy: MS Defense 30

CPU Time (s) for Different Sections of Our Program for Flattened Circuits Feb. 9, 2005 Raja Sandireddy: MS Defense 31

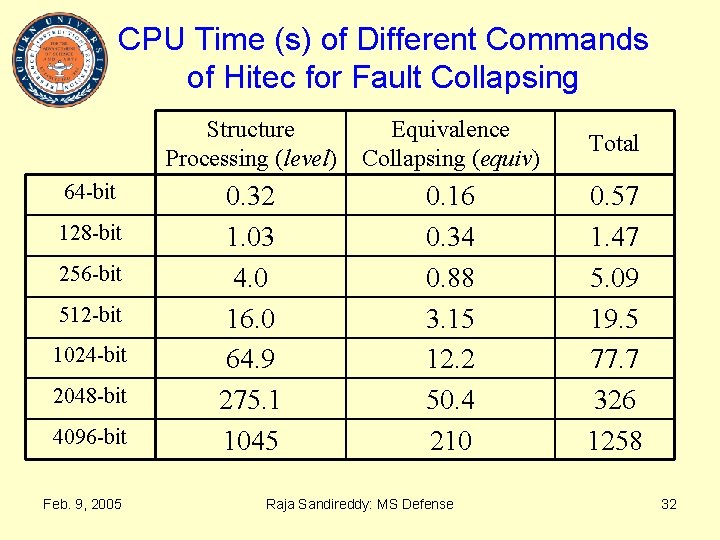
CPU Time (s) of Different Commands of Hitec for Fault Collapsing 64 -bit 128 -bit 256 -bit 512 -bit 1024 -bit 2048 -bit 4096 -bit Feb. 9, 2005 Structure Processing (level) Equivalence Collapsing (equiv) Total 0. 32 1. 03 4. 0 16. 0 64. 9 275. 1 1045 0. 16 0. 34 0. 88 3. 15 12. 2 50. 4 210 0. 57 1. 47 5. 09 19. 5 77. 7 326 1258 Raja Sandireddy: MS Defense 32

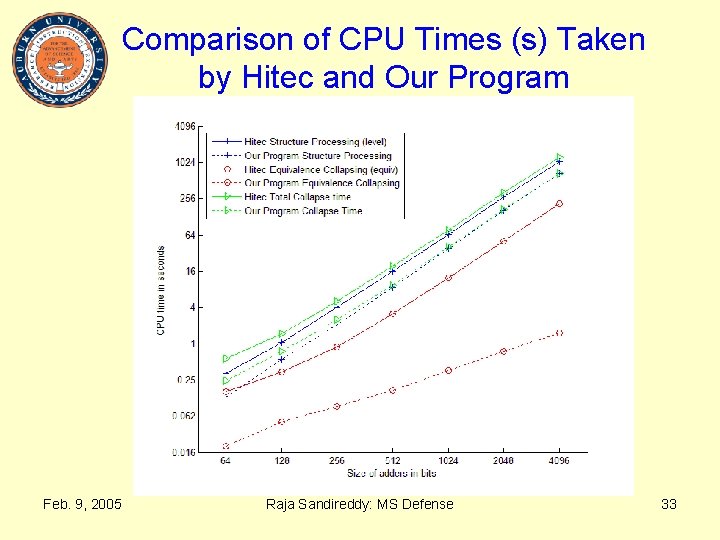
Comparison of CPU Times (s) Taken by Hitec and Our Program Feb. 9, 2005 Raja Sandireddy: MS Defense 33

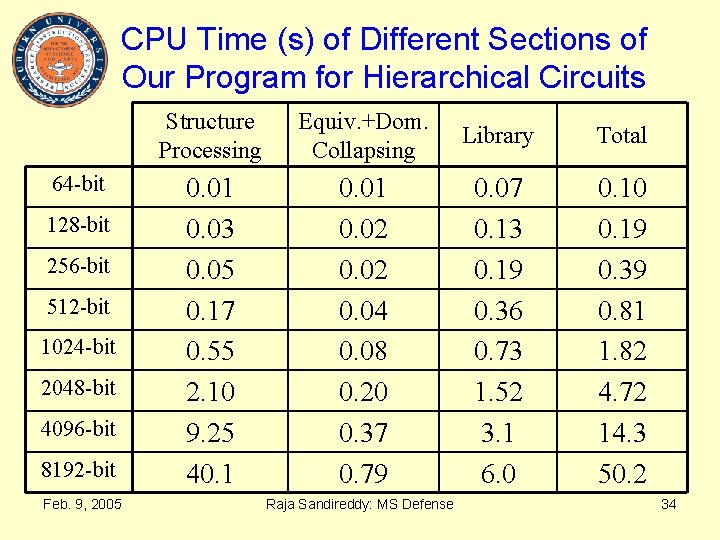
CPU Time (s) of Different Sections of Our Program for Hierarchical Circuits 64 -bit 128 -bit 256 -bit 512 -bit 1024 -bit 2048 -bit 4096 -bit 8192 -bit Feb. 9, 2005 Structure Processing Equiv. +Dom. Collapsing Library Total 0. 01 0. 03 0. 05 0. 17 0. 55 2. 10 9. 25 40. 1 0. 02 0. 04 0. 08 0. 20 0. 37 0. 79 0. 07 0. 13 0. 19 0. 36 0. 73 1. 52 3. 1 6. 0 0. 19 0. 39 0. 81 1. 82 4. 72 14. 3 50. 2 Raja Sandireddy: MS Defense 34

CPU Time (s) of Our Program for Hierarchical and Flattened Circuits Feb. 9, 2005 Raja Sandireddy: MS Defense 35

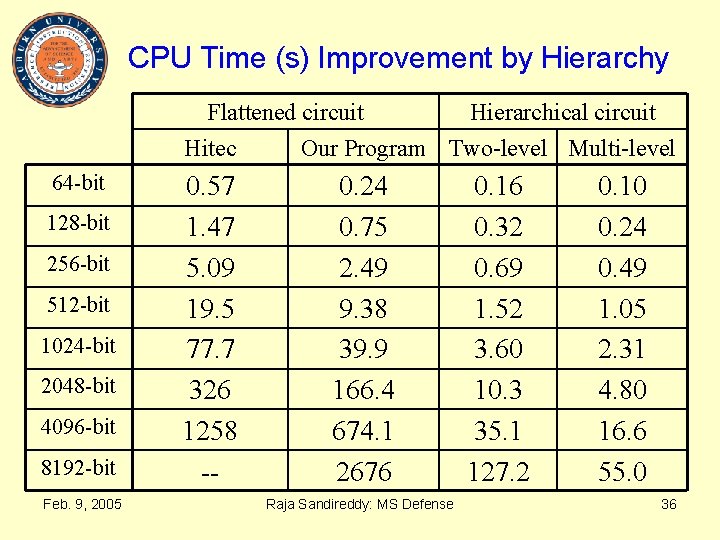
CPU Time (s) Improvement by Hierarchy Flattened circuit Hierarchical circuit Hitec Our Program Two-level Multi-level 64 -bit 128 -bit 256 -bit 512 -bit 1024 -bit 2048 -bit 4096 -bit 8192 -bit Feb. 9, 2005 0. 57 1. 47 5. 09 19. 5 77. 7 326 1258 -- 0. 24 0. 75 2. 49 9. 38 39. 9 166. 4 674. 1 2676 Raja Sandireddy: MS Defense 0. 16 0. 32 0. 69 1. 52 3. 60 10. 3 35. 1 127. 2 0. 10 0. 24 0. 49 1. 05 2. 31 4. 80 16. 6 55. 0 36

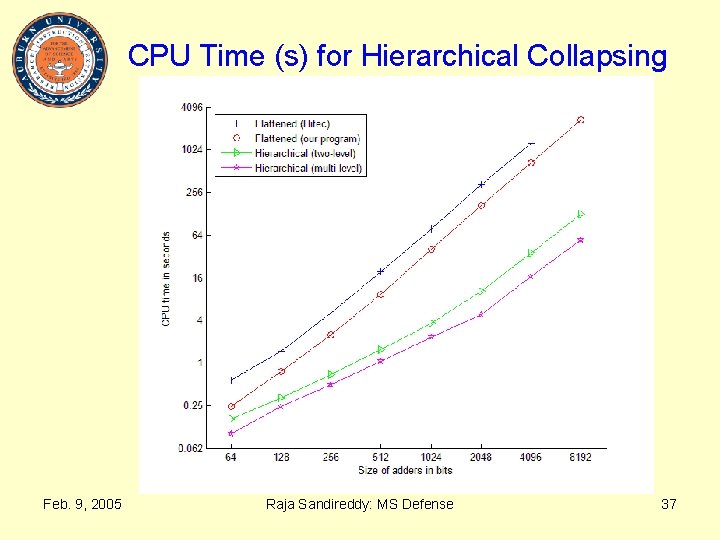
CPU Time (s) for Hierarchical Collapsing Feb. 9, 2005 Raja Sandireddy: MS Defense 37

Conclusions • Diagnostic and detection collapsing should be used only with smaller circuits. • Collapse ratios using detection dominance collapsing is about 10 -20%. • For larger circuits described hierarchically, use hierarchical fault collapsing. • Hierarchical fault collapsing: – Better (lower) collapse ratios due to functional collapsed library – Order of magnitude reduction in collapse time. 8192 -bit Adder • Smaller fault sets: – Fewer test vectors – Reduced fault simulation effort – Easier fault diagnosis. Dom. Collapsed Set Size (Collapse Ratio) CPU s Flat Hierarchical Flat Hier. 229378 (0. 48) 98304 (0. 21) 2676 55 • Use caution when using dominance collapsing!! Feb. 9, 2005 Raja Sandireddy: MS Defense 38

Future Work • Generate fault collapsing library of standard cells (Mentor Graphics, etc. ) • Incorporate VHDL or Verilog input for hierarchical netlist. • Efficient redundancy detection program. • Customized ATPG to obtain minimal test vector set. • Extend the work for sequential circuits. • Extend the work for other fault models. Feb. 9, 2005 Raja Sandireddy: MS Defense 39

THANK YOU Feb. 9, 2005 Raja Sandireddy: MS Defense 40