Hierarchical Bayesian Optimization Algorithm h BOA Martin Pelikan

Hierarchical Bayesian Optimization Algorithm (h. BOA) Martin Pelikan University of Missouri at St. Louis pelikan@cs. umsl. edu

Foreword l Motivation • • l Black-box optimization (BBO) problem • Set of all potential solutions • Performance measure (evaluation procedure) Task: Find optimum (best solution) Formulation useful: No need for gradient, numerical functions, … But many important and tough challenges This talk • • Combine machine learning and evolutionary computation Create practical and powerful optimizers (BOA and h. BOA) 2

Overview l l Black-box optimization (BBO) BBO via probabilistic modeling • Motivation and examples • Bayesian optimization algorithm (BOA) • Hierarchical BOA (h. BOA) Theory and experiment Conclusions 3

Black-box Optimization l l l Input • • How do potential solutions look like? How to evaluate quality of potential solutions? Output • Best solution (the optimum) Important • • • We don’t know what’s inside evaluation procedure Vector and tree representations common This talk: Binary strings of fixed length 4

BBO: Examples l l l Atomic cluster optimization • • Solutions: Vectors specifying positions of all atoms Performance: Lower energy is better Telecom network optimization • • Solutions: Connections between nodes (cities, …) Performance: Satisfy constraints, minimize cost Design • • Solutions: Vectors specifying parameters of the design Performance: Finite element analysis, experiment, … 5

BBO: Advantages & Difficulties l l Advantages • • Use same optimizer for all problems. No need for much prior knowledge. Difficulties • • Many places to go • • 100 -bit strings… 1267650600228229401496703205376 solutions. Enumeration is not an option. Many places to get stuck • Local operators are not an option. Must learn what’s in the box automatically. Noise, multiple objectives, interactive evaluation, . . . 6

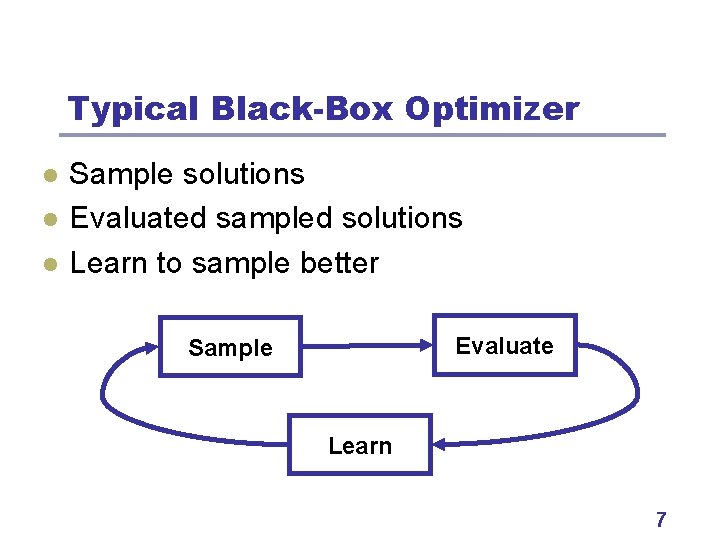
Typical Black-Box Optimizer l l l Sample solutions Evaluated sampled solutions Learn to sample better Evaluate Sample Learn 7

Many Ways to Do It l Hill climber l Simulated annealing l Evolutionary algorithms • Start with a random solution. • Flip bit that improves the solution most. • Finish when no more improvement possible. • Introduce Metropolis. • Inspiration from natural evolution and genetics. 8

Evolutionary Algorithms l l l Evolve a population of candidate solutions. Start with a random population. Iteration • Selection • • Select promising solutions Variation Apply crossover and mutation to selected solutions Replacement Incorporate new solutions into original population 9

Estimation of Distribution Algorithms l Replace standard variation operators by • Building a probabilistic model of promising • l solutions Sampling the built model to generate new solutions Probabilistic model • Stores features that make good solutions good • Generates new solutions with just those features 10

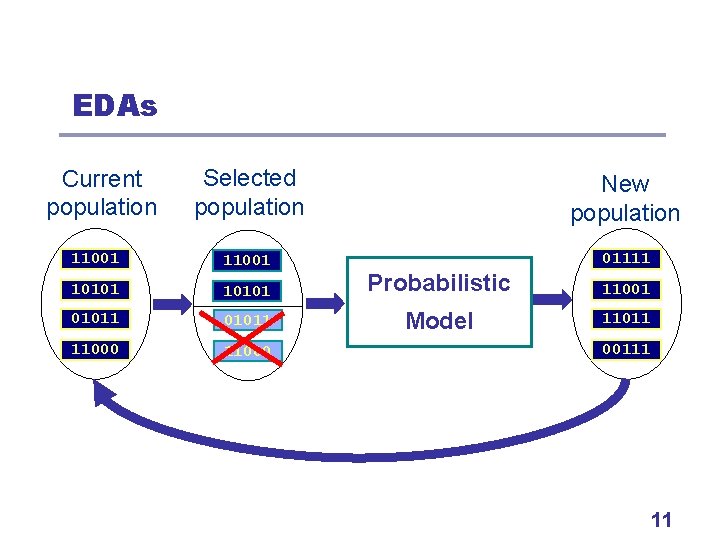
EDAs Selected population New population 11001 01111 10101 Probabilistic 11001 01011 Model 11011 11000 Current population 00111 11

What Models to Use? l Our plan • Simple example: Probability vector for binary strings • Bayesian networks (BOA) • Bayesian networks with local structures (h. BOA) 12

Probability Vector l l l Baluja (1995) Assumes binary strings of fixed length Stores probability of a 1 in each position. New strings generated with those proportions. Example: (0. 5, …, 0. 5) for uniform distribution (1, 1, …, 1) for generating strings of all 1 s 13

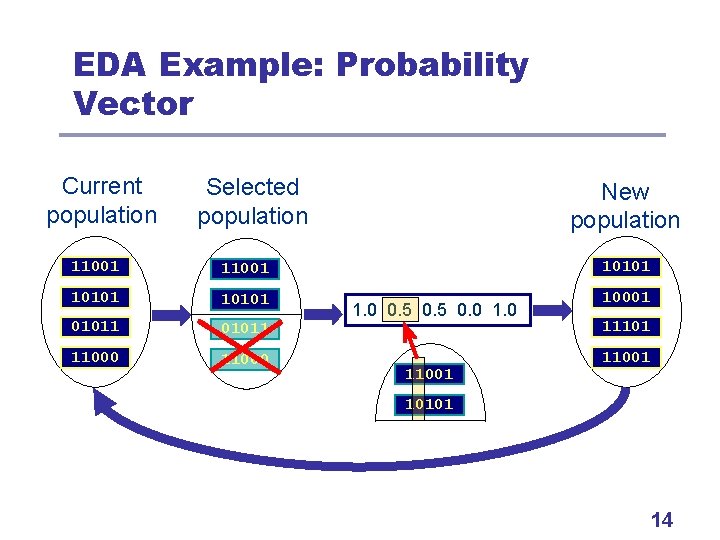
EDA Example: Probability Vector Current population Selected population New population 11001 10101 01011 11101 11000 11001 1. 0 0. 5 0. 0 11001 101011 11000 14

Probability Vector Dynamics l Bits that perform better get more copies. And are combined in new ways. But context of each bit is ignored. Example problem 1: ONEMAX l Optimum: 111… 1 l l l 15

Proportions of 1 s Probability Vector on ONEMAX Optimum Iteration 16

Proportions of 1 s Probability Vector on ONEMAX Optimum Success Iteration 17

Probability Vector: Ideal Scale-up l O(n log n) evaluations until convergence l Other algorithms • (Harik, Cantú-Paz, Goldberg, & Miller, 1997) • (Mühlenbein, Schlierkamp-Vosen, 1993) • Hill climber: O(n log n) (Mühlenbein, 1992) • GA with uniform: approx. O(n log n) • GA with one-point: slightly slower 18

When Does Prob. Vector Fail? l Example problem 2: Concatenated traps • Partition input string into disjoint groups of 5 bits. • Each group contributes via trap (ones=num. ones): • Concatenated trap = sum of single traps • Optimum: 111… 1 19

Trap Global optimum Number of 1 s 20

Proportions of 1 s Probability Vector on Traps Optimum Iteration 21

Proportions of 1 s Probability Vector on Traps Optimum Failure Iteration 22

Why Failure? l Onemax: • • Optimum in 111… 1 1 outperforms 0 on average. l Traps: optimum in 11111, but l So single bits are misleading. • f(0****) = 2 • f(1****) = 1. 375 23

How to Fix It? l l Consider 5 -bit statistics instead of 1 -bit ones. Then, 11111 would outperform 00000. Learn model • Compute p(00000), p(00001), …, p(11111) Sample model • • Sample 5 bits at a time Generate 00000 with p(00000), 00001 with p(00001), … 24

Proportions of 1 s Correct Model on Traps: Dynamics Optimum Iteration 25

Proportions of 1 s Correct Model on Traps: Dynamics Optimum Success Iteration 26

Good News: Good Stats Work Great! l l l Optimum in O(n log n) evaluations. Same performance as on onemax! Others • Hill climber: O(n 5 log n) = much worse. • GA with uniform: O(2 n) = intractable. • GA with one point: O(2 n) (without tight linkage). 27

Challenge l If we could learn and use context for each position • Find nonmisleading statistics. • Use those statistics as in probability vector. l Then we could solve problems decomposable into statistics of order at most k with at most O(n 2) evaluations! • And there are many of those problems. 28

Bayesian Optimization Algorithm (BOA) l l l Pelikan, Goldberg, & Cantú-Paz (1998) Use a Bayesian network (BN) as a model. Bayesian network • Acyclic directed graph. • Nodes are variables (string positions). • Conditional dependencies (edges). • Conditional independencies (implicit). 29

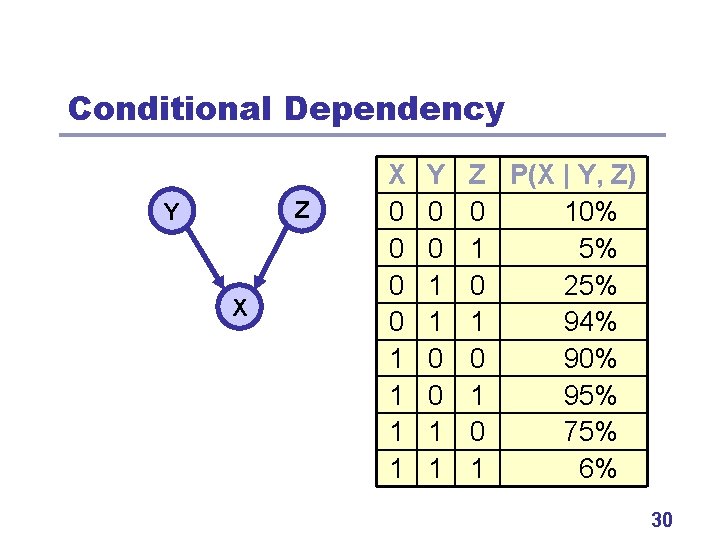
Conditional Dependency Z Y X X 0 0 1 1 Y 0 0 1 1 Z P(X | Y, Z) 0 10% 1 5% 0 25% 1 94% 0 90% 1 95% 0 75% 1 6% 30

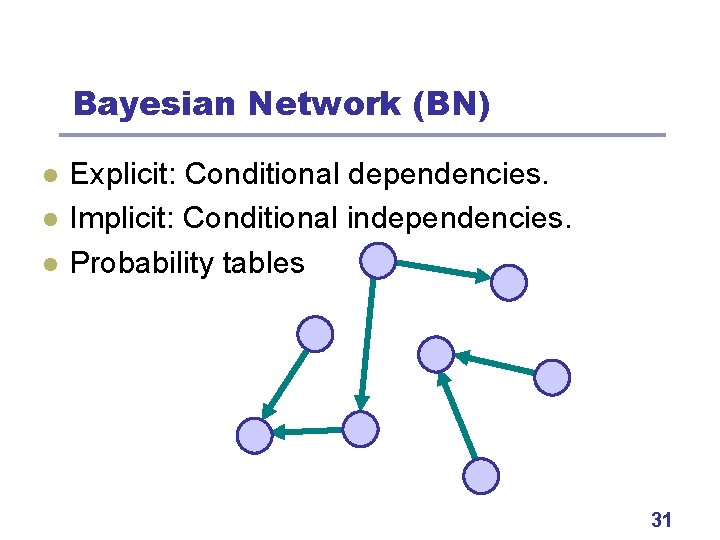
Bayesian Network (BN) l l l Explicit: Conditional dependencies. Implicit: Conditional independencies. Probability tables 31

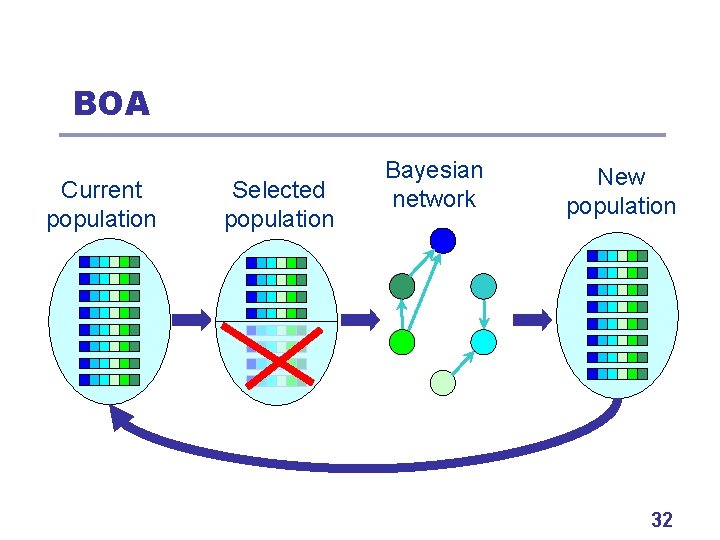
BOA Current population Selected population Bayesian network New population 32

BOA Variation l Two steps • Learn a Bayesian network (for promising solutions) • Sample the built Bayesian network (to generate new candidate solutions) l Next • Brief look at the two steps in BOA 33

Learning BNs l Two components: • Scoring metric (to evaluate models). • Search procedure (to find the best model). 34

Learning BNs: Scoring Metrics l l Bayesian metrics • Bayesian-Dirichlet with likelihood equivalence Minimum description length metrics • Bayesian information criterion (BIC) 35

Learning BNs: Search Procedure l l Start with an empty network (like prob. vec. ). Execute primitive operator that improves the metric the most. Until no more improvement possible. Primitive operators • Edge addition • Edge removal • Edge reversal. 36

Sampling BNs: PLS l l Probabilistic logic sampling (PLS) Two phases • Create ancestral ordering of variables: • Each variable depends only on predecessors Sample all variables in that order using CPTs: Repeat for each new candidate solution 37

BOA Theory: Key Components l l Primary target: Scalability Population sizing N • How large populations for reliable solution? Number of generations (iterations) G • How many iterations until convergence? Overall complexity • • O(N x G) Overhead: Low-order polynomial in N, G, and n. 38

BOA Theory: Population Sizing l l l Assumptions: n bits, subproblems of order k Initial supply (Goldberg) • Have enough partial sols. to combine. Decision making (Harik et al, 1997) • Decide well between competing partial sols. Drift (Thierens, Goldberg, Pereira, 1998) • Don’t lose less salient stuff prematurely. Model building (Pelikan et al. , 2000, 2002) • Find a good model. 39

BOA Theory: Num. of Generations l l l Two bounding cases Uniform scaling • • Subproblems converge in parallel Onemax model (Muehlenbein & Schlierkamp-Voosen, 1993) Exponential scaling • • Subproblems converge sequentially Domino convergence (Thierens, Goldberg, Pereira, 1998) 40

Good News l Theory • • Population sizing (Pelikan et al. , 2000, 2002) 1. 2. 3. 4. Initial supply. Decision making. Drift. Model building. Iterations until convergence (Pelikan et al. , 2000, 2002) 1. Uniform scaling. 2. Exponential scaling. l O(n) to O(n 1. 05) O(n 0. 5) to O(n) BOA solves order-k decomposable problems in O(n 1. 55) to O(n 2) evaluations! 41

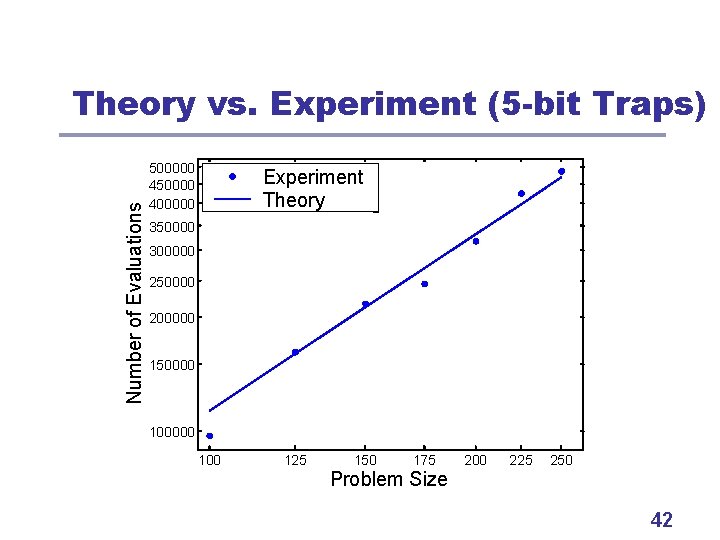
Number of Evaluations Theory vs. Experiment (5 -bit Traps) 500000 450000 400000 Experiment Theory 350000 300000 250000 200000 150000 100 125 150 175 Problem Size 200 225 250 42

Additional Plus: Prior Knowledge l BOA need not know much about problem l BOA can use prior knowledge • Only set of solutions + measure (BBO). • High-quality partial or full solutions. • Likely or known interactions. • Previously learned structures. • Problem specific heuristics, search methods. 43

From Single Level to Hierarchy l l l What if problem can’t be decomposed like this? Inspiration from human problem solving. Use hierarchical decomposition • Decompose problem on multiple levels. • Solutions from lower levels = basic building blocks • for constructing solutions on the current level. Bottom-up hierarchical problem solving. 44

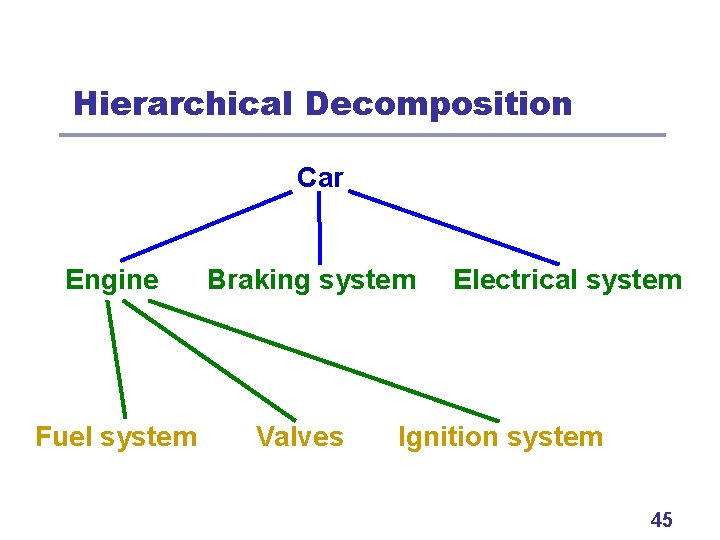
Hierarchical Decomposition Car Engine Fuel system Braking system Valves Electrical system Ignition system 45

3 Keys to Hierarchy Success l Proper decomposition l Chunking l Preservation of alternative solutions • Must decompose problem on each level properly. • Must represent & manipulate large order solutions. • Must preserve alternative partial solutions (chunks). 46

Hierarchical BOA (h. BOA) l Pelikan & Goldberg (2001) Proper decomposition l Chunking l Preservation of alternative solutions l • Use BNs as BOA. • Use local structures in BNs. • Restricted tournament replacement (niching). 47

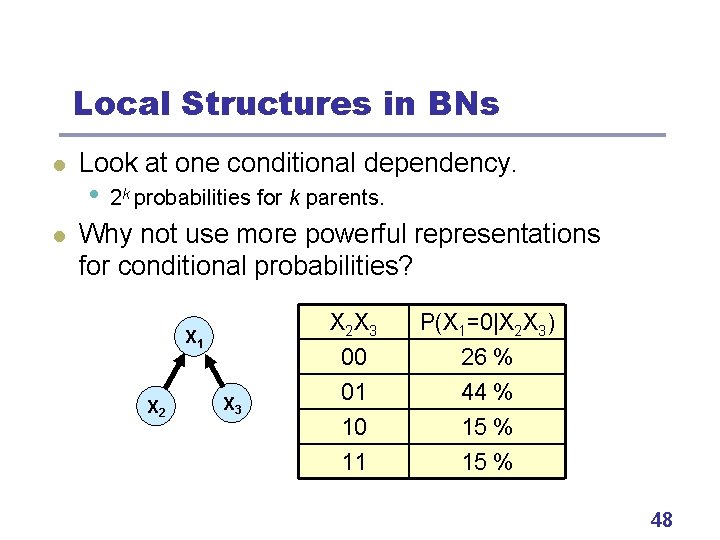
Local Structures in BNs l l Look at one conditional dependency. • 2 k probabilities for k parents. Why not use more powerful representations for conditional probabilities? X 1 X 2 X 3 X 2 X 3 P(X 1=0|X 2 X 3) 00 26 % 01 44 % 10 15 % 11 15 % 48

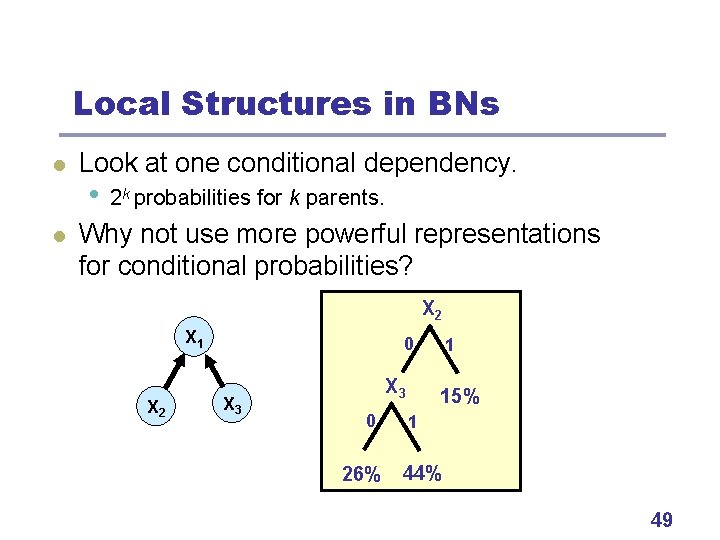
Local Structures in BNs l l Look at one conditional dependency. • 2 k probabilities for k parents. Why not use more powerful representations for conditional probabilities? X 2 X 1 X 2 0 X 3 0 26% 1 15% 1 44% 49

Restricted Tournament Replacement l l Used in h. BOA for niching. Insert each new candidate solution x like this: • Pick random subset of original population. • Find solution y most similar to x in the subset. • Replace y by x if x is better than y. 50

h. BOA: Scalability l l l Solves nearly decomposable and hierarchical problems (Simon, 1968) Number of evaluations grows as a low-order polynomial Most other methods fail to solve many such problems 51

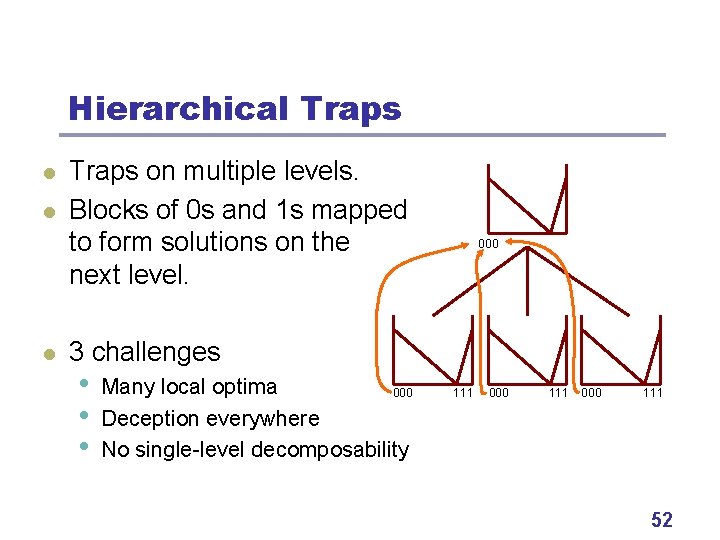
Hierarchical Traps l l l Traps on multiple levels. Blocks of 0 s and 1 s mapped to form solutions on the next level. 000 3 challenges • • • Many local optima 000 Deception everywhere No single-level decomposability 111 000 111 52

Hierarchical Traps 53

Other Similar Algorithms l l Estimation of distribution algorithms (EDAs) • Dynamic branch of evolutionary computation Examples: • • • PBIL (Baluja, 1995) • Univariate distributions (full independence) COMIT • Considers tree models ECGA • Groups of variables considered together EBNA (Etxeberria et al. , 1999), LFDA (Muhlenbein et al. , 1999) • Versions of BOA And others… 54

EDAs: Promising Results l l l l l Artificial classes of problems MAXSAT, SAT (Pelikan, 2005). Nurse scheduling (Li, Aickelin, 2003) Military antenna design (Santarelli et al. , 2004) Groundwater remediation design (Arst et al. , 2004) Forest management (Ducheyne et al. , 2003) Telecommunication network design (Rothlauf, 2002) Graph partitioning (Ocenasek, Schwarz, 1999; Muehlenbein, Mahnig, 2002; Baluja, 2004) Portfolio management (Lipinski, 2005) Quantum excitation chemistry (Sastry et al. , 2005) 55

Current Projects l l Algorithm design • • • h. BOA for computer programs. h. BOA for geometries (distance/angle-based). h. BOA for machine learners and data miners. h. BOA for scheduling and permutation problems. Efficiency enhancement for EDAs. Multiobjective EDAs. Applications • • • Cluster optimization and spin glasses. Data mining. Learning classifier systems & neural networks. 56

Conclusions for Researchers l Principled design of practical BBOers: l Facetwise design and little models • Scalability • Robustness • Solution to broad classes of problems • Useful for approaching research in evol. comp. • Allow creation of practical algorithms & theory 57

Conclusions for Practitioners l BOA and h. BOA revolutionary optimizers • Need no parameters to tune. • Need almost no problem specific knowledge. • But can incorporate knowledge in many forms. • Problem regularities discovered and exploited • • • automatically. Solves broad classes of challenging problems. Even problems unsolvable by any other BBOer. Can deal with noise & multiple objectives. 58

Book on h. BOA Martin Pelikan (2005) Hierarchical Bayesian optimization algorithm: Toward a new generation of evolutionary algorithms Springer 59

Contact Martin Pelikan Dept. of Math. and Computer Science, 320 CCB University of Missouri at St. Louis 8001 Natural Bridge Rd. St. Louis, MO 63121 pelikan@cs. umsl. edu http: //www. cs. umsl. edu/~pelikan/ 60

Problem 1: Concatenated Traps l l Partition input binary strings into 5 -bit groups. Partitions fixed but uknown. Each partition contributes the same. Contributions sum up. 61

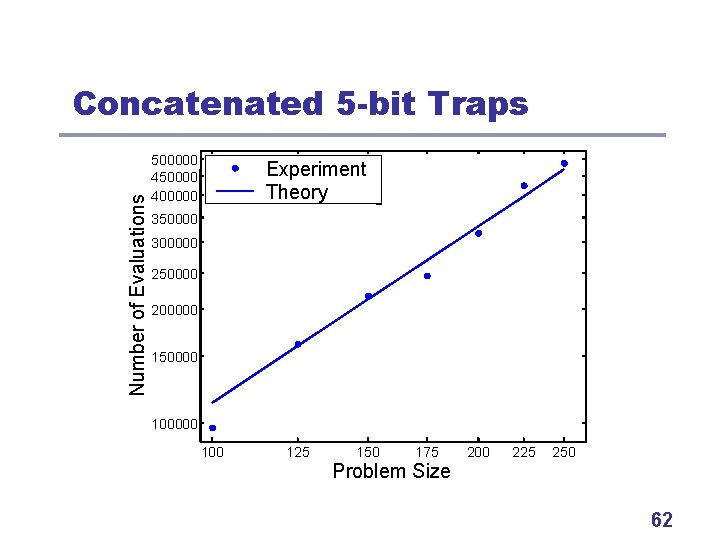
Number of Evaluations Concatenated 5 -bit Traps 500000 450000 400000 Experiment Theory 350000 300000 250000 200000 150000 100 125 150 175 Problem Size 200 225 250 62

Spin Glasses: Problem Definition l l l 1 D, 2 D, or 3 D grid of spins. Each spin can take values +1 or -1. Relationships between neighboring spins (i, j) are defined by coupling constants Ji, j. Usually periodic boundary conditions (toroid). Task: Find values of spins to minimize the energy 63

Spin Glasses as Constraint Satisfaction ≠ ≠ ≠ = = ≠ ≠ = Spins: Constraints: ≠ = ≠ ≠ 64

Spin Glasses: Problem Difficulty l l 1 D – Easy, set spins sequentially. 2 D – Several polynomial methods exist, best is • • l l Exponentially many local optima Standard approaches (e. g. simulated annealing, MCMC) fail 3 D – NP-complete, even for couplings {-1, 0, +1}. Often random subclasses are considered • • +-J spin glasses: Couplings uniform -1 or +1 Gaussian spin glasses: Couplings N(0, 2). 65

Ising Spin Glasses (2 D) 66

Results on 2 D Spin Glasses l l Number of evaluations is O(n 1. 51). Overall time is O(n 3. 51). Compare O(n 3. 51) to O(n 3. 5) for best method (Galluccio & Loebl, 1999) Great also on Gaussians. 67

Ising Spin Glasses (3 D) 68

MAXSAT l l Given a CNF formula. Find interpretation of Boolean variables that maximizes the number of satisfied clauses. (x 2 x 7 x 5 ) (x 1 x 4 x 3) 69

MAXSAT Difficulty l MAXSAT is NP complete for k-CNF, k>1 l But “random” problems are rather easy for almost any method. l Many interesting subclasses on SATLIB, e. g. • 3 -CNF from phase transition ( c = 4. 3 n ) • CNFs from other problems (graph coloring, …) 70

MAXSAT: Random 3 CNFs 71

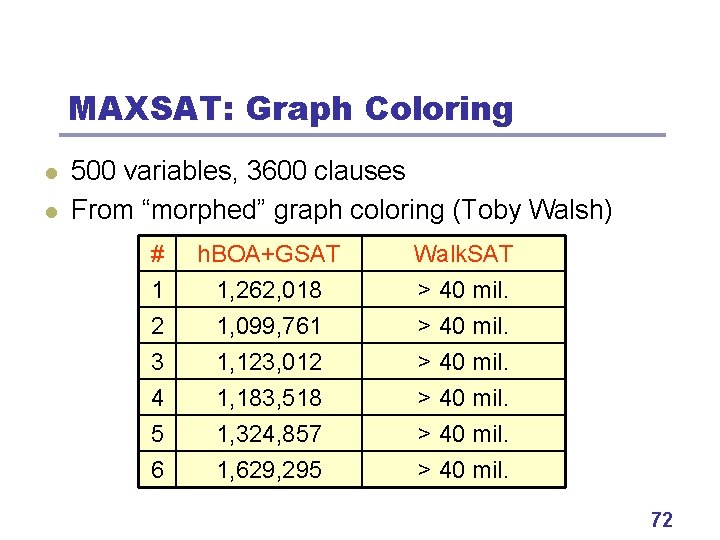
MAXSAT: Graph Coloring l l 500 variables, 3600 clauses From “morphed” graph coloring (Toby Walsh) # 1 2 3 h. BOA+GSAT 1, 262, 018 1, 099, 761 1, 123, 012 Walk. SAT > 40 mil. 4 5 6 1, 183, 518 1, 324, 857 1, 629, 295 > 40 mil. 72

Spin Glass to MAXSAT l Convert each coupling Jij with spins si and sj: Jij =+1 (si sj) ( si sj) l l l Jij = -1 (si sj) ( si sj) Consistent pairs of spins = 2 sat. clauses Inconsistent pairs of spins = 1 sat. clause MAXSAT solvers perform poorly even in 2 D! 73