Hiding a Secret Image in a Cover Image

Hiding a Secret Image in a Cover Image Chin-Chen Chang Computer Science and Information Engineering National Chung Cheng University July, 2004

Outline Introduction to image hiding Review some image hiding schemes LSB-based image hiding scheme VQ-based image hiding scheme Side-match oriented image hiding scheme Experiments and conclusions 2

Introduction to Image Hiding Secret key Hiding system Stego image Secret image Cover image 3

Cover Carriers Image Video Sound Text 4

Requirements Imperceptibility Embedding image should not appear any artificial effect Capacity Maximize the embedding payloads Security Secret messages can not be extracted by the illegal users 5

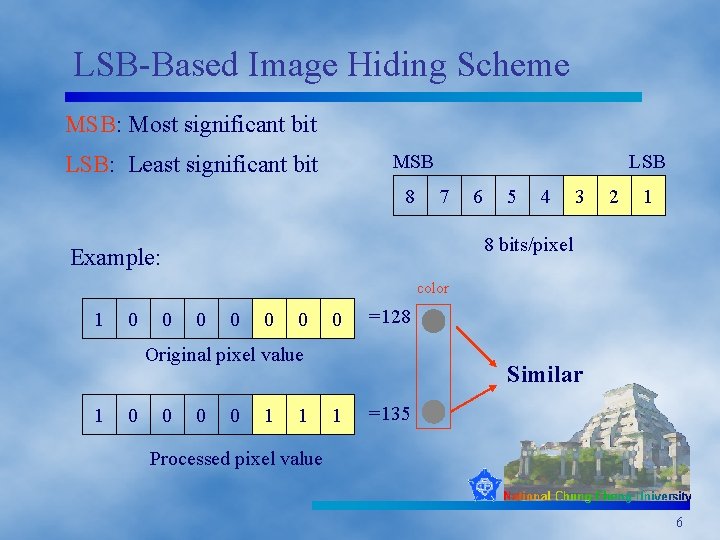
LSB-Based Image Hiding Scheme MSB: Most significant bit MSB LSB: Least significant bit 8 LSB 7 6 5 4 3 2 1 8 bits/pixel Example: color 1 0 0 0 0 =128 Original pixel value 1 0 0 1 1 Similar 1 =135 Processed pixel value 6

VQ-Based Image Hiding Scheme 7

Vector Quantization (VQ) VQ is a block-based lossy image compression method Definition of vector quantization (VQ): , where Y is a finite subset of Rk. VQ is composed of the following three parts: Codebook generation process, Encoding process, and Decoding process. 8

Standard VQ Compression W×H W H i (100, 125, …, 100) Original image index i i 31 19 254 12 13 1 74 41 67 24 123 7 2 60 24 56 85 45 23 15 85 150 14 45 12 71 83 200 66 Index table Codebook 9

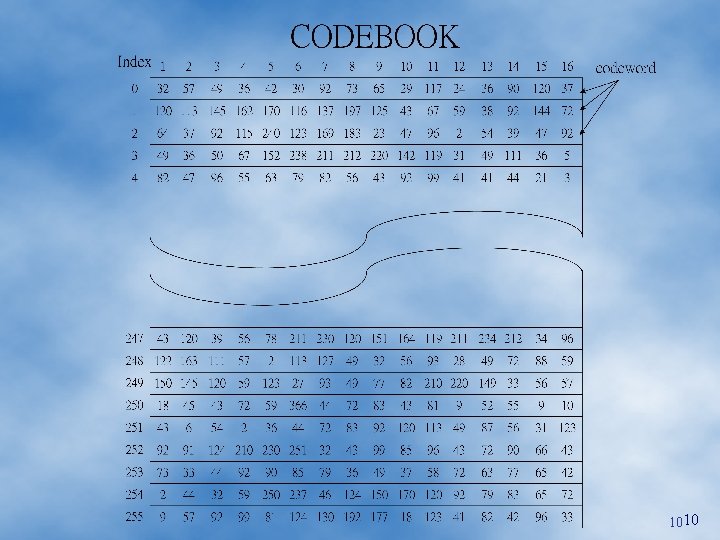
1010

VQ Codebook Training 0 1. . . N-1 Training Images Training set Separating the image to vectors 11

VQ Codebook Training 0 1. . . N-1 Training set 0 1. . . 254 255 Initial codebook Codebook initiation 12

Vector Quantization (VQ) Codebook Training 0 1. . . Index sets (1, 2, 5, 9, 45, …) (101, 179, 201, …) 0 1. . . (8, 27, 38, 19, 200, …) 254 255 N-1 N Training set (23, 0, 67, 198, 224, …) Codebook Ci Compute mean values Replace the old vectors 0 1. . 254. 255 New Codebook Ci+1 Training using iteration algorithm 1313

Example Codebook To encode an input vector, for example, v = (150, 145, 121, 130) (1) Compute the distance between v with all vectors in codebook d(v, cw 1) = 114. 2 d(v, cw 2) = 188. 3 d(v, cw 3) = 112. 3 d(v, cw 4) = 124. 6 d(v, cw 5) = 122. 3 d(v, cw 6) = 235. 1 d(v, cw 7) = 152. 5 d(v, cw 8) = 63. 2 (2) So, we choose cw 8 to replace the input vector v. 1414

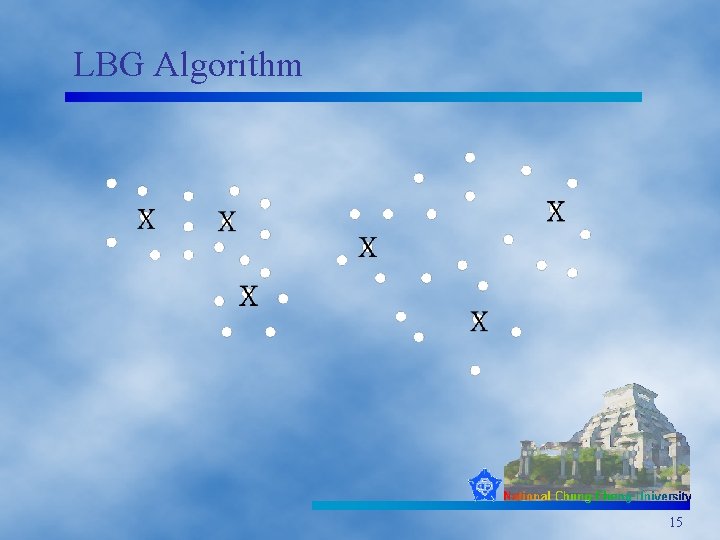
LBG Algorithm 15

Full Search (FS) For example: Let the codebook size be 256 Image vector # of searched nodes per image vector = 256 • Time consuming • The closest codeword C = {c 1, c 2, …, cnc} 1616

Euclidean Distance The dimensionality of vector = k (= w*h) An input vector x = (x 1, x 2, …, xk) A codeword yi = (yi 1, yi 2, …, yik) The Euclidean distance between x and yi 17

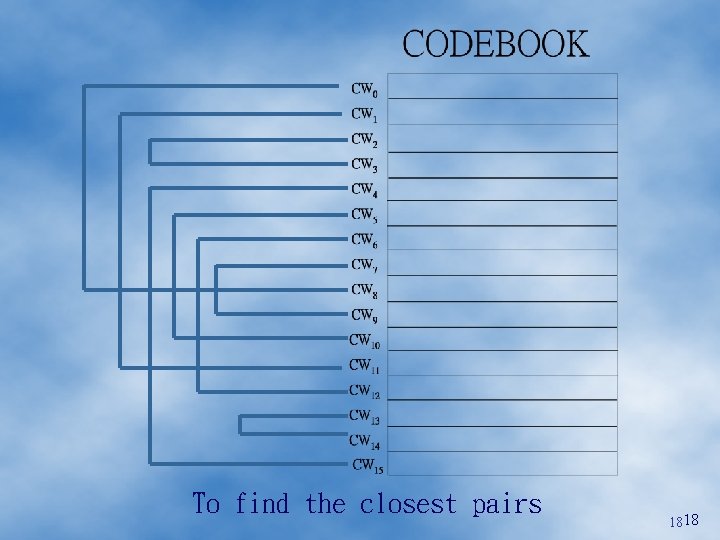
To find the closest pairs 1818

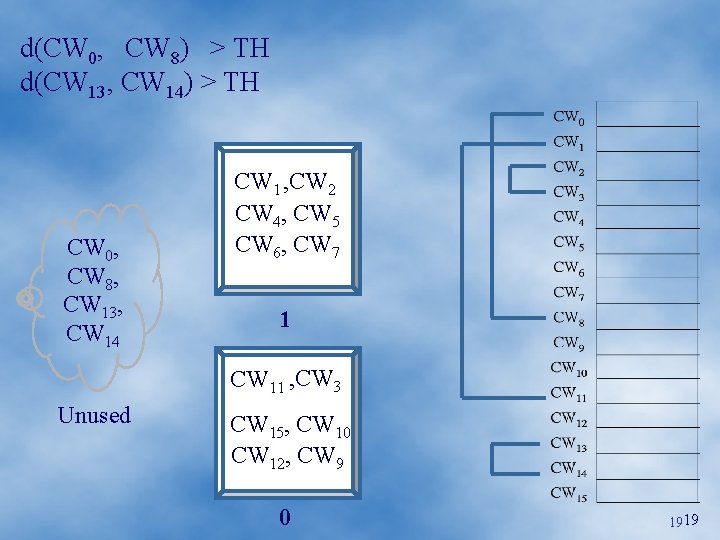
d(CW 0, CW 8) > TH d(CW 13, CW 14) > TH CW 0, CW 8, CW 13, CW 14 CW 1 , CW 2 CW 4, CW 5 CW 6, CW 7 1 CW 11 , CW 3 Unused CW 15, CW 10 CW 12, CW 9 0 1919

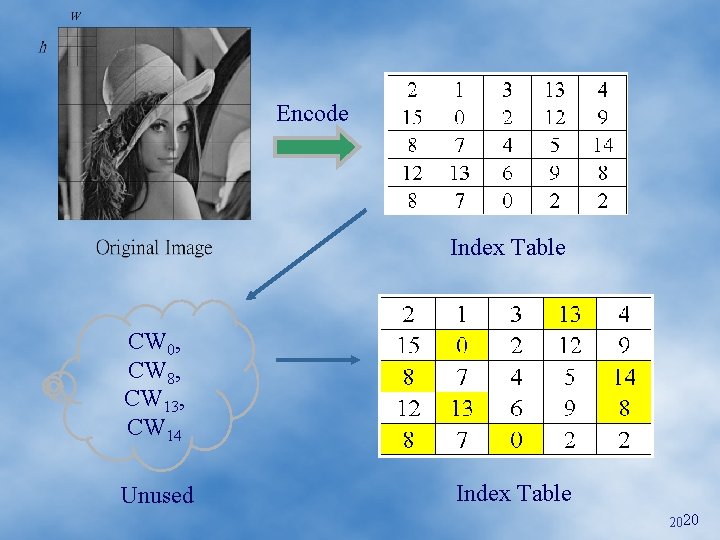
Encode Index Table CW 0, CW 8, CW 13, CW 14 Unused Index Table 2020

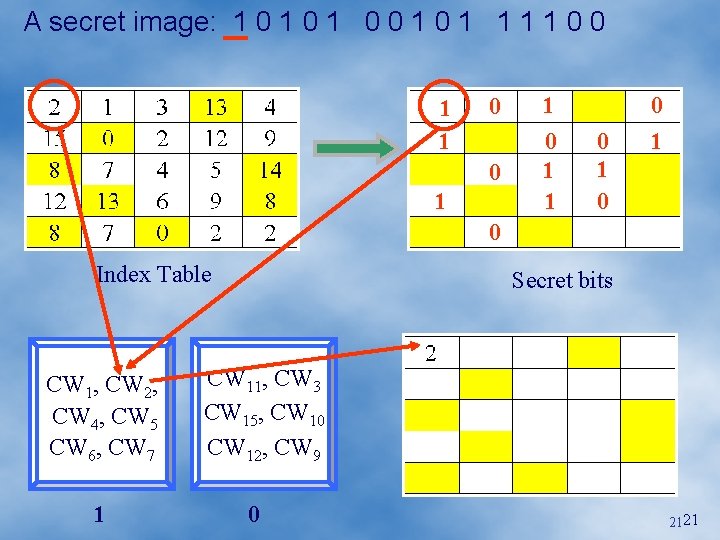
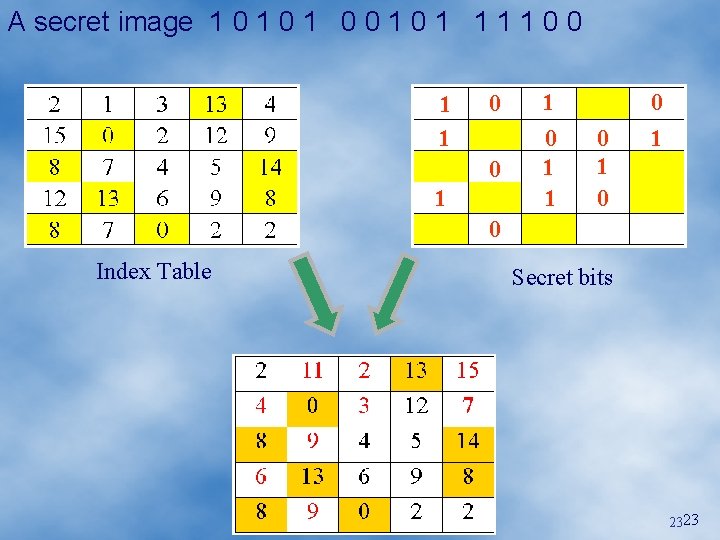
A secret image: 1 0 1 0 0 1 1 1 1 0 0 1 1 0 1 0 Index Table CW 1, CW 2, CW 4, CW 5 CW 6, CW 7 1 Secret bits CW 11, CW 3 CW 15, CW 10 CW 12, CW 9 0 2121

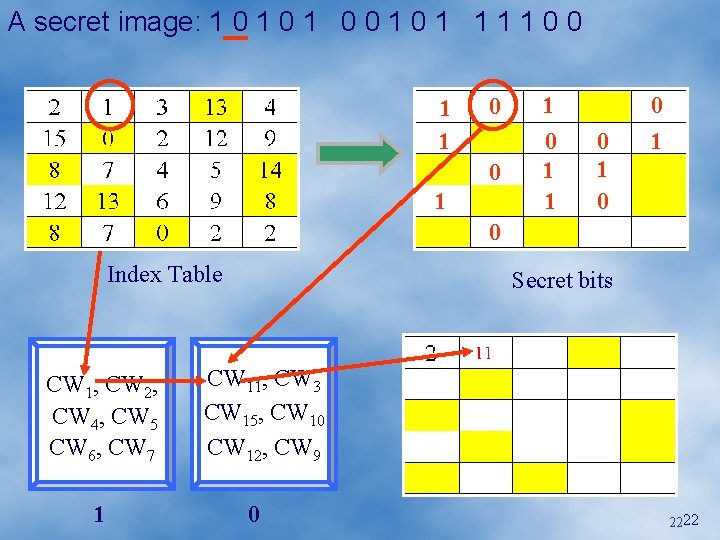
A secret image: 1 0 1 0 0 1 1 1 1 0 0 1 1 0 1 0 Index Table CW 1, CW 2, CW 4, CW 5 CW 6, CW 7 1 Secret bits CW 11, CW 3 CW 15, CW 10 CW 12, CW 9 0 2222

A secret image 1 0 1 0 0 1 1 1 1 0 0 1 1 0 1 0 Index Table Secret bits 2323

Side-match Oriented Image Hiding Scheme 24

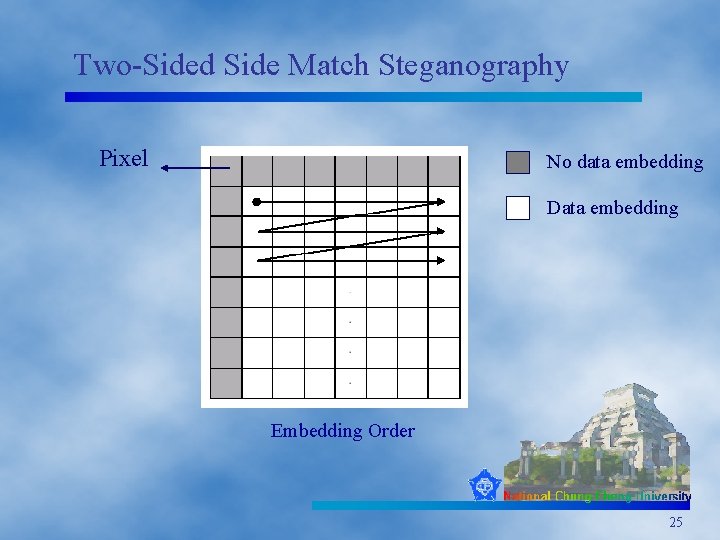
Two-Sided Side Match Steganography Pixel No data embedding Data embedding Embedding Order 25

Two-Sided Side Match Steganography (embedding) gu=82 gl=40 gx=47 gx: current pixel value d: difference value n: number of bits to be embedded b: embedded bits d': new difference value g'x: new pixel value d = (gu + gl)/2 – gx = (40+82)/2 – 47 = 14 n= log 2|14| =3 b = 1012 = 5 d' = 2 n+b = 23+5 = 13 g'x = (40+82)/2 – sign(14)*13 = 48 26

Two-Sided Side Match Steganography (extraction) gu=82 gl=40 gx=48 d = (gu + gl)/2 – gx = (40+82)/2 – 48 = 13 n = log 2|13| = 3 b = d – 2 n = 13 – 23 =5 = 1012 27

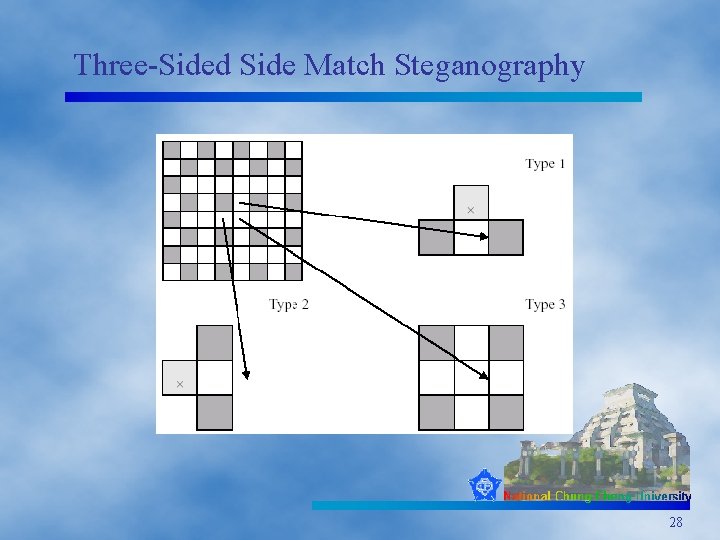
Three-Sided Side Match Steganography 28

Three-Sided Side Match Steganography (Type 1) gu=140 gl=150 gx=130 gr=130 Type 1: d = (gu + gl + gr)/3 – gx n = log 2| d | d' = 2 n+b g'x = (gu + gl + gr)/3 –Sign(d)* d' d = (140 +150 +130)/3 – 130=10 n = log 2| 10 | =3 d' = 2 n+b=23+5=13, b=1012=5 g'x = (140 +150 +130)/3 –Sign(10)*13=127 29

Three-Sided Side Match Steganography (Type 2) gu=150 gl=140 gx=130 gb=130 Type 2: d = (gu + gl + gb)/3 – gx n = log 2| d | d' = 2 n+b g'x = (gu + gl + gb)/3 – Sign(d)*d' d = (150 +140 +130)/3 – 130=10 n = log 2| 10 | =3 d' = 2 n+b=23+5=13, b=1012=5 g'x = (140 +150 +130)/3 –Sign(10)*13=127 30

Three-Sided Side Match Steganography (Type 3) g 4=150 g 1=160 gx=130 g 3=130 g 2=140 Type 3: d = (g 1 + g 2 + g 3 + g 4)/4 – gx n = log 2| d | d' = 2 n+b g'x = (g 1 + g 2 + g 3 + g 4)/4 -Sign(d)*d' d = (160 +140 +130+150)/4 – 130=15 n = log 2| 15 | =3 d' = 2 n+b=23+5=13, b=1012=5 g'x = (150 +130+140)/4 –Sign(15)*13=132 31

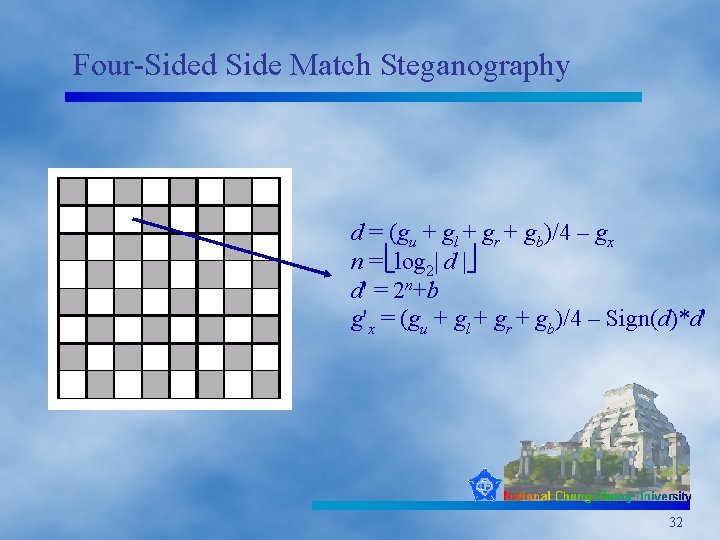
Four-Sided Side Match Steganography d = (gu + gl + gr + gb)/4 – gx n = log 2| d | d' = 2 n+b g'x = (gu + gl + gr + gb)/4 – Sign(d)*d' 32

Four-Sided Side Match Steganography Example gu=160 gl=150 gx=130 gr=140 gb=130 d = (gu + gl + gr + gb)/4 – gx n = log 2| d | d' = 2 n+b g'x = (gu + gl + gr + gb)/4 -Sign(d)*d' d = (160 +150 +140+130)/4 – 130=15 n = log 2| 15 | = 3 d' = 2 n+b=23+5=13, b=1012=5 g'x = (160 +150 +140+130)/4 –Sign(15)*13=132 33

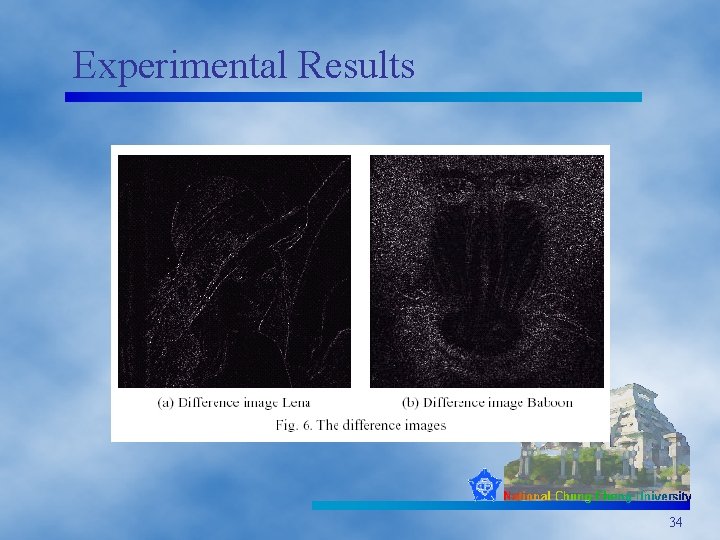
Experimental Results 34

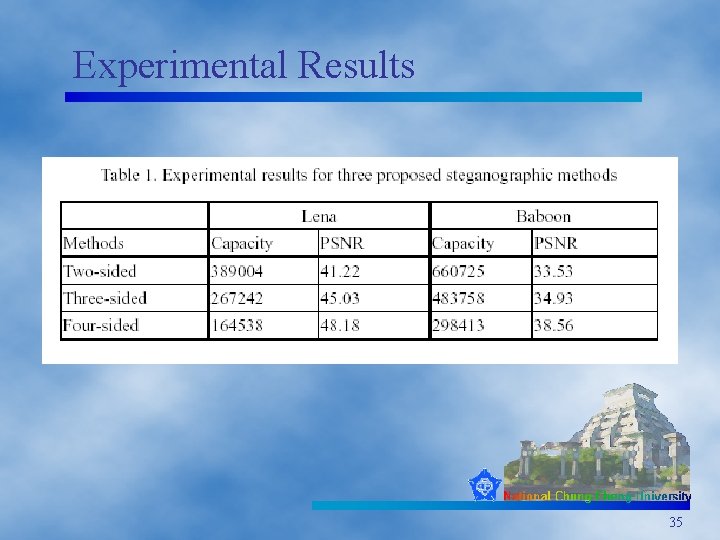
Experimental Results 35

Conclusions Provide large embedding capacity Without making noticeable distortion Pixels in edge areas may embed more data than those in non-edge areas No need of referencing original image when extracting 36