Hexadecimal GCSE Computer Science Hex Numbers Represent positive

Hexadecimal GCSE Computer Science

Hex Numbers Represent positive numbers in hexadecimal notation Click here for Topic Introduction

Hexadecimal Numbers A base is the number of digits in a number system. Once the denary digits have ‘run out’, hexadecimal makes use of letters Denary Hexadecimal 0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 A B C D E F

Use of Hexadecimal Show understanding of the reasons for choosing hexadecimal notation to represent numbers Identify current uses of hexadecimal numbers in computing, such as defining colours in Hypertext Markup Language (HTML), Media Access Control (MAC) addresses, assembly languages and machine code, debugging

Why use Hexadecimal? Fewer digits to represent larger numbers save space in output & make numbers easier to remember for humans. Humans use hexadecimal to represent longer numbers that would otherwise be difficult to remember. This does not save memory as when the data is converted to binary, it is no smaller.

Denary to Hexadecimal Convert positive hexadecimal integers to and from denary (a maximum of four hexadecimal digits will be required)

Hexadecimal 0 1 2 Denary to Hexadecimal is converted in nibbles (4 bits). Each nibble represents a single digit. 8 4 2 1 3 4 916 → 5 6 7 8 8 9 A 16 → A 8 0 4 1 2 0 1 1 B C 8 D 516 → 510 E F D 16 →

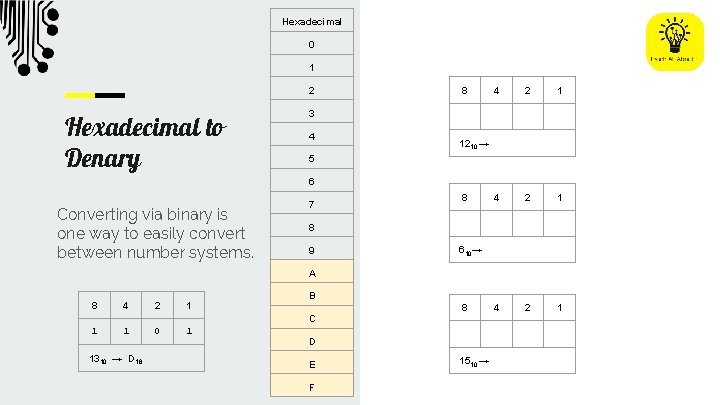
Hexadecimal 0 1 2 Hexadecimal to Denary Converting via binary is one way to easily convert between number systems. 8 4 2 1 3 4 1210 → 5 6 7 8 8 9 610→ A 8 4 2 1 B C 1 1 1310 → D 16 0 1 8 D E F 1510 →

Hexadecimal 0 1 2 Denary to Hexadecimal The alternative method of conversion requires integer division, but converts directly between the number systems. 3 4 5 6 Identify Denary 150 Divide by required Base 150 ÷ 16 = 9. 375 15 DIV 16 =9 15 MOD 16 0. 375 * 16 = 6 Convert to Hex 96 7 8 9 A B C D E F DIV - how many times does x go into y? MOD - what is the remainder after DIV?

Binary to Hexadecimal Convert positive hexadecimal integers to and from binary (a maximum of 16 bit binary numbers will be required)

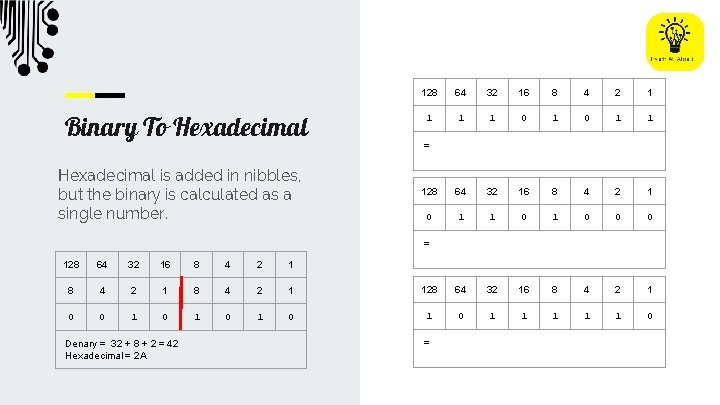
Binary To Hexadecimal is added in nibbles, but the binary is calculated as a single number. 128 64 32 16 8 4 2 1 1 0 1 1 128 64 32 16 8 4 2 1 0 1 0 0 0 = = 128 64 32 16 8 4 2 1 128 64 32 16 8 4 2 1 0 0 1 0 1 0 1 1 1 0 Denary = 32 + 8 + 2 = 42 Hexadecimal = 2 A =

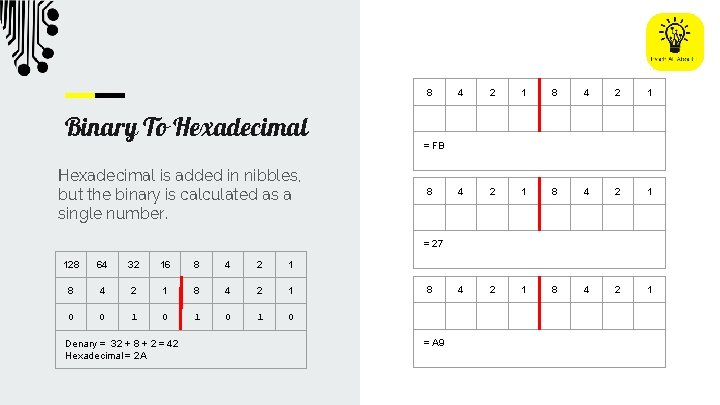
8 Binary To Hexadecimal is added in nibbles, but the binary is calculated as a single number. 4 2 1 8 4 2 1 = FB 8 = 27 128 64 32 16 8 4 2 1 0 0 1 0 1 0 Denary = 32 + 8 + 2 = 42 Hexadecimal = 2 A 8 = A 9

Exam Questions Represent positive numbers in hexadecimal notation Show understanding of the reasons for choosing hexadecimal notation to represent numbers Identify current uses of hexadecimal numbers in computing, such as defining colours in Hypertext Markup Language (HTML), Media Access Control (MAC) addresses, assembly languages and machine code, debugging Convert positive hexadecimal integers to and from denary (a maximum of four hexadecimal digits will be required) Convert positive hexadecimal integers to and from binary (a maximum of 16 bit binary numbers will be required)

Exam Question 1

Exam Question 2

Exam Question 3

Answers 8 4 15 = F FA 97 2 1 8 4 2 10 = A 1 8 4 2 9=9 1 8 4 2 7=7 1

Answers A binary bit pattern requires many more digits to represent a number. This means that it is easier for the programmer to read the hexadecimal.

Answers Although hexadecimal uses fewer digits to output the number, when it is converted to binary, it still uses the same amount of memory as it is the same binary number.