HEX red side blue side red player blue

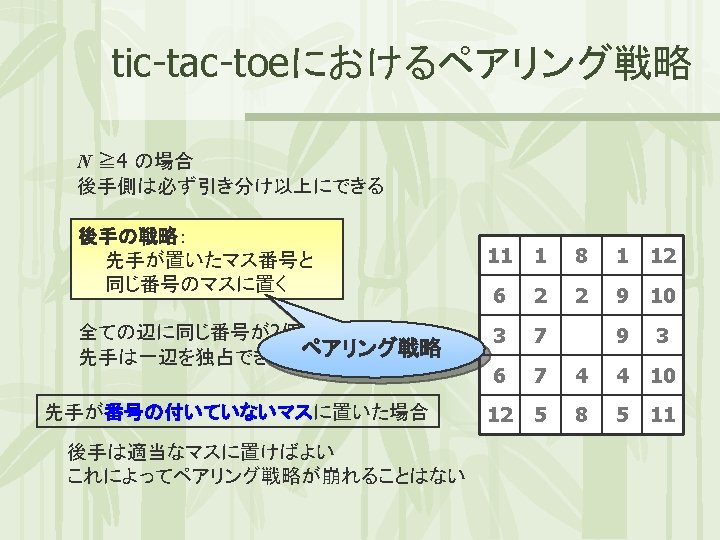
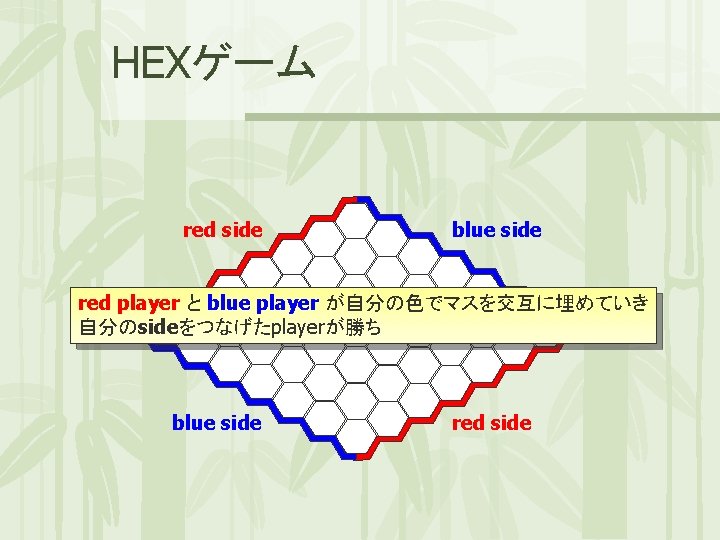
HEXゲーム red side blue side red player と blue player が自分の色でマスを交互に埋めていき 自分のsideをつなげたplayerが勝ち blue side red side

HEXゲーム red side blue side red side

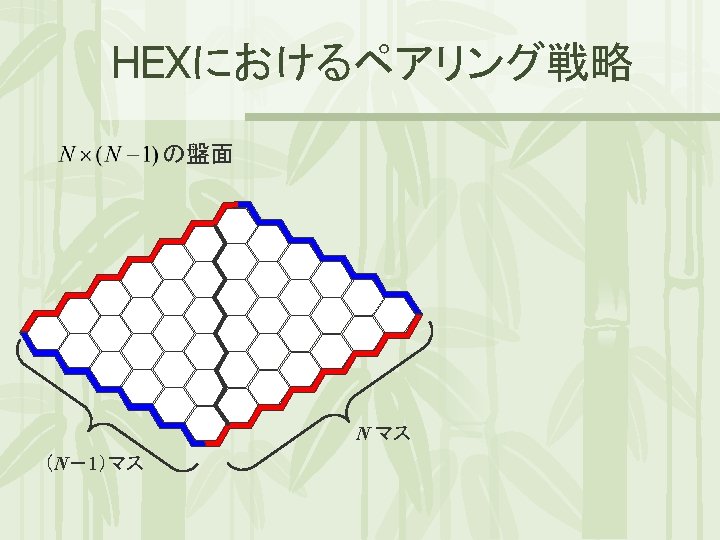
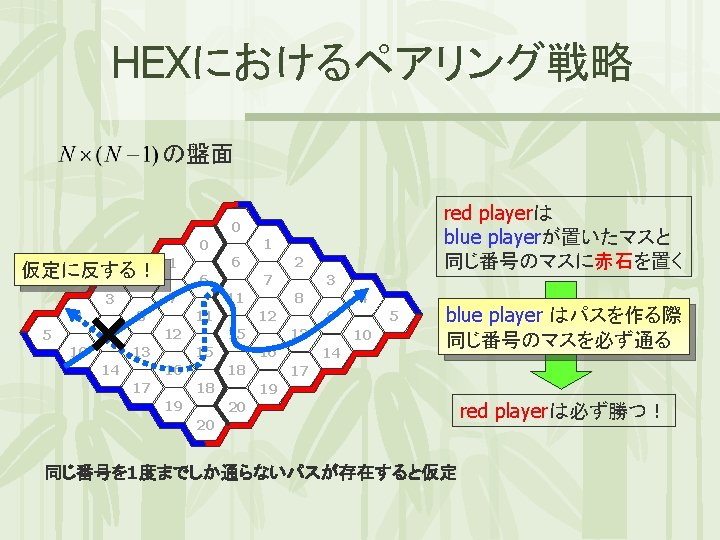
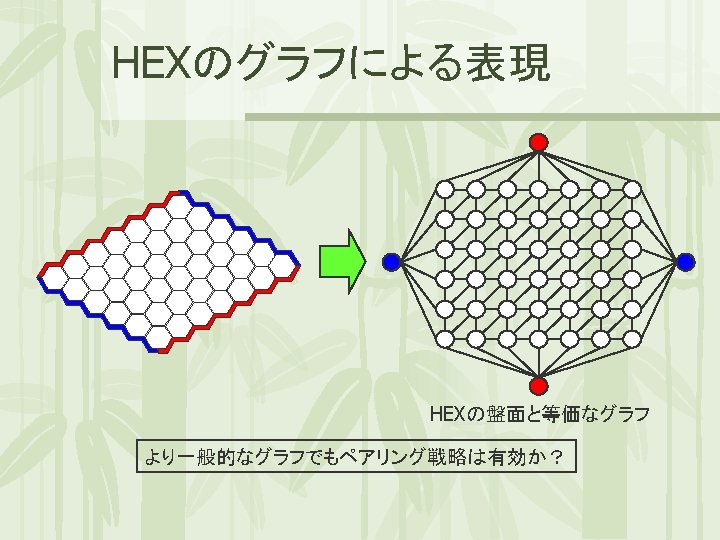
HEXにおけるペアリング戦略 の盤面 0 1 0 6 1 6 2 7 3 8 4 9 5 10 11 12 14 12 15 17 5 9 16 18 4 13 18 19 3 8 15 16 10 14 17 19 20 20 （N－1）マス 7 11 13 2 N マス

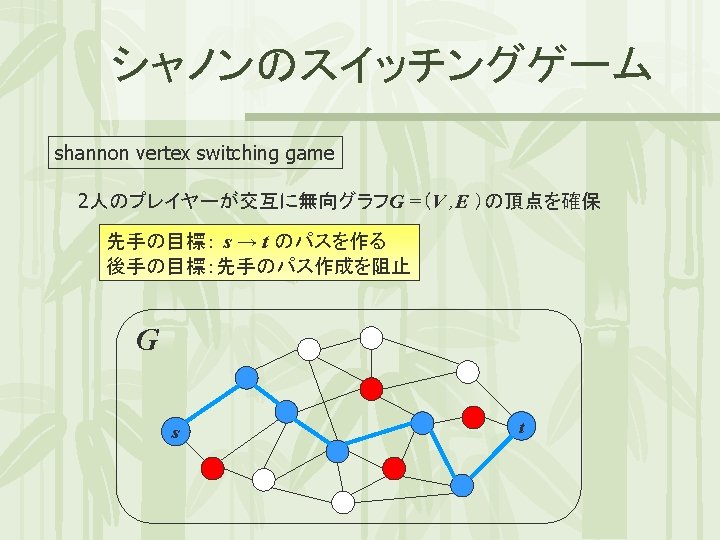
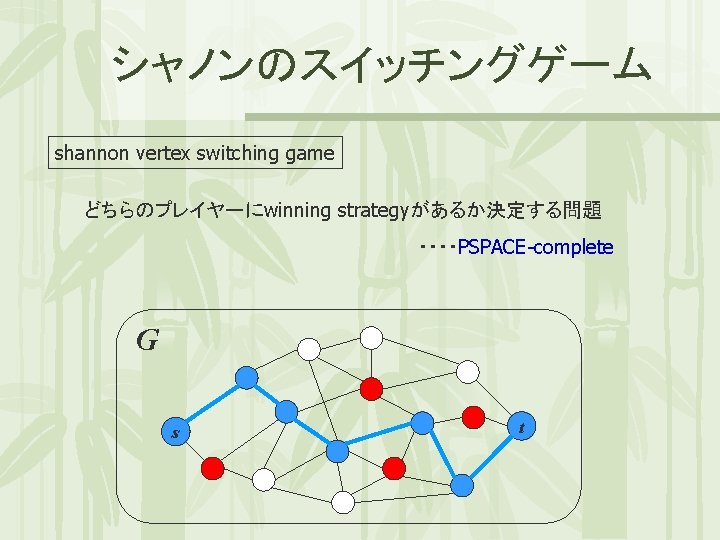
シャノンのスイッチングゲーム shannon vertex switching game どちらのプレイヤーにwinning strategyがあるか決定する問題 ・・・・PSPACE-complete G s t

PERFECT-FP問題 後手の戦略 に対応 次のような問題を考える PERFECT-FP ={(G, s, t ) | G has perfect forbidden pairs} ただし G = (V, E) ，始点をs，終点をt とする 先手の戦略 に対応 PATH-WITH-FP ={(G, s, t, P ) | G has a path from s to t that contains at most one vertex from each pair in P} ただし P = { (p 1, q 1) , ･･･, (pk , qk) } (1≦k与えられた禁止対の割当てが ≦ ), pi , qi ∈V (1≦i≦k) とする perfect forbidden pairs でな いかどうか

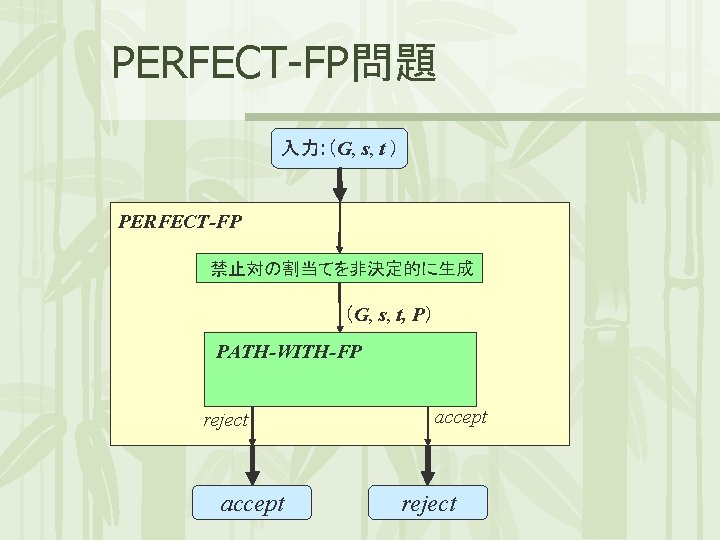
PERFECT-FP問題 入力: （G, s, t ） PERFECT-FP 禁止対の割当てを非決定的に生成 （G, s, t, P） PATH-WITH-FP reject accept reject

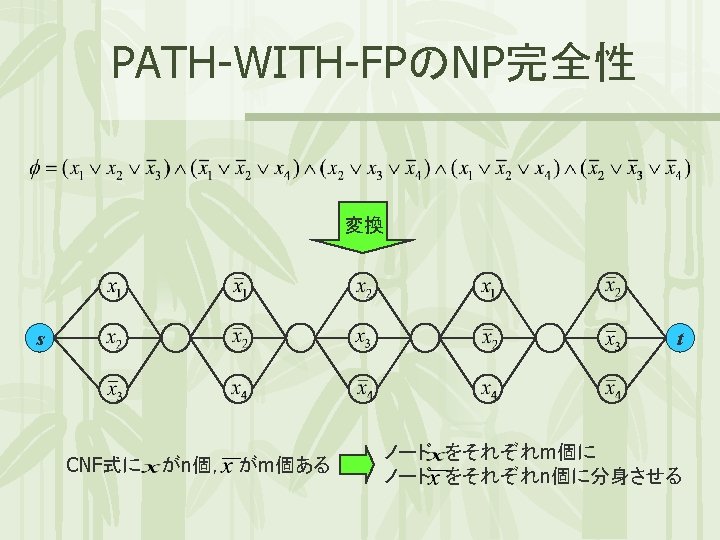
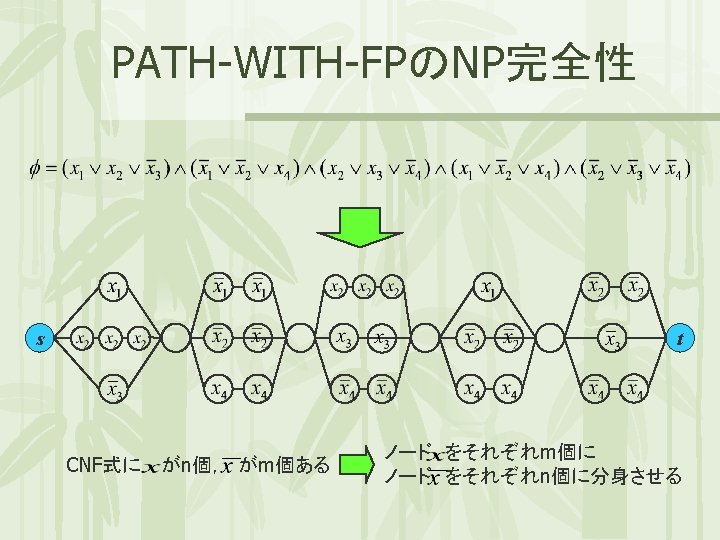
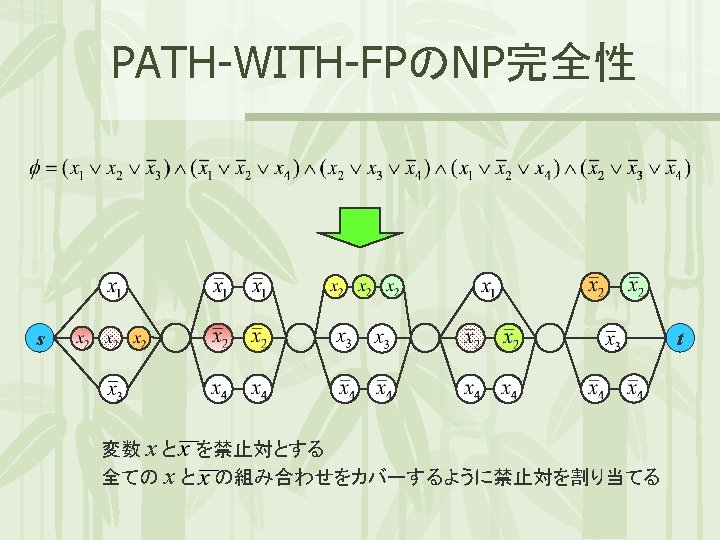
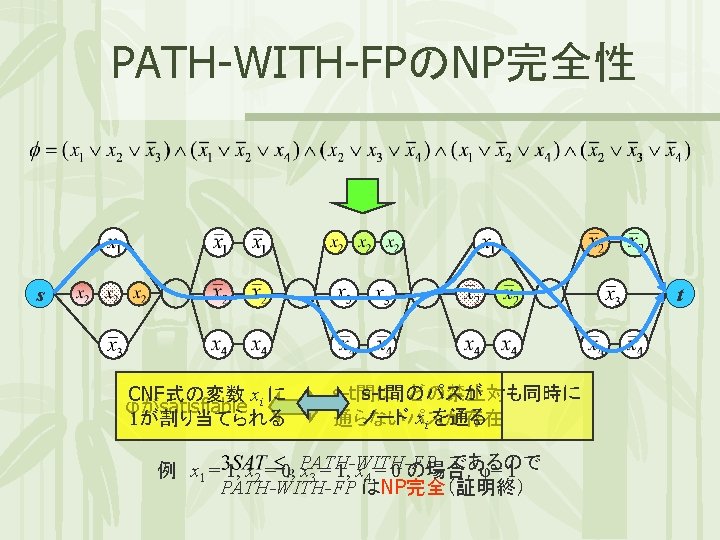
PATH-WITH-FPのNP完全性 定理： PATH-WITH-FP はNP完全である ［HAROLDら，1976］ ２．『PATH-WITH-FP はNP-hard 』 の証明 3 SAT から PATH-WITH-FP へ帰着

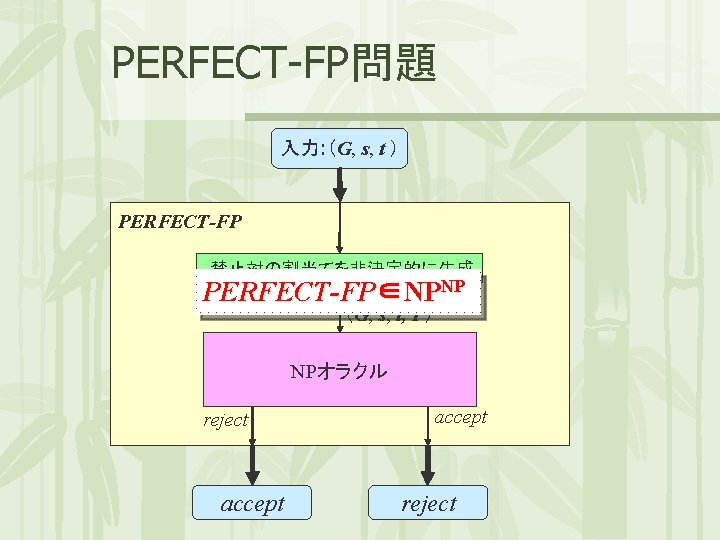
PERFECT-FP問題 入力: （G, s, t ） PERFECT-FP 禁止対の割当てを非決定的に生成 PERFECT-FP∈NPNP （G, s, t, P） PATH-WITH-FP NPオラクル reject accept reject