Heuristics for Minimum Brauer Chain Problem Fatih Gelgi

Heuristics for Minimum Brauer Chain Problem Fatih Gelgi Melih Onus

Outline n n n Problem Definition Binary Method Factor Method Heuristics Experimental Results Conclusions

Brauer Chain A Brauer chain for a positive integer n is a sequence of integers 1 = a 0, a 1, a 2, …, ar = n such that ai = ai-1 + ak for some 0 ≤ k < i and 1 ≤ i ≤ n n Example: 1 1, 1+1=2 1, 2, 2+2=4 1, 2, 4, 4+2=6 1, 2, 4, 6, 6+6=12 1, 2, 4, 6, 12+2=14 is a Brauer chain for 14 with length 5 n

Binary Method Write the number n in binary form n Replace each 1 with DA and each 0 with D n Remove the leading DA n Begin from 1, follow the sequence from left to right n – For each D, double the current number – For each A, add 1 to the current number n Example: – Binary representation of 19 is 10011 – Sequence is DDDADA – 1, 1+1=2, 2+2=4, 4+4=8, 8+1=9, 9+9=18, 18+1=19

Factor Method n n n Let n = p*q where n, p, q Z+. First calculate Brauer chain for p and q Let 1 = a 1, a 2, …, ak = p is Brauer Chain for p Let 1 = b 1, b 2, …, bk = q is Brauer Chain for q 1 = a 1, a 2, …, ak = p*b 1, p*b 2, …, p*bm = p*q is a Brauer chain for n=p*q Example: – <1, 2 , 4, 5> <1, 2, 3> – <1, 2 , 4, 5, 10, 15>

Heuristics Binary Heuristic n Factorization Heuristic n Dynamic Heuristic: n – It uses the previous solutions to obtain the best solution for current n value – We store only one solution for each number – The dynamic formula is, l(n) = min{l(k)+1} where k<n and the solution sequence of k must contain n-k n 2 -3 -5 Heuristic – This algorithm always begins with numbers 1, 2, 3, 5, …. – For the next element, it selects as maximum as possible 2 -3 -6 Heuristic n 2 -4 -8 Heuristic n

Experiments We did 3 types of experiments – We calculated all n values up to about 4500 – We calculated only one randomly chosen n value within each interval of 200 up to 10000 – We calculated all n values up to 20000 (using factorization and dynamic heuristics) n To calculate optimum value, we used exhaustive search with branch and bound technique n Although our pruning conditions make the search quite faster, we were able to calculate the optimum values up to 4500 since the running time is O(n!) n

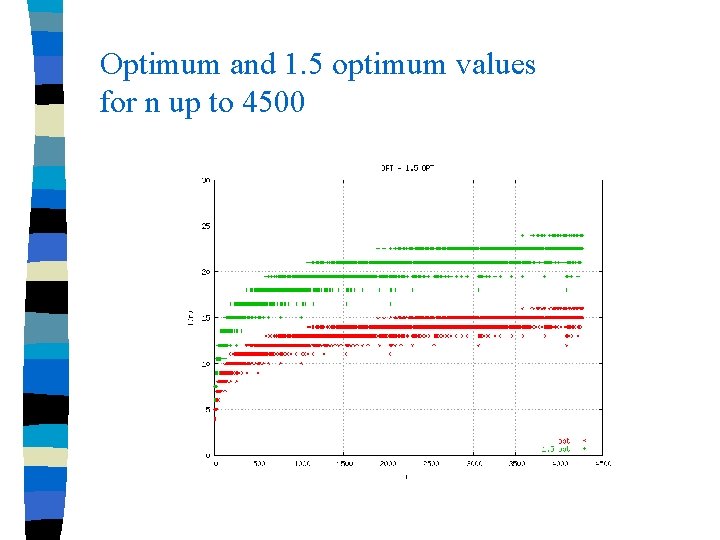
Optimum and 1. 5 optimum values for n up to 4500

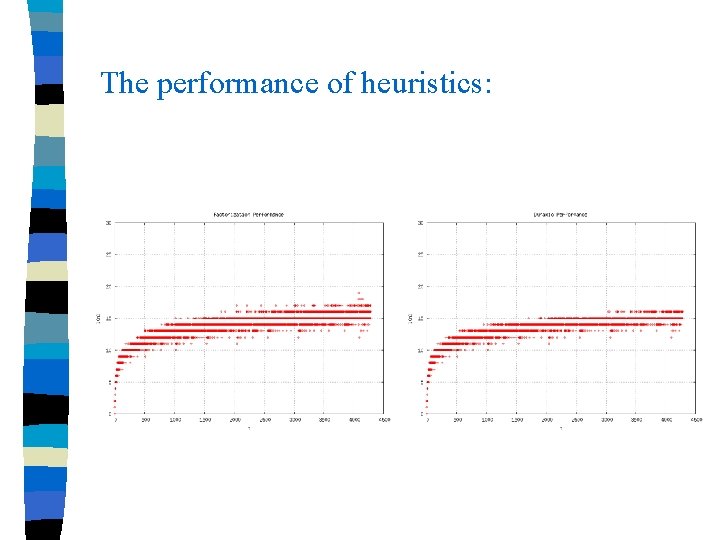
The performance of heuristics:

Experiment II To obtain optimum values for larger n’s and increase the quality of our experiments, for each interval with size 200 we chose a random n value n All the solutions of heuristics are clearly smaller than 1. 5 optimum n

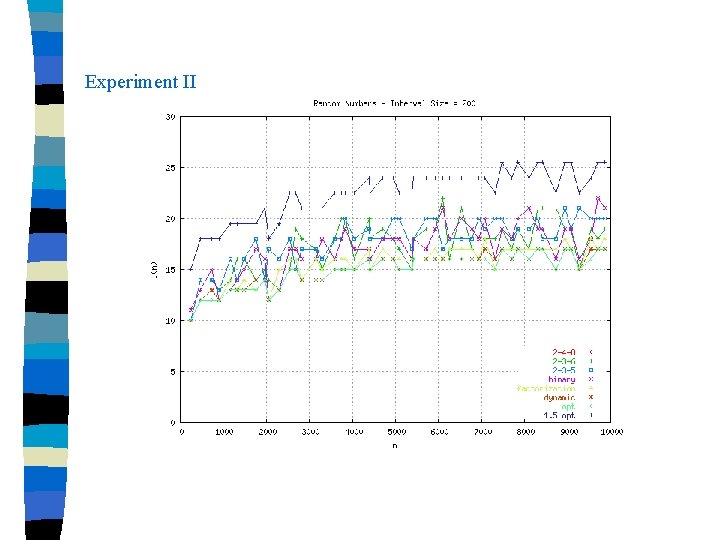
Experiment II

Approximation Ratios All the heuristics obviously has 1. 5 approximation ratios n Better than 2 -4 -8, 2 -3 -6, 2 -3 -5 and binary, factorization has 1. 25 approximation value n Dynamic has an incredible approximation ratio with 1. 1 n Empirically, factorization is even smaller than 1. 5 lg n and dynamic is smaller than 1. 4 lg n n

Conclusion n n n Several heuristics for approximating minimum Brauer chain problem is discussed The optimum function is not monotone we couldn’t prove a theoretical approximation ratio better than 2 Experimental results show that there is empirically an approximation with 1. 1 which is incredible for the problem For approximation results, we also achieved 1. 4 lg n length for any number n where the trivial lower bound is lg n Providing a better lower bound, the approximation factor can be decreased With a good lower bound, approximation factor can be proved theoretically